简单线性变换
平移、旋转和镜像变换
平移变换
矩阵形式：
\[\begin{pmatrix} x^\prime\\y^\prime\\z^\prime \end{pmatrix}=\begin{pmatrix} x\\y\\z \end{pmatrix}+\begin{pmatrix} a\\b\\c \end{pmatrix}
\]
向量在加上是特殊的矩阵。
旋转变换
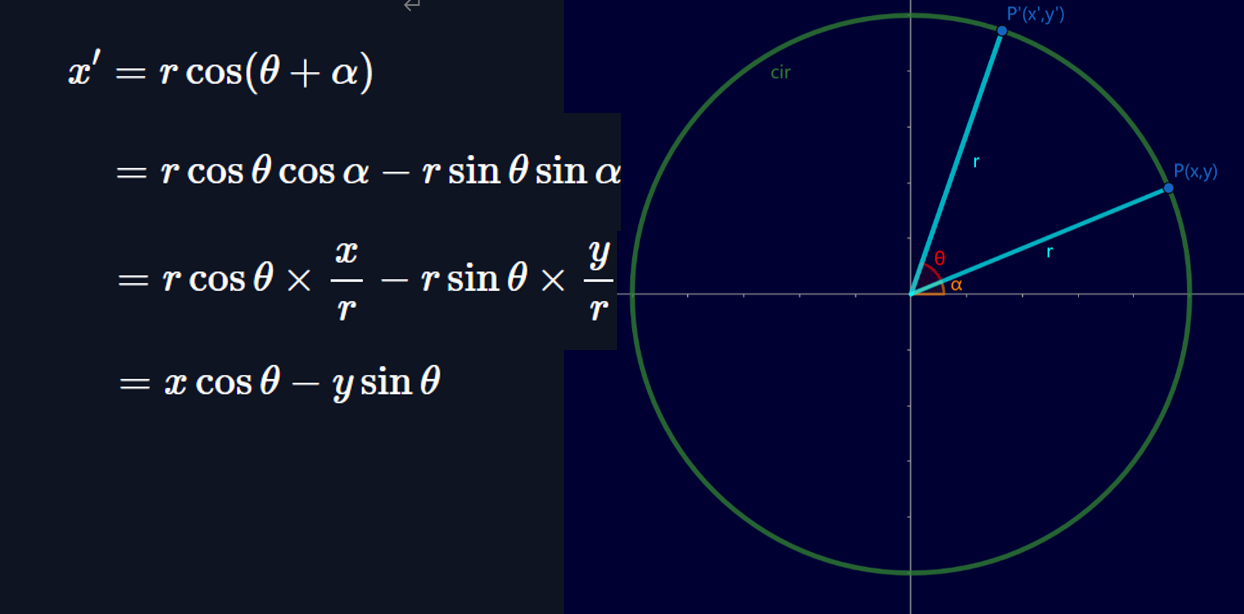
定义：点 \(P(x,y)\) 绕原点逆时针旋转 \(\theta\) 后得点 \(P^\prime(x^\prime,y^\prime)\)。
转换公式：\(x^\prime= x \cos \theta - y \sin \theta, y^\prime= x \sin \theta + y \cos \theta\)
写成矩阵形式即：
\[\begin{pmatrix} x^\prime\\y^\prime \end{pmatrix}=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}
\]
证明：以 \(x^\prime\) 变换式为例：
镜像变换
定义： 点 \(P(x,y)\) 对于过原点的直线 \(y= \tan \frac{\theta}{2} · x\) 对称至点 \(P^\prime(x^\prime,y^\prime)\)。
转换公式： \(x^\prime= x \cos \theta + y \sin \theta, y^\prime= x \sin \theta - y \cos \theta\)
写成矩阵形式即：
\[\begin{pmatrix} x^\prime\\y^\prime \end{pmatrix}=\begin{pmatrix} \cos \theta & \sin \theta \\ \sin\theta & -\cos\theta \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}
\]
证明：以 \(x^\prime\) 变换式为例
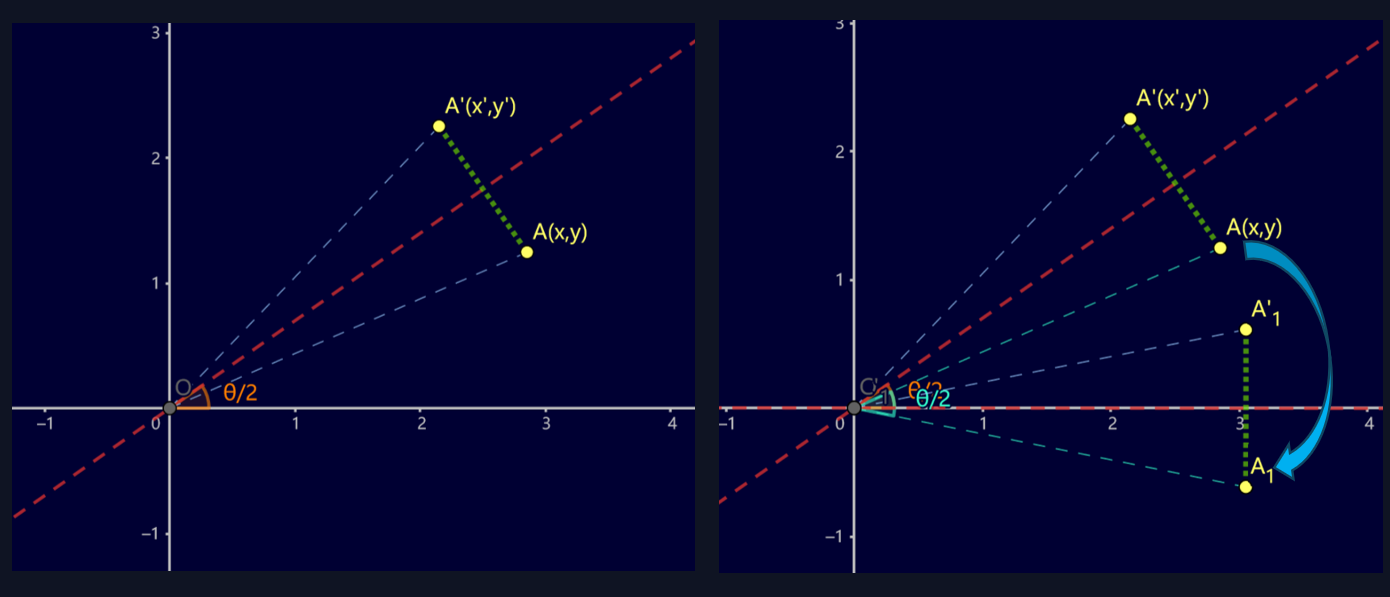
将 \(A,A^\prime\) 两点顺时针旋转 \(\frac{\theta}{2}\) 得 \(A_1,A_1^\prime\)。如此以来，旋转后的两点 \(A_1,A_1^\prime\) 关于 \(x\) 轴对称，容易列出方程：
\[\begin{cases} x(A_1)=x(A_1^\prime) \\ y(A_1)=-y(A_1^\prime) \end{cases}
\]
即，
\[\begin{cases} x \cos \frac{\theta}{2} + y \sin \frac{\theta}{2} = x^\prime \cos \frac{\theta}{2} + y^\prime \sin \frac{\theta}{2} \\ x \sin \frac{\theta}{2} - y \cos \frac{\theta}{2} = - x^\prime \sin \frac{\theta}{2} +y^\prime \cos \frac{\theta}{2}\end{cases}
\]
将一式等号两侧同乘 \(\cos \frac{\theta}{2}\)，二式等号两侧同乘 \(\sin \frac{\theta}{2}\) 得：
\[\begin{cases} x \cos^2 \frac{\theta}{2} + y \sin \frac{\theta}{2} \cos \frac{\theta}{2} = x^\prime \cos^2 \frac{\theta}{2} + y^\prime \sin \frac{\theta}{2} \cos \frac{\theta}{2} \\ x \sin^2 \frac{\theta}{2} - y \sin \frac{\theta}{2} \cos \frac{\theta}{2} = - x^\prime \sin^2 \frac{\theta}{2} +y^\prime \sin \frac{\theta}{2}\cos \frac{\theta}{2}\end{cases}
\]
上式减下式，得：
\[x(\cos^2 \frac{\theta}{2} - \sin^2 \frac{\theta}{2}) +2y \sin \frac{\theta}{2} \cos \frac{\theta}{2}= x^\prime(\cos^2 \frac{\theta}{2} + \sin^2 \frac{\theta}{2})
\]
化简得：$x \cos \theta + y \sin \theta = x^\prime $
\(\Box\)
