[安乐椅#13] 泰勒展开 & 帕德逼近 & 洛朗级数

泰勒展开

$f(x)$ 在 $x=x_0$ 处的泰勒展开：

$$f(x)\thickapprox \sum \dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n,x\ge x_0$$

取 $x_0=0$，即得出 $f(x)$ 的麦克劳林展开：

$$f(x)\thickapprox \sum \dfrac{f^{(n)}(0)}{n!}x^n,x\ge 0$$

即

$$f(x)\thickapprox f(0)+f^\prime (0)x+\dfrac{f^{\prime\prime}(0)}{2}x^2+\cdots+\dfrac{f^{(n)}(0)}{n!}x^n,x \ge x_0$$

---

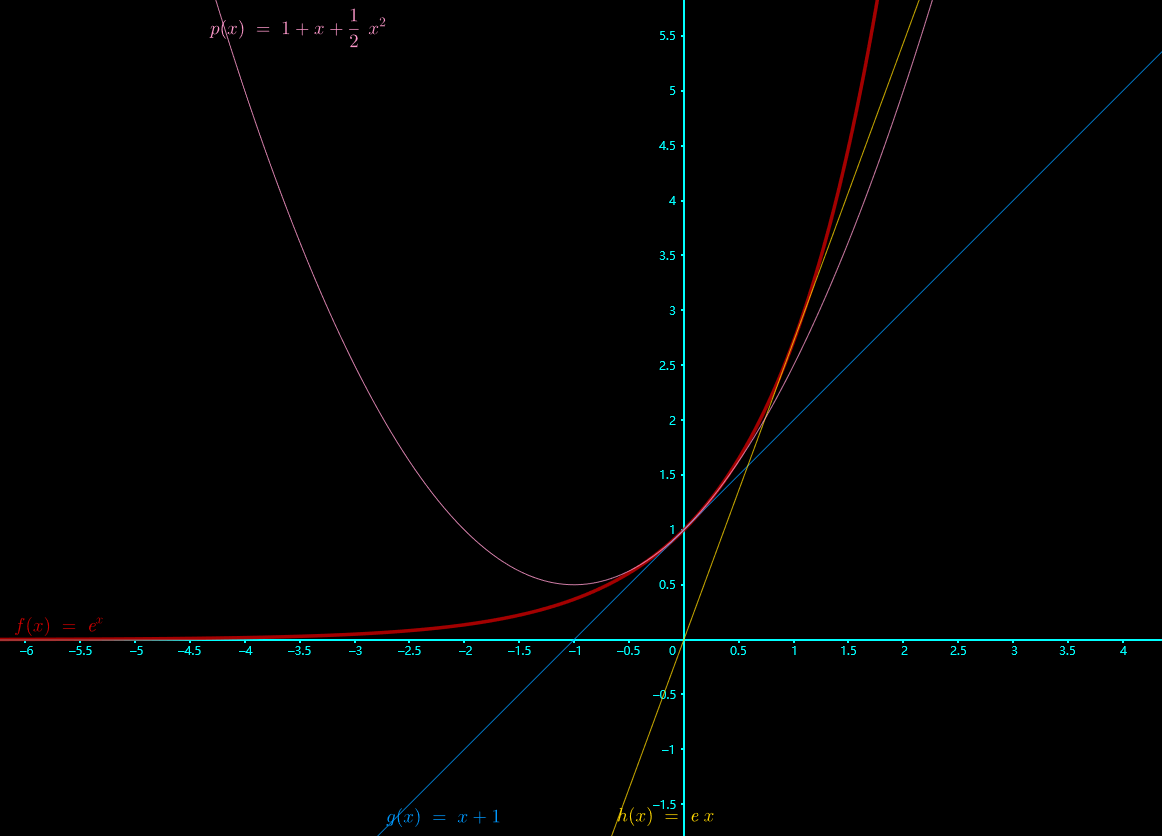
泰勒展开拟合指数函数可以取得不错的效果。以 $f(x)=e^x$ 为例，泰勒展开可指引包括但不限于以下经典的函数放缩：

• $e^x \ge x+1$

• $e^x \ge ex$

• $e^x \ge 1+x+\frac{1}{2}x^2,x \ge 0$

---

帕德逼近

泰勒展开拟合指数函数很理想，但拟合对数函数时就不够理想：

可以看到，泰勒展开拟合对数函数时往往在某一“前缀”中比较合适，在这之后就直接飞掉了。

---

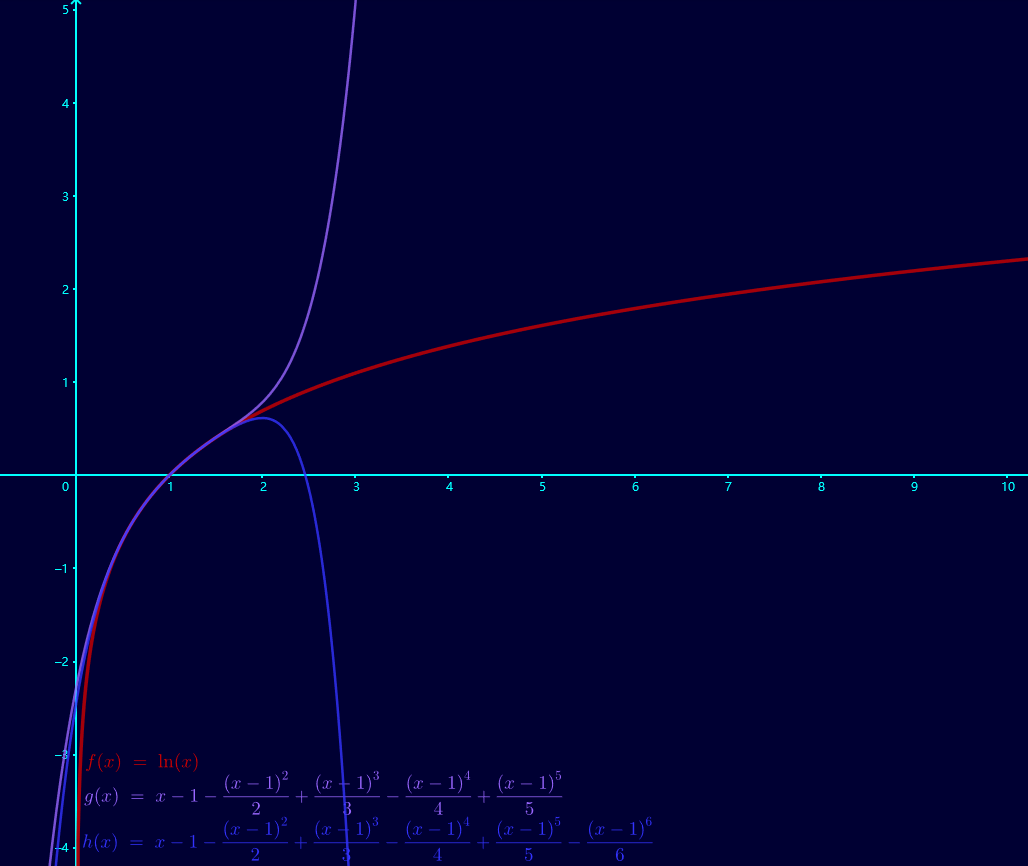
泰勒展开是利用多项式函数去拟合，其不可避免的是随多项式函数的次数增高，在 $x \rightarrow + \infty$ 时，函数值会很快地趋向于无穷。而对数函数在 $x \rightarrow + \infty$ 时，函数值趋向于无穷的趋势很慢。故泰勒展开并不适合与拟合对数函数。

分式函数可以解决这个问题，而帕德逼近的基本形式就是分式函数:

$$f(x) \thickapprox \dfrac{b_mx^m+\cdots+b_1x^1+b_0}{a_nx^n+\cdots+a_1x^1+a_0}$$

逼近思路类似于泰勒展开。求这样一个分式函数，使得其的 $n$ 阶导均和 $f(x)$ 的 $n$ 阶导相同，即称该分式函数为 $f(x)$ 的一个帕德逼近。

但是求解过程及其难算$^*$，一般需要借助机子。所以直接把结论记住就好了。

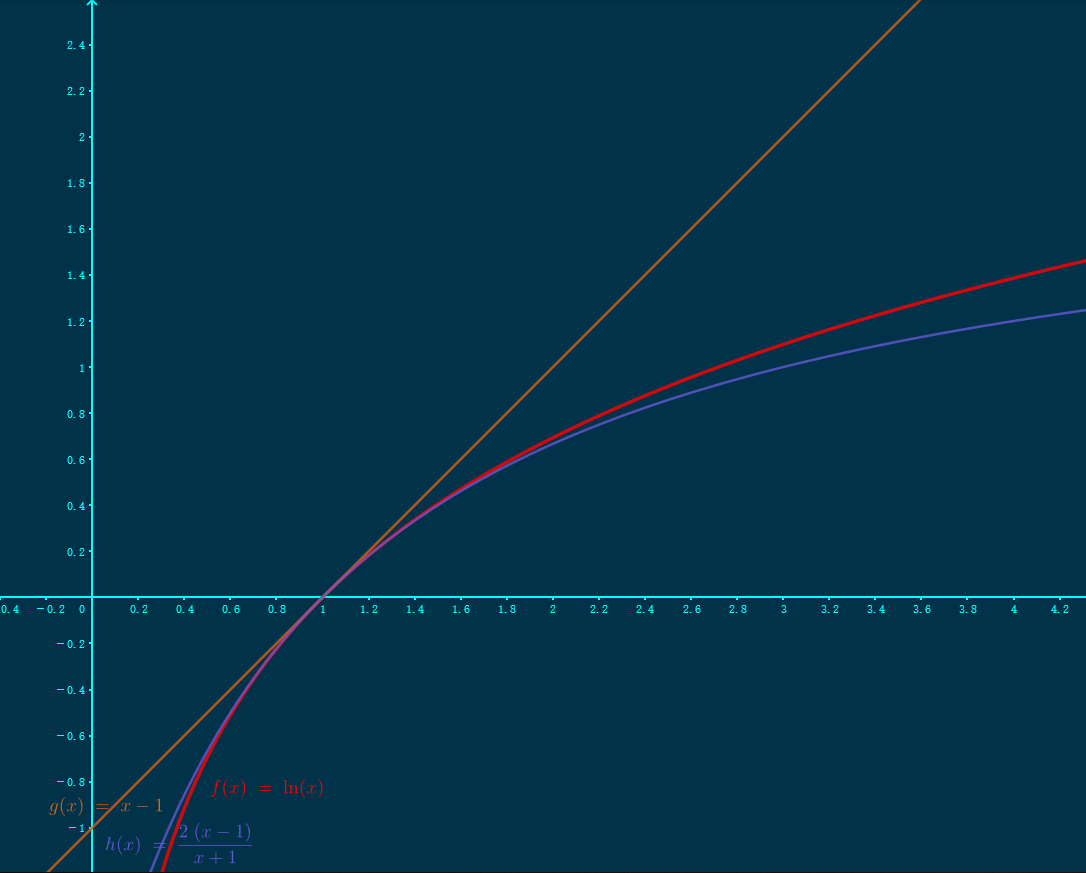
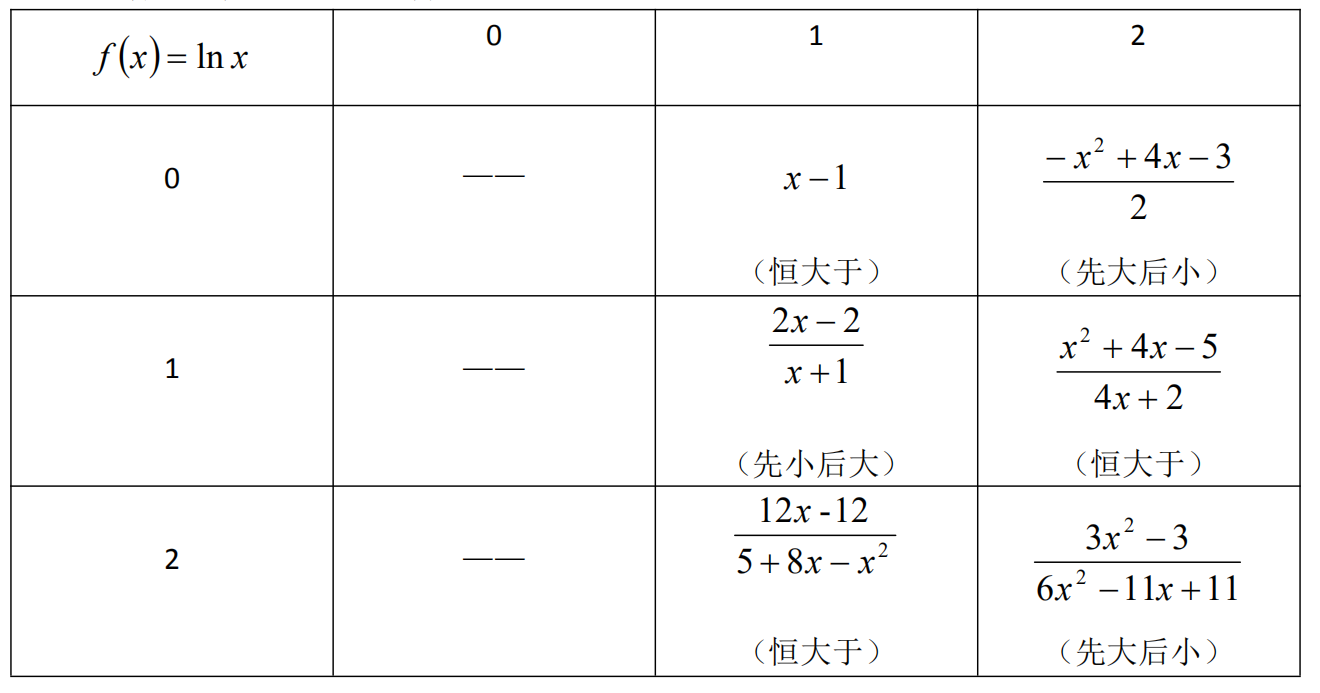(大小关系改变点均为 $x=1$)

---

洛朗级数

实洛朗级数。$^*$

精度更高，但更不会求解了。直接记结论：

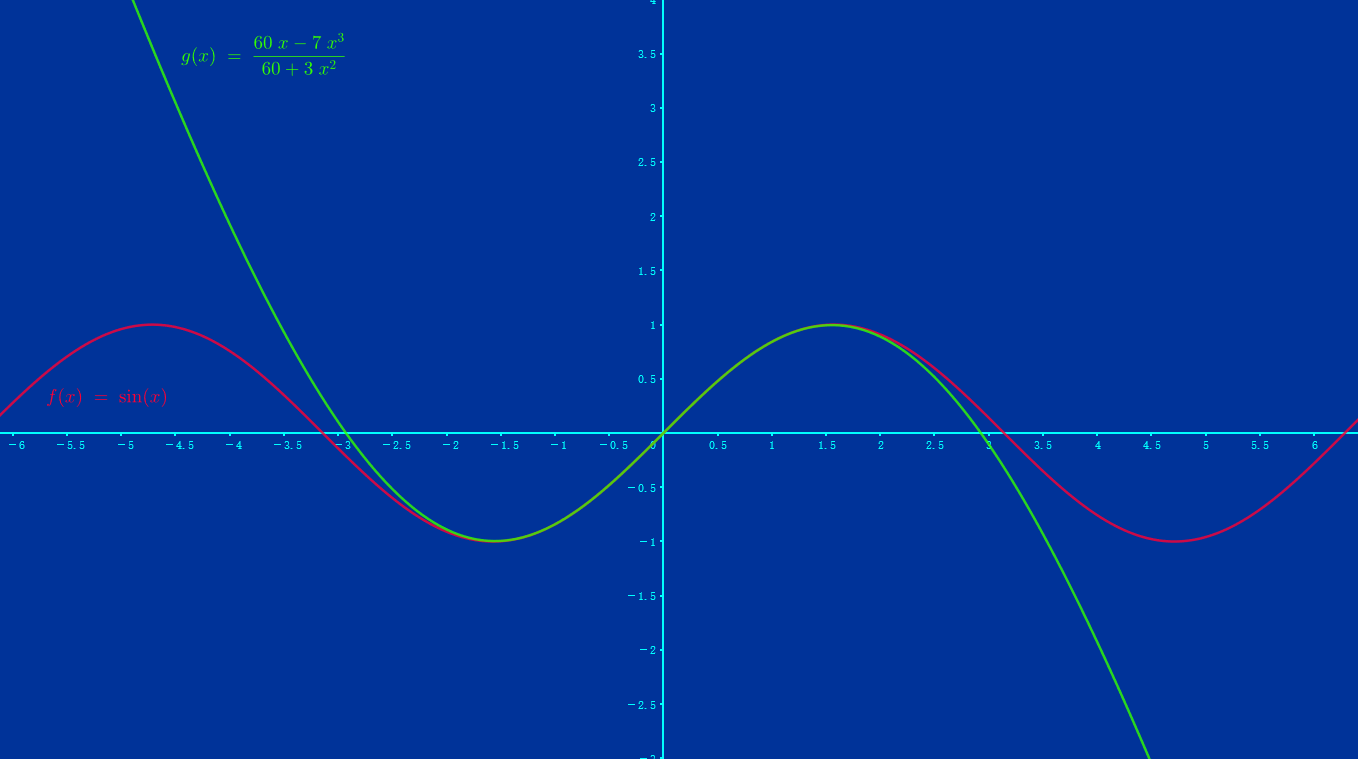
• $\sin x \ge \dfrac{60x-7x^3}{60+3x^2},x\ge 0$

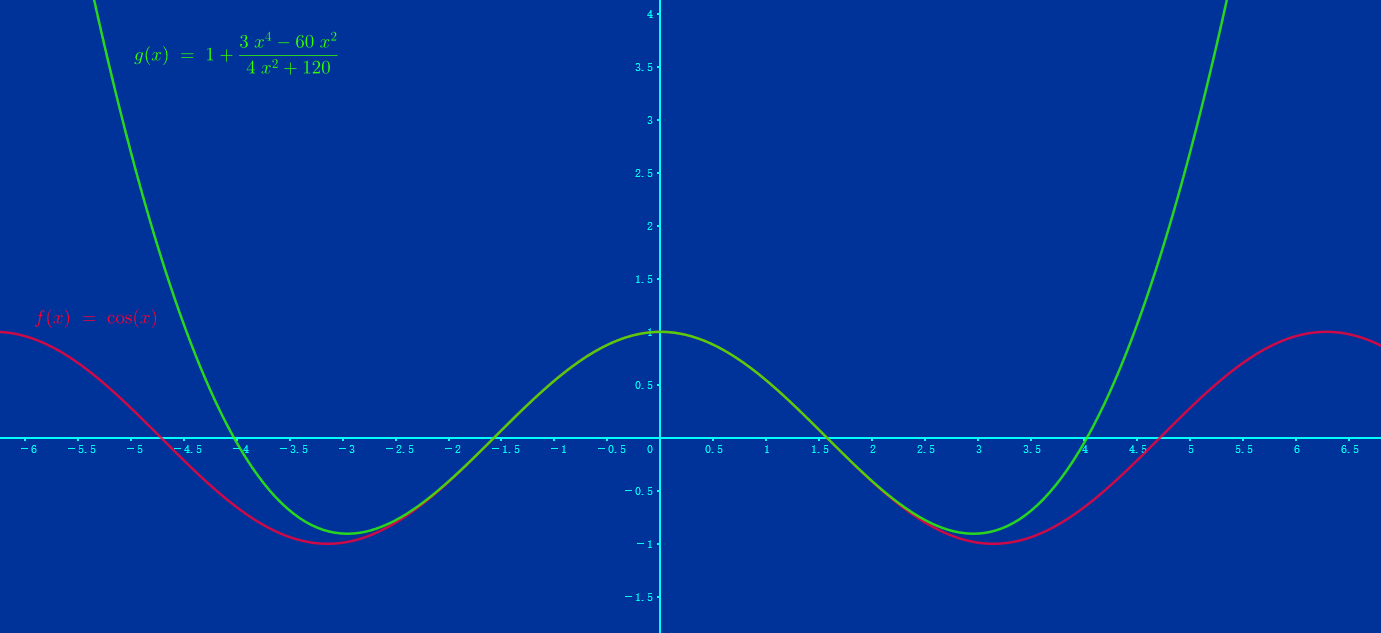
• $\cos x \le 1+\dfrac{3x^4-60x^2}{4x^2+120},x \in \mathbb{R}$