会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
SigmaToT
博客园
首页
新随笔
联系
订阅
管理
上一页
1
2
3
4
5
6
···
10
下一页
2025年10月30日
洛必达法则
摘要: 我最爱的洛小姐!!!😍 洛必达法则:若 \(f(x)\) 在 \(a\) 的某一去心邻域内可导,\(g(x)\) 在 \(a\) 的某一去心邻域内可导,且 \(f(a)= 0,g(a) = 0\) 或 \(f(a) = \infty/\!-\! \infty,g(a) = \infty/\!-\!
阅读全文
posted @ 2025-10-30 23:09 SigmaToT
阅读(21)
评论(0)
推荐(0)
2025年10月27日
极值定理
摘要: 若函数 \(f\) 在 \(x = c\) 处有一个局部最大值或局部最小值,则 \(f\) 在 \(x = c\) 处不可导或者 \(f'(c)=0\) 。 比如说 \(f\) 在 \(x = c\) 处是个尖角,那么肯定就不可导。 若可导,不妨令是最大值(最小值类似)则说明 \[\lim_{h\t
阅读全文
posted @ 2025-10-27 20:09 SigmaToT
阅读(21)
评论(0)
推荐(0)
2025年10月25日
一个关于cos的极限
摘要: \[\lim_{x\to 0}\dfrac{1 - \cos x}{x} = 0 \]第一种推导方法:使用勾股定理。 \[\begin{align*} \lim_{x\to 0}\dfrac{1 - \cos x}{x} &= \lim_{x\to 0}\dfrac{1 - \cos x}{x}\c
阅读全文
posted @ 2025-10-25 12:59 SigmaToT
阅读(39)
评论(0)
推荐(0)
三角函数的2倍角公式
摘要: 根据 \(\cos(x + y) = \cos x\cos y - \sin x\sin y\) 和 \(\sin(x + y) = \sin x\cos y + \cos x\sin y\)(具体看这里)。 我们可以得到 \(\cos 2x = \cos(x + x) = \cos^2x - \s
阅读全文
posted @ 2025-10-25 12:38 SigmaToT
阅读(91)
评论(0)
推荐(0)
2025年10月24日
一个关于sin的极限
摘要: \[\lim_{x\to 0} \dfrac{\sin x}{x} = 1 \]因为 \(y = \sin x\) 关于坐标轴原点中心对称,所以我们只需要证明 \[\lim_{x\to 0^+}\dfrac{\sin x}{x} = 1 \]就行。 我们先规定, \(0 < x < \dfrac{\
阅读全文
posted @ 2025-10-24 23:41 SigmaToT
阅读(37)
评论(0)
推荐(0)
关于cos(x + y)和sin(x + y)的公式的几何证明
摘要: 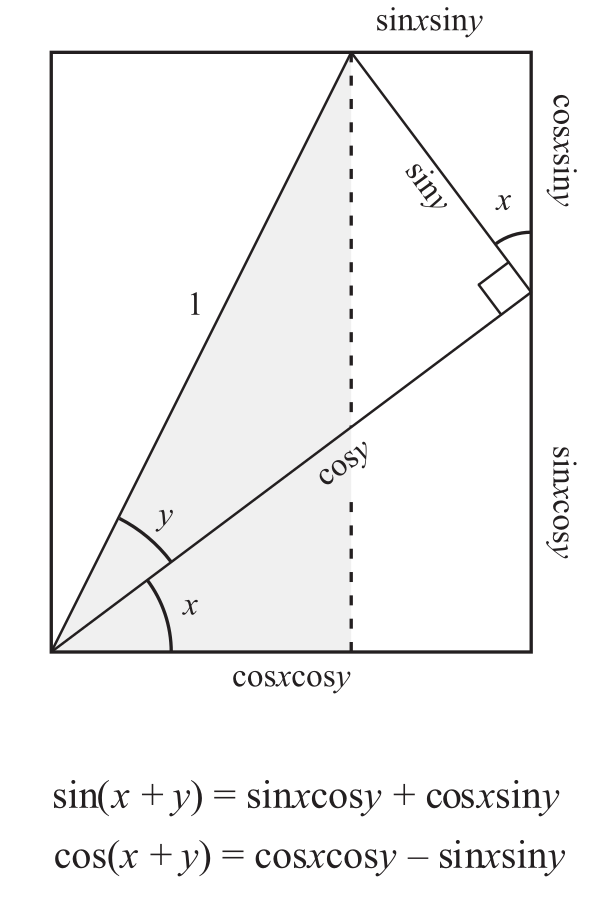
阅读全文
posted @ 2025-10-24 22:54 SigmaToT
阅读(62)
评论(0)
推荐(0)
2025年10月22日
幂是任意常数的二项式定理
摘要: 我们引入 \((1 + t)^n,n\in\mathbb{R}\) 这个东西。 若 \(t = -1\),当 \(n\leq 0\) 时,这个东西没有意义,否则他是 \(0\)。 若 \(t = 1\),我们显然不用展开了。 若 \(|t| < 1\) 时。 我们使用麦克劳林公式(泰勒展开的 \(x
阅读全文
posted @ 2025-10-22 23:23 SigmaToT
阅读(18)
评论(0)
推荐(0)
2025年10月21日
一些微积分中的中值定理
摘要: 积分第一中值定理: 设 \(f(x)\) 在 \([a, b]\) 连续,且 \(g(x)\) 在 \([a,b]\) 可积且不变号(始终非负或始终非负),那么存在 \(c\in [a,b]\),使得 \[\int^b_af(x)g(x)\text{d}x = f(c)\int^b_ag(x)\te
阅读全文
posted @ 2025-10-21 23:00 SigmaToT
阅读(51)
评论(0)
推荐(0)
泰勒展开
摘要: 假设 \(f(x)\) 有 \(N\) 阶导。 \(x_0\) 可以是随便一个值,使得 \(f(x)\) 的任意阶导数在此有定义。 \[f(x) = f(x_0) + \int^x_{x_0}f'(t)\text{d}t \]然后我们换一下积分变量。 \[f(x) = f(x_0) + \int^x
阅读全文
posted @ 2025-10-21 22:29 SigmaToT
阅读(39)
评论(0)
推荐(0)
2025年10月13日
正睿25csp七连测day5
摘要: 题面: 这场打得很飞舞,\(40pts,rk54\)。 T1 这道题比较考验思维。 我们可以考虑每个点是从最初序列的哪个位置转移过来了(记为 \(from\))。 不难发现,如果最终序列中的几个位置的 \(from\) 相等,那么这几个位置代表的数的和肯定模 \(10\) 同余于 \(from\)
阅读全文
posted @ 2025-10-13 22:10 SigmaToT
阅读(15)
评论(0)
推荐(0)
上一页
1
2
3
4
5
6
···
10
下一页
公告