正睿25noip十连测day5

题面：

今天有点 fvv，只是 \(110pts,rk124\)。

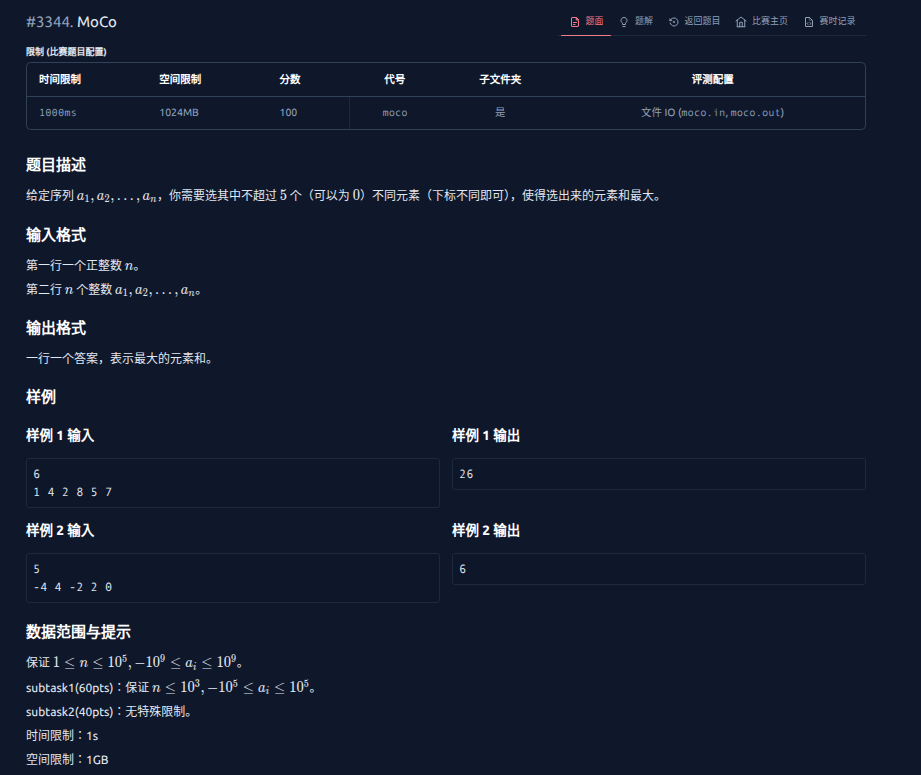
T1

这道题是签到题，显然不用说。

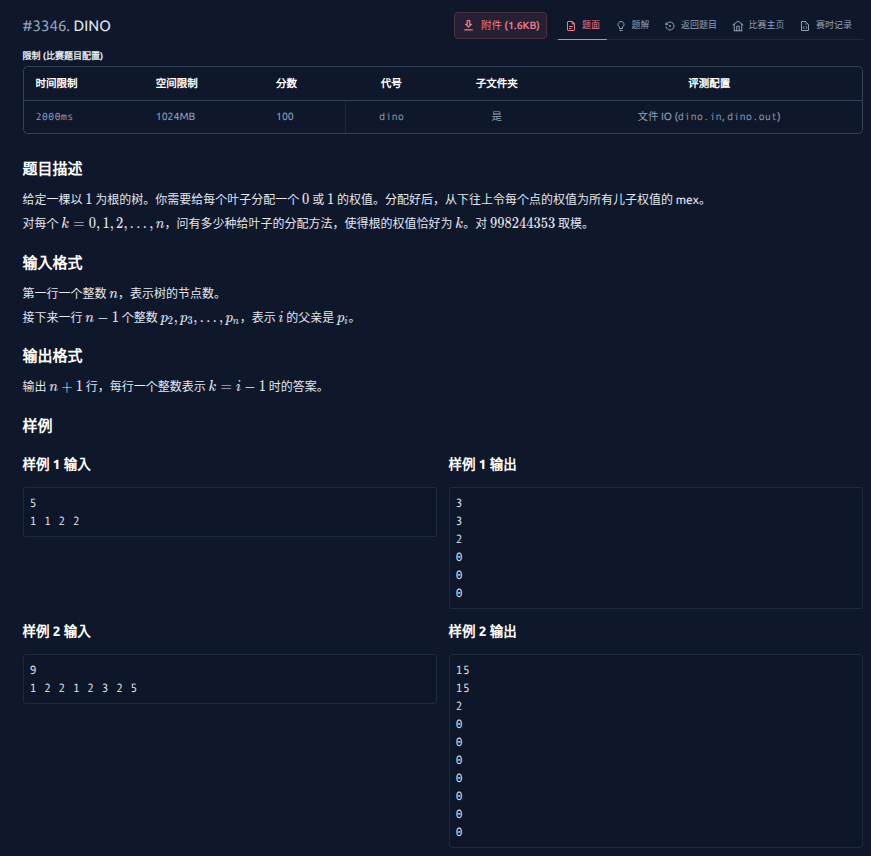
T2

这道题比较难想。
我们先考虑这个给的数据范围啥意思。
\(2e5\) 大概率是 \(\mathcal{O}(n)\) 或 \(\mathcal{O}(n\log n)\)。
然后到了 noip 这个级别，如果是 \(\mathcal{O}(n)\) 的话，一般就给你 \(1e6\) 了。

然后这种计数题一般是 \(dp\)，所以我们考虑 \(dp\) 的状态能是啥。

首先肯定有个 统计到 x 这个点，所以我们就考虑第二维是啥。

第二个变化并且题目里面提到的量显然是当前节点的 \(mex\)。

因此，我们就维护每个点的 \(mex\)。

但是直接维护显然不好维护，我们需要状压一下。

然而 \(1e5\) 显然太大了，不可行。

我们考虑每个如果 \(mex\) 是 \(k\)，那么对它的子节点有什么要求。

我们发现如果要构造出一个点的 \(mex\) 是 \(k\)，那么需要的节点数

\[f(k) = \begin{cases} 1&,k = 0\\ 1 + \displaystyle\sum_{j = 0}^{k - 1}f(j)&,k > 0 \end{cases} \]

因为这要求这个点的所有子节点分别 \(mex\) 是 \(0\sim k - 1\)。

因此 \(f(k) = 2^{k}\)。

简单证明一下：

我们考虑数学归纳法。

首先，当 \(k = 0\) 时，显然成立。

当 \(k > 0\) 时，我们不妨令 \(1\sim k - 1\) 都成立。

那么 \(f(k) = 1 + 1 + 2 + 4 + \cdots + 2^{k - 1} = 2^k\)。

因此成立。

又因为总的点数是 \(n\) 个。

所以 \(k = \log_2{n}\)。

因此一个点的 \(mex\) 是在 \(\mathcal{O}(\log n)\) 级别的。

所以我们只需要在 \(\mathcal{O}(n\log n)\) 的时间内，就可以算出答案了。

具体地，我们令 \(dp[x][i]\) 表示遍历到了 \(x\)，当前的 \(mex\) 为 \(i\) 的总方案数。

再令 \(f[0/1][i]\)，表示当前的子节点的 \(mex\) 中，有哪些数出现了的方案数（0/1 是滚动数组， \(i\) 是二进制下的一个数）。

我们可以先预处理出对于每个二进制 \(i\)，它的 \(mex\) 是多少。

然后我们考虑显然我们要维护一个当前节点的 \(mex\) 的最大取值。

那我们就利用子节点的 \(mex\) 的最大取值，先令当前节点的 \(mex\) 的最大取值（以下简称 \(maxmex\)）为 \(0\)。

然后对所有子节点的 \(mex\) 的最大取值 \(sort\) 一遍。

然后再从小到大枚举，如果当前枚举到的值 \(\geq\) \(maxmex\)。

我们就让 \(maxmex\) 加一。

至于为什么嘛 \(\dots\)

可以好好想一想。

然后转移看我的代码就行了。

#include <iostream>
#include <vector>
#include <algorithm>

using std::cin;
using std::cout;
const int N = 2e5 + 10;
const int p = 998244353;

int max[(1 << 22)];
int mex[(1 << 22)];
int f[2][(1 << 22)];
int dp[N][22];
std::vector<int> now[N];
std::vector<int> e[N];

void dfs(int x, int fa)
{
	if (x != 1 && (e[x].size() == 0 || e[x].size() == 1))
	{
		dp[x][1] = dp[x][0] = 1;
		max[x] = 1;
		return;
	}
	for (auto to : e[x])
	{
		if (to != fa)
			dfs(to, x);
		if (to != fa)
			now[x].push_back(max[to]);
	}
	int nowmax = 0;
	std::sort(now[x].begin(), now[x].end());
	for (auto it : now[x])
	{
		if (it >= nowmax)
			nowmax++;
	}
	max[x] = nowmax;
	int opt = 0;
	f[0][0] = 1;
	for (auto to : e[x])
	{
		if (to == fa)
			continue;
		for (int i = 0; i < (1 << (nowmax + 1)); ++i)
			f[opt ^ 1][i] = 0;
		for (int i = 0; i < (1 << (nowmax + 1)); ++i)
		{
			for (int j = 0; j <= max[to]; ++j)
			{
				if (j <= nowmax)
					f[opt ^ 1][i | (1 << j)] = (1ll * f[opt ^ 1][i | (1 << j)] + 1ll * f[opt][i] * dp[to][j] % p) % p;
				else
					f[opt ^ 1][i] = (1ll * f[opt ^ 1][i] + 1ll * f[opt][i] * dp[to][j] % p) % p;
			}
		}
		opt ^= 1;
	}
	for (int i = 0; i < (1 << (nowmax + 1)); ++i)
		dp[x][mex[i]] = (1ll * dp[x][mex[i]] + f[opt][i]) % p;
	for (int i = 0; i < (1 << (nowmax + 1)); ++i)
		f[0][i] = f[1][i] = 0;
}

int main()
{
	int n;
	cin >> n;
	for (int i = 2; i <= n; ++i)
	{
		int fa;
		cin >> fa;
		e[i].push_back(fa);
		e[fa].push_back(i);
	}
	for (int i = 0; i < (1 << 21); ++i)
	{
		while (i & (1 << mex[i]))
			mex[i]++;
	}
	dfs(1, 0);
	for (int i = 0; i <= max[1]; ++i)
		cout << dp[1][i] << '\n';
	for (int i = max[1] + 1; i <= n; ++i)
		cout << 0 << '\n';
	return 0;
}

至于T3和T4，等我会了在写吧 \(\dots\)

（还有就是，这道题是个细节题， TLE 或 RE 了，大概率就是超时了，而且只需要优化一点点，不用整体调整；有问题记得在底下评论发哦~）