正睿25csp七连测day5

题面：











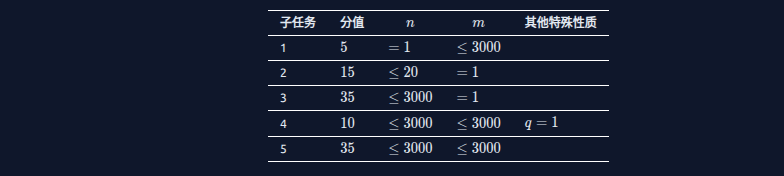
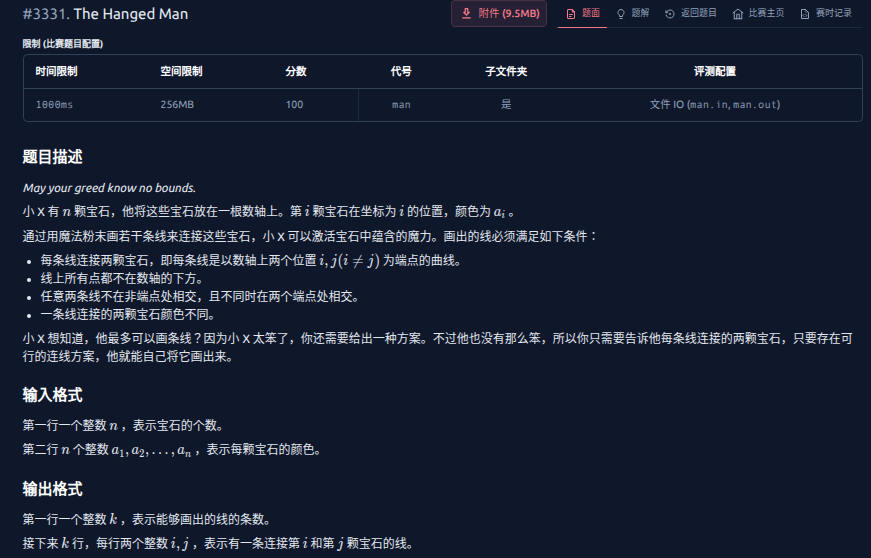
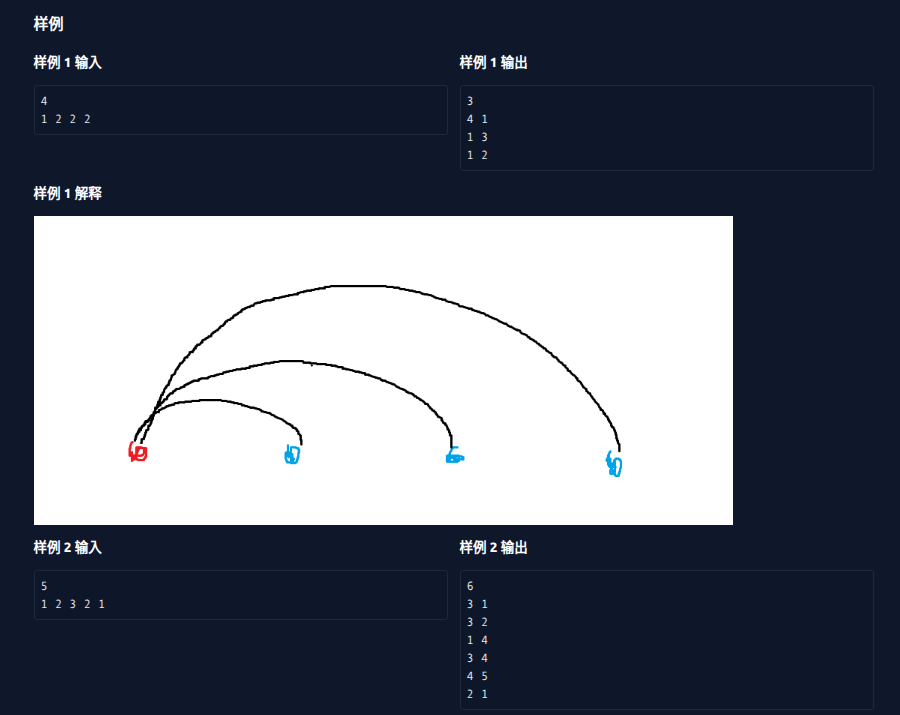
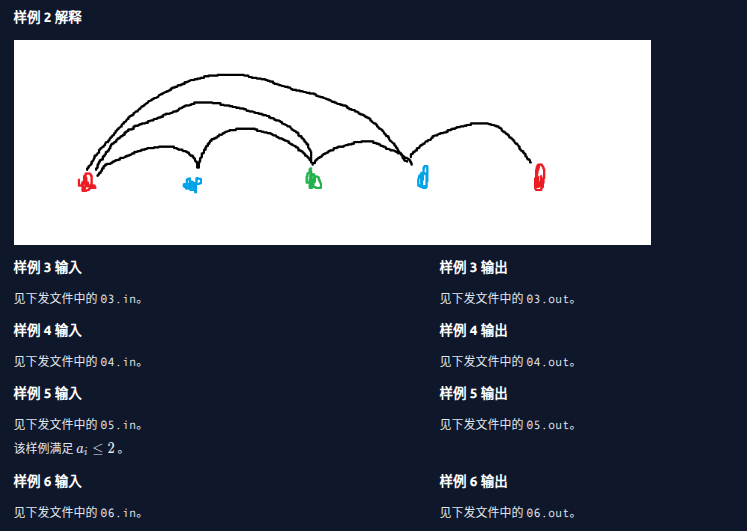
这场打得很飞舞，\(40pts,rk54\)。

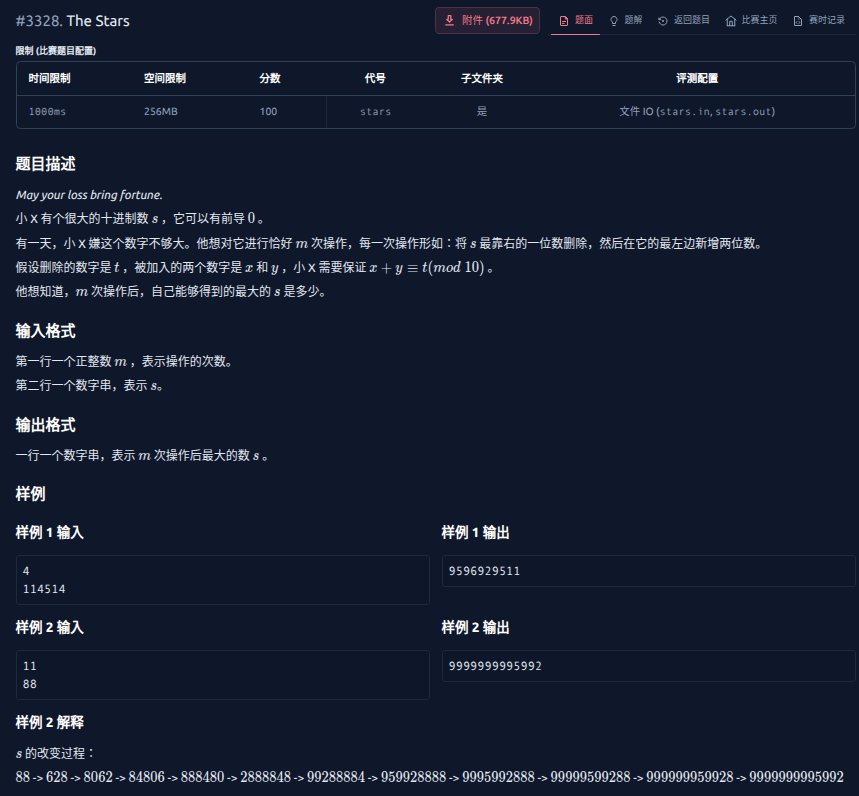
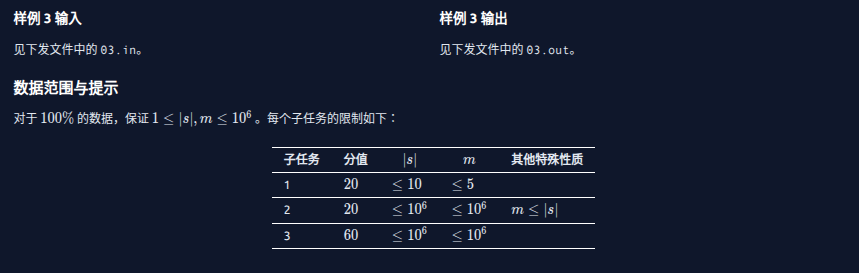
T1

这道题比较考验思维。
我们可以考虑每个点是从最初序列的哪个位置转移过来了（记为 \(from\)）。
不难发现，如果最终序列中的几个位置的 \(from\) 相等，那么这几个位置代表的数的和肯定模 \(10\) 同余于 \(from\) 代表的值。
于是，我们可以利用这个性质（我们不妨叫他性质 \(1\)），贪心地往每个位置里放数，即假设这 \(k\) 个数拥有相等 \(from\)，那么我们可以把最高位的那 \(k - 1\) 个位置填上 \(9\)，剩下的位置根据那几个 \(9\) 和性质 \(1\) 来放最后一个位置。

#include <iostream>
#include <algorithm>
#include <vector>
#define pii std::pair<int, int>

using std::cin;
using std::cout;
const int N = 1e6 + 10;

int n;
int cnt[N];
int num[N];
int fr[3 * N];
int ans[3 * N];
int from[3 * N];
std::vector<pii> v;

int main()
{
	int m;
	cin >> m;
	char c = getchar();
	while (!isdigit(c))
		c = getchar();
	while (isdigit(c))
	{
		num[++n] = c - '0';
		c = getchar();
	}
	std::reverse(num + 1, num + n + 1);
	int l = 1;
	int r = n;
	for (int i = 1; i <= m; ++i)
	{
		fr[++r] = l;
		fr[++r] = l;
		l++;
	}
	int i;
	for (i = 1; i <= n; ++i)
		from[i] = i;
	for (; i <= n + 2 * m; ++i)
		from[i] = from[fr[i]];
	for (int i = l; i <= r; ++i)
	{
		cnt[from[i]]++;
		v.emplace_back(from[i], i);
	}
	std::sort(v.begin(), v.end());
	int now = 0;
	for (auto it : v)
	{
		if (now != it.first)
		{
			now = it.first;
			ans[it.second] = (num[now] - 1ll * (cnt[now] - 1) * 9 % 10 + 10) % 10;
		}
		else
			ans[it.second] = 9;
	}
	for (int i = r; i >= l; --i)
		cout << ans[i];
	cout << '\n';
	return 0;
}

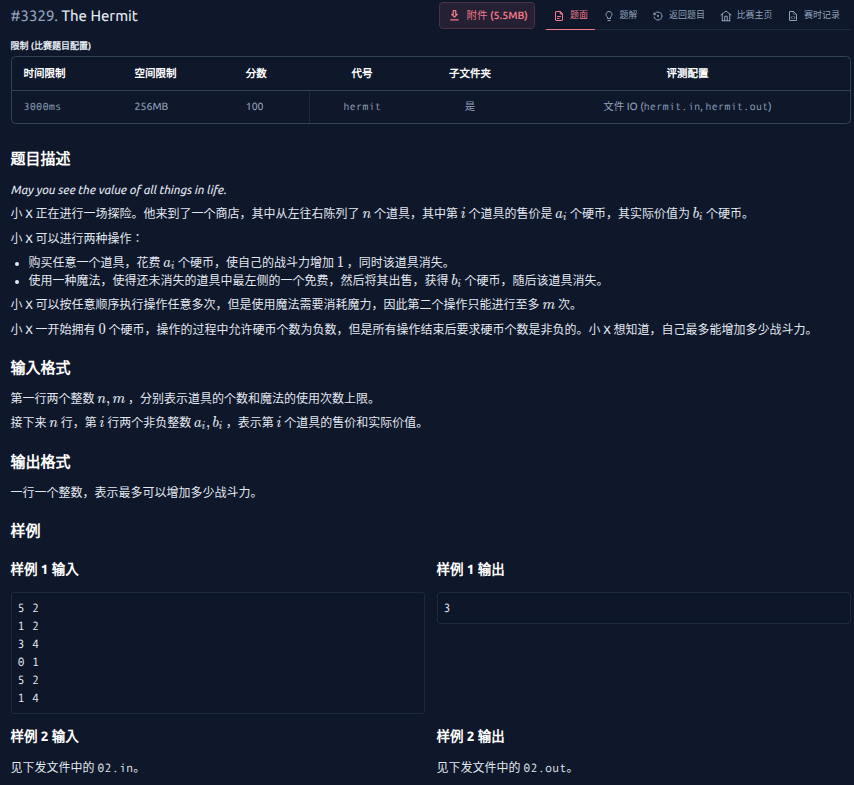
T2

操作的过程中允许硬币个数为负数。

为了使这个问题更加容易解决，我们可以枚举最后一个被购买的物品 \(p\)（因而这个物品必须存在，即只有这个物品前面的物品才能被卖掉）。

然后我们认为，我们现在一共有 \(\sum_{i=1}^p b_i\) 个硬币，并考虑左边的道具如果购买，将会花掉 \(a_i + b_i\) 个硬币，因为我们多算了它的 \(b_i\)，右面的道具还是 \(a_i\) 个硬币。

同时，因为我们最多只能卖掉 \(m\) 个物品，因此我们必须从前面的物品中至少买 \(p - m\) 个，这样剩下的物品就会不多于 \(m\) 个了。

如果我们最后出售了 \(<\) \(m\) 个道具，那么我们一定购买了剩余的所有的道具。

这个很容易证明。

这种情况的话我们可以直接贪心看我们最多能选多少个物品。

因此只考虑恰好购买 \(m\) 个道具的情况。

我们维护一个小根堆和一棵权值线段树。

我们每一次都将 \(a_i + b_i\) 放进堆里面。

如果我们可以开始购买了，我们就开始选堆里最小的。

前面的必须选 \(p - m\) 个，而后面的我们可以使用线段树二分，求得最多可以购买的数量。

当 \(p\) 增加 \(1\) 的时候，我们只需要在线段树上减去一个值，并在堆里 push 一个值就行。

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>

using std::cin;
using std::cout;
typedef long long ll;
const int N = 5e5 + 10;
struct Node
{
	ll sum;
	ll cnt;
	friend Node operator+(const Node &l, const Node &r)
	{
		Node ret;
		ret.sum = l.sum + r.sum;
		ret.cnt = l.cnt + r.cnt;
		return ret;
	}	
} z[N << 2];

#define root 1, cn, 1
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1

int a[N];
int b[N];
int cnt[N];
int map[N];
int truth[N];
std::vector<int> v;
std::vector<int> test;
std::priority_queue<int, std::vector<int>, std::greater<int> > q;

void build(int l, int r, int rt)
{
	if (l == r)
	{
		z[rt].cnt = cnt[l];
		z[rt].sum = 1ll * cnt[l] * truth[l];
		return;
	}
	int mid = (l + r) >> 1;
	build(lson);
	build(rson);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
void minus(int l, int r, int rt, int p)
{
	if (l == r)
	{
		z[rt].cnt--;
		z[rt].sum -= truth[l];
		return;
	}
	int mid = (l + r) >> 1;
	if (p <= mid)
		minus(lson, p);
	else
		minus(rson, p);
	z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
int query(int l, int r, int rt, ll s)
{
	if (z[rt].sum <= s)
		return z[rt].cnt;
	if (l == r)
		return std::min(z[rt].cnt, s / truth[l]);
	int mid = (l + r) >> 1;
	if (z[rt << 1].sum > s)
		return query(lson, s);
	return z[rt << 1].cnt + query(rson, s - z[rt << 1].sum);
}

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)
		cin >> a[i] >> b[i];
	for (int i = 1; i <= n; ++i)
		v.push_back(a[i]);
	std::sort(v.begin(), v.end());
	v.erase(std::unique(v.begin(), v.end()), v.end());
	int cn = 0;
	for (int i = 1; i <= n; ++i)
	{
		map[i] = std::lower_bound(v.begin(), v.end(), a[i]) - v.begin() + 1;
		truth[map[i]] = a[i];
		cn += !cnt[map[i]];
		cnt[map[i]]++;
	}
	build(root);
	ll sum = 0;
	int ans = 0;
	for (int i = 1; i <= n; ++i)
	{
		sum += b[i];
		q.push(a[i] + b[i]);
		minus(root, map[i]);
		if (i < m)
			continue;
		if (i != m)
		{
			sum -= q.top();
			q.pop();
		}
		if (sum < 0)
			continue;
		ans = std::max(ans, i - m + query(root, sum));
	}
	ll tot = 0;
	for (int i = 1; i <= n; ++i)
	{
		tot += b[i];
		test.push_back(a[i] + b[i]);
	}
	std::sort(test.begin(), test.end());
	for (int i = 0; i < n; ++i)
	{
		if (test[i] > tot)
		{
			if (i < n - sum)
			{
				cout << ans << '\n';
				return 0;
			}
			cout << i << '\n';
			return 0;
		}
		tot -= test[i];
	}
	cout << n << '\n';
	return 0;
}

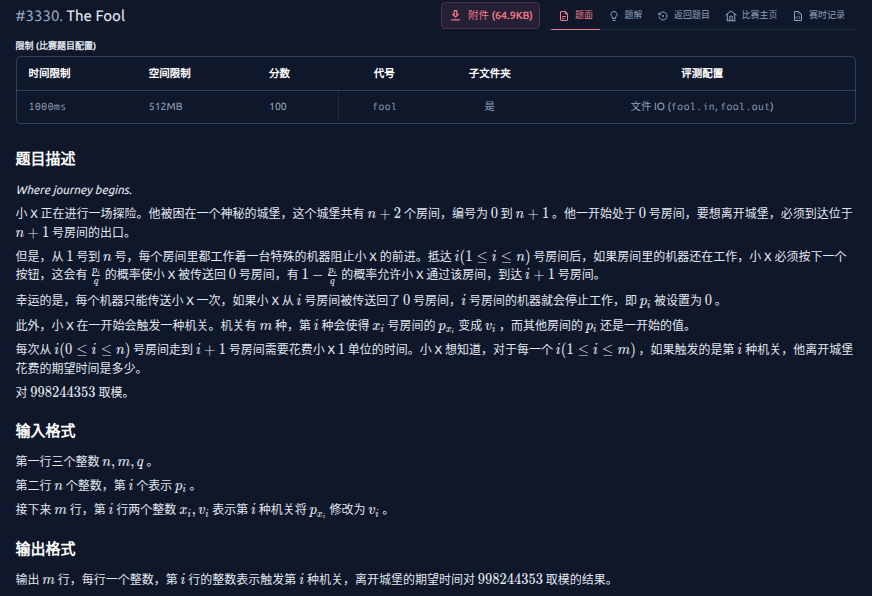
T3、T4等我会了再写吧。