[安乐椅#15] 杨辉三角质数分布性质

性质内容

杨辉三角中，质数仅存在于第2层.

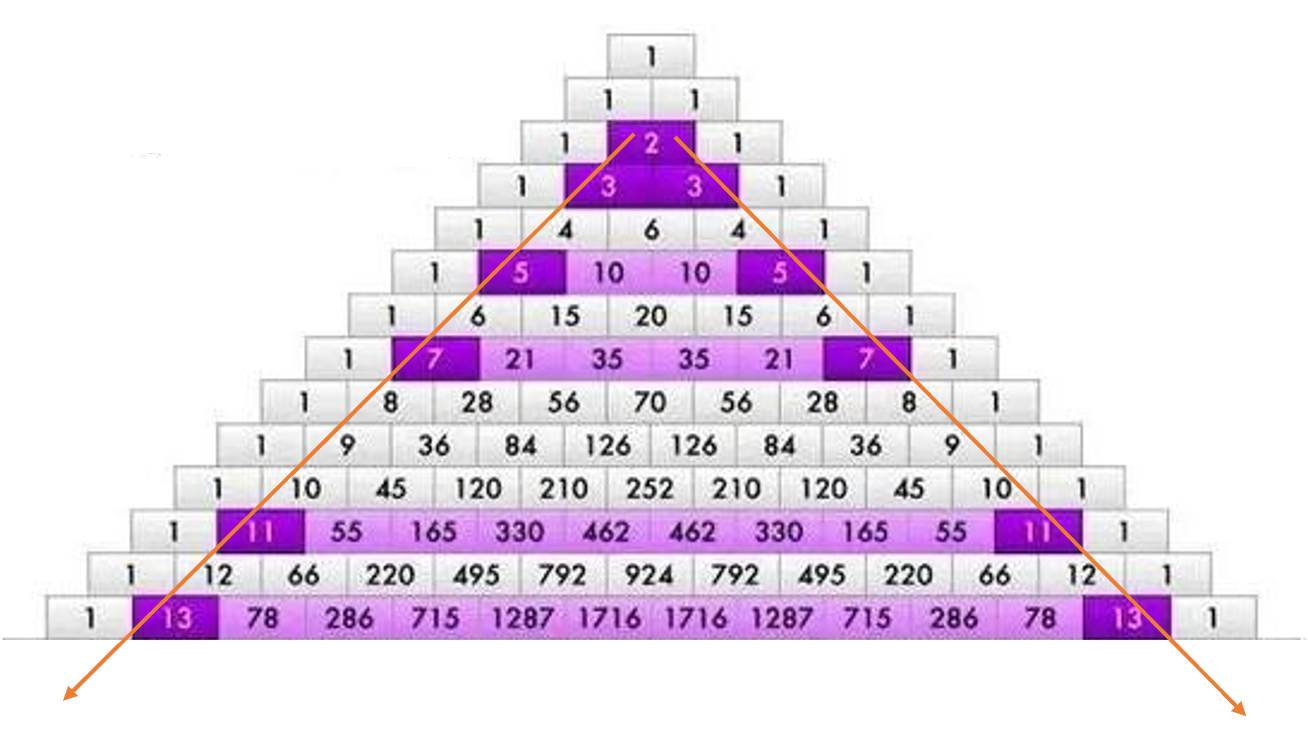
性质证明

一步转化：杨辉三角第 \(n\) 行 \(m\) 列的数为 \(C_n^m\)。原命题转化为 \(C_n^m\) 仅当 \(m=1\) 或 \(n-1\) 时为质数。

对于 \(C_n^m,m \in [2,n-2],m\in \mathbf{N}\)

由单调性知 \(C_n^m>c_n^1=n\) ①

而 \(C_n^m=\dfrac{n!}{m!(n-m)!}\)

故 \(C_n^m\) 所有质因子均小于等于 \(n\) ②

假设 \(C_n^m\) 为质数，则其含有质因子 \(C_n^m\)

由 ① 知 \(C_n^m>n\)

由 ② 知 \(C_n^m\le n\)

矛盾，故 \(C_n^m\) 为合数。

\(\Box\)