
2021年7月2日
摘要:
已知$E$,$F$分别是长方体$ABCD - $的棱$AB$,$A_1B_1$的中点,若$AB=2\sqrt{2}$,\(AD=A{A_1}=2\),则四面体$-DEF$的外接球的表面积为$\underline{\qquad\qquad}$.
阅读全文
posted @ 2021-07-02 09:35
狮山数学
阅读(79)
推荐(0)

2021年6月21日
摘要:
欧拉-查柏(Euler-Chapple)公式的内容为: \(|O_1O_2|^2=R^2-2R\cdot r\) (其中$O_1$、$O_2$为$\triangle ABC$外心、内心,\(R\)、$r$为圆$O_1$、圆$O_2$半径),而且此命题的逆命题也是正确的。 此公式的一种理解方式是,如图
阅读全文
posted @ 2021-06-21 19:51
狮山数学
阅读(775)
推荐(0)

2021年6月18日
摘要:
已知椭圆$C$:$\frac{x2}{a2}+\frac{y2}{b2}=1(a>b>0)$的左顶点和上顶点分别为$A$,\(B\),左、右焦点分别是$F_1$,\(F_2\),在线段$AB$上有且只有一个点$P$满足$PF_1\bot PF_2$,则椭圆的离心率的平方为( \ ) \(A.\fra
阅读全文
posted @ 2021-06-18 17:53
狮山数学
阅读(89)
推荐(0)

2021年6月8日
摘要:
已知$a>0$且$a\neq 1$,函数$f(x)=\frac{xa}{ax}(x>0)$. $(1)$当$a=2$时,求$f(x)$的单调区间; $(2)$若曲线$y=f(x)$与直线$y=1$有且只有两个交点,求$a$的取值范围. 分析:两种方法都需要同学们自己下来完善哈 法一:对函数$f(x)
阅读全文
posted @ 2021-06-08 21:31
狮山数学
阅读(324)
推荐(0)

2021年5月26日
摘要:
已知函数$\textit{f}(\textit{x})=\textit{a}\ln\textit{x}+\textit{x}$, $\textit{x}\in(0$,$+\infty)\text{且}\textit{a}\in\textbf{R}$. $(1)$讨论函数$\textit{f}(\te
阅读全文
posted @ 2021-05-26 19:58
狮山数学
阅读(266)
推荐(0)

2021年1月30日
摘要:
已知抛物线$y^2=2x$的焦点为$F$,该抛物线上有三点$A$,\(B\),\(C\),其中$A,B,F$三点共线,直线$AB$与$AC$ 的倾斜角互补,且$AB\bot BC$,则点$A$的横坐标为$\underline{\qquad\qquad}.$ 容易观察出,两个三角形都是等腰三角形,也就
阅读全文
posted @ 2021-01-30 13:33
狮山数学
阅读(1273)
推荐(0)

2021年1月27日
摘要:
点$E$为$x$轴正半轴上的一点,过点$E$的直线交抛物线$C$:$y^2=4x$于$A$、$B$两点,$F$为$C$的焦点, 直线$AF$、$BF$分别与抛物线$C$交于异于$A$、$B$的$P$、$Q$两点.当直线$AB$,$PQ$的斜率都存在时,分别记为$k_{_1}$、$k_{_2}$. 若
阅读全文
posted @ 2021-01-27 21:39
狮山数学
阅读(687)
推荐(0)

2020年12月22日
摘要:
###相关系数$r=\cos<\overrightarrow\(,\)\overrightarrow>=\frac{\sum\limits_^n(x_-\bar)(y_-\bar)}{\sqrt{\sum\limits_^n(x_-\bar)^2 \sum\limits_^n(y_-\bar)^2}
阅读全文
posted @ 2020-12-22 08:39
狮山数学
阅读(1492)
推荐(0)

2020年7月12日
摘要:
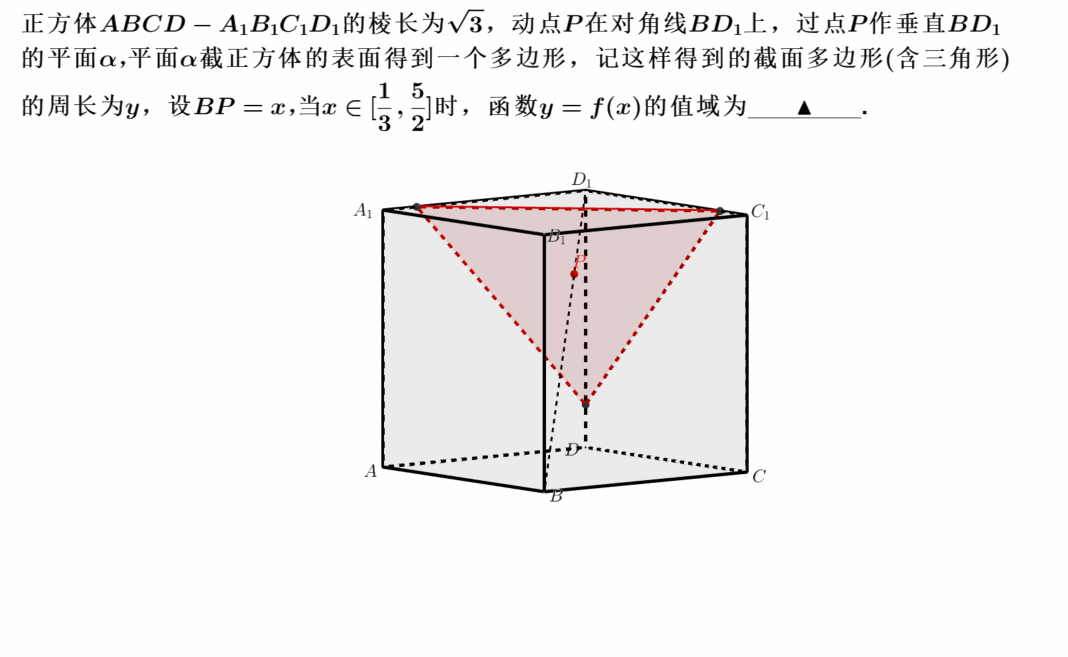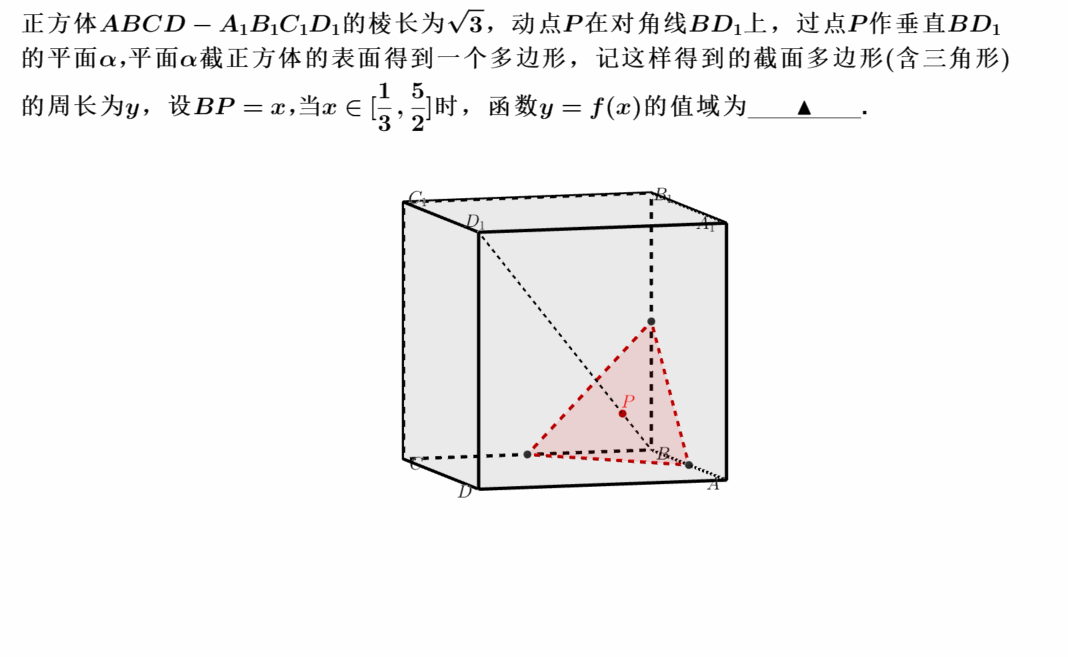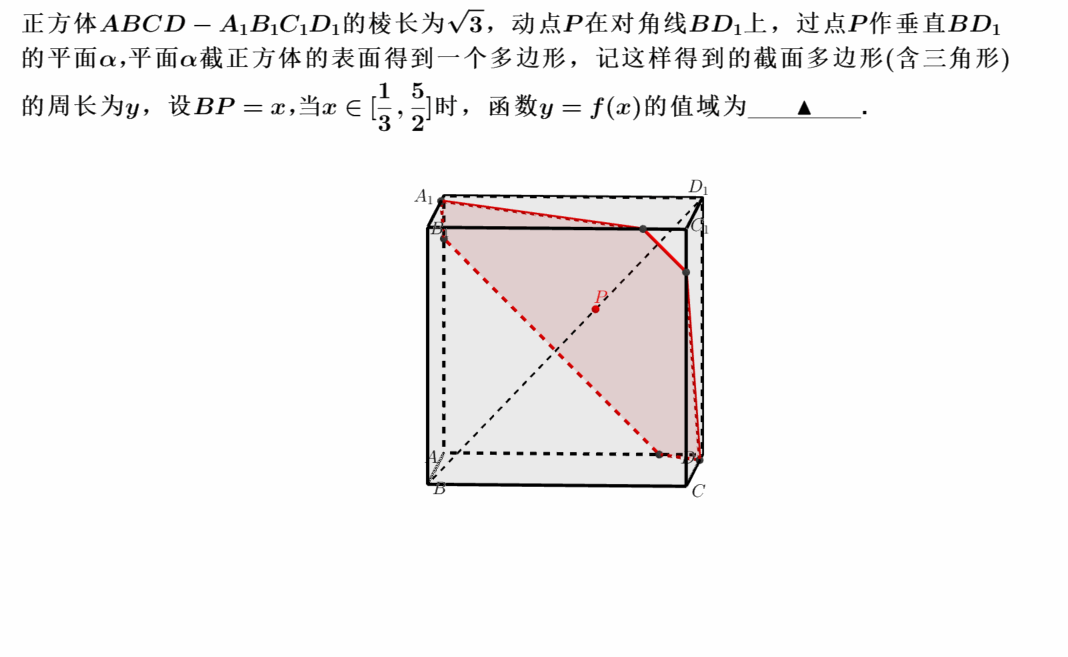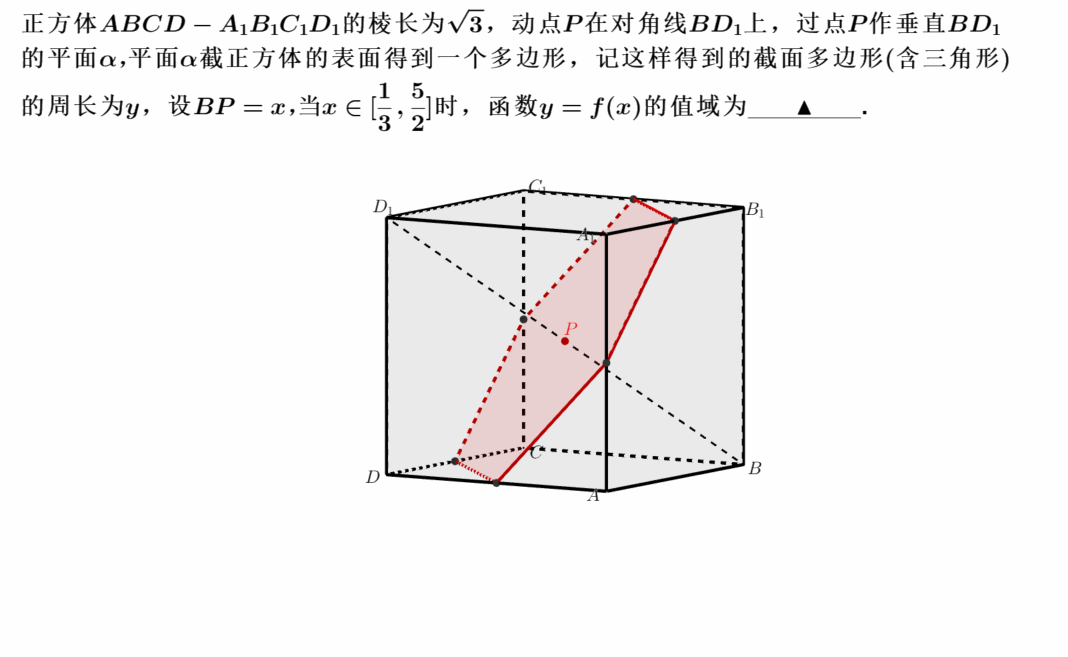
阅读全文
posted @ 2020-07-12 22:28
狮山数学
阅读(186)
推荐(0)

2020年7月7日
摘要:
已知$a,b,c\in\mathrm{R},a+b+c=0,abc=1.\;\;(1)$证明:$ab+bc+ca (1)法一:$2(ab+bc+ca)=(a+b+c)2-(a2+b2+c2)=0-(a2+b2+c^2)<0 $(贵老师的) 法二: 情况\ding{192}当$c<0$时,此时$a+b
阅读全文
posted @ 2020-07-07 20:11
狮山数学
阅读(635)
推荐(0)