常见概率分布与采样方法

均匀分布与高斯分布

如何由均匀分布生成标准正态分布？并且用python实现。^normal

给你一个0到1的均匀分布，如何近似地生成一个均值为0，标准差为1的标准正态分布。你只能用 numpy.random.uniform() 这个函数，然后通过自己的一些算法，实现 numpy.random.normal() 。

解法1:

考察的是中心极限定理和均匀分布。一组大量随机变量的均值符合正态分布。

服从 U(a, b) 均匀分布的随机变量的方差是\((a - b)^2 / 12\)。含有 n 个样本的样本均值\(\bar X\)的方差是\((a - b)^2 / 12 / n\)。

np.random.uniform() 生成的是(0, 1)之间均匀分布的随机数， 2 * np.random.uniform() - 1生成的是(-1, 1)之间均匀分布的随机数。此时均值的方差为1/(3n).

import numpy as np
import math
n = 300 # 样本数量,以300为例,为使标准差为1,须乘以30
normal_rv = math.sqrt(3 * n) * np.mean(2 * np.random.uniform(size=n) - 1)

上面得到的 normal_rv 就是一个标准正态分布随机变量。

解法2:

问题要求的是近似的正态，其实完全可以精确的正态。Box-Muller 变换就能做到这一点。

假设 i.i.d. X1,X2∼U(0,1)，也就是服从(0, 1)均匀分布，那么通过下面这个Box-Muller变换:

\[Z=\sqrt{−2\ln(X_1)}\cos⁡(2πX_2) \]

得到的变量 Z 就是服从 N(0,1) 标准正态分布的随机变量。

均匀分布的变量X,Y,Z,...相加后是什么分布?

n个均匀分布随机变量相加得到的新的随机变量符合高斯分布，这叫中心极限定理。应该叫大致符合高斯分布，当n趋于无穷时符合高斯分布。且不论原始分布为何分布。高斯分布，也称正态分布，又称常态分布。

能否由高斯分布得到均匀分布?

标准正态分布，那么能否将它转换成(0,1)区间上的均匀分布?

解析：
生成两个独立的正太分布变量Z0,Z1,然后arctan(z0/z1)/(2pi)+0.5，可以生成0-1均匀分布的变量.
可以通过程序验证。

高斯分布的和仍然是高斯分布

如果 \(X\sim N(\mu_{X} ,\sigma_{X}^{2}), Y\sim N(\mu_{Y} ,\sigma_{Y}^{2})\) 是统计独立的常态随机变量，那么它们的和也满足正态分布\(U=X+Y\sim N(\mu_{X}+\mu_{Y} ,\sigma_{X}^{2}+\sigma_{Y}^{2})\). 证明过程见维基百科 Sum of normally distributed random variables

样本均值服从什么分布

随机变量X是任意的分布, 求均值\(\bar X\)服从的分布.
由中心极限定理, 当抽样个数n比较大时, \(\bar X\)服从近似正态分布 \(\bar X\sim N(\mu,{\sigma^2\over n})\):

\[E(\bar X)=E({1\over n}\sum_{i=1}^n X_i)={1\over n}\sum_{i=1}^n E(X_i)=\mu \\ D(\bar X)=D({1\over n}\sum_{i=1}^n X_i)={1\over n^2}\sum_{i=1}^n D(X_i)={\sigma^2\over n} \]

单位圆、球面均匀分布

如何生成分布在单位圆、单位球体表面上的点的随机样本？

也就是生成(x, y, z)的联合概率分布服从均匀分布，不能通过均匀分布随机生成(x,y)然后通过\(\sqrt{1-x^2-y^2}\) 的方式得到z。

解：随机生成三个服从标准正态分布的变量,归一化后的(x,y,z)是单位球面上的均匀随机点.

给定n个独立同分布的标准正态分布的变量X=(X1,X2,…,Xn) iid ∼N(0,1), 那么有\(X/\sqrt{X_1^2+\cdots+X_n^2}\)服从单位球面上的均匀分布.

证明^uni:

标准正态分布的概率密度函数为:

\[f(x) = \frac{1}{\sqrt{2\pi}}e^{- \frac{1}{2}x^2} \]

那么三个变量的联合概率密度函数为(独立同分布,所以直接相乘):

\[f(x,y,z)=f(v)= \left(\frac{1}{\sqrt{2\pi}}e^{- \frac{1}{2}x^2} \right) \left(\frac{1}{\sqrt{2\pi}}e^{- \frac{1}{2}y^2} \right) \left(\frac{1}{\sqrt{2\pi}}e^{- \frac{1}{2}z^2} \right) \\ = \frac{1}{(2\pi)^\frac{3}{2}}e^{- \frac{1}{2}(x^2+y^2+z^2)} = \frac{1}{(2\pi)^\frac{3}{2}}e^{- \frac{1}{2}\|v\|^2}. \]

当\(v^2=x^2+y^2+z^2=1\) 时 \(f(x,y,z)\) 是个常数,因此是均匀分布.

扩展问题：

那么如何生成单位圆内或单位球体内的均匀分布的点呢?
需要看如何定义均匀的概念了, 不同的定义方式结果可能不同, 参考贝特朗悖论.

如果定义为面积上的均匀分布，在单位圆内随机选点，可以生成均匀分布的半径与角度 \((r,\theta)\) ,由正余弦求出x,y坐标。

• https://www.zhihu.com/question/26579222
• http://mathworld.wolfram.com/SpherePointPicking.html

伯努利分布与高斯分布

伯努利分布与高斯分布什么关系？

著名的Central Limit Theorem（中心极限定理）说的是，任何变量（不管什么分布）的平均数在样本量达到足够大的时候都会变成正态分布。

二项分布（Binomial Distribution）是一种离散型概率分布，又称为「n 重伯努利分布」。Binomial分布的极限是Gaussian分布。

• bernoulli分布就像是一次实验的结果. 就是一次投硬币的结果.
• 二项分布是n次berboulli实验结果的求和，就是很多次投硬币的一个分布.
• 而高斯分布是无穷次实验的结果。高斯分布可以被二项分布去逼近，是一种极限场景.

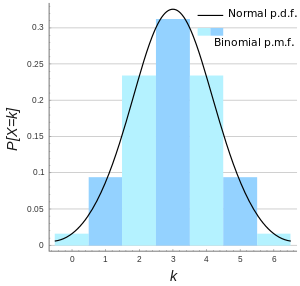
参考：关于Bernoulli，Binomial，Gaussian分布的关系？

采样方法

随机模拟也可以叫做蒙特卡罗模拟(Monte Carlo Simulation)，研究的问题是给定一个概率分布 p(x) ，如何在计算机中生成它的样本，即抽样（sampling）。
对于机器学习模型而言，优化整体分布上的期望风险不切实际，需要通过采样得到近似分布，对经验风险进行优化。对于一些比较复杂的模型或者含有隐变量的模型，还可利用采样方法进行随机模拟得到复杂模型的近似解。

在各类概率抽样方法中均需要用到均匀分布随机数，比如以概率p决定是否采样某个样本，可以通过生成0~1之间均匀分布的随机变量与p比较大小。对于从多个离散变量从抽取单个样本时常用的轮盘赌算法也是直接利用了均匀分布随机数。因此下面首先对均匀分布随机数进行介绍，然后介绍几种采样方法。

参考：

• 《百面机器学习》第8章 采样

均匀分布随机数生成器

由于计算机程序是确定性的，并且只能处理离散状态值（不能无限微分），因此并不能产生真正意义上的完全均匀分布随机数，只能产生伪随机数，并通过离散分布来逼近连续分布。

常用的离散均匀分布伪随机数实现方式为：线性同余法(Linear Congruential Generator)

\[x_{t+1} \equiv a \cdot x_{t}+c\ (\bmod m) \]

通过前一个随机数线性变化并取模迭代生成下一个随机数，得到区间[0,m−1]上的随机整数，除以m得到[0,1]区间的浮点数。

容易看出线性同余法生成的随机序列取决于随机数种子 \(x_0\)，并且具有循环周期。为了提高随机性，应该让循环周期尽可能接近m，这需要选择合适的乘法因子a 和模数m(需要利用代数和群理论)。具体实现中有多种不同的版本，例如gcc中采用的glibc版本: \(a=1103515245,\ c=12345,\ m=2^{31}-1\).

在应用时常常选择当前的时间戳作为随机数种子来生成随机数，但是在共享机器学习模型时往往设置一个固定的随机数种子，方便复现相同的结果。

均匀分布是最易实现的一种随机数分布，通过逆变换可作为其它分布实现的基础。

逆变换采样

如果希望从目标分布P(x)中采样，但是P(x)函数比较复杂不好采样时可以通过函数变换法 ，构造一个变换 \(u=\phi(x)\)，使得从变换后的分布p(u)中采样u比较容易，这样可以通过先对u进行采样然后通过反函数 \(x=\phi^{-1}(u)\) 来间接得到x。

在函数变换法中，如果变换关系φ(·)是x的累积分布函数的话，则称为 逆变换采样(Inverse Transform Sampling)。示意图如下：

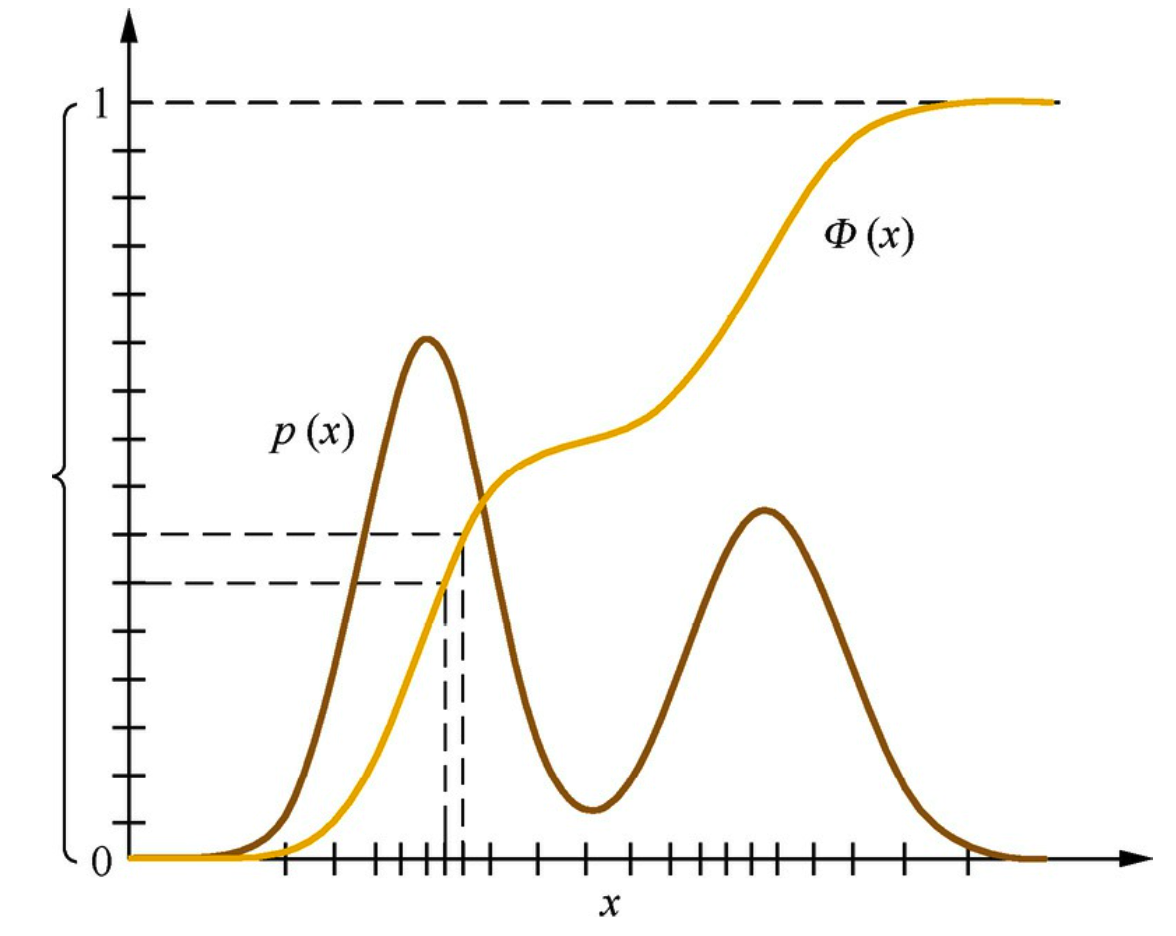
由于严格单调递增的累积分布函数服从均匀分布（严格单调递增是在所有取值概率都大于0的情况下，累积分布函数总是递增的），因此可通过均匀分布采样随机变量u，再通过累积分布函数的反函数得到服从目标分布的随机变量x。因此逆变换采样法理论上适用于任何累积分布可求逆的原分布的随机采样。
不严谨证明严格单调递增的累积分布函数服从均匀分布：参考 怎么证明连续随机变量的累积分布函数的密度函数是均匀分布的？
令 \(Y=F(X)\)，则有\(0 \le Y \le1\). 由于单调递增 ，有

\[P(Y \le y)=P(F(X) \le y)=P(X \le F^{-1}(y))=F(F^{-1}(y))=y \]

所以 \(Y \sim U(0,1)\).
然而如果函数求逆不好求解时无法使用，可以改用参考分布等做法，比如拒绝采样、重要性采样。

拒绝采样&重要性采样

一种常见的用法如已有一个随机生成1~7之间的随机数生成器rand7(), 采用拒绝采样来得到rand5(), 只需要每次采样到6、7时拒绝使用，继续采样即可。

拒绝采样，又叫接受/拒绝采样(Accept-Reject Sampling)。对于目标分布P(x)，选取一个容易采样的参考分布Q(x)，使得对于任意x都有\(P(x)\le MQ(x)\)， 则可以按如下过程进行采样：

1. 从Q(x)中随机抽取一个样本\(x_i\)。
2. 从均匀分布U(0,1)产生一个随机数\(u_i\)。
3. 如果 \(u_i\le {P(x_i)\over MQ(x_i)}\)，则接受该样本；否则拒绝，重新从步骤1开始执行，直到新产生的样本被接受。

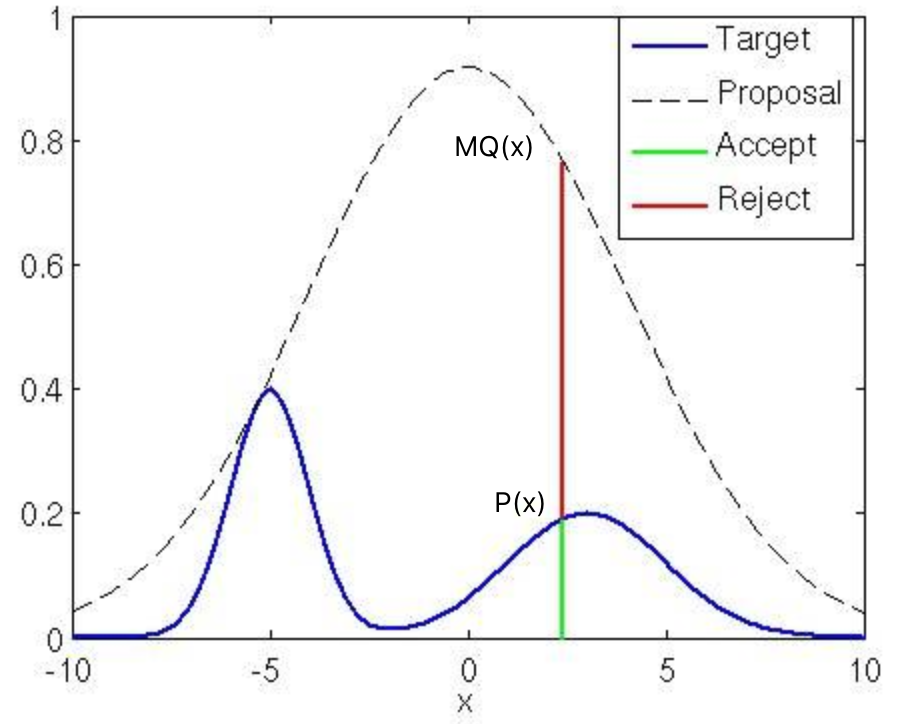
其中包络函数M·Q(x)的曲线紧紧包裹P(x)曲线，包裹越紧越逼近，采样时被接受的概率越大，采样效率越高。

对Q(x)乘M的原因是P(x)、Q(x)的积分都是1，不可能完全包裹，必须乘一个大于1的系数M，并且这个M尽量接近于1以提高效率。

重要性采样，将\(W(x_i)={P(x_i)\over Q(x_i)}\) 视为样本的重要性权重。 从参考分布Q(x)中抽取N个样本，然后按照它们对应的重要性权重对这些样本进行重新采样。可以看出这种方式和拒绝采样思路非常相似，均利用了较易采样的分布Q(x)，但相比拒绝采样法，每次采样不会拒绝。

缺点：

拒绝采样和重要性重采样不适合高维空间的采样，经常难以寻找合适的参考分布。对于高维空间可以考虑马尔可夫蒙特卡洛采样法。

Ziggurat算法

拒绝采样法的效率取决于参考分布与目标分布的接近程度，Ziggurat算法采用多个阶梯矩形来逼近目标分布，采样效率比较高。

高斯分布采样

高斯分布的采样方法比较多，基本都是利用上边的均匀分布采样+逆变换采样/拒绝采样/重要性采样。

由于高斯分布可以由标准正态分布通过拉伸和平移得到，因此这里只考虑标准正态分布的采样。

直接的逆变换法，没有显式解。

(1)产生[0,1]上的均匀分布随机数u。

(2)令 \(z=\sqrt 2 \rm{erf}^{-1} (2u-1)\)，则z服从标准正态分布。其中erf(·)是高斯误差函数：

\[\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} \mathrm{e}^{-t^{2}} \mathrm{~d} t \]

然而 erf(x)的逆函数不是一个初等函数，没有显式解。因此这种直接的逆变换法不容易求解，也不会使用。

Box-Muller 采样法：联合分布与极坐标变换。

用两个独立的高斯分布的联合分布来避免单个随机变量的逆分布变换中不好求逆的问题。因为高维正态分布有特殊的性质：它的每一维的分量都是正态分布；单个维度对于其他维度的条件概率分布也是正态分布。因此Box-Muller方法得到二维的正态分布之后，其每一维度都是正态分布。

假设x,y是两个服从标准正态分布的独立随机变量，它们的联合概率密度为：

\[\begin{align} p(x, y) =p(x)\cdot p(y) &=\frac{1}{2 \pi} \mathrm{e}^{-\frac{x^{2}+y^{2}}{2}} \end{align} \]

考虑对这个联合分布的累积分布进行采样，再通过逆函数变换得到服从正态分布的随机变量。

先看个求解联合分布的定积分的例子：

令 \(I=\int_{-\infty}^{\infty} e^{\frac{-x^{2}}{2}} d x\), 则

\[\mathrm{I}^{2}=\int_{-\infty}^{\infty} \mathrm{e}^{\frac{-x^{2}}{2}} d x \int_{-\infty}^{\infty} \mathrm{e}^{\frac{-y^{2}}{2}} d y=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathrm{e}^{-\frac{x^{2}+y^{2}}{2}} d x d y \]

通过极坐标变换（x,y）-> (r, θ)，令 \(\mathrm{x}=\mathrm{r} \cos \theta, \mathrm{y}=\mathrm{r} \sin \theta\), 则有 \(r^2=x^2+y^2\)，\(r^2\) 是点(x,y)到原点的距离的平方。

\[\mathrm{I}^{2}=\int_{0}^{2 \pi} \int_{0}^{\infty} \mathrm{e}^{-\frac{\mathrm{r}^{2}}{2}} \mathrm{rdr} \mathrm{d} \theta =2 \pi \int_{0}^{\infty} \mathrm{e}^{-\frac{\mathrm{r}^{2}}{2}} \mathrm{rdr} =\left . -2 \pi e^{-{r^2\over 2}} \right |_0^\infty =2 \pi \]

稍改下就能得到(x,y)的联合概率分布的累积分布的式子：

\[\begin{align} P(X\le x,Y\le y) &= \int_{-\infty}^x \int_{-\infty}^y \frac{1}{2 \pi} \mathrm{e}^{-\frac{u^{2}+v^{2}} {2}} dudv \\ (x^2+y^2= r^2) &\Rightarrow \int_{0}^{2 \pi} \int_{0}^{r} {1\over 2\pi}e^{-\frac{\mathrm{\rho}^{2}}{2}} \mathrm{\rho d\rho} \mathrm{d} \theta = \int_{0}^{r} \mathrm{e}^{-\frac{\mathrm{\rho}^{2}}{2}} \mathrm{\rho d\rho} =\left . - e^{-{\rho^2\over 2}} \right |_0^r \\ &\Rightarrow F(r) =1-\mathrm{e}^{-\frac{r^{2}}{2}}, r \geqslant 0 \end{align} \]

可以得出一个单变量的概率密度累积分布函数 F(r). 其物理意义为点落于圆盘 \(\left\{(x,y)|x^2+y^2\le r^2\right\}\)内的概率。

根据逆变换采样的原理，通过[0,1]区间匀分布产生一个随机变量z，然而通过反函数F'(z)得到随机变量r，再通过极坐标变换到(x,y)就得到了服从正态分布的两个随机变量。这里的角度θ在[0, 2π]内均匀随机采样即可。

其中，反函数 \(F'(z)=\sqrt{-2 \ln(1-z)}\).

由于\(z\sim [0,1]\)，也可使用\(F'(1-z)=\sqrt{-2 \ln(z)}\).

1. 生成服从 [0, 1] 均匀分布的随机变量 u1，利用逆变换采样方法转换成二维平面点半径 \(r=\sqrt{-2 \ln(u1)}\)
2. 生成服从 [0, 1] 均匀分布的随机变量 u2，乘以 2π，即为样本点的角度 θ=2π u2
3. 将 r 和 θ 转换成 x, y 坐标下的点。

\[\begin{cases} x = r \cos(\theta) =\sqrt{-2 \ln u_1} \cos(2 \pi u_2) \\ y = r \sin(\theta) = \sqrt{-2 \ln u_1} \sin(2 \pi u_2) \end{cases} \]

拒绝采样-极坐标方法

Box-Muller 方法还有一种形式，称为极坐标形式（Polar form），属于拒绝采样方法。

Box–Muller 计算公式中包含三角函数，相对比较耗时，而 Marsaglia polar method则避开了三角函数的计算，因而更快。

生成服从 [-1, 1] 均匀分布的随机变量u、v，对落在单位圆外、圆周或圆心的点(u,v)拒绝采样，从而得到单位圆盘内的均匀分布的随机数pair(u,v)。

令 \(s=u^2+v^2\)，由于\(u,v \sim U(-1,1)\)且 s < 1，所以 s 服从 (0, 1) 开区间范围上的均匀分布。并且随机点(u,v)的角度也是均匀分布：\(\theta/2\pi \sim U[0,1]\)。

因此，可以将Box–Muller 计算公式中的cos θ、sin θ替换为 \({u\over \sqrt s}\), \({v\over \sqrt s}\). u1替换成s即可。

参考：

• Box-Muller方法的证明
• Box–Muller transform - Wikipedia

MCMC采样

蒙特卡洛原则与数值积分

Monte Carlo principle：已知随机变量 \(X\sim p(x)\)，计算函数 f(x) 的期望的方法：从\(p(x)\)中抽样\(x_i\)，计算 \(f(x_i)\) 的平均。

对于复杂的函数求积分时不易求解，可以通过数值解法来求近似的结果，常用的方法是蒙特卡洛积分：

\[\int_a^b f(x)dx=\int_a^b {f(x)\over q(x)}q(x)dx \approx {1\over n}\sum_{i}^n {f(x_i)\over q(x_i)} \tag {$x_i \sim q(x),n \to +\infty$} \]

其中q(x)是比较容易采样的任意的分布（比如高斯分布），从q(x)中抽取n个样本，计算 \(f(x_i)/q(x_i)\) 的均值（期望）作为近似积分结果，n越大结果越精确。

重要性抽样也是采用了引入较容易采样的分布的思想。

马尔科夫链与稳态

马尔科夫链（一阶）：是按照一个转移概率矩阵去转移的随机过程。每个状态只与前一个状态有关，而与更早的状态无关。

马氏链的收敛定理：初始状态分布向量 \(π_0\) 在经过若干次转移（转移概率矩阵P）后会达到一个稳定状态，称为平稳分布状态π。π是方程πP=π的唯一非负解，后续的状态转移均满足 πP=π。

关于为什么会达到稳态，参考 方阵的幂序列及收敛性：\(\lim_{n \rightarrow \infty} \boldsymbol{P}^{n}=\boldsymbol{O}\)

有两个必要前提需要满足：

1. irreducible， 所有状态节点需构成一个连通图。
2. aperiodic，非周期性，链条不会在特定的周期内在两个节点来回循环。

马尔科夫链收敛的充分条件是 细致平稳条件（Detailed Balance），对于任意的两个状态 i,j 满足：

\[π_iP_{ij} = π_jP_{ji} \]

证明：

\[\begin{align} && π_iP_{ij} & = π_jP_{ji} \\ \Rightarrow && \sum_i π_iP_{ij} & = \sum_i π_jP_{ji} \\ \Rightarrow && (πP)_j & = π_j\sum_i P_{ji}=π_j \\ \Rightarrow && πP & = π \end{align} \]

其物理含义为：从状态i转移到j的失去的概率质量恰好等于从j转移到i补回来的量，因而在经历一次全量转移之后，每个状态的概率质量保持不变，即平稳状态。

细致平稳条件满足可逆马尔科夫链的性质：一个封闭的环中，一个方向的概率连乘积=反过来方向的概率连乘积。

MCMC

马尔可夫蒙特卡洛(Markov Chain Monte Carlo，MCMC)采样法是沿着马尔科夫链进行采样的蒙特卡洛法，核心是构造一个转移矩阵为P的马尔科夫链，使得该马尔科夫链的平稳分布恰好是待采样的目标分布。不同的马尔可夫链构造方法对应着不同的MCMC采样法，常见的有Metropolis-Hastings采样法和Gibbs采样法（吉布斯采样）。MCMC采样法适用于复杂分布的采样， 并能用于高维空间。最初由 Metropolis 在1953年研究物理学中的粒子系统的平稳性质问题时提出（Metropolis 算法，收录在《统计学中的重大突破》），Metropolis算法被评为二十世纪的十个最重要的算法之一。

所有的 MCMC(Markov Chain Monte Carlo) 方法都是以马氏链的收敛定理作为理论基础，思路为构造出满足条件π(x)=p(x)的转移矩阵之后从随机的初始状态开始进行状态转移，在达到稳态（收敛）之后的马尔科夫链上的样本即满足目标分布的样本。收敛在这里称之为 burning-in，在 burning-in 之前的若干迭代步骤生成的点被抛弃掉。

转移矩阵的构造方法

假设已有一个初始的转移矩阵为Q的马氏链，其稳态分布为q(x)，q(x)是一个比较容易采样的参考分布。

马氏链Q的细致平稳条件为 \(q_iQ_{ij}=q_jQ_{ji}\) ，显然对于我们需要采样的目标分布 \(p(x)\ne q(x)\) 时， \(p_iQ_{ij}\ne p_jQ_{ji}\) . 可以通过修改转移矩阵使p(x)成为某个马氏链的稳态分布，一种方式为对转移矩阵Q乘上接受率矩阵 A（哈达玛积，对应元素相乘），使得 \(p_iQ_{ij}A_{ij} = p_jQ_{ji}A_{ji}\)。此时\(p(x)\)成为新的马氏链（\(Q'=QA\)）的稳态分布，\(A_{ij}\) 的物理含义为接受从状态i向j跳转的概率。那么如何选取矩阵 *A *？按照对称性，可以设置 \(A_{ij} = p_jQ_{ji}\)。然后计算出\(Q'\)进行马氏链随机采样即可。

然而存在的一个问题是，接受率 \(A_{ij}\) 数值偏小（两个<1的小数相乘之后变得更小）导致在生成随机数采样时容易原地踏步，拒绝大量的跳转，这使得状态空间的遍历比较耗时，收敛速度慢。

Metropolis-Hastings 算法 是MCMC改进变种之一，改进方式是从细致平稳条件两边同比例提升数值大小的角度考虑，将数值对 \((A_{ij},A_{ji}) = (p_jQ_{ji},p_iQ_{ij})\)中的较大值放大到1，较小值同比例放大。矩阵 A 巧妙地定义为：

\[A_{ij} = \min\left \{{p_jQ_{ji} \over p_iQ_{ij}}, 1 \right\} \]

Metropolis-Hasting 算法步骤：

1. 初始化，随机选择一个初始状态点 \(x_0\)
2. 循环采样n个点 \(x_i, i\in\{0,1,...n-1\}\)
   • 按参考转移矩阵Q随机采样新状态 x'
   • 均匀分布采样 \(u\sim U[0,1]\)
   • 如果 \(u < A_{ij} = \min\left \{{p_jQ_{ji} \over p_iQ_{ij}}, 1 \right\}\)，接受 x'： \(x_{i+1} =x'\)
   • 否则保持不变： \(x_{i+1} =x_i\)

Metropolis-Hastings 算法 在大数据及高维数据中面临的挑战：

1. 特征维度高
   • 意味着状态空间很大，那么接受率矩阵A的计算复杂度增加。
   • 各特征维度的联合分布不易统计，而容易给出的是条件概率分布。
2. 拒绝转移，和拒绝采样一样面临影响效率的问题。

Gibbs采样法解决了这两个挑战，在大数据时代被广泛应用。

Gibbs采样

在统计学和统计物理学中，Gibbs Sampling 是马尔可夫链蒙特卡尔理论（MCMC）中用来获取一系列近似等于指定多维概率分布（比如2个或者多个随即变量的联合概率分布）观察样本的算法。该算法由Stuart Geman和Donald Geman两兄弟于1984年提出，应用在Gibbs random field的研究之中。这个算法在现代贝叶斯分析中占据重要位置。

Gibbs采样法是Metropolis-Hastings算法的一个特例，其核心思想是利用维度之间的条件概率分布每次只对样本的一个维度进行采样和更新。Gibss采样是需要知道样本中一个属性在其它所有属性下的条件概率，然后利用这个条件概率分布产生各个属性的样本值。

n维Gibbs采样法：

随机初始化 \(\left\{x_{i}: i=1, \cdots, n\right\}\)对 \(t=0,1,2, \cdots\) 循环采样：

1. \(x_{1}^{(t+1)} \sim p\left(x_{1} \mid x_{2}^{(t)}, x_{3}^{(t)}, \cdots, x_{n}^{(t)}\right)\)
2. \(x_{2}^{(t+1)} \sim p\left(x_{2} \mid x_{1}^{(t+1)}, x_{3}^{(t)}, \cdots, x_{n}^{(t)}\right)\)
3. \(\cdots\)
4. \(x_{j}^{(t+1)} \sim p\left(x_{j} \mid x_{1}^{(t+1)}, \cdots, x_{j-1}^{(t+1)}, x_{j+1}^{(t)}, \cdots, x_{n}^{(t)}\right)\)
5. \(\cdots\)
6. \(x_{n}^{(t+1)} \sim p\left(x_{n} \mid x_{1}^{(t+1)}, x_{2}^{t}, \cdots, x_{n-1}^{(t+1)}\right)\)

算法收敛后（burning-in，设定状态转移次数阈值）继续采样得到服从多维联合概率分布p(x1,x2,⋯,xn)的样本。

采样过程与坐标下降法非常相似，但是坐标轴轮换不是必须的，每次可以随机选择某一个坐标轴进行状态转移，一样能够达到收敛状态，但通常会采用坐标轴轮换这种确定性的过程。

原理：Gibbs采样为什么能收敛到稳态？为什么不需要接受率了？

多维概率分布 p 的完全条件概率(full conditionals)定义为：

\[p\left(x_{j} \mid x_{\neg j}\right) ={p(x) \over p(x_{\neg j})} =p\left(x_{j} \mid x_{1}, \ldots, x_{j-1}, x_{j+1}, \ldots, x_{n}\right) =\frac{p\left(x_{1}, \ldots, x_{n}\right)}{p\left(x_{1}, \ldots, x_{j-1}, x_{j+1}, \ldots, x_{n}\right)} \]

将转移概率矩阵Q中 \(a\to b\) 的概率定义为：

\[Q_{a\to b}= \begin{cases} p(x_j^b|x_{\neg j}^a) && x_{\neg j}^a=x_{\neg j}^b \\ 0 && x_{\neg j}^a \ne x_{\neg j}^b \\ \end{cases} \]

即将坐标轴方向上点之间的转移概率设为完全条件概率，非坐标轴之间的点拒绝转移。将这个矩阵作为参考转移矩阵，使得接受率始终为1。证明如下：

\[\begin{align} A_{a\to b} &= \min\left \{{p_bQ_{b\to a} \over p_aQ_{a\to b}}, 1 \right\} \\ &= \min\left \{ {p_b p(x_j^a|x_{\neg j}^b) \over p_a p(x_j^b|x_{\neg j}^a) }, 1 \right\} & \left( p(x)=p(x_j|x_{\neg j}) p(x_{\neg j})\right ) \\ &= \min\left \{ { p(x_j^b|x_{\neg j}^b) p(x_{\neg j}^b) p(x_j^a|x_{\neg j}^b) \over p(x_j^a|x_{\neg j}^a) p(x_{\neg j}^a) p(x_j^b|x_{\neg j}^a) }, 1 \right\} & (x_{\neg j}^a=x_{\neg j}^b) \\ &= \min\left \{ 1, 1 \right\} = 1 \end{align} \]

接受率为1意味着直接满足了细致平稳条件：\(p_a Q_{a\to b} = p_b Q_{b\to a}\). 按照这种沿坐标轴转移的概率矩阵Q，就能够达到稳态。

因此，只要在联合概率的 full conditionals 可用时，可以采用 n 维向量里每一个维度循环的方式来迭代达到平稳状态。

下面通过一个简单的例子来验证吉布斯采样:假设我们掷两个骰子,用x表示第一个骰子的点数,y表示两个骰子点数之和.我们需要采样大量的(x,y)数据对(条件联合分布). 例子来源：《Data Science from Scratch》，Joel Grus.

# 均匀分布掷骰子
def roll_a_die():
    return random.choice([1,2,3,4,5,6])
# 直接采样二维分布
def direct_sample():
    x1=roll_a_die()
    x2=roll_a_die()
    return x1,x1+x2

# gibbs采样
def random_y_given_x(x):
    x2=roll_a_die()
    return x+x2 #已知x的条件下的y的分布
def random_x_given_y(y):
    if y<=7:
        return random.randrange(1,y) #1~6
    else:#8~12
        return random.randrange(y-6,7)
# 迭代过程中x,y的条件随机值互相替换
def gibbs_sample(num_iters=100):
    x,y=1,1 #任意有效都可作初始值
    for _ in range(num_iters):
        x=random_x_given_y(y)
        y=random_y_given_x(x)
    return x,y
# 与直接采样法做对比验证
def compare_distibutions(num_samples=1000):
    counts=defaultdict(lambda: [0,0])
    for _ in range(num_samples):
        counts[gibbs_sample()][0] += 1
        counts[direct_sample()][1] += 1
    return counts

Q：MCMC采样法如何得到相互独立的样本?

由于马尔科夫链的转移概率是条件概率，后一个样本依赖前一个样本，并非相互独立。可以采用多条马尔科夫链来生成样本，每条之间是相互独立的。或者在一条链上以较长的间隔取样本，能够得到近似独立的样本。

参考：

• 《LDA漫游指南》
• 随机采样方法整理与讲解（Acceptance-Rejection、MCMC、Gibbs Sampling等）
• MCMC(三)MCMC采样和M-H采样 - 刘建平Pinard

蓄水池抽样-流式均匀分布

Q：给出一个数据流，这个数据流的长度很大或者未知，并且对该数据流中数据只能访问一次。请给出一个随机选择算法，使得数据流中所有数据被选中的概率相等。

A：在处理数据流的过程中, 对第k个元素以1/k的概率决定是否替换已选中的元素(初始被选中的元素为空), 那么最后n个元素每个元素被选中的概率是1/n.

证明：由于每个元素被选中是独立事件，因此不需要关注前边元素的选中情况，只需关注是否被后边元素替换。

最终选中的元素是k的概率为：第k个元素被选中的概率x它后面的元素没有被选中的概率

\[{1\over k}\times {k\over k+1}\times {k+1\over k+2}\times\cdots\times{n-1\over n}={1\over n} \]

扩展，即如何从未知或者很大样本空间随机地取k个数？

类比下即可得到答案，即先把前k个数放入蓄水池，对第α个数，我们以 k/α 概率决定是否要把它换入蓄水池，换入时随机的选取一个作为替换项，这样一直做下去，对于任意的样本空间n，对每个数的选取概率都为k/n。也就是说对每个数选取概率相等。

问题: 对于 \(n(n>=k)\) 个元素, 遍历时如果每次以 \(\frac{k}{i}\) 的概率决定是否将它放入蓄水池，直到 \(n\), 那么最后每个元素被选中的概率相等, 即为 \(\frac{\mathrm{k}}{\mathrm{n}}\)

证明如下：

设某元素 \(\alpha\), 且 \(\alpha \leq \mathrm{n}\) 那么它最后被选中的概率是: 它被选中的概率 * [它后面的元素没有被选中+它后面的元素被选中*没有替换 \(\alpha\) ] ，即：

\[\begin{align} & \frac{\mathrm{k}}{\alpha} \times \left\{ \left(\frac{\alpha+1-\mathrm{k}}{\alpha+1}+\frac{\mathrm{k}}{\alpha+1} \times \frac{\mathrm{k}-1}{\mathrm{k}}\right) \times \left(\frac{\alpha+2-\mathrm{k}}{\alpha+2}+\frac{\mathrm{k}}{\alpha+2} \times \frac{\mathrm{k}-1}{\mathrm{k}}\right) \times \cdots \times \left(\frac{\mathrm{n}-\mathrm{k}}{\mathrm{n}}+\frac{\mathrm{k}}{\mathrm{n}} \times \frac{\mathrm{k}-1}{\mathrm{k}} \right) \right\} \\ =& \frac{\mathrm{k}}{\alpha} \times\left\{\frac{\alpha}{\alpha+1} \times \frac{\alpha+1}{\alpha+2} \times \cdots \times \frac{\mathrm{n}-1}{\mathrm{n}}\right\} = \frac{\mathrm{k}}{\alpha} \times \frac{\alpha}{\mathrm{n}}=\frac{\mathrm{k}}{\mathrm{n}} \end{align} \]