深度学习网络层之 Batch Normalization

Batch Normalization

S. Ioffe 和 C. Szegedy 在2015年《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》论文中提出此方法来减缓网络参数初始化的难处.

Batch Norm原理

内部协转移（Internal Covariate Shift）：由于训练时网络参数的改变导致的网络层输出结果分布的不同。这正是导致网络训练困难的原因。

对输入进行白化（whiten：0均值，单位标准差，并且decorrelate去相关）已被证明能够加速收敛速度，参考Efficient backprop. （LeCun et al.1998b）和 A convergence anal-ysis of log-linear training.（Wiesler & Ney,2011）。由于白化中去除相关性类似PCA等操作，在特征维度较高时计算复杂度较高，因此提出了两种简化方式：
1）对特征的每个维度进行标准化，忽略白化中的去除相关性；
2）在每个mini-batch中计算均值和方差来替代整体训练集的计算。

batch normalization中即使不对每层的输入进行去相关，也能加速收敛。通俗的理解是在网络的每一层的输入都先做标准化预处理(公式中k为通道channel数),再向整体数据的均值方差方向转换.

标准化: unit gaussian activations

\[\hat x^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{\operatorname{Var[x^{(k)}]}}} \]

Batch Normalizing Transform 转换式子:

\[\begin{align} \mu &= \frac{1}{m}\sum_{i=1}^m x_i &\text{//mini-batch mean} \\ \sigma^2 &= \frac{1}{m} \sum_{i=1}^m (x_i - \mu)^2 &\text{//mini-batch variance} \\ \hat{x_i} &= \frac{x_i - u}{\sqrt{\sigma^2 + \epsilon}} &\text{//normalize} \\ y_i &= \gamma \hat{x_i} + \beta &\text{//scale and shift} \end{align} \]

其中 ϵ 是为了防止方差为0导致数值计算的不稳定而添加的一个小数，如1e−6。

那么标准化为什么通常能够加速收敛?

角度1：损失函数。
以均方误差损失函数为例, 假设有两个特征x1, x2:

\[\begin{align} \mathcal{L}_{\bf w}(X,Y) =& \mathbb{E}_{{\bf x} \sim } \left[ \sum_{i=1}^N \left( y_i - {\bf w}^\top {\bf x}_i \right)^2 \right] \\ =& \mathbb{E}_{{\bf x} \sim } \left[ \sum_{i=1}^N y_i^2 - 2 y_i {\bf w}^\top {\bf x}_i + ( {\bf w}^\top {\bf x}_i )^2 \right] \\ =& \mathbb{E}_{{\bf x} \sim } \left[ \sum_{i=1}^N y_i^2 - 2 y_i (w_1 x_1 + w_2 x_2 ) + ( w_1 x_1 + w_2 x_2 )^2 \right] \\ =& \sum_{i=1}^N y_i^2 - 2 y_i w_1 \mathbb{E}_{x_1 \sim } \big[x_1 \big] - 2 y_i w_2 \mathbb{E}_{x_2 \sim } \big[ x_2 \big] \\ & + w_1^2 \mathbb{E}_{x_1 \sim } \big[ x_1^2 \big] + w_2^2 \mathbb{E}_{x_2 \sim } \big[ x_2^2 \big] + 2 w_1 w_2 \mathbb{E}_{ {\bf x} \sim } \big[ x_1 x_2 \big] \\ \end{align} \]

通过标准化, 使$X_1\sim N(0 ,1),X_2\sim N(0 ,1)$, 则有

\[\mathcal{L}_{\bf w}(X,Y) = \sum_{i=1}^N y_i^2 + w_1^2 \mathbb{E}_{x_1 \sim } \big[ x_1^2 \big] + w_2^2 \mathbb{E}_{x_2 \sim } \big[ x_2^2 \big] \\ \]

损失函数变为“对称”的二次函数，从而得到最优解的速度更快.

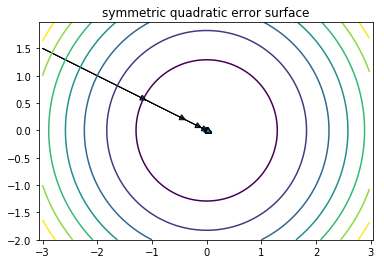
对称优化函数非对称

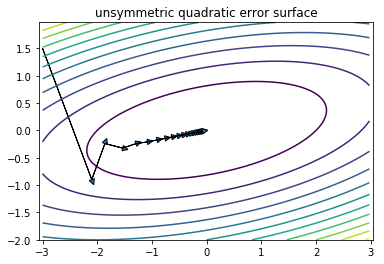
角度2：伸缩不变性。 ^[1]

权重伸缩不变性

权重伸缩不变性（weight scale invariance）指的是，当权重 $\mathbf W$ 按照常量 $\lambda$ 进行伸缩时 $\mathbf W'=\lambda \mathbf W$，得到的规范化后的值保持不变, $Norm(\mathbf{W'}\mathbf{x})=Norm(\mathbf{W}\mathbf{x})$ . 从而

\[\frac{\partial Norm(\mathbf{W'x})}{\partial \mathbf{W}} = \frac{\partial Norm(\mathbf{Wx})}{\partial \mathbf{W}} \]
因此，权重的伸缩变化不会影响反向梯度的 Jacobian 矩阵，因此也就对反向传播没有影响，避免了反向传播时因为权重过大或过小导致的梯度消失或梯度爆炸问题，从而加速了神经网络的训练。因此权重伸缩不变性可以有效地提高反向传播的效率。
数据伸缩不变性, 与权重不变性类似，输入数据发生伸缩变化时norm值不变。可以有效地减少梯度弥散，简化对学习率的选择。每一层神经元的输出依赖于底下各层的计算结果。如果没有正则化，当下层输入发生伸缩变化时，经过层层传递，可能会导致数据发生剧烈的膨胀或者弥散，从而也导致了反向计算时的梯度爆炸或梯度弥散。

Batch Norm特征转换scale

随着前边各层的累计影响,导致某一层的特征在非线性层的饱和区域,因此如果能对该特征做变换,使之处于较好的非线性区域,那么可使得信号传播更有效.假如将标准化的特征直接交给非线性激活函数,如sigmoid,则特征被限制在线性区域，这样改变了原始特征的分布。

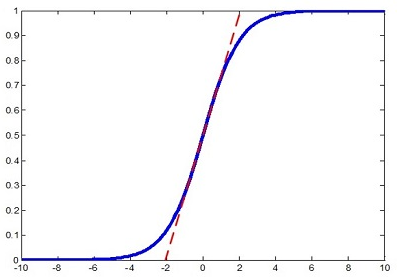
sigmoid-linear-part

论文中引入了两个可学习的参数$\gamma , \beta$来近似还原原始特征分布。这两个参数学习的目标是$\gamma=\sqrt{\text{Var}[X]}、 \beta=\mathbb E[X]$,其中$X$表示所有样本在该层的特征.原来的分布方差和均值由前层的各种参数weight耦合控制，而现在仅由$\gamma , \beta$控制，这样在保留BN层足够的学习能力的同时，使其学习更加容易。因此，加速收敛并非由于计算量减少（反而由于增加了参数增加了计算量）。

那么为什么要先normalize再通过$\gamma , \beta$线性变换来调整均值方差（甚至会恢复接近原来的样子），这不是多此一举吗？
在一定条件下可以纠正原始数据的分布（方差，均值变为新值γ,β），当原始数据分布足够好时就是恒等映射，不改变分布。如果不做BN，方差和均值对前面网络的参数有复杂的关联依赖，具有复杂的非线性。在新参数 γH′ + β 中仅由 γ,β 确定，与前边网络的参数无关，因此新参数很容易通过梯度下降来学习，能够学习到较好的分布。

反向传播

反向传播梯度计算如下：

\[\begin{aligned} \frac{\partial \ell}{\partial \widehat{x}_{i}} &=\frac{\partial \ell}{\partial y_{i}} \cdot \gamma \\ \frac{\partial \ell}{\partial \sigma_{\mathcal{B}}^{2}} &=\sum_{i=1}^{m} \frac{\partial \ell}{\partial \widehat{x}_{i}} \cdot\left(x_{i}-\mu_{\mathcal{B}}\right) \cdot \frac{-1}{2}\left(\sigma_{\mathcal{B}}^{2}+\epsilon\right)^{-3 / 2} \\ \frac{\partial \ell}{\partial \mu_{\mathcal{B}}} &=\left(\sum_{i=1}^{m} \frac{\partial \ell}{\partial \widehat{x}_{i}} \cdot \frac{-1}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}}\right)+\frac{\partial \ell}{\partial \sigma_{\mathcal{B}}^{2}} \cdot \frac{\sum_{i=1}^{m}-2\left(x_{i}-\mu_{\mathcal{B}}\right)}{m} \\ \frac{\partial \ell}{\partial x_{i}} &=\frac{\partial \ell}{\partial \widehat{x}_{i}} \cdot \frac{1}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}}+\frac{\partial \ell}{\partial \sigma_{\mathcal{B}}^{2}} \cdot \frac{2\left(x_{i}-\mu_{\mathcal{B}}\right)}{m}+\frac{\partial \ell}{\partial \mu_{\mathcal{B}}} \cdot \frac{1}{m} \\ \frac{\partial \ell}{\partial \gamma} &=\sum_{i=1}^{m} \frac{\partial \ell}{\partial y_{i}} \cdot \widehat{x}_{i} \\ \frac{\partial \ell}{\partial \beta} &=\sum_{i=1}^{m} \frac{\partial \ell}{\partial y_{i}} \end{aligned} \]

BN的前向与反向传播示意图:

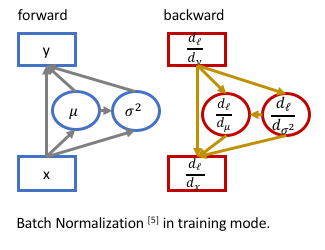
bn-forward-backward

在训练时计算mini-batch的均值和标准差并进行反向传播训练，而测试时并没有batch的概念，训练完毕后需要提供固定的 $\bar\mu,\bar\sigma$ 供测试时使用。论文中对所有的mini-batch的 $\mu_\mathcal B,\sigma^2_\mathcal B$ 取了均值(m是mini-batch的大小,$\bar\sigma^2$采用的是无偏估计)：

\[\begin{align} \bar\mu &=\mathbb E[\mu_\mathcal B] \\ \bar\sigma^2 &={m\over m-1}\mathbb E[\sigma^2_\mathcal B] \end{align} \]

每个mini-batch求$\bar\mu,\bar\sigma$这两个统计量时是对所有的特征点一起计算求的均值和方差.

测试阶段，同样要进行归一化和缩放平移操作，唯一不同之处是不计算均值和方差，而使用训练阶段记录下来的$\bar\mu,\bar\sigma$。

\[\begin{align} y&=γ({x-\bar\mu\over\sqrt{\bar\sigma^2+ϵ}})+ β \\ &={γ\over\sqrt{\bar\sigma^2+ϵ}}\cdot x+(β-{γ\bar\mu\over\sqrt{\bar\sigma^2+ϵ}}) \end{align} \]

一句话描述 Batch Norm: Batch Norm 是对数据归一化后再进行线性变换从而改善数据分布, 其中的线性变换参数是可学习的。神经网络中可以在多处使用Batch Norm层，对多层进行调节。

Batch Norm优点

减轻过拟合
改善梯度传播（权重不会过高或过低）
容许较高的学习率，能够提高训练速度。
减轻对初始化权重的强依赖，使得数据分布在激活函数的非饱和区域，一定程度上解决梯度消失问题。
作为一种正则化的方式，在某种程度上减少对dropout的使用。

Batch Norm层位置

在激活层（如 ReLU ）之前还是之后，没有一个统一的定论。在原论文中提出在非线性层之前（CONV_BN_RELU），比如 ResNet 中采用的conv -> BN -> ReLU，ResNetV2 预激活: BN -> ReLU -> conv 。在实际编程中也有人放在激活层之后(BN_CONV_RELU)。

Batch Norm 应用

Batch Norm在卷积层的应用

前边提到的mini-batch说的是神经元的个数，而卷积层中是堆叠的多个特征图，共享卷积参数。如果每个神经元使用一对$\gamma , \beta$参数，那么不仅多，而且冗余。可以在channel方向上取m个特征图作为mini-batch,对每一个特征图计算一对参数。这样减少了参数的数量。

应用举例-VGG16

为VGG16结构模型添加Batch Normalization。

重新完全训练.如果想将BN添加到卷基层，通常要重新训练整个模型，大概花费一周时间。
finetune.只将BN添加到最后的几层全连接层，这样可以在训练好的VGG16模型上进行微调。采用ImageNet的全部或部分数据按batch计算均值和方差作为BN的初始$\beta,\gamma$参数。

与 Dropout 合作

Batch Norm的提出使得dropout的使用减少,但是Batch Norm不能完全取代dropout,保留较小的dropout率,如0.2可能效果更佳。

Batch Norm 实现

Caffe框架的BatchNorm层参数设置示例:

layer {
    name: "conv1/bn"
    type: "BatchNorm"
    bottom: "conv1"
    top: "conv1"
    param { lr_mult: 0 decay_mult: 0 } # mean
    param { lr_mult: 0 decay_mult: 0 } # var
    param { lr_mult: 0 decay_mult: 0 } # scale
    batch_norm_param { use_global_stats: true } # 训练时设置为 false
}

Caffe框架中 BN 层全局均值和方差的实现：

与论文计算 global 均值和 global 方差的方式不同之处在于，Caffe 中的 global 均值和 global 方差采用的是滑动衰减平均的更新方式，设滑动衰减系数moving_average_fraction 为 λ，当前的 mini-batch 的均值和方差分别为 $\mu_B,\sigma_B^2$，则滑动更新公式为：

\[\begin{align} \mu_{new} &= (\lambda \mu_{old} + \mu_B) / s \\ \sigma_{new}^2 &= \begin{cases} (\lambda \sigma_{old}^2 + \frac{m - 1}{m} \sigma_B^2)/s & m > 1 \\ (\lambda \sigma_{old}^2 + \sigma_B^2)/s & m = 1 \end{cases} \\ s &= \lambda s+1 \end{align} \]

简化形式表示为:$ S_t = (1-\lambda)Y_t + \lambda \cdot S_{t-1} $.
式子中存在一个缩放因子 s 代替 batch size(或者说滑动步长), $\mu_B,\sigma_B^2, s$ 初始化为 0, 未采用求训练集所有样本的平均均值和无偏估计方差的原因是计算不便,需要节约内存和计算资源.

在何凯明的caffe实现中仅给出了deploy.prototxt文件方便测试和finetuning.在deploy.prototxt中batch norm层的参数被freeze固定住了,其均值和方差是在大量数据上严格按照论文中的average方法而不是caffe实现中的moving average方法得到的,数值比较稳定.
caffe中的batch_norm_layer仅含均值方差,不包括gamma/beta,需要后边紧跟scale_layer,并使用bias来分别对应gamma、beta因子，用于自动学习缩放参数。

caffe实现的batch_norm_layer.cpp代码如下:

// scale初始化代码: 用三个blob记录BatchNorm层的三个数据
void BatchNormLayer<Dtype>::LayerSetUp(...) {
    vector<int> sz;
    sz.push_back(channels_);
    this->blobs_[0].reset(new Blob<Dtype>(sz)); // mean
    this->blobs_[1].reset(new Blob<Dtype>(sz)); // variance
    // 在caffe实现中计算均值方差采用了滑动衰减方式, 用了scale_factor代替num_bn_samples(scale_factor初始为1, 以s=λs + 1递增).
    sz[0] = 1;
    this->blobs_[2].reset(new Blob<Dtype>(sz)); // normalization factor (for moving average)
}

if (use_global_stats_) {
    // use the stored mean/variance estimates.
    const Dtype scale_factor = this->blobs_[2]->cpu_data()[0] == 0 ?
        0 : 1 / this->blobs_[2]->cpu_data()[0];
    caffe_cpu_scale(variance_.count(), scale_factor,
        this->blobs_[0]->cpu_data(), mean_.mutable_cpu_data());
    caffe_cpu_scale(variance_.count(), scale_factor,
        this->blobs_[1]->cpu_data(), variance_.mutable_cpu_data());
} else {
    // compute mean
    caffe_cpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
        1. / (num * spatial_dim), bottom_data,
        spatial_sum_multiplier_.cpu_data(), 0.,
        num_by_chans_.mutable_cpu_data());
    caffe_cpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
        num_by_chans_.cpu_data(), batch_sum_multiplier_.cpu_data(), 0.,
        mean_.mutable_cpu_data());
  }

  // subtract mean
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
      batch_sum_multiplier_.cpu_data(), mean_.cpu_data(), 0.,
      num_by_chans_.mutable_cpu_data());
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
      spatial_dim, 1, -1, num_by_chans_.cpu_data(),
      spatial_sum_multiplier_.cpu_data(), 1., top_data);

  if (!use_global_stats_) {
    // compute variance using var(X) = E((X-EX)^2)
    caffe_powx(top[0]->count(), top_data, Dtype(2),
        temp_.mutable_cpu_data());  // (X-EX)^2
    caffe_cpu_gemv<Dtype>(CblasNoTrans, channels_ * num, spatial_dim,
        1. / (num * spatial_dim), temp_.cpu_data(),
        spatial_sum_multiplier_.cpu_data(), 0.,
        num_by_chans_.mutable_cpu_data());
    caffe_cpu_gemv<Dtype>(CblasTrans, num, channels_, 1.,
        num_by_chans_.cpu_data(), batch_sum_multiplier_.cpu_data(), 0.,
        variance_.mutable_cpu_data());  // E((X_EX)^2)

    // compute and save moving average
    this->blobs_[2]->mutable_cpu_data()[0] *= moving_average_fraction_;
    this->blobs_[2]->mutable_cpu_data()[0] += 1;
    caffe_cpu_axpby(mean_.count(), Dtype(1), mean_.cpu_data(),
        moving_average_fraction_, this->blobs_[0]->mutable_cpu_data());
    int m = bottom[0]->count()/channels_;
    Dtype bias_correction_factor = m > 1 ? Dtype(m)/(m-1) : 1;
    caffe_cpu_axpby(variance_.count(), bias_correction_factor,
        variance_.cpu_data(), moving_average_fraction_,
        this->blobs_[1]->mutable_cpu_data());
  }

  // normalize variance
  caffe_add_scalar(variance_.count(), eps_, variance_.mutable_cpu_data());
  caffe_powx(variance_.count(), variance_.cpu_data(), Dtype(0.5),
             variance_.mutable_cpu_data());

  // replicate variance to input size
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, num, channels_, 1, 1,
      batch_sum_multiplier_.cpu_data(), variance_.cpu_data(), 0.,
      num_by_chans_.mutable_cpu_data());
  caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels_ * num,
      spatial_dim, 1, 1., num_by_chans_.cpu_data(),
      spatial_sum_multiplier_.cpu_data(), 0., temp_.mutable_cpu_data());
  caffe_div(temp_.count(), top_data, temp_.cpu_data(), top_data);
  
  caffe_copy(x_norm_.count(), top_data,
      x_norm_.mutable_cpu_data());

BN有合并式和分离式，各有优劣。^[2]

分离式写法，在切换层传播时，OS需要执行多个函数，在底层（比如栈）调度上会浪费一点时间。Caffe master branch当前采用的是分离式写法，CONV层扔掉bias，接一个BN层，再接一个带bias的SCALE层。
从执行速度来看，合并式写法需要多算一步bias，参考这里的合并式写法。

BatchNorm层合并(Conv+BN+Scale+ReLU => Conv+ReLU)

内存优化

因为Conv、BN、Scale都是线性变换，因此可以合并为一个变换。
在训练时可以将bn层合并到scale层,在测试(inference)时可以把bn和scale合并到conv层. 在训练时也可以将冻结的BN层合并到冻结的conv层, 但是不能训练合并后的conv层, 否则会破坏bn的参数. 合并 bn 层同时可以减少一点计算量.

仅合并BN+Scale=>Scale

bn layer: bn_mean, bn_variance, num_bn_samples 注意在caffe实现中计算均值方差采用了滑动衰减方式,用了scale_factor代替num_bn_samples(scale_factor初始为1,以s=λs+1递增).
scale layer: scale_weight, scale_bias 代表gamma,beta
BN层的batch的均值mu=bn_mean/num_bn_samples,方差var=bn_variance / num_bn_samples.
scale层设置新的仿射变换参数:

new_gamma = gamma / (np.power(var, 0.5) + 1e-5)
new_beta = beta - gamma * mu / (np.power(var, 0.5) + 1e-5)

Conv+BN+Scale=>Conv

conv layer: conv_weight, conv_bias
在使用BatchNorm时conv_bias通常为0
定义alpha向量为每个卷积核的缩放倍数(长度为通道数),也是特征的均值和方差的缩放因子.

alpha = scale_weight / sqrt(bn_variance / num_bn_samples + eps)
conv_bias = conv_bias * alpha + (scale_bias - (bn_mean / num_bn_samples) * alpha)
for i in range(len(alpha)): conv_weight[i] = conv_weight[i] * alpha[i]

Batch Norm 多卡同步

为什么不进行多卡同步?

早期的各框架中实现的BatchNorm都是只考虑了single gpu。也就是说BN使用的均值和标准差是单个gpu算的，相当于缩小了mini－batch size，而不是采用全局数据去计算均值方差。至于为什么这样实现，1）因为没有sync的需求，因为对于大多数vision问题，单gpu上的mini-batch已经够大了，对结果影响较小。2）影响训练速度，BN layer通常是在网络结构里面广泛使用的，每次调用时都同步一下所有GPU的数据，十分影响训练速度。^[3]

但是为了达到更好的效果, 实现Sync-BN也是很有意义的.

在深度学习平台框架中多数是采用数据并行的方式, 每个GPU卡上的中间数据没有关联.
为了实现跨卡同步BN, 在前向运算的时候需要计算全局的均值和方差，在后向运算时候计算全局梯度。最简单的实现方法是先同步求均值，再发回各卡然后同步求方差，但是这样就同步了两次。实际上均值和方差可以放到一起求解, 只需要同步一次就可以. 数据并行的方式改为下图所示:^[4]

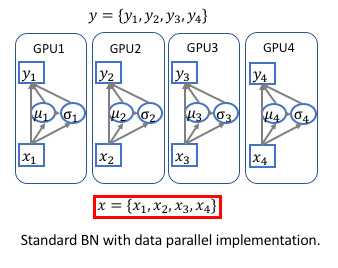
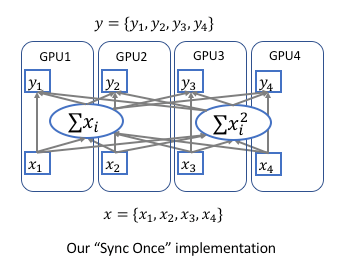
bn-data-parallel sync-bn

多卡同步的公式原理^[5]

\[\begin{align} \mu &= \frac{1}{m}\sum_{i=1}^m x_i \\ \sigma^2 &= \frac{1}{m} \sum_{i=1}^m (x_i - \mu)^2 = \frac{1}{m} \sum_{i=1}^m (x_i^2+\mu^2-2x_i\mu) = \frac{1}{m} \sum_{i=1}^m x_i^2 - \mu^2 \\ &= \frac{1}{m} \sum_{i=1}^m x_i^2 - (\frac{1}{m}\sum_{i=1}^m x_i)^2 \end{align} \]

因此总体batch_size对应的均值和方差可以通过每张GPU中计算得到的 $\sum x_i$ 和 $\sum x_i^2$ reduce相加得到. 在反向传播时也一样需要同步一次梯度信息.

另外, 可以参考sync-bn 实现讨论.

posted @ 2017-09-22 19:55 康行天下阅读(17584) 评论(11) 编辑收藏举报

刷新页面返回顶部

明也无涯

不积跬步无以至千里