深度学习-conv卷积

卷积

卷积是一种定义在两个函数($f$ 和 $g$)上的数学操作，旨在产生一个新的函数。$f$ 和 $g$ 的卷积可以写成 $f\ast g$，数学定义如下：

$$\begin{array}{}\text{(连续形式)}& (f\ast g)(t)& ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(\tau )g(t-\tau )\text{(离散形式)}& (f\ast g)(t)& ={\sum }_{\tau =-\mathrm{\infty }}^{\mathrm{\infty }}f(\tau )g(t-\tau )\end{array}$$

举例说明：掷骰子问题^[1]

假设有两个骰子，两个骰子分别是$f$ 和 $g$，$f(1)$ 表示骰子 $f$ 向上一面为数字1的概率。同时抛掷这两个骰子1次，它们正面朝上数字和为4的概率是多少？很容易想出有三种情况，分别是：

• $f$ 向上为1，$g$ 向上为3；
• $f$ 向上为2，$g$ 向上为2；
• $f$ 向上为3，$g$ 向上为1；

这三种情况出现的概率和即问题的答案，如果写成公式就是 $(f\ast g)(4)=\sum _{\tau =1}^{3}f(\tau )g(4-\tau )$。

写成内积的形式为：$[...,f(1),f(2),f(3),...]\cdot [...,g(3),g(2),g(1),...]$ ，
可以看出卷积其实就是把一个函数的输入卷(翻)过来，与另一个函数求内积。

对应到不同方面，卷积可以有不同的解释：$g$ 既可以看作我们在深度学习里常说的核(Kernel)，也可以对应到信号处理中的滤波器(Filter)。而 $f$ 可以是我们所说的机器学习中的特征(Feature)，也可以是信号处理中的信号(Signal)。卷积 ($f\ast g$) 就可以看作是对 $f$ 的加权求和。^[2]

图像滤波器

传统的图像过滤器算子有以下几种:

• blur kernel：减少相邻像素的差异，使图像变平滑。
• sobel：显示相邻元素在特定方向上的差异。
• sharpen ：强化相邻像素的差异，使图片看起来更生动。
• outline：也称为edge kernel，相邻像素相似亮度的像素点设成黑，有较大差异的设为白。

更多可参考 image-kernels 在线演示不同的卷积过滤器。

CNN 卷积层

CNN做的事情不是提前决定好过滤器，而是把过滤器当成参数不断调整学习，学出合适的过滤器。卷积网络的第一层执行的通常都是边缘检测，后面的层得到的都是更抽象的特征。CNN 的卷积核可以看作是局部区域内的全连接. 卷积层的一个重要特性是权值共享.

权值共享: 不同的感受域共享同一权值,因此也称为filter,能够大大减少权重的数量(所占的内存),这通常是有效的,因为filter过滤某一特征与具体的空间位置无关.但无独有偶,人脸图片通常是中心化的,即人的脑袋比较靠近中间,如此可以看出位置信息是有用的.对于这种情形我们可以取消权值共享机制,此时称这一层为Locally-Connected Layer.这在人脸识别的论文中比较常用.

参数量: C_in × C_out × kernel_h × kernel_w

误区: 我之前误认为卷积的参数量是 C_out × kernel_h × kernel_w, 如果将卷积层设计为输入的所有channel的特征图共享一个filter, 那么相当于将输入的channel压缩成1个(特征图相加)再与C_out个filter卷积. 这种方式参数量和计算量比较小,但网络性能可能较低.

有时候提到filter的长和宽大小而不提到深度,则深度是输入数据的整个深度(因此1x1的卷积核也是有意义的).如前一层的输入是 [16x16x20],感知域大小是3x3,那么卷积层中每个神经元将有3x3x20 = 180个到前一层的连接.

小卷积核

现在流行的网络结构设计多遵循小卷积核的设计原则, 小卷积核的优势:
3个3x3的卷积核的累加相当于1个7x7的卷积核,但是参数更少,计算量更小,有更多的非线性层计算.还可以通过加入1x1的"bottleneck"卷积核进一步减少计算(GoogLeNet等大量运用这种方式加深层次).如输入HxWxC经过下列步骤输出的维数不变:

$$\begin{array}{ccc}H\times W\times C& \stackrel{\text{Conv 1x1 x C/2}}{\to }& H\times W\times C/2\\ & & \text{Conv 3x3 x C/2}\downarrow & \\ H\times W\times C& \stackrel{\text{Conv 1x1 x C}}{\leftarrow }& H\times W\times C/2\end{array}$$

然而上述步骤中仍然使用了3x3卷积核,可以将其转成1x3与3x1的连接.

输入输出尺度关系：

$$o=\lfloor \frac{i+2p-k}{s}\rfloor +1$$

孔洞卷积/膨胀卷积

deeplab 论文 Rethinking Atrous Convolution for Semantic Image Segmentation 中提到 "Atrous convolution, also known as dilated convolution".

Dilated/Atrous Convolution 或者是 Convolution with holes 从字面上就很好理解，是在标准的 convolution 中注入空洞，以此来增加感受野。相比没有孔洞的卷积，dilated convolution 多了一个 dilation rate 超参数, 指的是 kernel 的间隙(无孔洞的卷积 dilation rate 是 1)。

http://ww3.sinaimg.cn/large/87c01ec7gy1fqxx2ni45xg20az0al0vu.gif

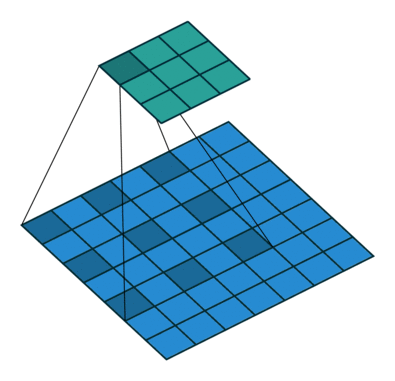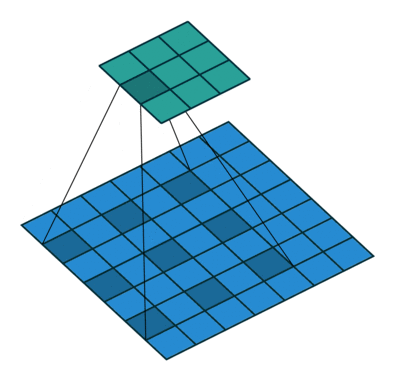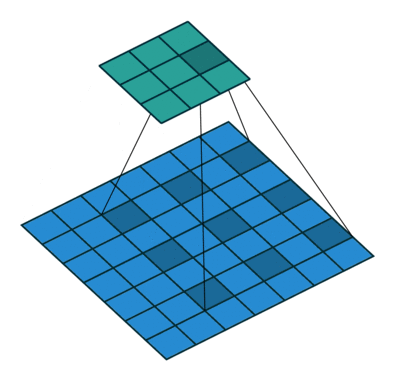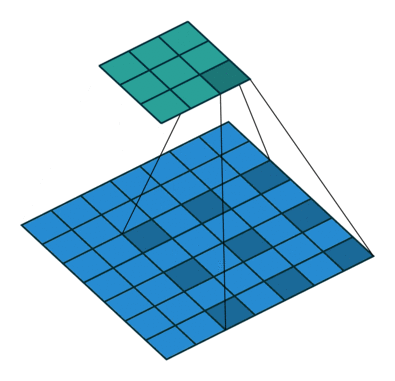
孔洞卷积输入输出尺度关系：

$$o=\lfloor \frac{i+2p-[(k-1)d+1]}{s}\rfloor +1$$

d是 dilation rate, 在kernel中加入了d-1个孔,相当于扩大了卷积核的覆盖面积,k'=k+(k-1)(d-1).

孔洞卷积应用

在 R-FCN 和 SSD 等目标检测网络中也用到了 atrous conv, R-FCN 将原本的ImageNet的预训练模型的某层stride=2的卷积改为stride=1使得输出尺度不进行缩小,由于stride=1的感受野较小,因此使用atrous来增大感受野. 同时能够继续使用ImageNet预训练分类模型.SSD将全连接层fc6和fc7改成了卷积层,并从fc6和fc7参数中下采样.将pool5从2x2-s2改成3x3-s1,同样使用atrous conv来填充孔洞,增加感受野.

atrous conv 能够使用原来的参数初始化是因为 atrous conv 的神经元连接和原来的仍然一样,如下图所示^[3], 红色的输出神经元对应的输入(第一层)的神经元在(a)(b)中相同:

atrous conv

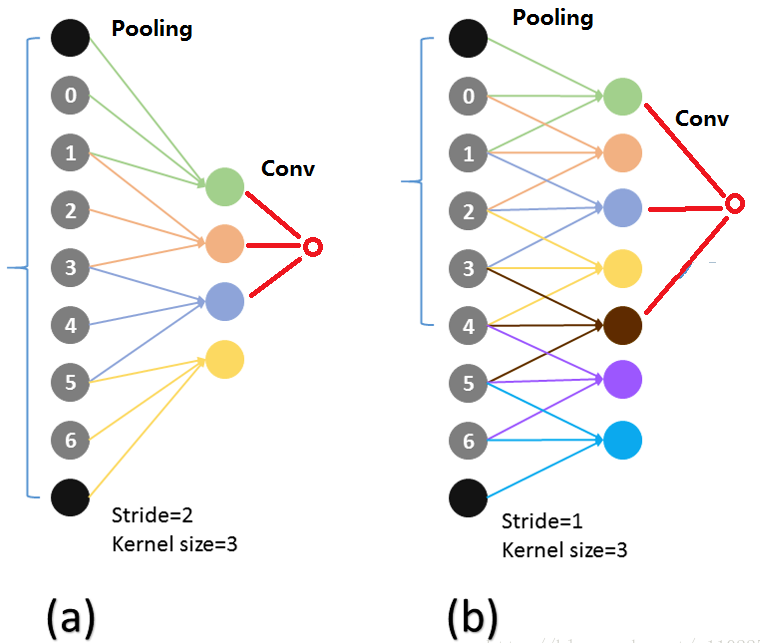
卷积实现

卷积有三种主流的计算方式：转化为矩阵乘，winograd，和FFT。

三种计算方式在 CuDNN 中均做了实现^[4]

CuDNN-Conv

在现代的 DL 框架中对卷积计算通常采用矩阵乘法的方式,使用im2col操作将输入数据与权重展开成二维矩阵(使得图像矩阵和卷积核能够直接相乘, 转换的反向操作为col2im),运用 BLAS API进行高效计算,缺点是占用许多内存.这种思想也可以用在pooling操作中.

没有广泛使用FFT的原因:
FFT 在卷积核比较大的时候有明显速度优势, 但是FFT卷积没有被广泛应用。因为通用平台上有更合适的Winograd卷积的存在，而专用平台上直接降低运算精度是更合适的方案。而且，随着CNN里面越来越多的1×1卷积和depthwise卷积被加入，Winograd卷积的价值也越来越小了。CNN的卷积核一般都小于5，所以深度学习中一般不用FFT。^[5]

下边简单介绍下快速傅里叶变换.

卷积定理(convolution theorem) ^[6][7]

快速傅里叶变换被称为20世纪最重要的算法之一, 一个因素就是卷积定理.
傅里叶变换可以看作是对图像或者音频等数据的重新组织,它将时域和空域上的复杂卷积对应到了频域中的元素间简单的乘积。
一维连续域上两个连续函数的卷积:

$$h(x)=f⨂g={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x-u)g(u)du={\mathcal{F}}^{-1}(\sqrt{2\pi }\mathcal{F}[f]\mathcal{F}[g])$$

由卷积定理可以知道,两个矩阵卷积的结果等价于两个矩阵经过傅里叶变换($\mathcal{F}$),进行元素级别相乘,再经过傅里叶逆变换(${\mathcal{F}}^{-1}$). $\sqrt{2\pi }$是一个normalizer.

二维离散域（图像）上的卷积:

$$\begin{array}{}\text{(1)}& \text{feature map}=& \text{intput}⨂\text{kernel}\text{(2)}& =& \sum _{y=0}^M\sum _{x=0}^N\text{intput}(x-a,y-b)\cdot \text{kernel}(x,y)\text{(3)}& =& {\mathcal{F}}^{-1}(\sqrt{2\pi }\mathcal{F}[\text{intput}]\mathcal{F}[\text{kernel}])\end{array}$$

快速傅里叶变换是一种将时域和空域中的数据转换到频域上去的算法。傅里叶变换用一些正弦和余弦波的和来表示原函数。必须注意的是，傅里叶变换一般涉及到复数，也就是说一个实数被变换为一个具有实部和虚部的复数。通常虚部只在一部分领域有用，比如将频域变换回到时域和空域上.

傅里叶变换图示^[8]

http://wx4.sinaimg.cn/large/006Fmjmcly1fdwm3am0yag30dw0b4tji.gif

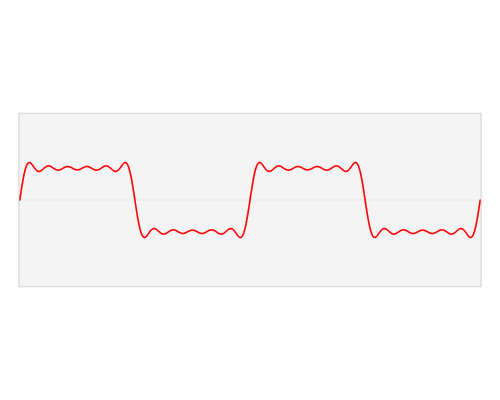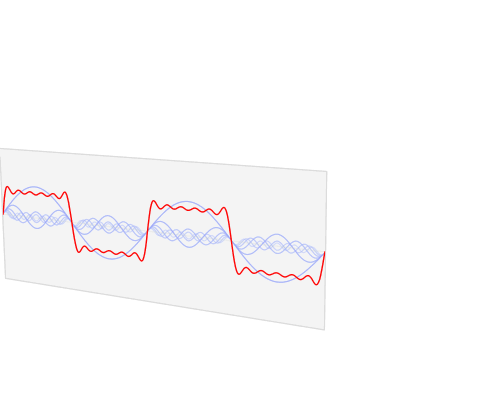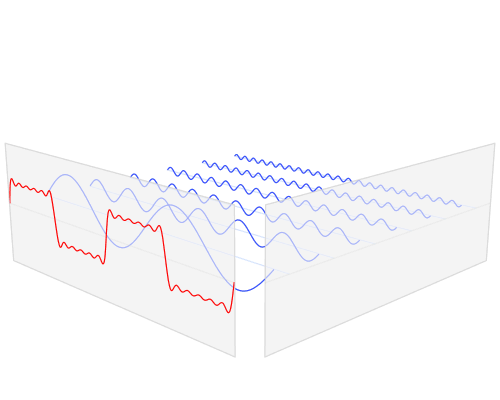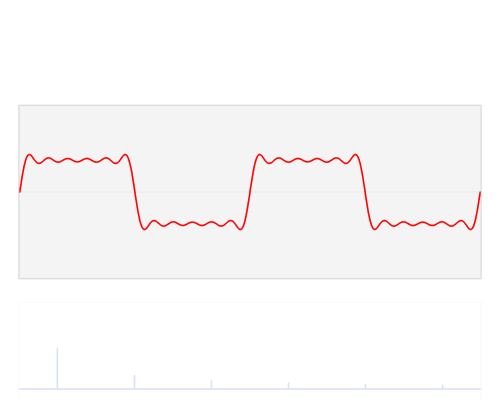
从傅里叶变换中可以看出方向信息:

Images by Fisher & Koryllos (1998). Source

FFT-orientation

Caffe 框架中的卷积实现

卷积操作示意图如下，输入图片的维数为[c0,h0,w0]；卷积核的维数为[c1,c0,hk,wk]，其中c0在图中没有表示出来，一个卷积核可以看成由c1个维数为[c0,hk,wk]的三维滤波器组成,输出特征的维数为[c1,h1,w1], 其中(h1,w1)根据输入尺寸(h0,w0)及卷积核尺寸(hk,wk),卷积核步长stride计算得出.

conv

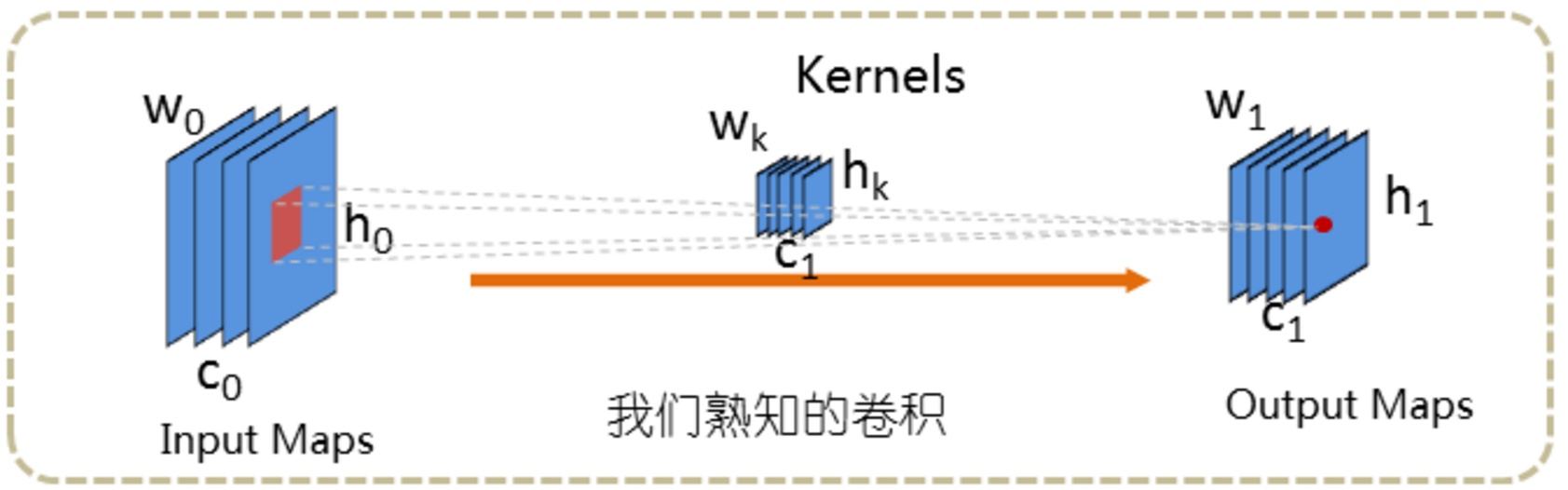
转成二维矩阵乘法的高效计算：

im2col

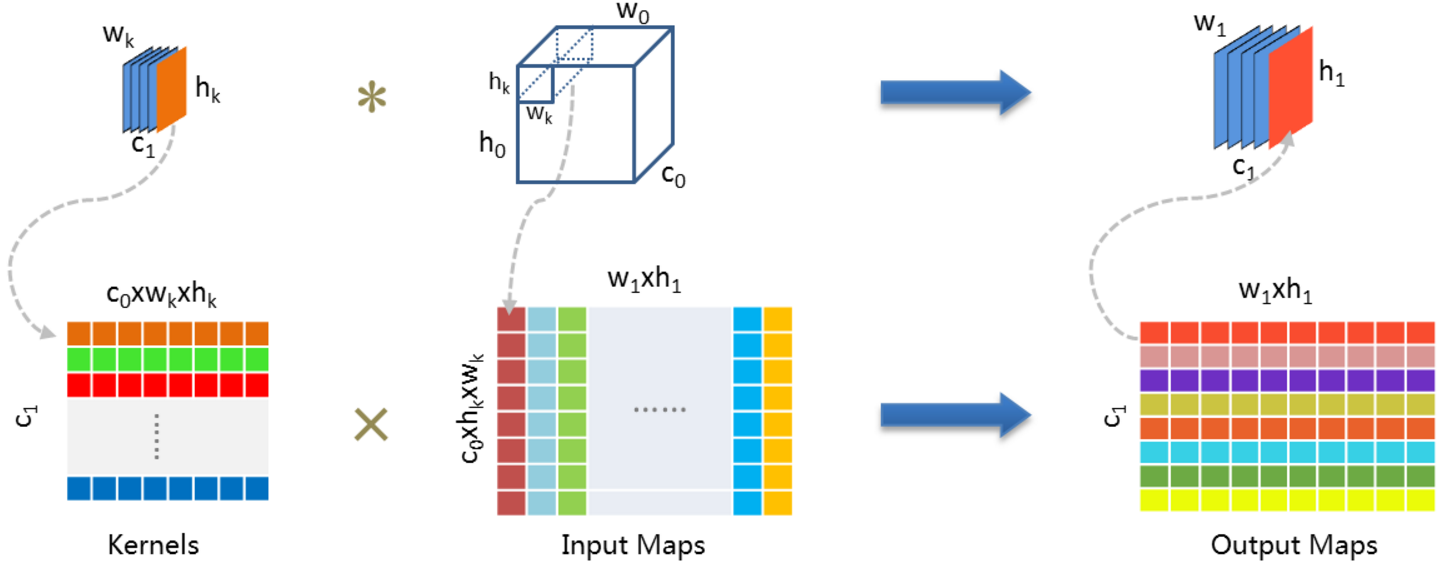
更详细的im2col图示：

im2col-detail

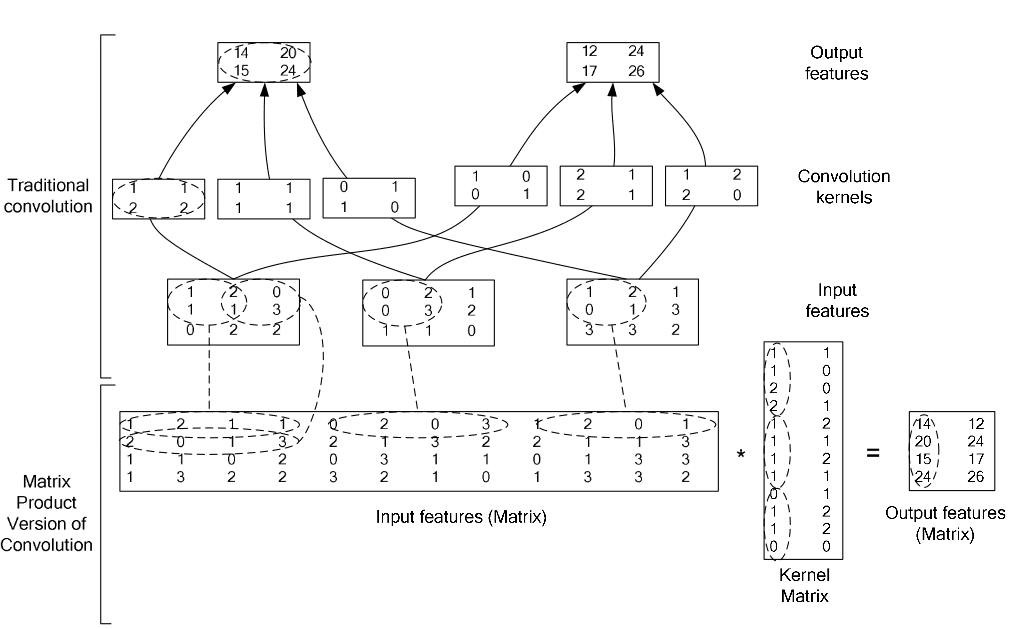
卷积-反向传播

卷积层的反向传播依然可以用到卷积.^[9]
设卷积层为 $Y=X\odot W$, im2col 的形式是 $Y=X^{\prime }\odot W^{\prime }$ , 那么

$$\begin{array}{}\text{(4)}& \frac{\partial L}{\partial W}& =X\odot \frac{\partial L}{\partial Y}\text{(5)}& \frac{\partial L}{\partial X}& =\mathrm{F}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}({180}^{\circ }\text{rotated W},\frac{\partial \mathrm{L}}{\partial \mathrm{Y}})\text{(6)}& \frac{\partial L}{\partial X^{\prime }}& =\frac{\partial L}{\partial Y}\odot W^{\prime }\text{(7)}& \frac{\partial L}{\partial X}& =\text{col2im}(\frac{\partial L}{\partial X^{\prime }})\end{array}$$

---

1. 如何通俗易懂地解释卷积 ↩︎

2. 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (一) ↩︎

3. 孔洞卷积: https://blog.csdn.net/z1102252970/article/details/70548412 ↩︎

4. http://www.telesens.co/2018/04/09/initializing-weights-for-the-convolutional-and-fully-connected-layers/ ↩︎

5. https://www.zhihu.com/question/264307400 ↩︎

6. http://www.hankcs.com/ml/understanding-the-convolution-in-deep-learning.html ↩︎

7. http://timdettmers.com/2015/03/26/convolution-deep-learning/ ↩︎

8. http://commons.wikimedia.org/wiki/File:Fourier_transform_time_and_frequency_domains.gif ↩︎

9. https://medium.com/@pavisj/convolutions-and-backpropagations-46026a8f5d2c ↩︎