Games202笔记：实时阴影（RTR Shadow）

目录

• 回顾
  • 渲染方程
  • 环境光
  • 全局光照
• 阴影贴图
  • 概念
  • 具体做法
  • 问题
    • 自遮挡
    • 锯齿（Aliasing）
  • 实时渲染中的数学
    • 近似相等
    • 实时渲染方程的近似相等
• 软阴影
  • 基本概念
  • PCF
  • PCF效果图
  • PCSS
    • 确定filter size
    • PCSS算法步骤
  • VSSM
  • MIPMAP
  • SAT
  • Moment Shadow Mapping
  • Distance Field Soft Shadows
    • SDF的使用
• 小结
• 参考

回顾

渲染方程

渲染方程（Rendering Equation）描述光传输的核心公式. 本质是能量守恒的积分方程，描述了一个点在某个方向上的出射辐射度（Radiance）是来自场景中所有其他方向的入射光的加权平均，同时考虑材料表面的反射特性.

标准形式：

\[L_o(p,ω_o)=L_e(p,ω_o)+\int_{H^2}f_r(p,ω_i\to ω_o)L_i(p,ω_i)cosθ_idω_i \]

• \(L_o(p,ω_o)\)：点p在\(ω_o\)方向上的出射辐射度（outgoing radiance）；
• \(L_e(p,ω_o)\)：点p在\(ω_o\)方向上的自发辐射（emission）；
• \(f_r(p,ω_i\to ω_o)\)：BRDF（双向反射分布函数），描述表面从入射方向\(ω_i\)到出射方向\(ω_o\)的反射特性；
• \(L_i(p,ω_i)\)：点p在\(ω_i\)方向上的入射辐射度（incident radiance from source）；
• \(cos θ_i\)：值为\(ω_i\cdot \bm{n}\)，\(θ_i\)是方向\(ω_i\)与p点法向量\(\bm{n}\)的夹角；
• \(H^2\)：p为球心的单位半球面上所有的入射方向.

实时渲染（Real-time rendering, RTR）

1）经常会考虑可见性（Visibility）
2）BRDF常与\(cos θ_i\)一起考虑

于是，RTR渲染方程：

\[L_o(p,ω_o)=\int_{Ω^+}[L_i(p,ω_i)][f_r(p,ω_i\to ω_o)cosθ_i][V(p,ω_i)]dω_i \]

注：未考虑自发光.

与普通渲染方程不同点：

• \(f_r(p,ω_i\to ω_o)cosθ_i\)：cos加权的BRDF（cosine-weighted BRDF），常放一起考虑；
• \(V(p,ω_i)\)：可见性（Visibility），光源发出的光和visibility结合一起，才是到达p点的incident lighting（入射光）；而有些点被遮挡，则无需考虑；
• Ω：单位球面半球（以法线方向为中心）上的所有入射方向.

渲染方程推导过程，参见：计算机图形：辐射度光照模型

环境光

环境光（Environment Lighting）指来自各个方向的入射光照. 典型实现技术：

1）立方体贴图（cube map），或球体贴图（sphere map）；

全局光照

全局光照 = 直接光照 + 间接光照

直接光照（Direct illumination）：光线只弹射1次；

间接光照（One-bounce global illumination）：光线弹射2次（及以上）.

阴影贴图

概念

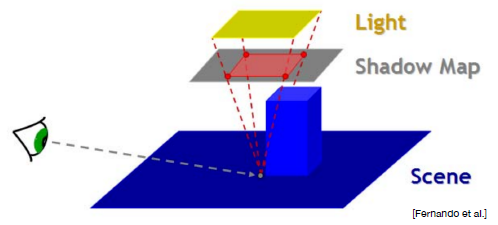
阴影贴图（Shadow Mapping, SM）是一个2趟算法（2-Pass Algorithm），即渲染场景2遍：

1）light pass: 从light出发看向场景，输出light能看到的场景深度，得到距离光源最近的深度，即SM对应的"depth buffer".

2）camera pass: 从camera位置出发，利用SM渲染整个场景.

优点（Pro）：无需知道场景的几何结构；
缺点（Con）：可能导致自遮挡和锯齿问题；

早期离线渲染，常用阴影贴图实现阴影，现在可用光线追踪.

具体做法

第一趟（Pass 1）：从光源位置看向场景，输出深度图（depth texture），描述距离光源最近点距离.

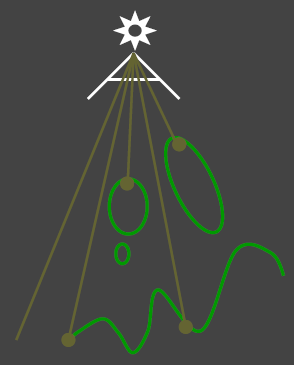
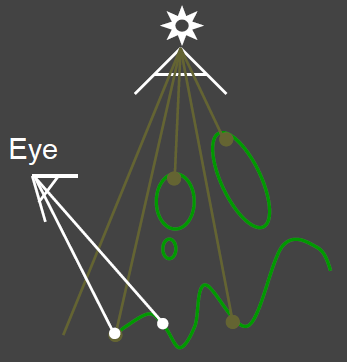
第二趟（Pass 2）：从眼睛/相机位置看向场景，对每个片元（fragment，也是着色点shading point），都用深度图判断物体是否能被Pass 1中光源所照到，如果不能被照到，说明在阴影里.

如下图，眼睛观察到物品表面上2个点，其中一个在阴影里，称为Blocked；另一个不在，称为Visible.

下图是点光源下，有阴影和无阴影的效果图对比：

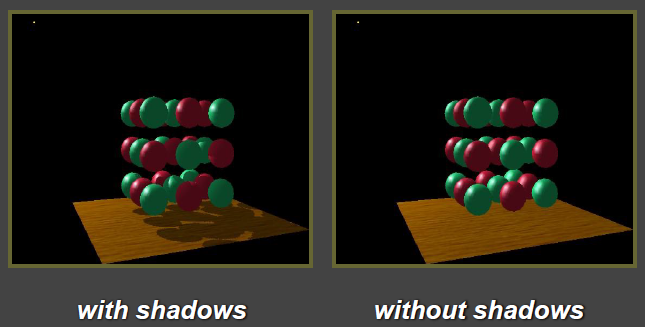
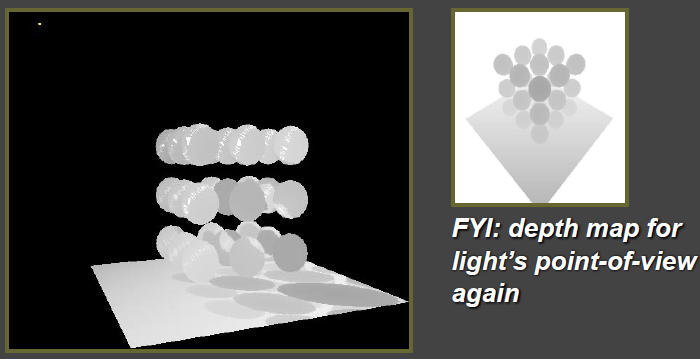
从光源视角看，深度图如下所示：

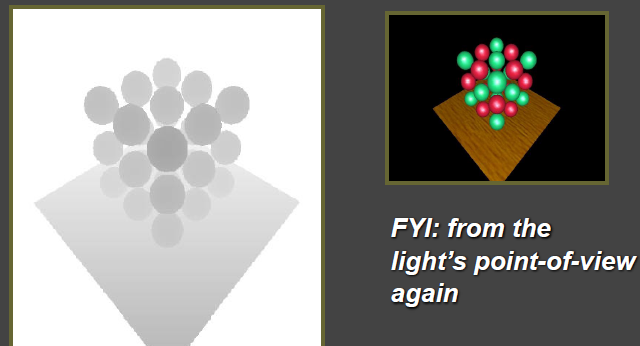
如果将深度图投影到眼睛的视图：

问题

自遮挡

阴影贴图存在自遮挡（self occulusion）问题.

如下图所示，

这是因为数值精度. 从光源角度看，深度图上记录的每个像素深度，在场景中目标位置对应一个小的区域（该区域垂直于光源到像素的观察方向）.

也就是说，在Shadow Maps看来，场景是离散成一个个小区域的（下图红色区域），而并非是平面（下图底部黑色）.

当眼睛观察到物体表面第n区域（实际深度）时，由于Shadow Maps的深度图是离散的，在光源看来，是第n-1区域对应深度（记录深度，比实际深度小）. 这样，第n区域就被第n-1区域遮挡，形成自遮挡现象.

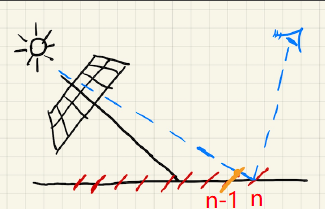
什么时候会发生自遮挡现象？

当光线方向与物体表面垂直时，自遮挡现象不明显；
当光线方向与物体表面几乎平行时，自遮挡最严重.

如何解决自遮挡问题？

可以为区域设置一个bias作为容忍区间，降低自遮挡现象. 具体来说，
当沿着到光源的方向，实际深度 ~ 实际深度+bias 之间，还存在障碍物时，不算遮挡. 这样，眼睛看到的实际深度（第n区域），就不会被记录成第n-1区域.

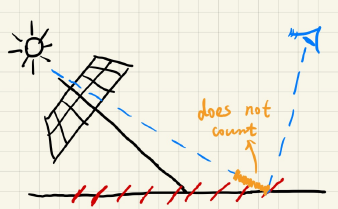
但是，又会带来新问题detached shadow，如下图所示，当bias过大时，人物阴影与脚断开了.

目前，工业界还没有真正解决该问题的办法，只是找一个合适的bias，使得渲染结果既不存在自遮挡，又不存在detached shadow问题.

学术界提出了一些解决方法.

• 第二深度阴影贴图（second-depth shadow mapping）

SM中，不仅记录最小深度，还记录第二小深度（次小深度）. 当进行深度比较时，用最小深度和第二小深度的平均值（midpoint）与片元深度比较.

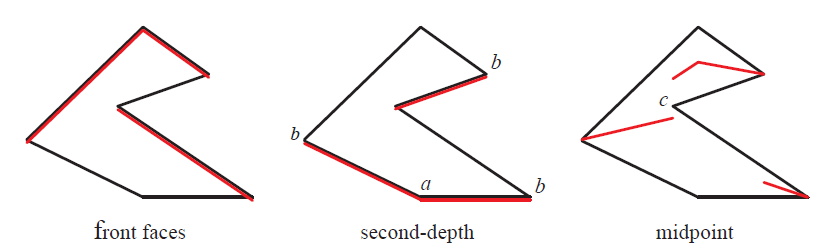
如下图是一个鞋子模型，光线垂直向下.

front faces: 是最小深度对应表面示意图；
second-depth：是次小深度对应表面示意图；
midpoint：是二者的均值.

因为该方法存在缺点，导致工业性并未采用：
1）要求物体必须是封闭的（即水密的，watertight）；
2）开销可能并不值得. 因为所有片元深度必须比较2次，才能得到最小和次小深度.

锯齿（Aliasing）

Shadow Maps对场景，是一种离散表示，有一定分辨率. 如果分辨率不够大，就可能存在锯齿（Aliasing）的现象.

如下图阴影：

实时渲染中的数学

近似相等

RTR中，我们不关心不等式，关心近似相等（approximately equal）.

RTR中一个重要近似相等：

\[\int_Ωf(x)g(x)dx≈\frac{\int_Ωf(x)dx}{\int_Ωdx}\cdot \int_Ωg(x)dx \]

什么时候结果是准确的（可接受）？

有2种情况，

1）实际积分范围小的时候（Small support）；
2）g(x)足够光滑（Smooth integrand），即在积分范围内变化不大.

实时渲染方程的近似相等

RTR中的渲染方程（带可见性）：

\[L_o(p,ω_o)=\int_{Ω^+}[L_i(p,ω_i)][f_r(p,ω_i, ω_o)cosθ_i][V(p,ω_i)]dω_i \]

近似求解：

\[L_o(p,ω_o)≈\frac{\int_{Ω^+}V(p,ω_i)dω_i}{\int_{Ω^+}dω_i}\cdot \int_{Ω^+}L_i(p,ω_i)f_r(p,ω_i, ω_o)cosθ_idω_i \]

注：这个公式会在后面用到.

什么时候积分准确?

1）积分范围足够小的时候（点光源 / 方向光源）；
2）被积函数光滑（漫反射BSDF / 恒定radiance的面光源）.

对于1），光源是点光源或方向光源时，在前面路径追踪（参见计算机图形：Path Tracing）中讲过，为了避免大量光线浪费，我们对光源进行积分. 如果光源面积足够小，那么积分范围足够小.

对于2），
面光源辐射的radiance恒定，可认为\(L_i(p,ω_i)\)不变.

当表面是diffuse材质，发生漫反射，BSDF可认为是光滑的；
当表面是glossy材质，BSDF不能认为是光滑的.

关于材质，参见计算机图形：材质和外观

BSDF = BRDF + BTDF

S: Scattering，散射；
R: Reflective，反射；
T: Transmit，折射.

软阴影

基本概念

如果使用了面光源或者体积光源，那么则会产生软阴影.

硬阴影（Hard Shadows）：没有从有阴影到无阴影的界限.
软阴影（Soft Shadows）：从有阴影到无阴影，有一个过渡. 看起来会更自然.

在日食的光照模型中，如果从光源看向阴影，会有部分被遮挡，部分没被遮挡，这就是软阴影的本质.

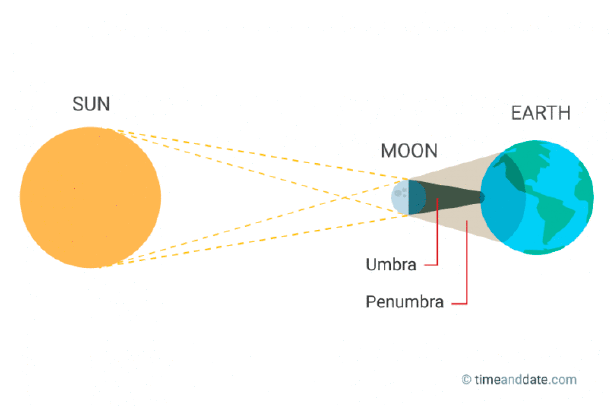
from: https://www.timeanddate.com/eclipse/umbra-shadow.html

本影(umbra)：完全被覆盖的阴影区域，如日食时完全被遮挡的部分；
半影(penumbra)：部分被阴影覆盖的区域，如日食时部分被遮挡的过渡带.

shadow = umbra + penumbra

PCF

百分比渐进过滤(Percentage Closer Filtering, PCF) 可用来做阴影边缘的抗锯齿的功能. 如果用PCF来做软阴影，则称为百分比渐进软阴影（Percentage closer soft shadows, PCSS）.

PCF不是对最后具体的阴影进行filter，也不是对最后的shadow map进行filter.

在之前的阴影贴图中，对片元P点着色时，如何判断P是否在阴影里？

投影到Light视角后，连接P与光源（Light），得到其深度（光源视角），然后与shadow maps上该方向的深度进行比较，看是否是距离光源最近的点. 这里做了一次比较.
tips: shadow maps上每个像素值代表一个深度.

PCF与阴影贴图的区别：投影到Light视角后，我们在shadow maps上找一圈（如7x7）的像素（深度），每一个深度都与片元深度进行比较；然后，将比较结果（0或1）求平均.

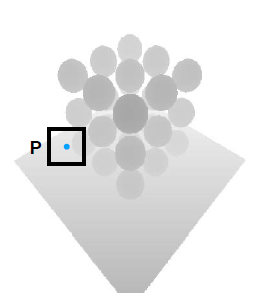
例如，对于地面上P点，投影到光源视角后，

1）将其深度与方框内所有像素（如3x3区域）的深度进行比较

2）获取比较结果，例如

1,0,1,
1,0,1,
1,1,0

挡住是0，未挡住是1.

3）求平均值，得到visibility（可见性），如0.667
当然，也可以进行加权平均.

求visibility：

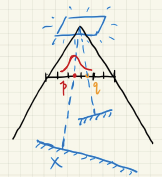
上图中，x是shading point，x投影到shadow map上像素点为p，p像素值代表挡住x的点的深度（如果p depth < x depth）.

PCF考虑的不仅仅是p，而是p周围一圈的像素（大小filter size），会对该区域的每个像素点的深度都与x深度进行比较，从而判断有哪些点挡住了x.
最后，将比较结果加权平均，于是得到visibility.

如果用数学表达这个过程，那就是滤波器（Filter）/卷积（convolution）：

\[[\omega * f](p)=\sum_{q\in N(p)}\omega(p,q)f(q) \]

其中，

• \(N(p)\)代表p点邻域
• \(f(q)\)是q depth与x depth比较结果（是否挡住x）
• \(\omega(p,q)\)是求平均时权值

在PCSS中，我们最终要得到是的x点的Visibilty，即

\[V(x)=\sum_{q\in N(p)}\omega(p,q)\cdot χ^+[D_{SM}(q)-D_{scene}(x)] \]

其中，

• \(χ^+\)是符号函数，值域{0,1}. 0代表q挡住x，1代表q未挡住x
• \(D_{SM}\) shadow map上q点的depth
• \(D_{scene}\) x点的depth

当\(D_{SM} - D_{scene} < 0\)时，\(χ^+[D_{SM}(q)-D_{scene}(x)]=0\)，代表q距离光源更近，即q挡住x；

否则，\(χ^+[D_{SM}(q)-D_{scene}(x)]=1\)，代表q未挡住x.

注意：

1）PCF并不直接对shadow map进行过滤（filter）/模糊，因为shadow map存放的是Light视角的depth，而我们要求的\(V(x)\)是x的可见性

\[V(x)\neq χ^+\{[\omega * D_{SM}](q)-D_{scene}(x)\} \]

2）PCF也不是在图像上做过滤（filter）

\[V(x)\neq \sum_{y\in N(x)}\omega(x,y)V(y) \]

PCF效果图

下图是直接对阴影的结果（图像）进行filter，得到的不是软阴影：

可以看到，仍然有锯齿问题.

下图是用PCF的处理效果：

可以看到，没有锯齿问题，有较好的软阴影效果.

PCF过滤窗口大小（filtering size）与软阴影：
1）越小，得到的阴影越锐利；
2）越大，得到的阴影越柔和；

PCSS

能否用PCF实现软阴影效果？

答案: 是的. 可以用一个比较大的filtering size. 但不是越大越好，阴影不是越软越好.

例如，下图中，有些地方阴影应该硬，有些地方应该软：

不难发现，距离钢笔尖（光线的遮挡物）越近的地方，阴影越锐利；距离越远，阴影越柔和.

于是，针对不同地方，应该有不同的filter size，以得到不同的阴影的柔和效果.

• Filter size <-> 遮挡物距离（blocker distance），准确来说，相对平均的、投射的遮挡物的深度(relative average projected blocker depth)

确定filter size

如何确定filter size？

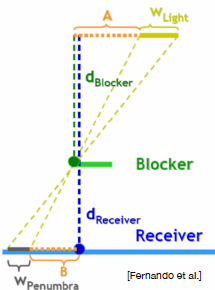
如上图，根据三角形相似性：

\[\frac{w_{Penumbra}}{d_{Receiver} - d_{Blocker}}=\frac{w_{Light}}{d_{Blocker}}\\ w_{Penumbra}=(d_{Receiver} - d_{Blocker})\cdot \frac{w_{Light}}{d_{Blocker}} \]

其中，

• \(w_{Penumbra}\) 半影区域宽度(Penumbra width)，即软阴影区域宽度，通常用该项作为filter size；/
• \(w_{Light}\) 光源区域的宽度(Light width)；
• \(d_{Receiver}\) 光源到Receiver的距离(Receiver depth)；
• \(d_{Blocker}\) 光源到遮挡物的距离(Blocker depth).

注意: 光源是面光源（或称区域光，Area Light）. PCSS的核心目标是模拟软阴影（边缘柔和的阴影），而软阴影通常由非点光源（如面光源、线光源等）产生.

blocker不一定是一个规则的平面，可能是球心，钢笔形状，或其他任意形状. 对于一个shading point，我们要计算的是，在一定范围内，在shadow map上有多少挡住它的像素，这些像素记录的深度的平均值，就是blocker depth.

为了确定filter size，我们得确定blocker到shading point的距离，即\(d_{Receiver} - d_{Blocker}\)

PCSS算法步骤

1）Blocker search：搜索Blocker，在一定区域内得到blocker depth平均值

shading point连向点光源，找shadow map上周围的一个区域，判断shading point是否在阴影里.
如果在阴影里，那么找到的那个像素对应的深度，就是blocker depth. 当然，我们会找附近几个像素点对应的区域的深度值，求平均，作为blocker depth平均值.

2）Penumbra estimation：半影估计，计算\(w_{Penumbra}\)

用平均blocker depth计算出\(w_{Penumbra}\)，从而决定filter size.

3）PCF filter

确定了filter size，就能进行PCF过滤.

搜索blocker时，应该用多大范围？

2类方法：
1）用一个常数区域，如5x5；
2）启发式方法可能更佳.

启发式方法：连接面光源与shading point，形成四棱锥，与shadow map（假设放在Light视角观察空间的近平面）相交的区域，就是可能遮挡shading point的区域.

第1）、3）步会访问邻域范围所有像素，然后再求平均，可能会很慢. 如何解决这个问题？

答：在对应区域内随机取样. 不过可能会存在噪声，可以在图像空间降噪处理.

VSSM

方差软阴影映射（Variance Soft Shadow Mapping，VSSM）

• 针对性解决PCSS中，第1）步（blocker search）、第3）步（PCF filtering）慢的问题.

• PCF中，如何知道：

  • 在shading point前面的texels的百分比，即有多少texels深度 < shading point depth？
  • 有多少texels在搜索区域范围内？

如果知道这两点信息，是不是就能知道，在搜索区域内，有多少texels遮挡了shading point？

这就好比一场考试中，我知道自己成绩，如何知道自己排名第几，有多少人比自己考得好.

可以用直方图来精确回答该问题，但直方图的前提是对所有数据统计；可以用正态分布（Normal distribution）近似回答该问题.

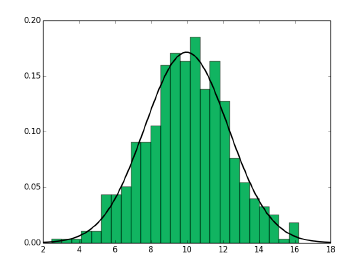
而用正态分布的关键点是：快速计算区域内深度的期望（mean）和方差（variance）.

• 求期望（均值）

1）求平均值可以用硬件MIMAP（Hardware MIPMAPing），缺点只能求正方形区域均值；

2）Summed Area Tables (SAT)，也称为积分图（Integral Image），一种用于快速计算矩形区域求和的数据结构和算法.

• 方差

\[Var(X)=E(X^2)-E^2(X) \]

可以用另一张texture存放\(depth^2\)，从而计算其期望；
实践中，shadow map像素值R通道可存放深度（depth），B通道可存放深度平方（\(depth^2\)）.

回到我们的主体. 我们求期望、方差，是为了求出正态分布的pdf，进而求出有多少texels深度比x深度大，有多少texsel深度比x深度小. 这就是概率论中的CDF（Cumulative Distribution Function，累积分布函数）.

CDF定义：对于一个随机变量 X，其累积分布函数\(F_X(x)\)定义为：

\[F_X(x) = P(X\le x) \]

即\(F_X(x)\)表示随机变量X取值小于等于x的概率.
​

CDF(x)的几何意义：PDF(x)对x在\((-∞,x]\)上求积分结果（下图阴影面积）.

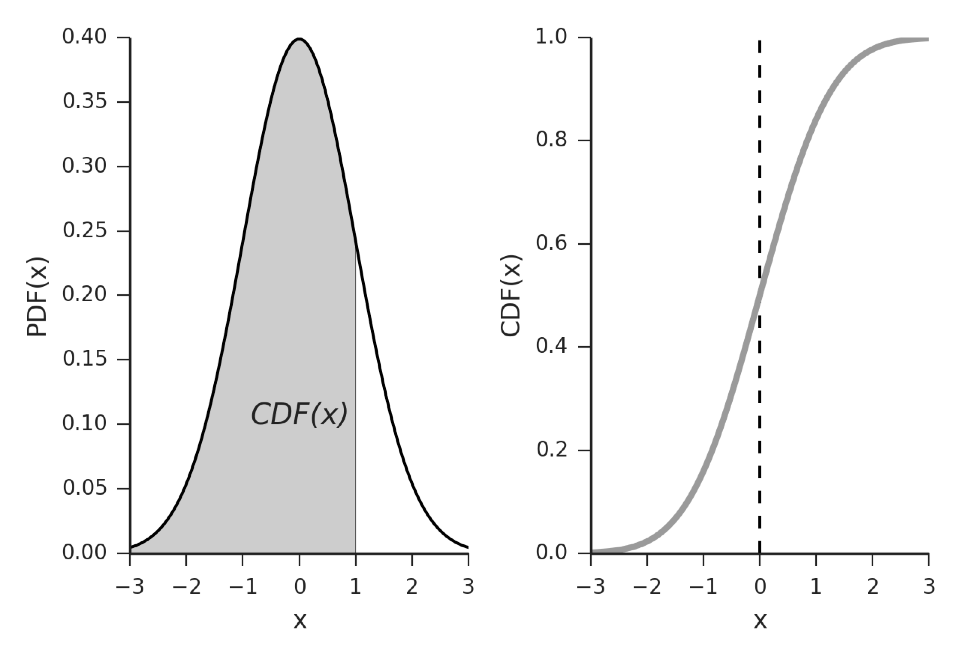
该积分解没有解析函数，不过有数值解，称为Error Function（误差函数）. C++中erf实现了该功能.

VSSM用一个不等式对其进行了改进：

• 单边切比雪夫不等式（On-tailed Chebyshev's Inequality）

描述任意随机变量的取值偏离其期望值的概率上限.

单边切比雪夫不等式定义：

设 X 是一个随机变量，其期望为 \(μ\)，方差为 \(σ^2\). 则对任意正数 t > 0，有：

\[P(X-μ\ge t)\le \frac{σ^2}{σ^2+t^2} \]

证明参见：概率论：切比雪夫不等式

可用单边切比雪夫不等式求得概率\(P(X>t)\)，即下图阴影面积：

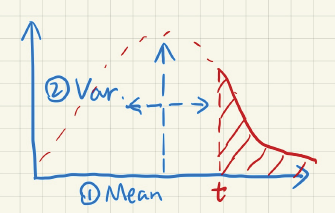
切比雪夫不等式不要求正态分布.

针对PCSS第3）步，根据切比雪夫不等式，知道shadow map上有多少（百分比）像素深度比shading point大，有多少比shadping point小，再乘以filter size，就能得到数量. 进而求出visibility.

针对PCSS第1）步，我们要求的是在一个区域范围内，遮挡住shadping point的blocker的平均深度. 而整个区域的平均深度可以通过Hardware MIPMAPS或者SAT快速求解，记为\(z_{avg}\).

我们关心的是shadow map上指定区域内，深度 < shading point 的点.

假设blocker(z<t)的平均深度\(z_{occ}\)，non-blocker(z>t)的平均深度\(z_{unocc}\).

设non-blocker的像素数量\(N_1\)，blocker的像素数量\(N_2\)，像素总数\(N=N_1+N_2\)

有，

\[\frac{N_1}{N}z_{unocc}+\frac{N_2}{N}z_{occ}=z_{avg} \]

记shading point深度为t，
\(\frac{N_1}{N}=P(X>t)\)，可通过切比雪夫不等式求解\(P(X>t)\)；

\(\frac{N_2}{N}=P(X<t)=1-P(X>t)\).

我们要求的是\(z_{occ}\)，现在还差\(z_{unocc}\)未知. 由于shadow receiver（阴影接收者）常常是一个平面，因此假设非遮挡物深度与shading point深度一样，即\(z_{unocc}=t\)

下图是VSSM阴影效果：

from: https://developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch08.html

MIPMAP

给定一个区域，如何快速得出该区域平均值？并且该区域保证是矩形.

之前提过有两种方法：

1）MIPMAP

2）SAT

MIPMAP做的是快速的、近似的、方形的范围查询.

对于一张纹理贴图，我们每次减小其一半分辨率，得到一组Mimmap.

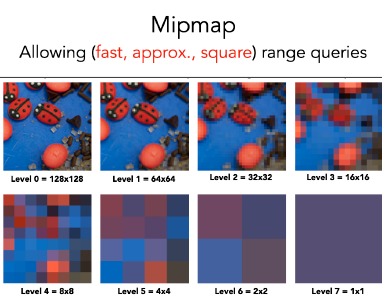
如果原图(Level 0)的任意位置(x,y)，如何在Level 5上找到对应位置？
那就需要做双线性插值.
具体可参见GAMES101 Lecture 09

缺点：

1）因为是做插值，所以不准；
2）如果如果查询范围不与现成Mipmap的level一致，就需要在Mipmap的层级之间插值，即三线性插值.

SAT

SAT(Summed Area Tables), 是一种求和的经典数据结构和算法，与前缀和算法紧密联系.

• 1维

数据结构如下：

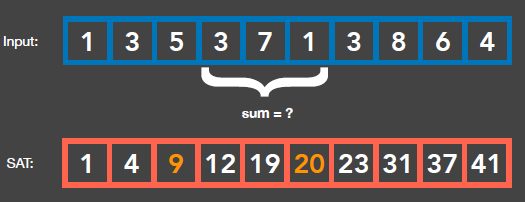
SAT的每个元素，代表的是从输入第0个元素开始，加到这个位置元素的和. 即\(SAT[i]=sum\{input[0],...,input[i-1]\},i=0,1,...,n\)

这样，当我们想求input的第3~5个元素和时，
\(SAT[5]-SAT[2]=20-9=11\)

• 2维

如下图，对于2维情况，我们如何求蓝色矩形内所有值的内？

从左到右依次是：蓝色矩形、绿色矩形、左半边橙色矩形、右半边橙色矩形、左上角绿色矩形

绿色矩形 - 左半边橙色矩形 - 上半边橙色矩形 + 左上角绿色小矩形 = 蓝色矩形

式中，除了蓝色矩形，其他矩形的起点都是左上角. 于是，可以预计算一张表，表里的元素表示，从左上角开始加到当前位置元素（图中白色点）的和，对应整个矩形的值.

i.e. 我们只需要查4次，就能得到指定矩形区域内所有元素的和.

如何建立该SAT？

每行都是一个1维SAT，代表这一行从左加到右对应的和；每一列都是一个1维SAT，代表这一列从上到下对应的和. i.e. 只需要横着对每行做一遍，竖着对每一列做一遍.

由于横、竖计算和相互独立，因此可以用GPU加速.

Moment Shadow Mapping

VSSM存在缺陷：
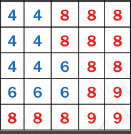
对于一些特殊的障碍物，如下图右，如果还是按正态分布来估计深度，那么得到的阴影是不正确的.

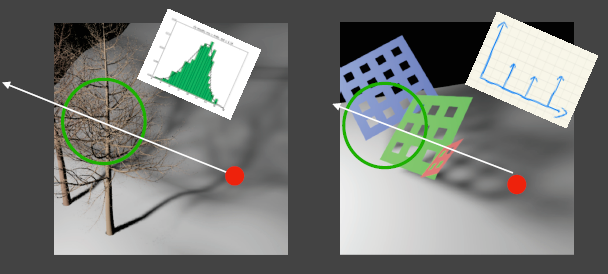
深度分布不准确，可能导致2类问题：
1）过暗：可能可以接受
2）过亮：漏光（Light Leaking）

问题原因：真实的障碍物深度(x)对应概率密度函数(f(x))，可能如下图蓝色曲线，而我们用红色的正态分布曲线来计算，会导致\(P(X>t)\)多算了（对应图中阴影面积），也就是障碍物少算了，最终导致漏光现象.

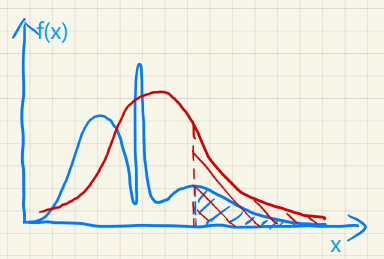
于是，Peters提出Moment Shadow Mapping（MSM） 解决该问题. Moment Shadow Mapping是一种改进的阴影映射技术，用于生成更高质量的软阴影（Soft Shadows）. 它通过高阶矩（Moments）来存储深度分布信息，相比传统的Shadow Mapping或Variance Shadow Mapping（VSM），能更有效地减少阴影的走样（Aliasing）、光渗（Light Bleeding）（俗称漏光）等问题.

PCSS中，shadow map存放depth的一阶信息，用于表示Light视角的深度信息；
VSMM中，存放depth的一阶、二阶信息，其中二阶用于快速求方差；
Moment Shadow Mapping中，通过高阶矩（Moments），存放depth更高阶的信息.

如下图，分别是PCF和一系列阶跃函数堆积而成的函数（深度的CDF），每条曲线最高价分别是2、3、4.

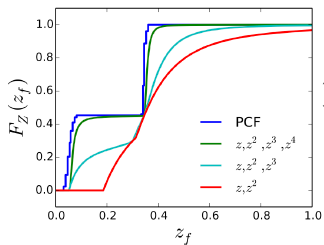
PCF是对filter size区域的depth与shading point比较结果求平均，因此较为准确；
阶跃函数堆积而成的函数是对深度的估计，因此可能存在较大误差.

m阶的moments，能存放m/2阶梯. 上图最高4阶阶跃函数，因此最多存在2个台阶.

通常，使用4阶moments即可，能实现较好阴影效果.

下图是使用VSSM和Moment Shadow Mapping的效果对比：

可以看出，Moment Shadow Mapping效果更好，不存在漏光现象.

Distance Field Soft Shadows

距离场软阴影（Distance Field Soft Shadows，DFSS），一种基于有向距离场（Signed Distance Field, SDF）的高效软阴影渲染技术.

核心思想：通过距离场快速估算光线与遮挡物的接近程度，动态计算阴影的软硬程度.

先来看一个使用DFS和Hard Shadow渲染阴影效果对比：

使用DFS的阴影明显柔和很多.

距离函数（Distance Functions）：

在空间中任意一点，定义它到某个物体表面上最近一个点的距离，即它到物体表面的最小距离. 这个距离是有向距离，带正负号，例如，物体内部为负号，物体外部为正号.

距离场（[Signed] Distance Field），通常缩写为SDF.

下图是字母A的SDF：

左图，图上任一点都能计算该点到字母A的轮廓的最近距离，距离A越远，值越来越小，看起来越来越模糊；
右图，类似等值线，类比于地图的等高线，同样颜色表示的值一样，因此轮廓看起来是一圈圈的.

上图blend（混合）运动的边界. A、B两张图，左半边（黑色）有个物体，在从左往右移动.

假设A代表某个时刻，物体在黑白边界；B代表未来另一个时刻，物体移动到新的黑白边界.

现在对A、B进行线性插值：取A、B相同位置像素，做线性平均（如A占50%、B 占50%），可得到第三幅图（lerp(A,B)）.

但是，这样得到的是中间灰色过渡带. 如何能得到在中间的边界？

现在我们做些改进.
我们定义，在物体内部（黑色部分），规定为负值，物体外部（白色部分），规定为正值. 随着点距离边界不同位置，可以赋以不同大小.

于是，可以得到如下图所示A、B转化而成的SDF. 这样，我们对A、B对应位置的SDF做线性平均，可得到第三幅图（lerp(SDF(A),SDF(B))）.

然后，根据SDF=0，可恢复出边界.

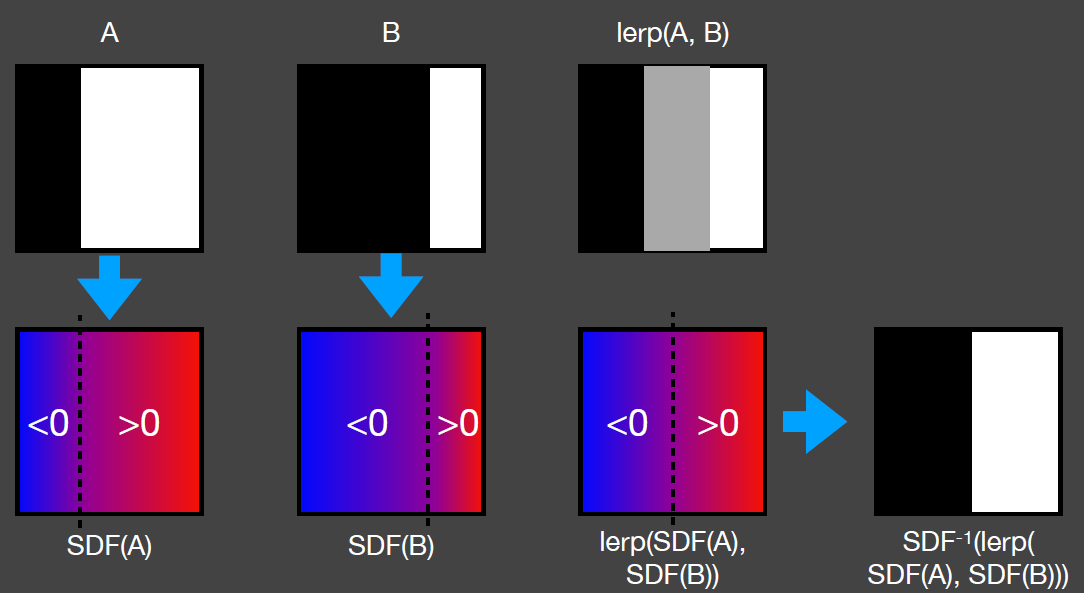
优点：可表示物体边界，不需要关注物体拓扑关系.

如何计算场景的SDF？

可以每个问题单独计算SDF，然后空间中每个点的SDF是所有物体SDF的最小值.

SDF的使用

• 应用1

光线步进（Ray Marching）（球体追踪）：假设已经得到场景的SDF，现在有一根光线，就能对光线和SDF所隐含的表面求交

SDF背后隐含了一个思想：
SDF的数值等于一个“安全”半径范围，在安全范围内，不可能与任何物体相交.

于是，任何时候在p点，都能往给定方向往前轴SDF(p)的距离，不会与其他物体相交.

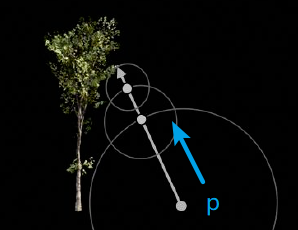
优缺点：
场景中每个点都需要计算并存储SDF，所需存储量极大；

运动的物体，可以用SDF，但形变的物体不行，因为物体的SDF需要重新算一遍.

• 应用2

使用SDF（有向距离场）估算遮挡百分比（percentage of occlusion）.

任意一个点的SDF，告诉我们一个安全角度（从眼睛看向物体）

越小的安全角度，意味着更少的可见性.

如下图，在光线步进过程中，从眼角出发，在每一步计算安全角度. 我们取最小的安全角度，就能知道阴影偏黑，还是偏白.

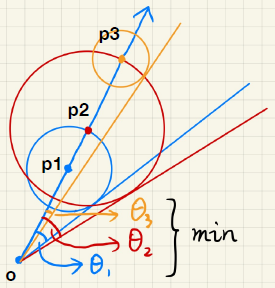
计算p点安全角度：

\[sin\theta = \frac{SDF(p)}{p-o}\\ \theta = arcsin \frac{SDF(p)}{p-o} \]

但是，在shader和RTR中，反三角计算量非常大，通常应该避免. 可以用下面方法减少计算量：

\[\theta = min\{\frac{k\cdot SDF(p)}{p-o},1.0\} \]

k作用：
一个比较大的k值，意味着很小的安全角度也会被当做1，0~1之间过渡带变窄. 极端情况下，k特别大，会变成硬阴影，要么是0，要么是1.

• 距离场做软阴影

优势（Pros）：
1）快（忽略了距离场的生成时间）
2）高质量

缺点（Cons）：
1）需要预计算（precomputation）
2）需要大量存储（三维场景中每个点都需要存储SDF）

小结

点光源本来就应该产生Hard Shadow，所以不用考虑PCSS；面光源、多个光源，才会产生Soft Shadow，需要考虑PCSS.

参考

[1] Games202 Lecture3

[2] Tomas Möller, Haines E .Real-Time Rendering 4th Edition[M].DBLP,1999.

[3] Peters C , Klein R .Moment shadow mapping[J].ACM, 2015.DOI:10.1145/2699276.2699277.