概率论：切比雪夫不等式

目录

• 切比雪夫不等式
  • 双边切比雪夫不等式
  • 单边切比雪夫不等式
• 参考

切比雪夫不等式

双边切比雪夫不等式

双边切比雪夫不等式，即经典切比雪夫不等式，描述了任意随机变量的取值偏离其期望值的概率上限，不依赖于具体分布，仅需要方差存在.

定理 设随机变量X的期望\(E(X)=μ\)，方差\(D(X)=\sigma^2\)，则对于任意整数\(ε\)，不等式

\[P\{|X-μ|\ge ε\}\le \frac{\sigma^2}{ε^2} \]

成立. 该不等式称为切比雪夫不等式(Chebychev’s inequality).

证明：
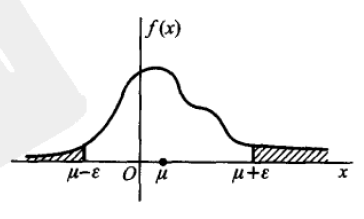
设连续型随机变量X，概率密度\(f(x)\)

∵\(|X-μ|\ge ε > 0\)
∴\(\frac{|X-μ|}{ε}\ge 1\)
∴\(\frac{|X-μ|^2}{ε^2}\ge 1\)

有

\[\begin{aligned} P(|X-μ|\ge ε)&=\int_{|X-μ|\ge ε}f(x)dx\le \int_{|X-μ|\ge ε}\frac{|X-μ|^2}{ε^2}f(x)dx\\ &=\frac{1}{ε^2}\int_{|X-μ|\ge ε}|X-μ|^2f(x)dx=\frac{\sigma^2}{ε^2} \end{aligned} \]

切比雪夫不等式的几何意义，是\(f(x)\)与x轴围成的区域在\(x\in (-∞, μ-ε]\)以及\(x\in [μ+ε,+∞)\)上的面积.

上面不等式描述的是两端面积，还能写成等价形式，描述中间面积：

\[\begin{aligned} P(|X-μ|<ε) &= 1-P\{|X-μ|\ge ε\}\\ & \ge 1-\frac{\sigma^2}{ε^2} \end{aligned} \]

单边切比雪夫不等式

要证明单边切比雪夫不等式，需要先引入马尔可夫不等式. 马尔可夫不等式用于估计非负随机变量超过某阈值的概率上界。

定理 令X为一非负随机变量，假设\(E(X)\)存在，对任意\(t>0\)，有

\[P(X>t)\le \frac{E(X)}{t}. \]

该不等式称为马尔可夫不等式（Markov's inequality）

证明：
∵\(X>0\)
∴

\[\begin{aligned} E(X) &= \int_{0}^∞xf(x)dx=\int_{0}^txf(x)dx+\int_{t}^∞xf(x)dx\\ &\ge \int_{t}^∞xf(x)dx \ge t\int_{t}^∞f(x)dx=tP(X>t) \end{aligned} \]

又\(t>0\)
∴\(P(X>t)\le \frac{E(X)}{t}\)

单边切比雪夫不等式是经典切比雪夫不等式的单侧形式，用于估计随机变量偏离其期望值超过特定阈值的概率上届.

定理 设随机变量的期望\(E(X)=μ\)，方差\(D(X)=\sigma^2\)，对于任意\(t>0\)，有

\[P(X-u\ge t)\le \frac{\sigma^2}{\sigma^2+t^2} \]

该不等式称为单边切比雪夫不等式（One-tailed Chebychev’s inequality）.

证明：设\(Y=X-μ\)

有\(E(Y)=E(X-μ)=E(X)-μ=0\)，

\(E(Y^2)=E[(X-μ)^2]=E(X^2-2μX+μ^2)=E(X^2)-2μE(X)+μ^2=E(X^2)-μ^2=D(X)=\sigma^2\)

∴\(D(Y)=E(Y^2)-E^2(Y)=\sigma^2\)

应用马尔可夫不等式，对于任意\(a>0\)，

\[P(Y\ge t)=P(Y+a\ge t+a)\le P((Y+a)^2\ge (t+a)^2)) \le \frac{E[(Y+a)^2]}{(t+a)^2} \]

注意马尔可夫不等式应用条件：\(P(X\ge t)\le \frac{E(X)}{t}\)，要求\(X\ge 0\)
而我们不确定\(Y,Y+a\)符号，所以得到平方形式\((Y+a)^2\).

\[E[(Y+a)^2]=E(Y^2+2aY+a^2)=E(Y^2)+2aE(Y)+E(a^2)=\sigma^2+a^2 \]

∴

\[P(Y\ge t)\le \frac{\sigma^2+a^2}{(t+a)^2} \]

考察\(f(a)=\frac{\sigma^2+a^2}{(t+a)^2}\)，什么时候能取得最小值，以得到\(P(Y\le t)\)的最小上界？

\[f'(a)=\frac{2a(t+a)^2-(\sigma^2+a^2)2(t+a)}{(t+a)^4} \]

∵\(f(a)\)在\(a>0\)上是连续函数
∴考察其导数

令\(f'(a)=0\)，即

\[2a(t+a)^2-(\sigma^2+a^2)2(t+a)=0\\ a(t+a)-(\sigma^2+a^2)=0\\ a=\frac{\sigma^2}{t} \]

对于\(a > 0\)，

\[f'(a)=2\frac{at-\sigma^2}{(t+a)^3} \]

当\(a<\frac{\sigma^2}{t}\)时，\(f'(a)<0\)
当\(a>\frac{\sigma^2}{t}\)时，\(f'(a)>0\)

∴\(f(a)\)在\(a=\frac{\sigma^2}{t}\)处取得最小值，即

\[f(\frac{\sigma^2}{t})=\frac{\sigma^2+a^2}{(t+a)^2}=\frac{\sigma^2+(\frac{\sigma^2}{t})^2}{(t+\frac{\sigma^2}{t})^2}=\frac{t^2\sigma^2+\sigma^4}{(t^2+\sigma^2)^2}=\frac{\sigma^2}{t^2+\sigma^2} \]

∴

\[P(X-μ\ge t)=P(Y\ge t)\le {f(a)}_{min}=f(\frac{\sigma^2}{t})=\frac{\sigma^2}{t^2+\sigma^2} \]

参考

[1]盛骤,谢式千,潘承毅.概率论与数理统计 第四版[M].高等教育出版社,2008.
[2]L.沃塞曼.统计学完全教程[M].科学出版社,2008.