计算机图形：Path Tracing（路径追踪）

Whitted-Style Ray Tracing
路径追踪
小结
参考

Whitted-Style Ray Tracing

之前介绍的光线追踪方法（参见计算机图形：全局光照），是Whitted-Style Ray Tracing.

核心思想：

从视点向成像平面上每个像素发射光线，求出与该光线相交的最近物体的交点. 如果该点表面是漫反射表面，则计算光源直接照射到该点产生的颜色；如果是镜面或折射表面，则继续反射或折射方向跟踪另一条光线，如此递归下去，直到光线逃出场景或者达到最大递归深度.

特点：

总是进行镜面反射（specular reflections）/折射（refractions）计算；
遇到漫反射表面终止光线弹射.

缺点：

问题1

Whitted-Style Ray Tracing遇到漫反射表面终止光线弹射，所以对于漫反射材质物体的渲染不真实（glossy reflection），光线不应该停下来，而且忽略了漫反射物体发射

问题2

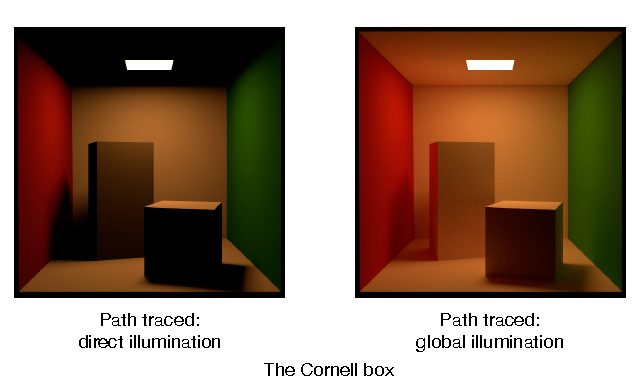
环境缺少漫反射产生的效果，如左图中，没有红墙反射的光线的效果.

路径追踪

Whitted-Style Ray Tracing 存在渲染不真实的问题，但渲染方程是正确的.

渲染方程：

\[L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{Ω^+}L_i(p,\omega_i)f(p,\omega_i,\omega_o)(n\cdot \omega_i) d\omega_i \]

tips：

1）上式右边积分是在半球面上的积分，于是可用蒙特卡洛积分法求解. （参见计算机图形：辐射度光照模型）；
2）右边积分是在不同方向上的积分，在不同方向上采样，随机选一些方向作为随机变量.

简单蒙特卡洛解决方案

只考虑光线的一次弹射.

假设所有点不发光，借用反射方程作为渲染方程：

\[L_o(p,\omega_o)=\int_{Ω^+}L_i(p,\omega_i)f(p,\omega_i,\omega_o)(n\cdot \omega_i) d\omega_i \]

用蒙特卡洛积分求解该渲染方程.

蒙特卡洛积分：

\[\int_a^b f(x)dx \approx \frac{1}{N}\sum_{k=1}^N\frac{f(X_k)}{p(X_k)}, X_k\sim p(k) \]

积分中，

\(f(x)\)：\(L_i(p,\omega_i)f(p,\omega_i,\omega_o)(n\cdot \omega_i)\)
PDF：用最简单的均匀采样，\(p(\omega_i)=1/2\pi\)

∴可将渲染方程写成蒙特卡洛积分方式：

\[\begin{aligned} L_o(p, \omega_o) &= \int_{Ω^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot \omega_i)d\omega_i\\ &\approx \frac{1}{N}\sum_{i=1}^N\frac{L_i(p,\omega_i)f(p,\omega_i,\omega_o)(n\cdot \omega_i)}{p(\omega_i)} \end{aligned} \]

至此，我们可以对任何一个着色点的出射radiance进行计算. 对于直接光照，对p点着色伪代码：

// 从p点入射的光线随机选N方向
// 如果这些光线打到了光源, 就用蒙特卡洛积分所得结果加到出射radiance Lo中.
// 打到光源, 自然知道L_i; 入射方向、出射方向都知道, f_r (brdf)自然知道;
// 方向知道, cosine也就知道; pdf 是均匀采样一个点, 值也知道
shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1/N) * L_i * f_r * cosine / pdf(wi)
    Return Lo

注：对于着色点，均匀采样的\(pdf(w_i)\)是\(p(\omega_i)=1/2\pi\).

全局光照

前面选取的光线，如果打到的不是光源，而是物体，怎么办？

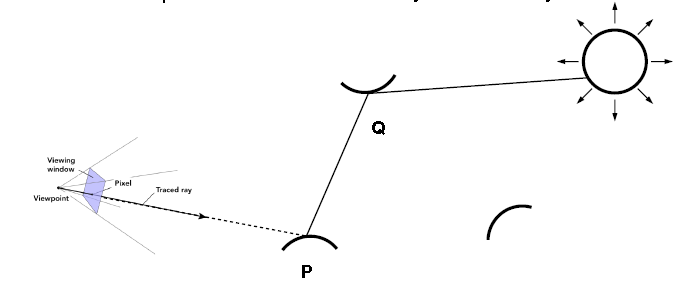
例如，下图P发出的一条光线打到另一点Q（Q不是光源）. 此时，需要考虑Q点出射radiance对P点影响.

shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

这种方式存在一个问题：需要计算的光线数量\(\#rays\)，随着弹射次数\(\#bounces\)增加，爆炸式增长.

\[\#rays = N^{\#bounces} \]

注：N是常数.

例如，N=100

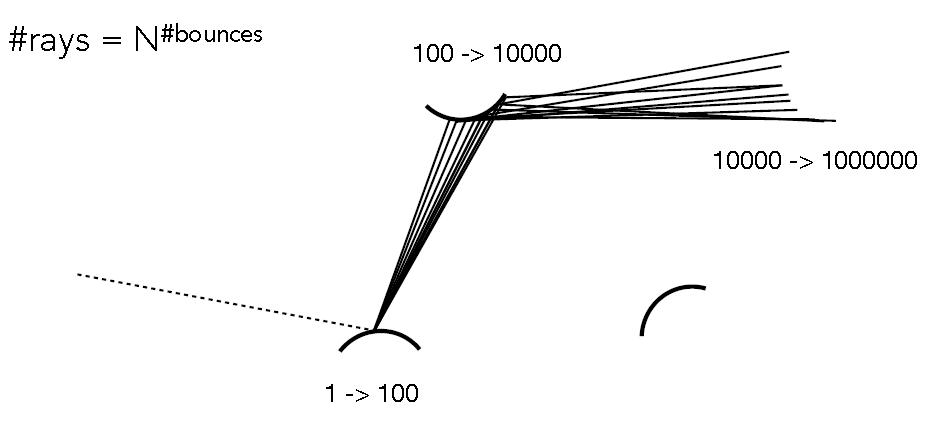
有没有N值，可以让\(\#rays\)不爆炸式增长？
可取N=1. 在每次着色点时，只追踪1条光线.

shade(p, wo)
    Randomly choose 1 direction wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

这就是路径追踪（path tracing）（N≠1时，是分布式光线追踪）.

光线生成

如果着色点的过程中，只追踪一条光线，那么势必会产生噪声. 如何解决噪声？

只需要对每个像素追踪更多光线路径，并取其radiance的平均值即可.

最终目的是将结果渲染到屏幕像素，因此，可以从一个像素发射多条光线，将着色的结果求平均.

// 像素内部均匀取N个样本位置
// 对每个选取位置, 连一个从相机到样本的线
ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p
            pixel_radiance += 1 / N * shade(p, sample_to_cam)
    Return pixel_radiance

俄罗斯轮盘赌

还存在一个问题：shade(p,wo)代码中存在递归，递归何时终止？即光线是否要无限追踪下去？什么时候停止？

实现固定反弹次数，都不太合适，因为有的区域会损失能量，造成渲染偏暗.

解决办法：用俄罗斯轮盘赌（Russian Roulette, RR）的思想.

俄罗斯轮盘赌有两种结果：

1）概率P，0 < P < 1，存活；
2）概率1-P，死亡.

假设枪里有2颗子弹，那么存活概率：\(P=4/6\)

此前，我们从着色点发射一条光线，并且获取着色结果Lo（outgoing radiance）.

假设我们手动设置概率P(0 < P < 1)，

对于概率P，发射光线并且将着色结果除以P：Lo/P
对于概率1-P，不用发射光线P并且将得到结果0

最终的期望仍然是Lo：

\[E=P*(Lo/P)+(1-P)*0=Lo \]

对应代码：

// 手动设置一个概率P_RR, 0 < P_RR < 1
// 然后从均匀分布[0,1]中随机选一个数 ksi
// 如果 ksi > P_RR, 无需生成光线
shade(p, wo)
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1]
    If (ksi > P_RR) return 0.0;

    Randomly choose 1 direction wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) / P_RR
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
    Return Lo

光源采样

到目前为止的路径追踪方法，方法是正确的，但依然存在问题：对于低采样率（Low SPP），噪声比较大.

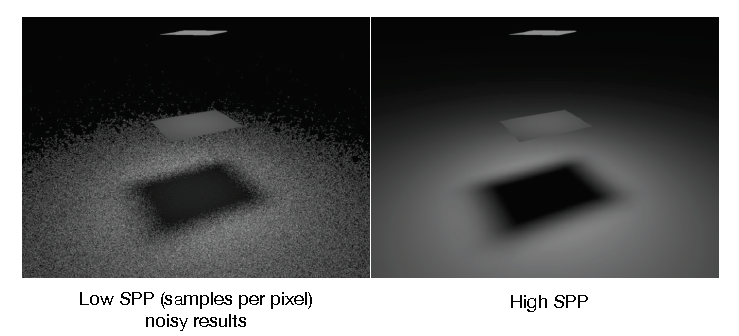
这是因为从物体表面一点发射的光线是均匀采样的，而不同的面光源，不同的光线采样数量，才能有1条光线与光源相交：

1）如果光源偏大，可能平均需要5条光线；
2）如果光源适中，可能需要500条光线；
3）如果光源偏小，可能需要50000条光线.

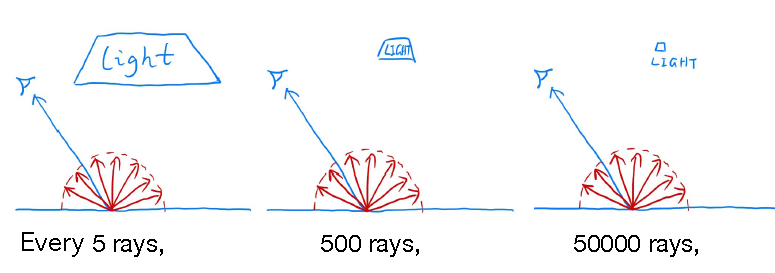
由于是均匀采样，会往四面八方发射光线，会有大量光线浪费了，不可能打到光源.

如何解决这个问题，避免大量光线浪费？

我们之前采样的光线是在物体表面，如果是在光源表面采样，连接采样点与物体表面点，这样就不存在浪费问题.

如下图，对于着色点\(x\)，不再均匀地往四面八方采样发射光线，而是在光源上采样. 光源本身朝向\(\bm{n'}\)，面元\(dA\)，对应位置\(x'\)，与着色点连线得到 \(xx'\) ，会与各自法向量产生2个角：
1）\(θ\) 连线与着色点的法向量夹角；
2）\(θ'\) 连线与光源的法向量夹角.

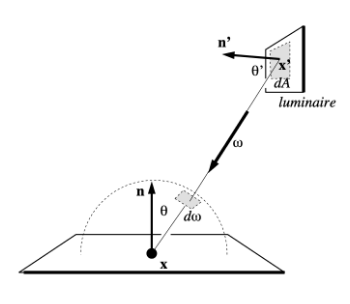
假定光源是一个矩形的框，面积大小A，我们在光源上均匀采样. 那么，

\[pdf=1/A(∵\int pdf\space dA = 1) \]

但是，渲染方程中的积分是定义在物体表面的，而不是光源：

\[Lo=\int Li\space fr\space cos\space \bm{d\omega} \]

tips: 蒙特卡洛积分，要求对什么积分，就应该在该区域上采样.

现在已经在光源上采样，Lo积分能否转化为光源上的积分？

答案是可以. 只需要知道\(d\omega\)与\(dA\)关系. \(dA\)是光源上一个小面，\(d\omega\)是\(dA\)投影到物体表面单位球面上的一个立体角.

立体角定义：球面上单位面积/距离平方，即 \(d\omega=\frac{dA_x}{r^2}\)
注：\(dA_x\)是球面上的单位面积，r是球面半径.

参见：计算机图形：辐射度光照模型立体角

于是，我们将光源上的面积\(dA\)投影到球面上，即垂直于\(xx'\)连线，得到投影面积\(dAcos θ'\)

根据立体角定义，可知：

\[d\omega = \frac{dAcos θ'}{\lVert x'-x\rVert ^2} \]

重写渲染方程：

\[\begin{aligned} L_o(x,\omega_o) &= \int_{Ω^+}L_i(p,\omega_i)f_r(x,\omega_i,\omega_o)cos θ d\omega_i\\ &= \int_A L_i(x,\omega_i)f_r(x, \omega_i, \omega_o)\frac{cos θ cos θ'}{\lVert x'-x\rVert ^2}dA \end{aligned} \]

至此，可用蒙特卡洛积分来求解：

f(x): 积分项里所有东西，即\(L_i(p,\omega_i)f_r(x,\omega_i,\omega_o)cos θ\)
pdf: 1/A

之前，我们假设光线是通过“随机”的均匀采样物体表面的半球发射的. 现在考虑radiance来自2个部分：
1）光源 light source（直接光照 direct，光源采样，无需使用RR）；
2）其他反射（间接光照 indirect，RR）.

改进伪码：

shade(p, wo)
    // 1. Contribution from the light source
    Uniform sample the light at x' (pdf_light = 1/A)
    L_dir = L_i * f_r * cos θ * cos θ / |x' - p|^2 / pdf_light

    // 2. Contribution from other reflectors
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    If ray r hit a non-emitting object at q
        L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR
    
    Return L_dir + L_indir

之前假设光源和物体之间无障碍物，如果光源被挡住呢？

可以从物体表面发射一条光线，检查中间是否被其他物体挡住. 如果没被挡住，才计算直接光照对应的L_dir.

伪代码可做如下修改：

// Contribution from the light source
L_dir = 0.0
Uniformly sample the light at x' (pdf_light = 1/A)
Shoot a ray from p to x'
If the ray is not blocked in the middle
    L_dir = ...

如下图，真实照片（左）与路径追踪渲染效果（右）对比：

from: The Cornell box — http://www.graphics.cornell.edu/online/box/compare.html

可见，路径追踪效果与真实照片几乎一模一样.

小结

ray tracing概念

以前的ray tracing == Whitted-style ray tracing

现代的ray tracing指所有光线传播方法的大集合：

1）(单向/双向)path tracing
2）光子映射(Photon mapping)
3）梅特罗波利斯光传输(Metropolis light transport)
4）VCM(结合双向路径追踪 + 光子映射) / UPBP(结合了所有方法)

未解决问题

均匀采样半球

给定一个半球，如何进行均匀采样？如何对任意函数进行采样？

蒙特卡洛积分允许任意pdf

那么，什么样的pdf是最佳选择呢？针对某种形状，进行最好的采样方法.

如何控制随机数的距离？

均匀采样不只是确保随机数均匀分布在随机空间内，它们的距离也能控制很好，不会相对聚集或分散，这种随机数序列，叫低差异序列（low discrepancy sequences）.

同时对半球和光源采样，能结合它们，实现更好效果？

multiple imp. sampling（MIS），目前学术界的前沿研究热点.

为什么像素的radiance是通过它的所有光线的radiance的平均值？靠近像素中心部分，权重能否更高些？

pixel reconstruction filter

计算得到的是像素的radiance，如何得到像素的颜色呢？

gamma correction（gamma校正），中间会涉及到curves，color space（颜色空间）.

参考

GAMES101 lecture 16

posted @ 2025-05-30 23:06 明明1109 阅读(141) 评论(0) 收藏举报

刷新页面返回顶部

明明1109