计算机图形：辐射度光照模型

目录

辐射度光照模型

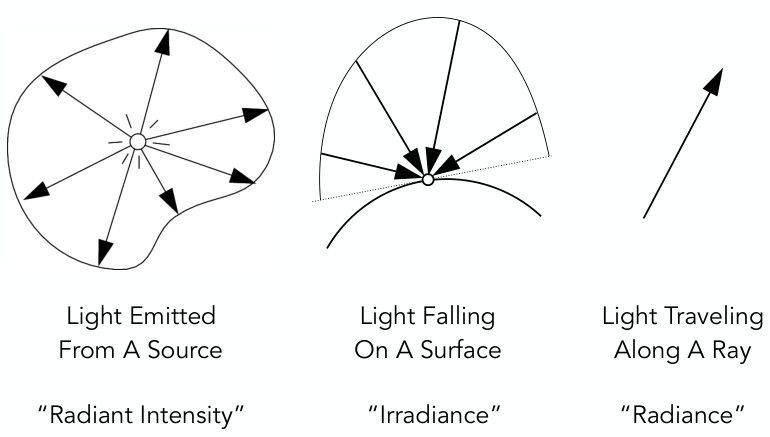
基本光照模型（Blinn-Phong光照模型）的局限：不能对一些光照效果进行精确描述.

为此，辐射度量学（Radiometry）提出辐射度模型（radiosity model）：分析辐射能在物体表面之间的转移和能量守恒定律，从而准确地建立物体表面的漫反射模型.

术语

光的量子模型中，光的辐射能量由光子（photon）携带. 对于单色光线，每个光子能量：

\[E_{photon,f}=hf[J=Joule] \]

其中，频率f，表示光的颜色特征（\(\lambda=c/f\)，\(\lambda\)波长，c光速）；h普朗克常数，\(h=6.6262\times 10^{-34}J\cdot s\).

单色光辐射能总能量：所有相同频率的光子的能量

\[E_f=\sum_{all\space photons}hf[J=Joule] \]

光谱辐射能（Spectral Radiance）Q：一个具体的光频率的辐射能量. 任何实际的光辐射，都是一个频率范围（非单个频率）. 总辐射能，是所有频率的全部光子的和

\[Q=E=\sum_{f}\sum_{all\space photons}hf[J=Joule] \]

光通量（Radiant Flux）\(\phi\)，也称光能（Radiant Power, power）：单位时间传递（发射、反射、传输或接收）的辐射能总量

\[\phi=\frac{dQ}{dt} [W=Watt][lm=lumen] \]

注：W（瓦特）=j/s（焦/秒），lm=lumen（流明）

光强度（Intensity）I是在特定方向、单位立体角、单位投影面积的光通量的度量，单位：\(W/(m^2 \cdot sr)\)(sr是立体角单位，球面度). 有时，也指特定方向的光通量.

辐射强度（Radiant Intensity）：点光源在单位立体角发射的光能（power）.

\[I(\omega)=\frac{d\phi}{d\omega}[\frac{W}{sr}][\frac{lm}{sr}=cd=candela] \]

img

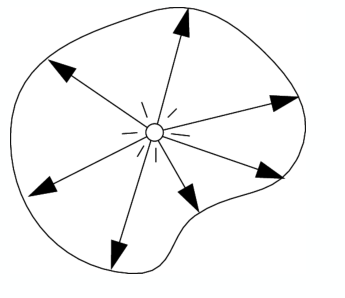
注：candela是发光强度的单位，7个SI基本单位之一. 1坎=1流明/球面度.

立体角（Solid Angle）：球面对向面积与半径的平方的比.

\[Ω=\frac{A}{r^2}[sr] \]

注：sr是立体角单位，球面度.

辐照度（Irradiance）：物体表面一点单位面积的入射光能（power）.

\[E(x)=\frac{d\phi}{dA}[\frac{W}{m^2}][\frac{lm}{m^2}=lux] \]

立体角Ω

球面坐标系中，球面的任意极小区域dA可看做矩形

∴\(dA\)面积：\(dA=(rd\theta)(r\sin \theta d\phi)=r^2\sin\theta d\theta d\phi\)

极小立体角：\(d\omega=\frac{dA}{r^2}=\sin\theta d\theta d\phi\)

对极小立体角做曲面积分，可得立体角：

\[Ω=\iint_Sdω=\iint_s\sin\theta d\theta d\phi \]

img

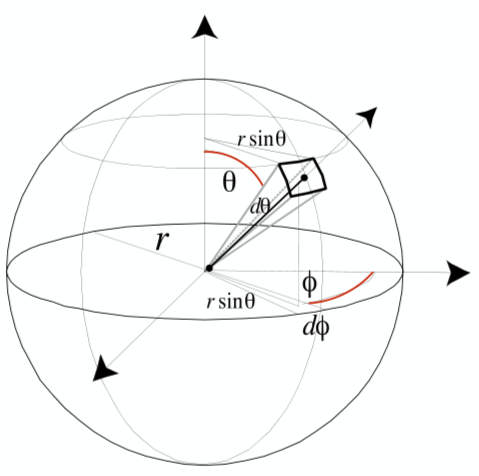
完整球面对球内任一点立体角4π sr：

\[\oiint_S d\omega=\oiint_S\sin\theta d\theta d\phi = \int_0^π \sin\theta d\theta\int_0^{2π}d\phi=[-\cos\theta]_0^π (2π)=4π \]

该结论对所有封闭曲面都成立，是高斯定律的主要依据.

几个概念的简单区别：

  • 辐射强度（Radiant Intensity）：点光源向四周辐射光能的强度
  • 辐照度（Irradiance）：物体表面一点单位面积的入射power
  • 辐射度（Radiance）：光线沿着某个方向，在单位立体角、单位面积上传输的power

img

辐照度（Irradiance）

img

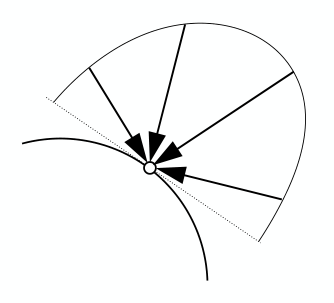
前面知道，Irradiance定义：物体表面单位面积的入射power. 设物体表面面积为\(A\)，可知Irradiance公式：

\[E(x)=\frac{\phi(x)}{A} [\frac{W}{m^2}] [\frac{lm}{m^2}=lux] \]

微分形式：

\[dE(x)=\frac{\phi(x)}{dA} \]

考虑光线以不同角度入射：

img

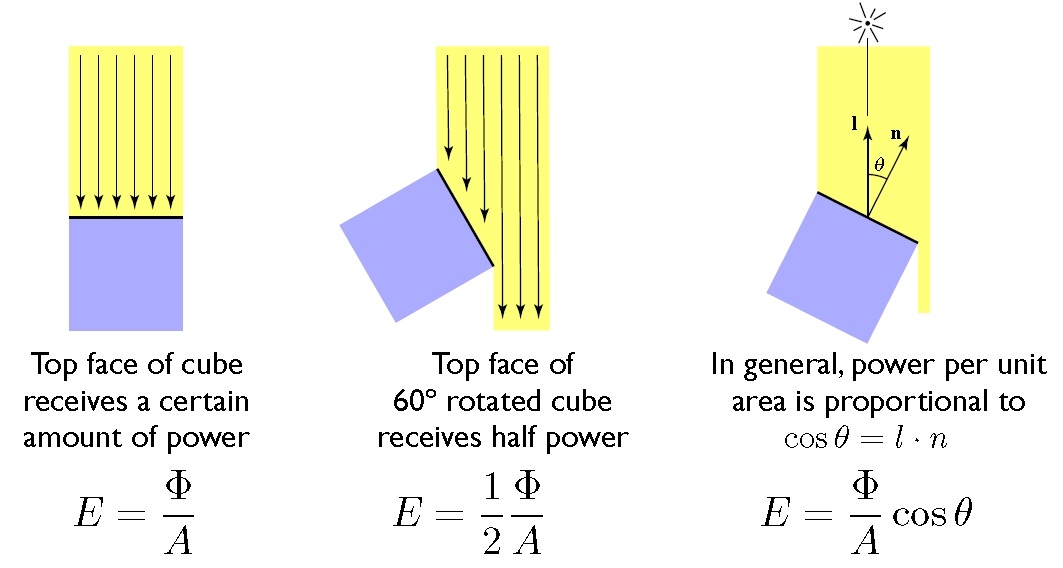
两种理解方式：
1）光的分量\(\phi cosθ\)垂直入射面A

\[E=\frac{\phi cosθ}{A} \]

2）光垂直入射面A的等效面\(A/cosθ\)

\[E=\frac{\phi}{A/cosθ}=\frac{\phi cosθ}{A} \]

而\(cosθ=\bm{l}\cdot \bm{n}\)（\(\bm{l}\)指向光源的单位向量，\(\bm{n}\)物体表面单位法向量）

朗伯余弦定律（Lambert's Consine Law）

朗伯余弦定律（Lambert's Consine Law）：
Blinn-Phong光照模型中，物体的漫反射光强与观察方向夹角的余弦成正比：

\[I(\theta)=I_N\cos \theta \]

其中，\(I(θ)\)表示面元(\(dA\))观察方向的漫反射光强度，\(I_N\)法线方向的漫反射光强度，\(θ\)观察方向与法线方向的夹角

该定律表明：观察方向与法线夹角越大，光强越小. 参见计算机图形：光照模型

从辐射度量学角度看，将入射光线分解到与面元垂直、平行的2个方向上，只有垂直分量才会被有效反射

∴有效Irradiance：\(E'=\frac{E\cos\theta}{A},E=\phi\).

二者公式相似，但又有区别：

朗伯余弦定律描述了漫反射表面的光强分布，而辐照度Irradiance描述单位面积接收的光功率.

Irradiance 衰减

Blinn-Phong模型中，为什么距离点光源越远，光强越弱（与距离平方成反比）？

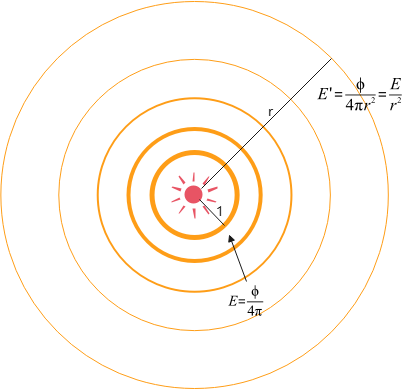
可用Irradiance解释. 假设点光源辐射的power为\(\phi\)，点光源往各个方向辐射的能量是均等的，能量传播过程中，其分布模型如下图，在一个个球面上.

那么，距离点光源为1的球面一点Irradiance：\(E=\frac{\phi}{S_{r=1}}=\frac{\phi}{4π}\)；

距离为r时，根据能量守恒，球面总能能量不变（\(\phi\)不变），故球面一点Irradiance：\(E'=\frac{\phi}{S_{r}}=\frac{\phi}{4πr^2}=\frac{E}{r^2}\)

可知，Irradiance与到光源距离\(r^2\)成反比.

img

辐射度（Radiance）

Radiance (luminance)：在单位立体角、单位投影面积的power. 方向可以是表面发射、反射、传输或接收的. 它描述了光源或表面在特定方向上的光能分布.

Radiance属性：

1）Radiance 描述了光线在环境中分布的属性

  • Radiance 是与光线有关的量
  • 渲染就是计算Radiance

2）Radiance沿着光线是恒定的（真空中）

3）针孔相机（Pinhole Camera）可测量Radiance

Radiance定义公式：

\[L(p,\omega)=\frac{d^2\phi(p,\omega)}{d\omega dA\cos\theta} [\frac{W}{srm^2}] [\frac{lm}{srm^2}=nit] \]

其中，\(\phi\)表示Radiant Flux，\(\omega\)表示立体角（Solid Angle），\(dA\cos\theta\)表示面元\(dA\)的投影面积.

img

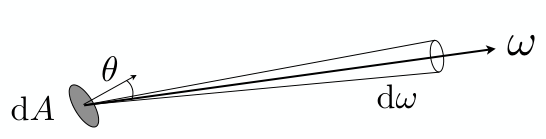
物体表面A的投影面积为\(A\cos\theta\)：

img

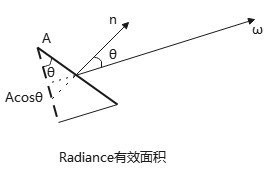
入射Radiance与Irradiance
Incident Radiance: 面元\(dA\)会在多个方向接收到光能，沿着固定方向\(\omega\)接收的Irradiance就是Radiance.

\[L(p, \omega)=\frac{dE(p,\omega)}{d\omega \cos \theta} \]

img

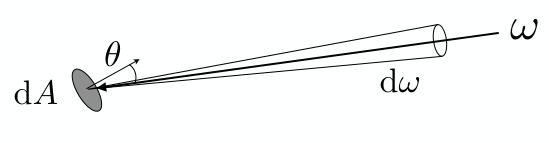
出射Radiance与Intensity
Exiting Radiance: 面元\(dA\)会往多个方向发射光能，离开单位投影面积的intensity就是Radiance.

\[L(p,\omega)=\frac{dI(p,\omega)}{dA\cos \theta} \]

img

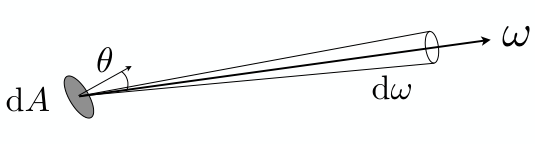
Radiance与Irradiance

两者都描述接收power时，区别：

  • Irradiance：面元\(dA\)接收的总power，即来自四面八方的Radiance；
  • Radiance：面元\(dA\)区域接收的来自特定方向\(\omega\)、立体角\(d\omega\)的power；

img
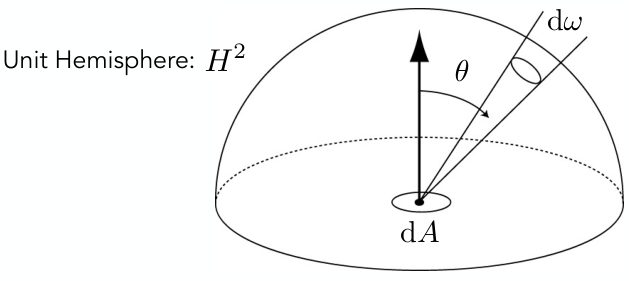
注：Unit Hemisphere 意为半球

i.e. Radiance属于Irradiance中特定方向接收的power

\[dE(p,\omega)=L_i(p,\omega)\cos\theta d\omega \]

由极小立体角定义知，\(d\omega=\sin\theta d\theta\phi\)

反过来，所有方向的Radiance积分就是Irradiance：

\[E(p)=\int_{H^2}dE(p,\omega)=\int_{H^2}L_i(p,\omega)\cos\theta d\omega \]

其中，\(H^2\)表示半球，\(L_i(p,\omega)\)表示方向\(\omega\)的Radiance，\(\theta\)表示\(\omega\)与法向量夹角.

最简单情况：如果是一个均匀半球，那么可以计算Irradiance如下

\[\begin{aligned} E(p)&=\int_{H^2}Ld\omega\\ &=L\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\cos\theta \sin\theta d\theta d\omega\\ &=L\pi \end{aligned} \]

双向反射分布函数（BRDF）

BRDF定义

一束光照射到物体表面会反射到各个方向，如何描述反射光线的分布特性？

以平面任一点p的反射为例：
来自方向\(\omega_i\)的入射Radiance转化为面元\(dA\)接收的power E（irradiance），power E会反射到其他任意方向\(\omega_o\).

对于固定反射方向\(\omega_r\)，power E的贡献有多少？这就是双向反射分布函数（Bidirectional Reflectance Distribution Function，BRDF）所描述的事情.

img

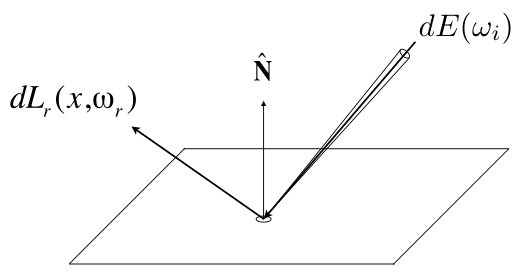
入射irradiance的微分：\(dE(\omega_i)=L_i(\omega_i)\cos\theta_i d\omega_i\)；

出射radiance微分（由\(dE(\omega_i)\)贡献）：\(dL_r(\omega)\)

img

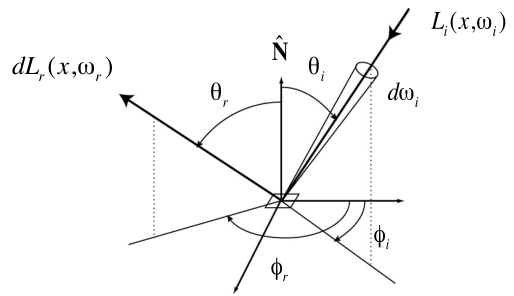
由方向\(\omega_i\)入射的光，会反射到各个方向. 而BRDF表示每个出射方向\(\omega_r\)中，可描述有多少来自入射方向\(\omega_i\). 于是，BRDF可这样描述：

\[\begin{aligned} f_r(\omega_i \rightarrow w_r) &= \frac{dL_r(\omega_r)}{dE_i(\omega_i)}=\frac{dL_r(\omega_r)}{L_i(\omega_i)\cos\theta_i d\omega_i}\space [\frac{1}{sr}] \end{aligned} \]

为什么用出射Radiance除以入射Irradiance？

因为\(\omega_i\)方向的入射光只有部分反射到\(\omega_r\)方向，而要描述该入射光线的反射分布特性，就需要用“部分/整体”，即“出射radiance/入射irradiance”.

反射方程（Refection Equation）

img

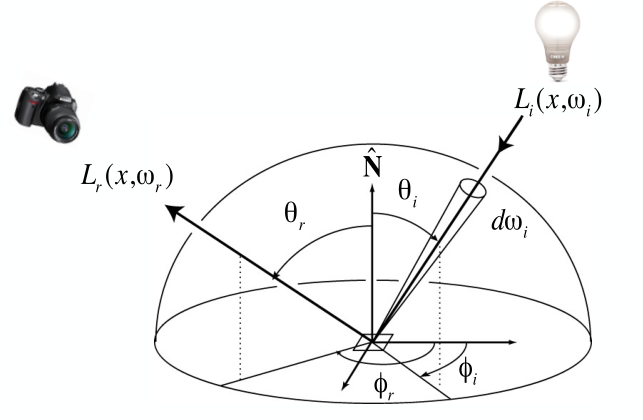
上面模型中，每束入射到面元\(dA\)的光线会反射到各个方向，i.e. 方向\(\omega_r\)的出射光线来自各个方向的入射光线，而入射方向\(\omega_r\)只贡献了一部分. 如何计算出射方向\(\omega_r\)的radiance？
根据BRDF，对每个入射方向对出射方向\(\omega_r\)贡献的radiance求积分即可.

p点反射方程：

\[L_r(p,\omega_r)=\int_{H^2}f_r(p,\omega_i\rightarrow \omega_r)L_i(p,\omega_i)\cos\theta d\omega_i \]

其中，p代表感兴趣的点，\(H^2\)表示半球中所有方向. \(L_i(p,\omega_i)\)表示来自光源的\(\omega_i\)方向的入射radiance，\(L_r(p,\omega_r)\)表示沿着\(\omega_r\)方向的出射radiance.

渲染方程（Rendering Equation）

img

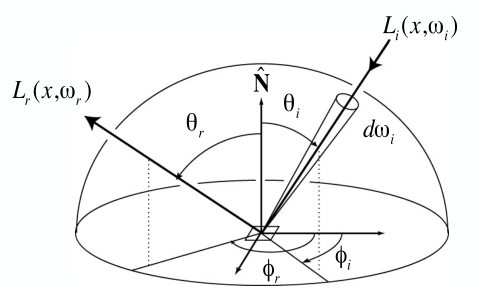
光线追踪模型中，如果要考虑某个着色点光照，就需要考虑所有能入射的光线. 但是，能到达该点的光线，除了光源，还有其他物体的反射光线.

于是，反射方程中，一个面元的\(L_r(p, \omega_r)\)可能作为另一个的\(L_i(p,\omega_i)\)，也就是存在递归问题：

img

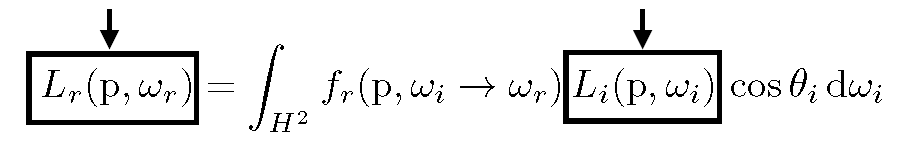
由于物体本身可作为光源，可修改反射方程，得出p点渲染方程：

\[L_o(p,\omega_0)=L_e(p,\omega_o)+\int_{Ω^+}f_r(p,\omega_i\rightarrow \omega_o)L_i(p,\omega_i)(\bm{n}\cdot \bm{\omega_i}) d\omega_i \]

其中，\(L_o\)表示出射radiance，\(L_e\)表示作为光源辐射的radiance，p是感兴趣的点，\(\omega_o\)反射方向，\(Ω^+\)表示上半球中所有方向，\(f_r\)表示BRDF函数，\(L_i\)表示入射radiance，\(\omega_i\)表示入射方向，\(\bm{n}\cdot \bm{\omega_i}\)表示法向量与入射方向的夹角的余弦.

渲染方程中，
未知量：\(L_o(p,\omega_o), L_i(p,\omega_i)\)；
已知量：\(L_e(p,\omega_o), f_r(p,\omega_i\rightarrow \omega_o), (\bm{n}\cdot \bm{\omega_i}), d\omega_i\)

理解渲染方程

  • 对于反射方程

img

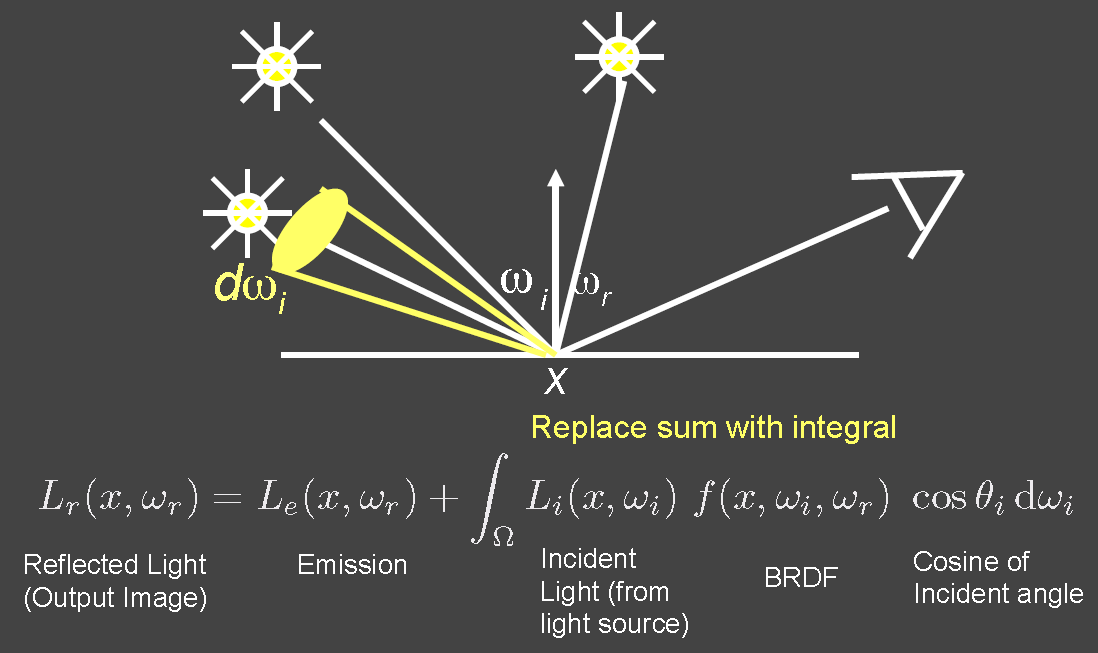
计算反射radiance时，多个点光源的贡献，可以用求和；面光源的贡献，可以用积分.

\[\begin{aligned} 求和：L_r(x,\omega_r) &= L_e(x,\omega_r)+\sum L_i(x,\omega_i)f(x,\omega_i,\omega_r)cos θ_i\\ 积分：L_r(x,\omega_r) &= L_e(x,\omega_r)+\int_ΩL_i(x,\omega_i)f(x,\omega_i,\omega_r)cos θ_i d\omega_i \end{aligned} \]

  • 对于渲染方程

img

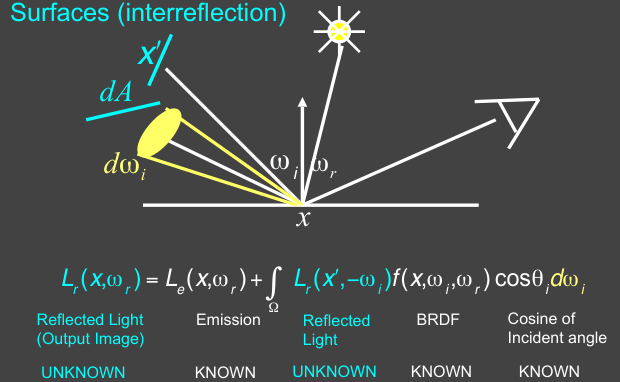
真实场景中，物体表面一点\(x\)入射光线可能包括：

1）点光源发射的光;
2）面光源发射的光，可看作多个点光源发射的光;
3）另一个物体表面\(x'\)反射的光;

点\(x\)的入射radiance，依赖于其他点辐射的radiance. 于是，这3点可概括为由面元\(dA\)位置\(x'\)处沿\(-\omega_i\)方向发射、立体角\(d\omega_i\)的光线，其出射radiance为积分项：

\[\int_ΩL_r(x',-\omega_i)f(x,\omega_i,\omega_r)\cos\theta_i d\omega_i \]

注：方向\(\omega_i\)指从点\(x\)指向点\(x'\)。

于是，渲染方程可写成统一形式：

\[L_r(x,\omega_r)=L_e(x,\omega_r)+\int_ΩL_r(x',-\omega_i)f(x,\omega_i,\omega_r)\cos\theta_i d\omega_i \]

求解渲染方程

img

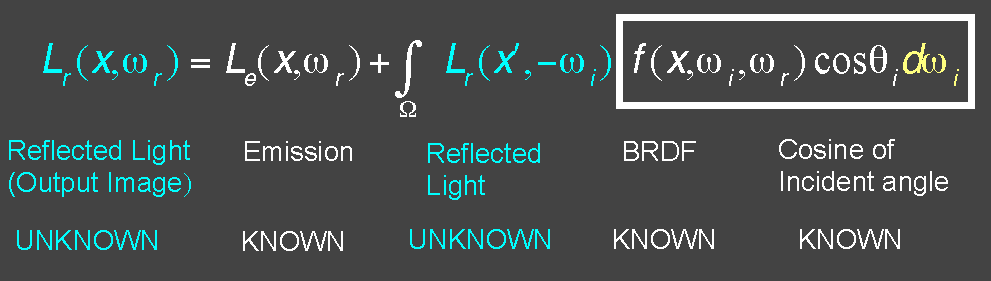
渲染方程中，已知量：

  • \(L_e(x,\omega_r)\) 作为光源辐射到点\(x\)的radiance；
  • \(f(x,\omega_i,\omega_r)\cos\theta_i d\omega_i\) 可通过定义物体材质得到.

未知量：

  • \(L_r(x,\omega_r)\) 点\(x\)反射的radiance
  • \(L_r(x',-\omega_i)\) 从其他物体点\(x'\)反射到\(x\)的radiance

简化形式（第二类Fredholm integral equation）：

\[\bm{I(u)}=e(u)+\int \bm{I(v)}K(u,v)dv \]

继续简化，写成算子形式：

\[\bm{L}=E+K\bm{L} \]

通过简写形式，求解渲染方程：

\[\begin{aligned} \bm{L} &= E+K\bm{L}\\ I\bm{L}-K\bm{L} &= E\\ (I-K)\bm{L} &= E\\ \bm{L} &= (I-K)^{-1}E \end{aligned} \]

再由二项式定理（binomial theorem）：

\[\bm{L}=(I+K+K^2+K^3+...)E\\ \bm{L}=E+KE+K^2E+K^3+... \]

各分解项意义：

  • \(E\) 直接由光源辐射的能量
  • \(KE\) 光源辐射的能量经1次反射后的能量（直接光照）
  • \(K^2E\) 经2次反射后的能量（间接光照）
  • \(K^3E\) 经3次反射后的能量
  • 依次类推

蒙特卡洛积分

先回顾一些概率论知识.

随机变量

  • \(X\)，随机变量，代表可能值的分布；
  • \(X\sim p(x)\)，概率密度函数（probability density function，PDF），描述随机过程中选择值x的可能性.

均匀分布PDF中，所有值可能性一样. 例如，掷骰子，掷出的骰子值\(X\)是一个随机变量，取值1,2,3,4,5,6. 有，

\[p(1)=p(2)=p(3)=p(4)=p(5)=p(6) \]

概率

随机变量取某个值的可能性，称为概率.

n个离散值\(x_i\)，对应概率\(p_i\). 概率分布要求：

\[p_i\ge 0\\ \sum_{i=1}^np_i=1 \]

期望

取每个值，都有一个可能性. 如果取一个值，会取到什么值？

这就是\(X\)的期望：

\[E[X]=\sum_{i=1}^nx_ip_i \]

对于掷骰子的例子，

\[E[X]=\sum_{i=1}^6\frac{i}{6}=(1+2+3+4+5+6)/6=3.5 \]

概率密度函数

对于随机变量连续的情况，如何描述其概率、期望？

可以用概率密度函数（PDF）．

img

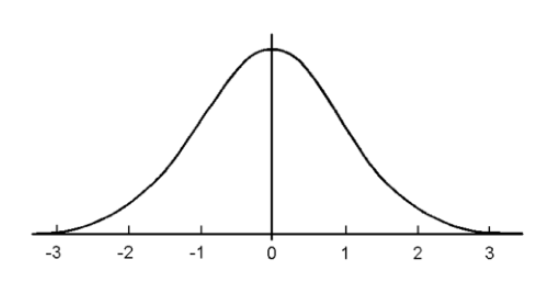
\(X\sim p(x)\)，那么概率密度函数p(x)，满足性质：

1）\(p(x)\ge 0, \int p(x)dx = 1\)；
2）\(E[X]=\int xp(x)dx\)

*　复合随机变量

如果有另一个随机变量\(Y\)，是\(X\)的函数：

\[X\sim p(x)\\ Y=f(X) \]

那么，\(y=f(x),p_y(y)=p(x)\)，而Y的期望：

\[E[Y]=E[f(X)]=\int yp_y(y)dy = \int f(x)p(x)dx \]

蒙特卡洛积分（Monte Carlo Integration）

对于任意函数\(f(x)\)，如何求定积分\(I=\int_{a}^bf(x)dx\)？

img

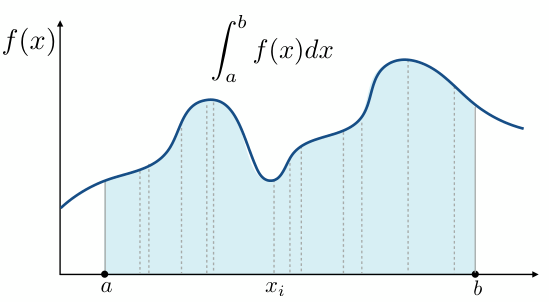
方法一：求出\(f(x)\)的原函数\(F(x)\)，即\(F'(x)=f(x)\)，然后\(I=F(b)-F(a)\).

方法二：不是每个函数都能求出原函数，可用蒙特卡洛积分法近似求解任意积分.

将区间\([a,b]\)均匀分为\(N\)个子区间，每个宽度\(\Delta x=\frac{b-a}{N}\)，将\(N\)个矩形面积求和，得到积分区间近似值. 当\(N\)越大，求和值越接近\(I\).（黎曼积分）

\[I\approx\sum_{i=1}^Nf(x_i)\Delta x=\frac{b-a}{N}\sum_{i=1}^Nf(x_i) \]

换一种理解方式：采样思想.
从\([a,b]\)中采样\(N\)个\(x_i\)，每个采样点对应一个以\(f(x_i)\)为高、\(b-a\)为宽的矩形，\(N\)个矩形面积的均值近似等于积分区间面积

\[I\approx\frac{1}{N}\sum_{i=1}^Nf(x_i)(b-a)=\frac{b-a}{N}\sum_{i=1}^Nf(x_i) \]

这就是蒙特卡洛积分的基本思想，可通过改变采样方式和采样频率，从而改善采样结果.

对于上面的采样，其实是一种均匀分布采样：\(X\sim p(x)=C,C=\frac{1}{b-a}\)，\(C\)是常量

∴

\[I\approx\frac{1}{N}\sum_{i=1}^N\frac{f(x_i)}{p(x_i)} \]

上面是均匀采样结果，而对于通用的采样，只需要\(X_i\sim p(x)\)，就得到蒙特卡洛积分公式：

\[\int f(x)dx = \frac{1}{N}\sum_{i=1}^N \frac{f(X_i)}{p(X_i)},X_i\sim p(x) \]

由大数定律，样本数\(N\)越多时，算术平均值越接近于期望值.
令\(h(x)=\frac{f(x)}{p(x)}\)

\[E_{X\sim p}[h(x)]=\lim\limits_{N\to ∞}\frac{1}{N}\sum_{i=1}^Nh(x_i)\approx \frac{1}{N}\sum_{i=1}^Nh(x_i) \]

也就是说，\(I\)值就是\(h(x)\)的期望值.

将该形式拓展到连续的情况：

\[E_{X\sim p}[h(x)]=\int_{}h(x)p(x)dx=\int_{}f(x)dx=I \]

可以将p换成任意形式分布，不一定是均匀分布.

参考

GAMES101 lecture 15

立体角 | wiki

兰伯特光照模型（漫反射）

posted @ 2025-05-21 19:20  明明1109  阅读(127)  评论(0)    收藏  举报