计算机图形：材质和外观

目录

• 基本概念
• 材质
  • 漫反射材质
  • Glossy material材质
  • 反射、折射材质
    • 反射
    • 折射
  • 菲涅⽿项
    • 计算菲涅尔项
  • 微表面材质
    • 微表面概念
    • 微表面BRDF
  • 各项同性/各项异性材质
    • 各项异性BRDF
  • BRDF性质
  • 测量BRDF
• 参考

基本概念

• 材质与外观

不同的材质（Material）在不同的光线作用下，表现出不同的外观（Appearance）. 外观是 材质 + 光线 共同作用结果.

材质的研究话题：不同的光照和不同的材质的作用方式.

• 材质与纹理

之前提到过纹理（Texture）（参见计算机图形：纹理与表面细节），也能决定物体外观，与材质区别是什么？

材质是物体表面光学属性集合，决定了光如何与表面交互；

纹理是图像或数据贴图，用于为材质提供具体的细节图案或参数分布.

主要区别：

特性	材质（Material）	纹理（Texture）
本质	光学属性的抽象参数（如“塑料”“金属”）	具体的图像或数据贴图（如“木纹图片”）
作用层级	定义整体表面行为（光如何反射/折射）	为材质提供局部细节或参数变化
依赖关系	可以独立存在（仅用数值）	通常服务于材质（作为输入）
示例	PBR材质、Phong材质	漫反射贴图、法线贴图

材质

材质Material == BRDF

漫反射材质

下图是一个漫反射材质（Diffuse Material），入射光线会均匀地反射到各个方向.

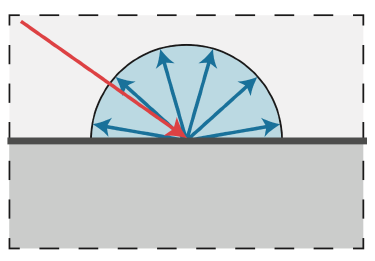
漫反射材质也称朗伯材质（Lambertian Material）. 假设入射光是均匀的（uniform），并且材质本身不会发光.

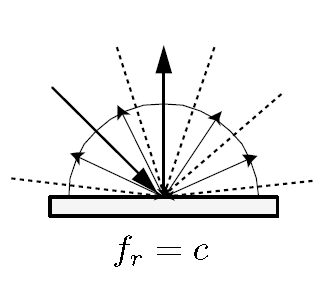
因为入射光是均匀的，所以入射radiance \(L_i(\omega_i)\)是一样的

根据渲染方程，有，

\[\begin{aligned} L_o(\omega_o) &= \int_{H^2}f_rL_i(\omega_i)cos θ_i d\omega_i\\ &= f_rL_i\int_{H^2}cos θ_id\omega_i\\ &= \pi f_r L_i\\ f_r &= \frac{ρ}{\pi}, ρ=\frac{L_o(\omega_o)}{L_i}\in [0,1] \end{aligned} \]

于是，我们可以定义反射率\(ρ\in [0,1]\)，进而求得BRDF \(f_r\).

为什么定积分\(\int_{H^2}cos θ_id\omega_i = \pi\)？

\[\begin{aligned} d\omega &= sin θdθ d\phi\\ \int_{H^2}cos θd\omega &= \int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}} cos θ sin θdθ d\phi\\ &= \frac{1}{2}\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}sin 2θ dθ d\phi\\ &= \frac{1}{4}\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}sin 2θ d2θ d\phi\\ &= \frac{1}{4}\int_{0}^{2\pi}\int_{0}^{\pi}sin t dt d\phi\\ &= \frac{1}{4}\int_{0}^{2\pi}(-cos t)\biggm\vert_0^\pi d\phi\\ &= \frac{1}{4}\int_{0}^{2\pi} (-cos \pi + cos 0) d\phi\\ &= \frac{1}{4}\int_{0}^{2\pi} 2 d\phi\\ &= \pi \end{aligned} \]

Glossy material材质

一条入射光线，会被反射到一个角度范围，但又不是镜面反射，表面比镜子粗糙.

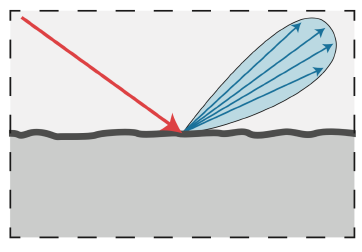
这种材质，就是Glossy material，即抛光金属材质.

例如，下图左是铜，右是铝：

反射、折射材质

部分能量反射出去，部分进入物体内部，发生折射. 这类常见材质，如玻璃、水.

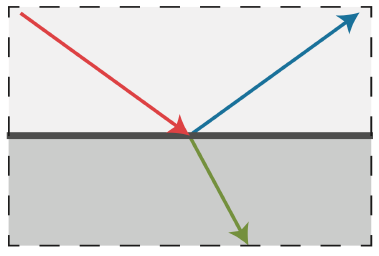
例如，下图左模拟水材质，右模拟玻璃材质：

反射

理想镜面反射：能量被全部反射出去，反射角=入射角

注意立体角定义\(d\omega=sin θdθd\phi\)，有两种方式来考察反射角与入射角：

1）反射定律，与法线角度\(θ\)相关

∵\(θ=θ_o=θ_i\)
∴\(\vec{n}\)（单位法向量）是\(\omega_o, \omega_i\)角平分线

用平行四边形法则：

两个向量合成时，以表示这两个向量的线段为邻边作平行四边形，这个平行四边形的对角线就表示合向量的大小和方向，这就叫做平行四边形定则（Parallelogram law）

\(\omega_o + \omega_i = 2cos θ\space \vec{n} = 2(\omega_i \cdot \vec{n})\vec{n}\)

∴\(\omega_o = -\omega_i + 2(\omega_i \cdot \vec{n})\vec{n}\)

2）俯视图（从上往下看），与\(\phi\)相关

入射光线与反射光线是相反的：

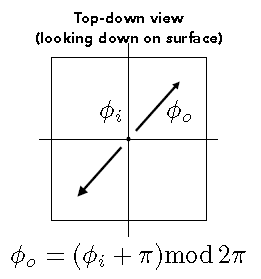
反射光对应的\(\phi_o\)，入射光对应\(\phi_i\)，它们关系：

\[\phi_o = (\phi_i + \pi) mod 2\pi \]

折射

除了在物体表面发生反射，光线还可能穿透表面传输，这就是折射.

当光线进入新介质时，会发生折射现象.

类似于反射，同样2个方面考虑折射角度：

1）折射定律（Snell定律）

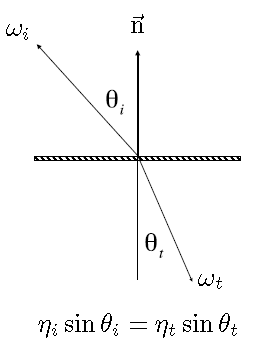
折射角\(η_t\)与入射角\(η_i\)关系如下：

\[η_i sin θ_i = η_t sin θ_t \]

其中，\(η_i,η_t\)分别是入射材料的折射率、折射材料的折射率

\[φ_t = φ_i ± \pi \]

下表是常见材质的折射率：

Medium	中文名	η*
Vacuum	真空	1.0
Air (sea level)	空气	1.00029
Water (20°C)	水	1.333
Glass	玻璃	1.5-1.6
Diamond	钻石	2.42

注：*代表折射率跟波长相关，这里是取平均值.

参见：计算机图形：光照模型

2）俯视图

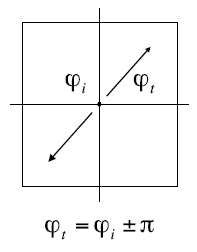
• 求解折射角

已知\(η_i,η_t,θ_i\)，根据折射定律，可求得折射角\(θ_t\)：

\[\begin{aligned} η_i sin θ_i &= η_t sin θ_t\\ cos θ_t &= \sqrt{1-sin^2 θ_t}\\ &= \sqrt{1- (\frac{η_i}{η_t})^2 sin^2 θ_i}\\ &= \sqrt{1- (\frac{η_i}{η_t})^2 (1-cos^2 θ_i)} \end{aligned} \]

为什么要计算余弦，而不是直接用正弦？

因为\(cos θ_t\)只要计算出一个有意义的实数，就能得到\(θ_t\). 如果得不到有意义的实数，说明不可能发生折射.
而用直接用正弦没有这一点.

什么时候没有意义？

根号里面值 < 0，即\(1- (\frac{η_i}{η_t})^2 (1-cos^2 θ_i) < 0\). 此时，

\[\frac{η_i}{η_t} > 1 \]

只有从更密的介质到更疏的介质，才会发生这种现象.

如下图所示，在水中往上看，只能看到一个很小的锥形区域（接近90°入射）. 只要入射角度一大，就发生反射，无法发生折射.

菲涅⽿项

菲涅尔反射 或 菲涅⽿项（Fresnel Reflection / Term）指光线照射物体表面时，反射、折射与观察角度之间的关系. 当观察者视线方向与物体法线的夹角越大时，反射的光量越多；夹角越小时，反射的光量越少.

例，书桌靠近墙面，上面垂直放着一本书靠着墙，然后以不同视角观察桌面对书的反射.

会发现，几乎垂直观察桌面时，看不到对书的反射；几乎平行观察桌面时，会看到对书的反射特别明显.

光线照射到平面上，会分为反射、折射2个部分. 则有，

\(θ_i=\) 反射角 = 入射角

反射角：反射光线的方向（\(\bm{r_i}\)）与表面法线（\(\bm{n}\)）之间夹角；
入射角：入射光线（\(\bm{l}=-\bm{i}\)）与表面法线（\(\bm{n}\)）之间夹角.

可推导出，

\[\bm{r_i}=2(\bm{n}\cdot \bm{l})\bm{n}-\bm{l}\\ \iff \bm{r_i}+\bm{l}=2(\bm{n}\cdot \bm{l})\bm{n} \]

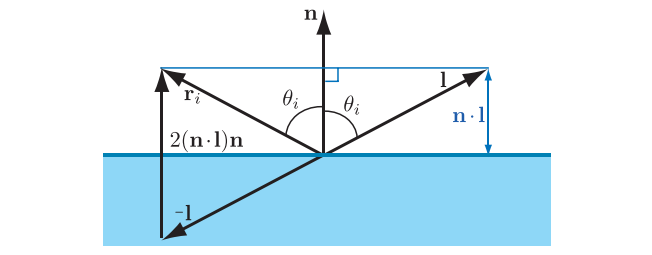
from RTR4th fig. 9.19

于是，可知，反射光的光量，可由菲涅尔反射率F来描述，它取决于入射角\(θ_i\).

下图展示一个绝缘体(Dielectric, \(η=1.5\)) 的菲涅⽿项：

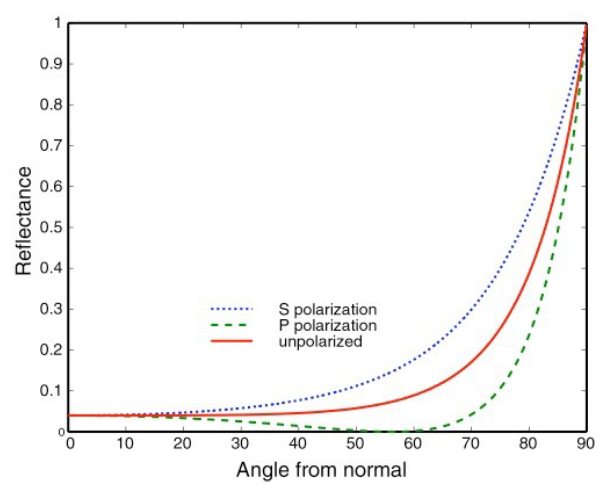
下图展示一个导体（Conductor）的菲涅⽿项：

反射率取决于入射角度和光的偏振（polarization of light）. 光的偏振状态分为s偏振、p偏振：

• s偏振（S polarization，垂直入射面振动）的反射率通常更高
• p偏振（P polarization，平行入射面振动）在布儒斯特角时可实现零反射

计算菲涅尔项

精确计算菲涅尔反射率，需要考虑极性（polarization）

对于绝缘体，反射率分为s偏振\(R_s\)、p偏振\(R_p\)，计算公式如下：

\[\begin{aligned} R_s &= \biggm\vert \frac{n_1cos θ_i - n_2cos θ_t}{n_1cos θ_i + n_2cos θ_t} \biggm\vert ^2 = \biggm\vert \frac{n_1cos θ_i - n_2\sqrt{1-(\frac{n_1}{n_2}sin θ_i)}}{n_1cos θ_i + n_2\sqrt{1-(\frac{n_1}{n_2}sin θ_i)}} \biggm\vert ^2\\ R_p &= \biggm\vert \frac{n_1cos θ_t - n_2cos θ_i}{n_1cos θ_t + n_2cos θ_i} \biggm\vert ^2 = \biggm\vert \frac{n_1\sqrt{1-(\frac{n_1}{n_2}sin θ_i)} - n_2cos θ_i}{n_1\sqrt{1-(\frac{n_1}{n_2}sin θ_i)} + n_2cos θ_i} \biggm\vert ^2 \end{aligned} \]

如果不考虑极性，可将它们平均，得到菲涅尔反射率：

\[F(θ_i)=R_{eff} = \frac{1}{2}(R_s + R_p) \]

由于\(R_s, R_p\)计算复杂，常用Schlick近似（Schlick’s approximation）菲涅尔反射率：

\[\begin{aligned} F(\bm{n}\cdot \bm{l}) &= F_0 + (1-F_0)(1-(\bm{n}\cdot \bm{l})^+)^5,\\ F_0 &= (\frac{n_1-n_2}{n_1+n_2})^2 \end{aligned} \]

注：\(x^+\)指最小值限定为0

微表面材质

微表面概念

微表面材质（Microfacet Material）是一种基于物理的材质.

微表面基于模型：当我们距离物体足够远，很多微小的东西看不到，最终能看到的是微小的东西对表面的作用，对光的影响形成的总体的效应.

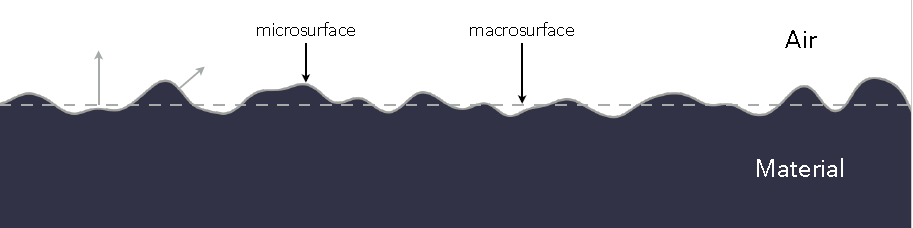
微表面原理：
从近处看，看到的是微观表面（microsurface），表面是凹凸不平的；从远处看，看到的是宏观表面（macrosurface），表面是平的、粗糙的.

对于粗糙表面：

• 从远处看（Macroscale）：平的，粗糙的
• 从近处看（Microscale）：凹凸不平的（bumpy），镜面反射（每一个微元）

表面各个微小元素像镜子，被称为微表面（Microfacets），每个微表面都有各自法线.

简而言之，微表面从近处看，看到的是几何；从远处看，看到的是材质或外观

微表面BRDF

如果将微表面法向量绘制出来，可以看到分布如下：

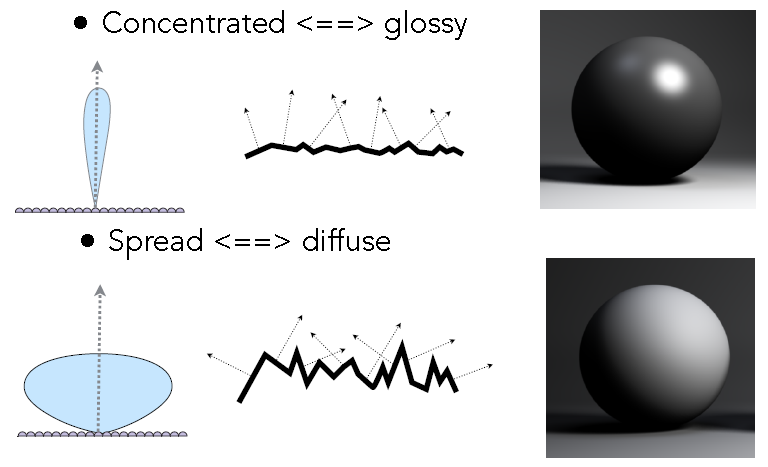
对于glossy材质，法向量会集中在一个很小的区域；对于漫反射材质（表面粗糙），法向量分布在一个比较大的区域.

微表面BRDF计算公式：

\[f(\bm{i}, \bm{o})=\frac{F(\bm{i}, \bm{h})G(\bm{i},\bm{o},\bm{h})D(\bm{h})}{4(\bm{n},\bm{i})(\bm{n},\bm{o})} \]

• \(\bm{i},\bm{o},\bm{h}\) 分别是入射向量，反射向量，半程向量
• \(F(\bm{i}, \bm{o})\) 菲涅尔项，如果入射光线几乎平行入射，那么大量光线被反射；
• \(D(\bm{h})\) 法线分布，在任何给定方向上，分布的值是多少；h是\(\omega_i,\omega_o\)的half vector（半程向量）；
• \(G(\bm{i},\bm{o},\bm{h})\) 几何项，用来修正：微表面之间可能会形成相互遮挡，从而产生阴影，视线无法观察到.

下图是一个微表面反射的示意图，光线从\(\omega_i\)到\(\omega_o\)是镜面反射：

\[\bm{h}=\frac{\bm{l}+\bm{v}}{\lVert \bm{l}+\bm{v} \rVert} \]

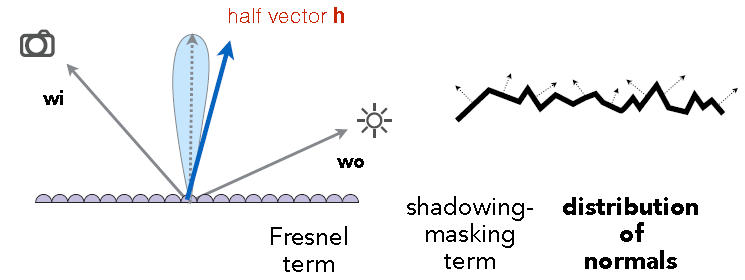
什么样的微表面，会把光线从入射方向\(\omega_i\)反射到出射方向\(\omega_o\)？

答：只有当它的法向量与half vector重合时.

什么时候最容易发生自遮挡？

答：当光线几乎平行入射物体表面，这种入射方向称为Grazing Angle（掠角）.

各项同性/各项异性材质

如果绘制出这两种材质法线贴图（R:x, G:y, B:z）和BRDF：

• 各项同性材质（Isotropic Materials）：各个方向法向量分布均匀，没有一定方向性；
• 各项异性材质（Anisotropic Materials）：法向量分布不均匀，有很明显方向性.

下图中，水平和竖直方向的法向量分布很明显不一样：

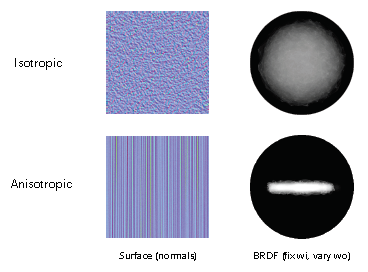
各项异性BRDF

反射取决于方位角\(\phi\). 如果BRDF在相同入射角度情况下，如果（绕法向量）旋转后不相同相同，那么称为各项异性BRDF（Anisotropic BRDF），对应材质称为各项异性材质；

反之，如果反射不取决于方位角，即旋转后的BRDF依然相等，称为各项同性BRDF（Isotropic BRDF），对应材质称为各项同性材质（Isotropic Materials）.

\[f_r(\theta_i,\phi_i;\theta_r,\phi_r)\neq f_r(\theta_i,\theta_r,\phi_r-\phi_i) \]

下图左 各向同性，形成一个高光圈；右 各向异性，形成扁平的高光圈.

下图是门把手和茶壶，各向异性还位于物体的不同位置

BRDF性质

• 非负性（Non-negativity）

\[f_r(\omega_i\to \omega_r) \ge 0 \]

• 线性（Linearity）

BRDF可拆成很多块，分别做光线传播，然后将结果加起来，与用整个BRDF计算得到的结果一样.

如，Blinn-Phong模型中，将环境光、漫反射、镜面反射分开计算后，将结果求和.

\[L_r(p,\omega_r) = \int_{H^2}f_r(p,\omega_i\to \omega_r)L_i(p,\omega_i)cos θ_i d\omega_i \]

• 可逆性（Reciprocity principle）

光路有可逆性，BRDF也同样有可逆性：交换入射、反射方向，BRDF值不变.

\[f_r(\omega_r\to \omega_i) = f_r(\omega_i\to \omega_r) \]

• 能量守恒（Energy conservation）

BRDF不会让能量变多. 场景中，光线弹射无数次后，虽然每次亮度会增加，但最终会收敛.

\[\forall \omega_r, \int_{H^2}f_r(\omega_i\to \omega_r)cos θ_i d\omega_i \le 1 \]

• 各向同性 vs 各向异性
  • 各向同性，BRDF只与相对方位角\(\phi_r - \phi_i\)有关：\(f_r(θ_i,\phi_i;θ_r,\phi_r)=f_r(θ_i,θ_r,\phi_r - \phi_i)\)
  • 由可逆性，交换入射、反射方向，\(f_r(θ_i,θ_r,\phi_r-\phi_i)=f_r(θ_r,θ_i,\phi_i-\phi_r)=f_r(θ_i,θ_r,|\phi_r-\phi_i|)\)

测量BRDF

为什么要测量BRDF？

测量得到的BRDF，可能会与图形学模型用到的BRDF不一样，因为模型是一种基于物理的近似，会忽略很多因素，以测量结果为准.

下图是各种方式得到的BRDF，其中绿色是测量得到：

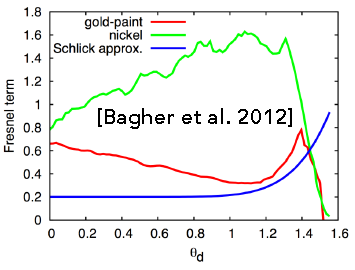
如何测量BRDF？

基于图像来测量. 基本思想是设置一个光源和相机，针对测试点，不断改变光源和相机位置（多组\(\omega_i,\omega_o\)），根据入射、反射光线求得BRDF.

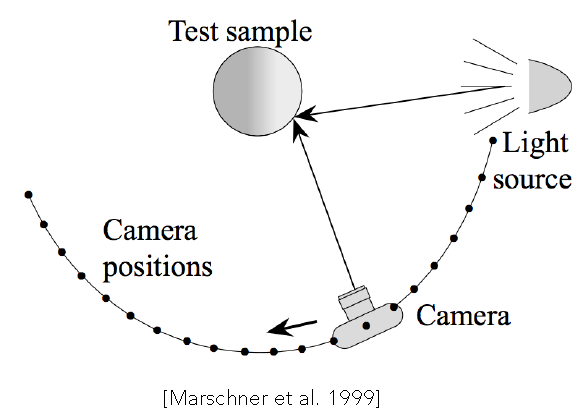
对于各向同性材质，只需要测量三维的\((θ_i,θ_o,|\phi_i-\phi_o|)\)；

一个有名的数据库项目是MERL BRDF Database，由三星和MIT与2004年开始合作建立，测量了很多材质BRDF，每个材质测量90 * 90 * 180次.

参考

Games101 Lecture 17