做题记录
写在前面:
感觉我有个毛病,写一段时间的题就会不自觉地减缓效率,有点摆烂(尤其晚上),写点总结吧,利用一下时间并养成好的习惯
2025/07/16
今天如几天常在楼下听 stntn 学长讲课,简单附属一下内容:
-
kruskal重构树:
挺简单的一个trick,对于一个关于树上特定边权的问题,可以先搞一遍最小生成树,排序从大到小的边权,通过并查集搞出一棵搜索树
这个搜索树性质是对于任意重构树叶子两点,原树上该两点的简单路径中边权最大值就是重构树的LCA的值
P1967 [NOIP 2013 提高组] 货车运输:
裸题,搞出重构树找LCA即可
P7834 [ONTAK2010] Peaks 加强版:
重构树向上找不超过x的LCA,在该LCA的子树上搞主席树求区间kth,码量挺大的,还没调出来(
P4768 [NOI2018] 归程:
在重构树定值LCA的子树结点上移动不需要花费,优化了时间
-
分层图最短路
挺版的,看到不好建边的时候,把后面的图拷贝一份,再将该点连向这张图,主要是让最短路好跑一些
P4568 [JLOI2011] 飞行路线
:看到免费的航线不好转移,考虑分层图,最多做10次免费飞机,把原图拷贝k次,每个点u有向下一层v的免费边,也有向这一层v的正常边,跑最短路即可
P3831 [SHOI2012] 回家的路:
网格图上只有特定点可以转向,考虑将网格变成只有横着走与只有竖着走两张图,特定点可从横向图转到竖向图/竖向图转到横向图,起点终点最短路,注意空间,所以要缩点,只存有用的点
-
2-SAT 问题
挺简单的,毕竟花时间自习过,对于各种\(0/1\)变量的共存问题,对每个必要状态连边,作tarjan找环,如果一点的两个状态在同一环上(又要存在,又要不存在),即可判断无解
P4782 【模板】2-SAT:
真的纯板子,就按照上方说法写就完了
CF1697F Too Many Constraints
每个点拆成多个bool变量,然后建边即可,重要的是要看出来要用2-SAT 解决
-
建图优化
讲了个前缀和优化建图,没听大明白,但网上好像没有讲这个的,感觉不是很重要,先搁置吧,挂个例题P6378 [PA 2010] Riddle
还有个线段树优化建图,把板子敲了,挺版的(CF786B Legacy
-
总结
题见少了,调代码跳少了,一道蓝题卡了半个下午,发现只是小错误(
2025/07/17
怎么上午就开始总结了(汗
如常上午 stntn 讲课,接着挂上听课记录吧
-
分块
这方面之前学过,不再从头讲述了,可以去看之前的分块笔记Link
-
势能分析
dottle刚讲过,就是一种分析复杂度的方法,分析完了就可以放心去写暴力了
搭配那几道分块食用
简单来说,就是把复杂度拆成两个部分,一个是原序列做完产生的复杂,一个是新加入玩意的复杂度
加起来即可
-
操作分块
这个trick有意思,先挂题:CF342E Xenia and Tree
可以发现,对于加点操作与询问操作,有两种最基础的做法,一种是直接跑遍历,查询复杂度 \(O(n)\) 修改复杂度 \(O(1)\)
第二种是预处理,加点后进行全图遍历,为每个结点赋答案值,修改复杂度 $ O(n) $ , 查询复杂度 $ O(1) $,有点根号分治的意思了
补充一下,树上任意两点的距离 \(dis_{u,v}\) 可以用公式:\(dis_{u,v}=deep_u+deep_v-2*deep_{LCA_{u,v}}\),查询复杂度是\(O(log_n)\)级
那么就可以每 $ \sqrt{n} $ 次操作后重构树上点答案值复杂为 \(O(n\sqrt{n})\),对根号操作内次的查询只让初值与根号前方的点比较复杂度\(O(n\sqrt{n} log_n)\)
总的复杂度就是\(O(nlog_n+n\sqrt{n}+n\sqrt{n}log_n)\),LCA预处理+做法1+做法2
-
根号分治,根号平衡
也是学过的玩意,挂个链接笔记吧Link
-
总结
感觉今天最重要的是复杂度的分析,当一道题的复杂度分析对了,再暴力的写法也会是是最正确的AC
2025/07/18
省流: 抄PPTing.
如常,楼下,stntn 后面忘了
-
博弈论入门&概念
简单来说,就是在两个人都不会犯错误的情况下,探索某一人是必输/必赢
-
简单&博弈
1 .Bash博弈
\(n\) 个石头,\(A,B\)轮流拿\(k \in[1.m]\) 个石头,拿到最后一块石头的是获胜者
solution:当n是m+1的倍数时,先手必败
2 .

考虑当集合不为空时先手必胜---把1拿了
3 .

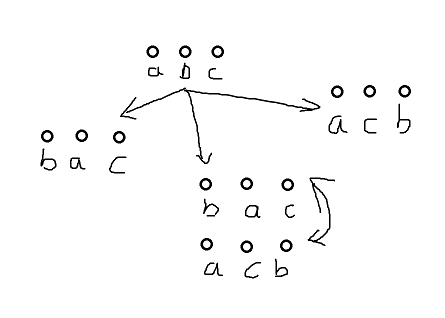
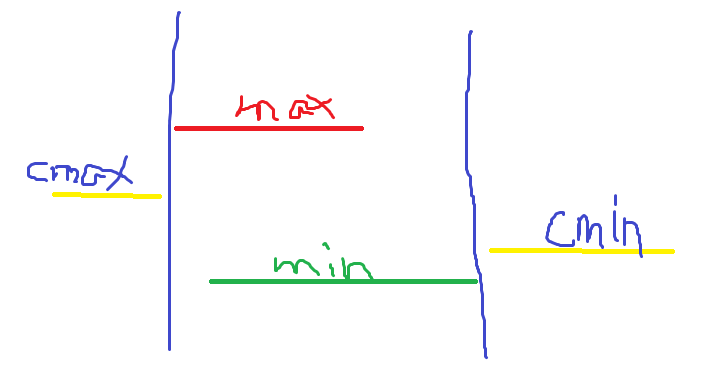
题面:CF1874A Jellyfish and Game
考虑只会一直交换全局amx与全局min,稍微约束判断即可
4 .

题面:CF1860C Game on Permutation
博弈论递推,求最长上升子序列
5 .

题面:CF1749C Number Game
模拟,随着i的变大,会有一些数自己出局,A一定选最大的,B一定尽早淘汰最小的
6. \(Nim\)游戏:异或和不为时先手必胜---自己百度去
-
博弈图和状态
将每个状态视为结点,连边建图,一般是\(DAG\)(有向无环图)
状态:必胜,必败....看名字就可以了
-
SG函数
笑,上次写这个忘了保存,不然我就直接挂链接了(
当当前结点\(u\)没有后继结点(必败状态),\(SG_u=0\)
否则\(SG_u=mex( \in_{Son_u}SG_v)\)
说人话就是所有儿子\(SG\)值组成的集合里取\(mex\)
\(mex\)指集合中没有出现的最小的非负整数
起点\(S\)的\(SG\)函数值\(SG_s\)就是这个游戏的\(SG函数值\)
组合游戏的\(SG\)函数值就是所有子游戏的\(SG\)函数值的异或和
P3185 [HNOI2007] 分裂游戏
后面忘了,写珂朵莉去了(
2025/07/19
今天考试,考试总结见:一点总结(
2025/07/20~2025/07/27
放一周的假
2025/07/27~2025/08/17
中山集训,内部消息,不透露
2025/08/21
今天是贪心专题,首先看了看dottle佬的ppt
所谓贪心其实就是证明最重要
- P8082 [COCI 2011/2012 #4] KEKS
从前往后去删除,保留剩余k位中最大的一个
贪心正确性显然 - P8898 [USACO22DEC] Feeding the Cows B
可以发现每头牛吃的屮离他越远越好,那么记录最右侧的屮位置,当需要更新的时候就从该点往后找最远的位置填,由于记录的最右位置只加不减,最多遍历\(O(n)\)次,可以通过该题,正确性显然 - P6243 [USACO06OPEN] The Milk Queue G
this
贪心式子可以用数学归纳法得出/证明 - P2255 [USACO14JAN] Recording the Moolympics S
考虑如果只有一个录音机时怎么做:
将所有活动结束时间排序,然后从初始结点开始能选就选
两个录音机怎么做?
将活动结束时间进行排序,然后遍历每个,用空闲的那个能选就选 - P2945 [USACO09MAR] Sand Castle S
考虑将a与b分别从高到低排序,然后直接每对算贡献 - P8896 「DPOI-1」道路规划
考虑拓扑,竞赛图的DAG,问题转换成在序列上把其变成在[L,R]之间的数 - CF525D Arthur and Walls
贪心染色,dfs一个∗点要被替换,当且仅当有一个包含它的2×2的矩阵中除它之外全是.点,向八个方向同时扩展 - CF3D Least Cost Bracket Sequence
先把字符串中的问号都换成右括号,如果左括号比右括号多,则在前面所有原来问号上找左右差值最小的换掉 - CF1208G Polygons
考虑什么时候加入 \(k\) 边形是最优的?
eg:如果我要加入6边形,那么我一定会先加入3边形,因为三边型的顶点全部被六边形覆盖着
可以推广:如果我要加入 \(k\) 边形,那么 \(k\) 边形前所有与\(k\)有公因数的 \(p\) 边形都会与 \(k\) 边形有相同的交点
所有每次添加 \(k\) 边形时会增加在 \(k\) 前面与 \(k\) 互质的数个数个新点
也就是\(\phi(k)\) !
然后就很显然了,欧拉函数是积性函数,当\(gcd(a,b)=1\) 时 \(\phi(a*b)=\phi(a)*\phi(b)\),直接用筛法将质数与欧拉数一起筛出即可
最后将 3~n 的所有欧拉排序,选 k 个最小的,加上初始三角形的2即为答案
2025/08/22
贪官模拟器,今天接着贪
- CF1085E Vasya and Templates
考虑分讨,但是我没大懂,先跳过吧 - P4765 [CERC2014] The Imp
看到物品数量为 \(10^5\) 但最多只会有 \(k<=10\) 个物品被变成灰,考虑dp
设 \(dp_{i,j}\) 表示买到前 \(i\) 个物品时用了 \(j\) 次魔法的最大收益,很容易推出转移方程:
\(dp_{i,0}=max(dp_{i-1,0} , a[i].val-a[i].cost)\) 先手表示选与不选
\(dp_{i,j}=max(dp_{i-1,j} , min(dp_{i-1,j-1}-a[i].cost,a[i].val-a[i].cost))\)
max表示我的最优状态,min表示恶魔干扰的最劣状态
转移顺序?价值从大到小!
考虑如果从小到大去选,即使不使用魔法你也无法最大化收益,所以直接从大到小去选! - CF1685C Bring Balance
考虑一个结论:任何括号数相同的括号序列在翻转两次以内一定会完成匹配
证明:
将左括号看成+1,右括号看成-1,就发现原先的括号序列变成了一条折线图,当折线上到x轴以下(小于零)才是不正确的
令\(a[i]\)为折线的前缀和数组,记录x为最大值,翻转 \([1,x],[x,n*2]\) 一定可以获得合法序列
考虑怎么只翻转一次:
令 l,r 是最前和最后一个前缀和小于 0 的位置,那么最终翻转的区间 \([L,R]\) 一定要满足 \(L≤l,R>r\) 贪心地选择 \(L≤l,R>r\) 且\(a_{L-1},a_R\)最大的 \([L,R]\) 检验即可 - CF436E Cardboard Box
记录 \(i\) 关拿一颗星的代价为 \(a_i\) , 拿两颗星的代价为 \(b_i\)
考虑如何从有 \(i\) 颗星星推到第 \(i+1\) 颗星星,有四种情况:
- 新选一个获取一颗星星的关 \(i\) ,代价为 \(a_i\)
- 将一个原来只有一颗星的关卡`\(i\) 变成两颗星 , 代价为 \(b_i-a_i\)
- 将一个原来只有一颗星的关卡 \(i\) 反悔一颗星 , 从新的关卡 \(j\) 拿两颗星 , 代价为 \(b_j-a_i\)
- 将一个原来有两颗星的关卡 \(i\) 反悔成只有一颗星 , 从新的关卡 \(j\) 拿两颗星 , 代价为 \((a_i-b_i)+b_j\)
那么我们维护五个优先队列,每次取队首更新即可
2025/08/23
今天上午考试,第二道题懂了,没切出来
- A. 剪切字符串 (lcp)
诈骗题,考虑答案上界,其实第一串选 \(n-2\),第二串选\(1\),第三串选\(1\)
\(lcp(a,b)+lcp(a,c)+lcp(b,c)\)最长也只能是\(3\)
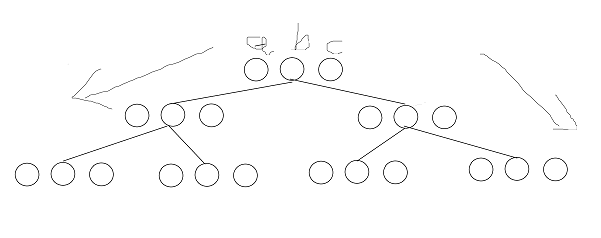
当第二串与第一串有一个不同,那么答案上界就变成\(1\)了,当第一串第二串第三串都有一个不同,答案上界就是0了,分讨即可 - B. 深度优先搜索树(dfs)
考虑什么时候可以有答案:当返祖边出现时,答案为\(2^k\),\(k\)是返祖边的数量 - C. 巡逻网络(net)
状压||随机化,还没调出来,因为最多只选四个点嘛 - D. 彩色括号(witch)
这个是真不会 - 杂题P4679[ZJOI2011] 道馆之战
恶心!调了3hours了,调不出来,整体上是树剖+线段树,不过要有维护信息有点多而已()
2025/08/24
晚上ABC,和明天混在一起总结
2025/08/25
贪贪贪,嘻嘻嘻
- P1650 田忌赛马
考虑跑两遍,第一遍统计可以获胜的最大值,第二遍找平局
将齐王和田忌的🐎按照从小到大排序,从小到大枚举田忌的🐎,从大到小枚举齐王的🐎,当田忌的🐎比齐王的🐎快,贪心选择 - P5749 [IOI 2019] 排列鞋子
考虑每次移动都是从右边最近的一个过来,那么开n给vector,存每种鞋子的位置,从右往左,树状数组跳过中间的鞋子 - P4823 [TJOI2013] 拯救小矮人
按照逃生高度排序,贪心dp - P6927 [ICPC 2016 WF] Swap Space
考虑分成两个数组,第一个存 \(a<=b\) 的 第二个存 \(a>b\) 的,分别按a从小到大,b从大到小排序,最后模拟即可
贪心正确性显然 - AT_agc023_f [AGC023F] 01 on Tree
考虑贪心,对于所有权值为0的点,当他的父节点全部拍下来了,那么把它马上拍下来就是最优的
所以可以考虑将子节点和父节点合并,考虑如何维护合并后结点的权值?
现在我有两个个结点a,b,那么当a放在前面时会产生\(a_{cnt1}*b_{cnt0}\)对逆序对,\(cnt_{1/0}\)表示该节点下方权值为\(1/0\)的结点个数,当b放在前面时会产生\(b_{cnt1}*a_{cnt0}\)对逆序对
所以当a比b更优时,即产生的逆序对最少,有\(a_{cnt1}*b_{cnt0}<a_{cnt0}*b_{cnt1}\),即以此优先队列排序即可
code: - 好消息,调出了道馆之战!
2025/08/26
最后的一天贪心了(
- P4409 [ZJOI2006] 皇帝的烦恼
每个勋章最多给\(n/2\)个将军,那么可以得出式子\(ans=\dfrac{\sum_{i=1}^{n}a_i}{\lfloor\frac{n}{2}\rfloor}\)
一共需要的勋章数/每种勋章最多可以给多少人 - P2123 皇后游戏
考虑怎么排律是最优的
![image]()
- AT_arc076_b [ABC065D] Built?
将x与y分别排序,给相邻两项分别连边,最后跑最小生成树即可,正确性显然
2025/08/27
晚上神秘CF,明天补吧
2025/08/28
进入了构造板块,首先观摩了 \(dottle\) 佬的ppt,知道了一个神秘构造称呼:人类智慧
- CF1512D Corrupted Array
考虑什么时候可以由a变成b
记录一个最大值maxx,一个次大值se_max
要么是a中所有数加起来等于se_max,maxx是随机数
要么其他数加起来等于maxx,用maxx-sum和等于的那个数是随机数,分讨即可 - AT_abc185_f [ABC185F] Range Xor Query
为什么在构造题单里???线段树裸题哇( - P5595 【XR-4】歌唱比赛
首先考虑什么时候无解:形如ZZZXY,就是Z只能出现在末尾一段连续段中
然后做完了,X:0 9 Y:9 0 Z: 1 1 - P3514 [POI 2011] LIZ-Lollipop
考虑一个结论:当X可以得到,那么X-2也可以得到
证明:
- 当x两端都为1时,同时删去两边,满足x-2
- 当x一端为二时,删去该端,满足x-2
那么很显然了,通过找到最大奇数与最大偶数,然后\(1e6\)的范围L,R桶处理即可
- P3640 [APIO2013] 出题人
造数据,不嘻嘻,考虑不同最短路算法的卡掉,分析算法结构
2025/08/29
构构造造
- AT_agc029_c [AGC029C] Lexicographic constraints
考虑二分答案,如何check?
模拟进位即可,注意从大到小的答案为一的特判即可 - AT_agc035_c [AGC035C] Skolem XOR Tree
分奇偶讨论,考虑两种路径
- x->x+1->1->x' (x%2==0)
- x->x-1->1->x' (x%2==1)
2025/08/30
考试,放假
2025/08/31
常规收假
2025/09/01
补了MZOJ的考试题与ABC的题,abc421f是唐题,链表思想,记录next数组即可
2025/09/02
考虑杂题,四道题一下午只做出来两道(
- P3423 [POI 2005] BAN-Bank Notes
完蛋了,先没有看出来背包,然后看出来了不会写,花了0.5h+重新学习01背包(
首先多重背包求最小方案,采用二进制优化(其实就是拆位)
然后考虑如何输出方案,可以发现,dp时记录一下选择,dfs就可以了 - P4563 [JXOI2018] 守卫
你被骗了,不要像我一样去搞斜率与凸包,\(O(n^3)\) 滚出(
考虑每个区间 \([L,R]\) 一定会在 \(R\) 位置放一个人,那么我们以 \(R\) 为基础(一定要选), \(O(n)\) 枚举 \(L\)
那么枚举的复杂度为 \(O(n^2)\) , 考虑区间dp合出答案
对于每个枚举的 \(R\) ,在枚举它的 \(L\) 时记录一个可以看到的最左边的端点 \(P\) 那么 \(P\) 之前的就一定是之前访问过的区间,
那么记区间 \([a,b]\) 的最小放人值为\(dp_{a,b}\) 则\(dp_{a,a}=1\)
\(dp_{L,R}=dp_{L,P}+1 , dp_{P,R}=1\)
最后异或上所有的 \(dp\) 值即为答案
2025/09/04
同上面02,四,二,懂?
考虑杂题,四道题一下午只做出来一道(
- P5504 [JSOI2011] 柠檬
斜率优化版子,李超树轮椅,嘻嘻嘻 - P3209 [HNOI2010] 平面图判定
考虑每一条边要么在曼哈顿回路形成的⚪内,要么在⚪外,2-Sat做完了,考虑平面图的欧拉公式: \(v+p-e=2\)
2025/09/05
考虑考试(炸
2025/09/06
考虑vp abc,abc422e 随机化有点意思,时间复杂度之王(
2025/09/09
考虑vp cf 1048 Div2
- CF2139A Maple and Multiplication
非常简单,考虑每次变化三种情况:
- a==b (0次)
- gcd(a,b)a||gcd(a,b)b (1次)
- gcd(a,b)==1 (2次)
- CF2139B Cake Collection
非常煎蛋,你考虑贪心去取,排序后按最后一秒从大到小分配求和即可 - CF2138A Cake Assignment
肥肠煎蛋,你观察到变换的次数不超过120次,且每次变换的上一步是固定的,所以你倒着去搜一遍即可 - CF2138B Antiamuny Wants to Learn Swap
你注意到值域范围很小,然后转化一下题意,你就是去求区间有没有逆序三元组,线段覆盖区间查最小值,三颗线段树维护最近前驱即可 - 不会了(
2025/09/12
考虑vp cf 1049 Div2
- CF2140A Shift Sort
考虑位移的实质:交换两个数,那么两个指针前后扫,贪心匹配即可 - CF2140B Another Divisibility Problem
注意到每次拼接的x都可以是原数的二倍,然后你把原数乘二。输出来就行了) - CF2140C Ultimate Value
不难发现,Bob总会在第二轮选择结束游戏(Alice可以一直还原Bob的行动,然后只会增加权值)
那么Alice肯定会在第一轮完成最优解
- +_min 换 -_max
- +_l 换 +_r
判断即可
- CF2140D A Cruel Segment's Thesis
访问 题解 谢谢喵)
2025/09/13
考虑上午核桃OJ考试下午四道杂题,下午忙于补做题记录只写了一道杂题(
- P3177 [HAOI2015] 树上染色
比较裸的树形dp,转移方程为
\(dp[u][j+p]= \max\limits_{v\in Son_u}^{j \le Siz_u p\le Siz_v}dp[u][j]+dp[v][p]+val*w\)
其中 dp[u][m] 表示以u为根的字树里选m个点染色对答案的贡献,从下往上dfs时处理合并,枚举j,p算贡献
其中w为连边的权值,val 为经过的次数 复杂度为\(O(n^2)\)
2025/09/16
考虑写CF2144喵
- CF2144A Cut the Array
n <100 直接枚举即可 - CF2144B Maximum Cost Permutation
贪心从前往后和从后往前找即可 - CF2144C Non-Descending Arrays
访问 题解 谢谢喵
2025/09/26
前面几天都在vp喵,补题不想记喵
- P2709 小B的询问
莫队版子喵,奇奇偶偶排排序序。 - P12621 [ICPC 2025 NAC] Circle of Leaf
考虑树形dp,\(dp_{u,0/1}\) 表示以 u 为根的子树中方案,从下往上推 - P4198 楼房重建
使用线段树维护一段最长上升的斜率, \(O( \log n)\) 来 \(push\) 下放
2025/10/03
考虑今天的考试)
- A. 大数定理(largenumber)
所有可能的两个数一定是相距 \((n-1)/2\) 才能只删这两个数达到序列为1的,单调栈模拟即可
2025/10/04
记一下今天vp的cf
- A. Increase or Smash
你发现n很小,于是可以while来砸碎序列中除零以外的最小值
当序列中全部为0,结束并输出 - B. Catching the Krug
考虑取横纵坐标的差的绝对值,因为B可以斜着走,所以A左右横跳是没有用的.
A只能往相反方向逃窜,加上A反与B距离判断max即可 - C. Triple Removal
由于只有0/1所以数量要么是三元组个数+1,要么是三元组的个数
前缀和判断是否有00或者11即可 - D. Division Versus Addition
访问题解谢谢喵) - P5278 算术天才⑨与等差数列
考虑形成等差序列的三个限制条件,设判断区间l,r是否可以形成公差为k的等差序列
- \([l,r].max-[l,r].min=(r-l)*k\)
- \([l,r]所有相邻差值的gcd=k\)
- \([l,r]没有相同的数\)
一二条维护区间最大最小值,区间差值gcd即可
2025/10/10
记一下今天的杂题)今天的题比较好
- P2964 [USACO09NOV] A Coin Game S
看到这题,第一眼就可以搜索dp定义
\(dp[i][j]\)表示取到第i个限制为j个时的最优解
\(dp[i][j]= \max_{x \in_{}[1,j]}(\sum_{a_i}-dp[i+x][x*2] )\)
就这样去搜,开\(O_2\)就可以A了,
但是你发现记搜的复杂度实际上有\(O(n^3)\)
所以正解不是直接搜
你发现其实dp[i][j]与dp[i][j-1]状态数只有两项差距,所以可以直接特判 - P1758 [NOI2009] 管道取珠
ddddpppp
考虑组合意义(
你发现一下:
我们要求 \(\sum a_i^2\)
我们独立地进行两次游戏,每次游戏都用相同的初始管道状态(相同的 s1 和 s2)
那么两场游戏都产生第i种序列的方案数?
第一次有\(a_i\)种方案产生序列\(i\)
第二次有\(a_i\)种方案产生序列\(i\)
两次都产生序列\(a_i\)的方案数就是\(a_i \times a_i=a_i^2\)
所以实际上跑一边计数dp即可
因为两个游戏完全对称,并且要求输出序列相同,实际上我们可以用一个四维 DP 来解:
定义 dp[i][j][x][y] 表示:
第一个游戏已取出了 i 个上管道球和 j 个下管道球(即剩余 n-i 上球, m-j 下球)
第二个游戏已取出了 x 个上管道球和 y 个下管道球(即剩余 n-x 上球, m-y 下球)
此时两个游戏已产生的输出序列完全相同(即之前取出的球颜色序列一样)
的方案数。
最终答案: dp[n][m][n][m](两个游戏都取完,输出序列相同)
然后你发现i+j=x+y只有取得球数量相等,序列才可能相同,所以可以优化掉一维
![image]()
然后你可以发现f[i][j][k]只与上一个状态有关,考虑作滚动即可
![image]()
- P2943 [USACO09MAR] Cleaning Up G
维护pre颜色段dp即可
2025/10/11
记一下今天的考试题)
- A. 瘟疫(plague)
你发现一下,n,m的范围只有两千,那么你bfs遍历一遍图,把连通块标上vis,记下大小
然后再扫一遍遍历四个编号,取min即可 - B. 颤骨图腾(beacon)
你发现你记录一下pre和net,然后每次就可以 \(n/k\) 遍历
然后对每个k记录一下,做完了?
$ \frac{1}{n}+\frac{2}{n}+\frac{3}{n}+\cdots+\frac{n-2}{n}+\frac{n-1}{n}+\frac{n}{n} $
时间很熟悉啊,你就是调和级数喵!
原式$ \approx n \log n $] - C. 死灵法师(wizard)
神秘东西,不会( - D. 亡灵骑士(rider)
你考虑背包+剪枝
首先直接作 \(o(r^2)\) 的背包一定是不行的你肯定要优化
还有剪枝,考虑什么时候卡的最慢:
![image]()
其中 \(x=sqrt(n)\)
2025/10/12
记一下昨天的abc
- C题
读了题,k<=10
状压一下,枚举做完了 - D题
k<=10
爆搜遍历一遍,然后记忆化一下,做完了 - E题
不会( - F题
折半搜索,直接枚举
考虑长度为n的不相邻序列只与长度为(n-1),(n-2)的不相邻序列有关,斐波拉契数列,其中\(fib_{30}\)大概是832040,然后记一下有没有选第一个,选作后一个,然后二分查一下,拼一拼就做完了)
2025/10/14
记一下今天的 cf1057 的vp
- CF2153A Circle of Apple Trees
签到题,派一遍序然后跑一遍就做完了 - CF2153B Bitwise Reversion
被骗了(
你考虑一下:
$ \because $
- $ a \And b = x$
- $ a \And c = y$
- $ b \And c = z$
$ \therefore $
好了,三个叠一起,判断一下是否相等即可(
- CF2153C Symmetrical Polygons
考虑首先一定要把成对的取完,然后成对的和加上一个数大于另一个数,二分判断即可 - CF2153D Not Alone
隔位dp,你发现要么两个相邻,要么三个相邻,因为所有数都可以被二和三完全分解,所以dp时只需要考虑前三位,关于断环成链,只需要右移三次dp判断即可
![image]()
2025/10/17
今天补了CF1058vp
记一下一道不错的图论:
- AT_joisc2016_j 危険なスケート
你考虑到相邻格子最多走两步,滑行到终点处只需要一步,建边跑最短路!
2025/10/18
敲了洛谷下午的SCP-S组模拟赛
2025/10/19
vp了abc428,记录一下
- A - Grandma's Footsteps
模拟即可 - B - Most Frequent Substrings
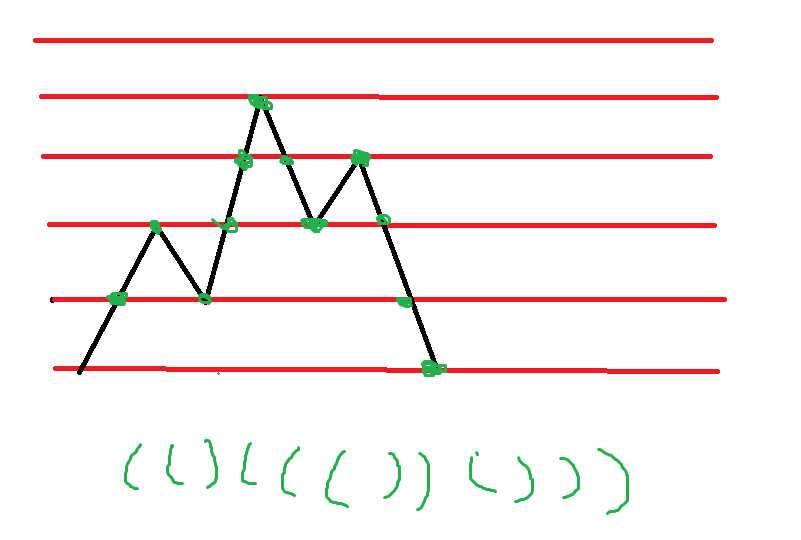
string 排序即可 - C - Brackets Stack Query
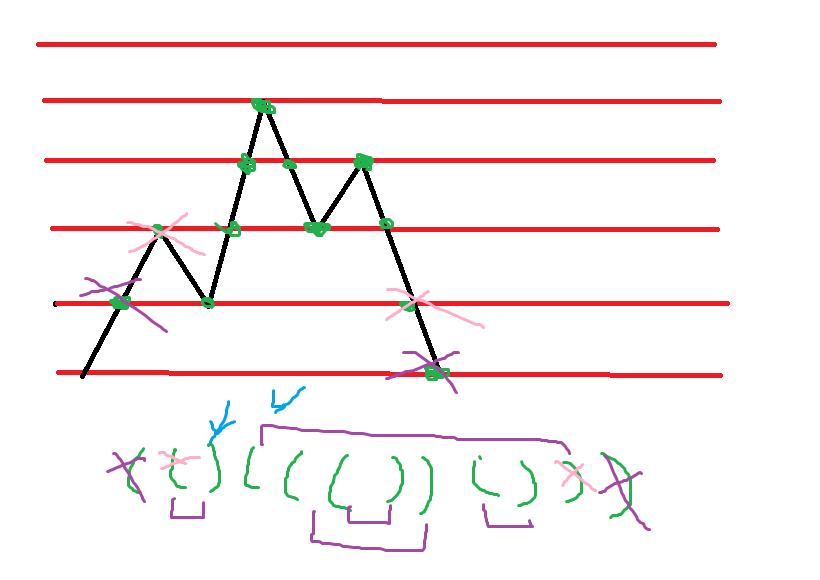
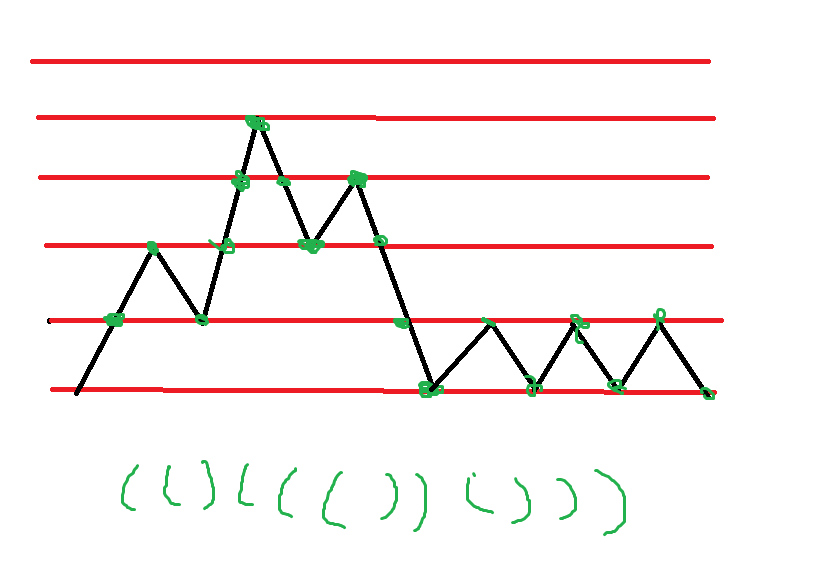
括号匹配,考虑维护折线,满足值为0且前方没有负数位置才可判断Yes - D - 183184
你发现你可以把新加x后组成的数表示为 \(c\times 10^i+x\)
用上界开根号减去下界即可,枚举这个 \(i\) 并且累加答案即可 - Farthest Vertex
发现所有取值只会在直径的两端之一,两遍 dfs 找到编号最大直径端点,搜出直径上的所有点并记录答案
再往下搜出答案处理即可
2025/10/20
vp了CF1060
完成了斜率优化的施工:Link
完成了对拍教程的施工:Link
2025/10/21
考了试,发现\(n^2\) 过了1e5,嘻嘻
完成了树上拓扑序计数的施工,在神秘题单里
2025/10/22
记一下今天的ARC208
-
A - Bitwise OR Game
首先你想到普通\(Nim\)游戏的结论:
\(Nim\)游戏中,状态($a_1,a_2,\cdots,a_n $)是必败状态当且仅当 \(a_{1} \oplus a_{2} \oplus \cdots \oplus a_{n}=0\)
你\(Nim\)游戏是最后一个取不到东西的人输
本题保证了区间或值相同,那么每一位都要留一个1
相当于先把每一位扣掉一个1再进行\(Nim\)游戏 -
B - Sum of Mod
考虑什么构造是最优的
\(a\to 2a-1\)
二分起点构造即可
2025/10/23
-
tree
你发现选的点与之前的无关,每个点选了后一定会产生儿子数量的连通块,所以直接背包即可 -
perm
考虑两个序列的转化:
你选一个数 x
把\(\le x\)的数全部赋成0,其他的赋成1
那么对于原来的序列,就会变成一个01串
我们用01串来探索两个串能不能转移得到
那么就会有结论:
转移后的串一定会在每个1都在转移前的串右边
因为每次是在交换逆序对,所以可以自己推一下,有了这个结论再来考虑dp
dp考虑状压,\(n\le 20\)所以可以直接记那些值用过了,从1~n枚举,每次把序列中新加入的数置成1,记现在的序列为s
那么在枚举当前的状态,s1的数量要与枚举的串1的数量相等(预处理局面对应的1的数量,\(o(1)\))
然后设枚举的串为t,\(s \to t\)要合法时,t就是合法串了,对于合法串,我们枚举其所有1的位置,走到该局面的方案数就是将枚举的1视为最后一个添加的局面的方案数,使用lowbit维护即可 -
P10641 BZOJ3252 攻略
首先你考虑将其转化成选k条不交的树链
树剖中对重儿子的定义是siz最大的,其实也可以维护到底部权职最大的
考虑树剖中有多少儿子就有多少链
那么对所有链取链顶,以向下最大权值为val,提出来排序选前k个即可 -
P3313 [SDOI2014] 旅行
你考虑树剖后开颜色数课线段树
动态开点,支删点操作即可 -
P4114 Qtree1
树剖版子 -
P3674 小清新人渣的本愿
首先离线莫队,这个非常显然
如何维护两个数的差为x?
其实就是问你区间\([l,r]\)中有没有 \(n\) 和 \(n+x\)
那么开一个 bitset s 为值域桶,将 bitset 向左移动 x 位,得到一个和原来偏移量 \(+x\) 的桶
将原先的桶和现在的桶与起来,若有重合,就会有 1,使用 any()函数 判断即可
如何维护两个数的和为x?
考虑区间 \([l,r]\) 中有没有一些东西
考虑记 \(x=m+n\) 那么有一个神奇的转化:
记大常数 \(C\) ,记录值域范围中 x 的 \(C-x\)
再维护一个 bitset t 维护 \(C-x\)
你发现 \((C-m)-(C-n)=n-m\)
将 t 右移 \(C-x\)位
那么 t 中的数就会变成 \(C-n-(C-x)\) = \(x-n\)
那么我们只需要在 s 中查询有没有 \(x-n\) 即可,因为 n 是一定有的,与起来判断
如何维护两个数的积为x?
直接 \(O(sqrt(x))\) 枚举x的因数,\(O(1)\)判断即可,时间复杂度为 \(O(m\times \sqrt{x})\)
2025/10/24
咦!1024程序员节!
- P10639 BZOJ4695 最佳女选手
吉司机线段树版子,考虑势能分析复杂度,发现记录了区间次小值与区间次大值,所以在懒标记下放时有延迟,是\(O(n \log ^2n)\)的东西 - AT_abc134_f [ABC134F] Permutation Oddness
非常神秘的dp题,你发现可以将其抽象其球和盒子配对
-![image]()
是一个非常像二分图匹配的东西
然后你对这个东西dp,每条连边的贡献是经过的黑线数量对这个诡异的东西做dp即可( - P7828 [CCO 2021] Swap Swap Sort
首先读懂题:给你一个排序权重和一个初始序列,每次交换相邻两个权重,问此时有多少逆序对
你发现每次只交换相邻两个数的权重,我们记两个数 \(x,y\) 的\(x\) 在 \(y\) 前面的数量为 \((x,y)\)
那么每次的交换可以看成的\(lastans+(x,y)-(y,x)\)
你发现 逆序对+顺序对=总对数 即记值 \(x\) 出现为\(cnt_x\)
$\therefore cnt_x \times cnt_y=(x,y)+(y,x) $
而记下出现次数是可以 \(O(1)\) 维护的
所以我们可以把式子转化:
- 所以瓶颈在于维护\((y,x)\)
发现值域很小所以考虑对数字\(x\)的出现次数\(cnt_x\)进行根号分治
我们设阈值为 \(S\)
当 \(cnt_x\) 小于 \(S\) 时我们记一个 \(vector\) 存 \(x\) 出现的每一个下标,两个都小于 \(S\) 时直接用双指针扫一遍 , 这么做是 \(O(q \times S)\) 的,因为出现次数不超过 \(S\) 嘛
当 \(cnt_x\) 大于 \(S\) 时,我们直接枚举后预处理出来对每种颜色的贡献,那么这种复杂度是 \(O(n\times \frac{n}{S})\)
这么做的总复杂度是\(O(q \times S+n\times \frac{n}{S})\)
问题在于 \(S\) 的取值, 均值不等式
\(\sqrt{a*b}\le \frac{a+b}{2}\) 当 \(a=b\) 时取等,即\(q\times S=n \times \frac{n}{S}\)
- 所以理论当\(S\)取100时取得最优复杂度,实测有波动
还有就是对最开始还要求一遍初始逆序对,我用的权值线段树)
- AT_abc295_h [ABC295Ex] E or m
记一下轮廓线dp的思想,轮廓线dp,也叫按位dp,指只记录一层有效状态,向下dp比如在种草问题中,不中相邻的草,那么我们就通过上一层的状态来之转移合法状态,不用枚举了
2025/10/25
记一道Ynoi
- P5048 [Ynoi2019 模拟赛] Yuno loves sqrt technology III
强制在线区间众数,考虑分块
记\(f[i][j]\)表示块 \(i\) 到块 \(j\) 的区间众数最大值
对于每个值用一个\(vector\)记下下标,暴力遍历散块,那么记一下这个位置在 vector 里的下标,l块就向右推 res 个,看下标是否在r的范围内,r块就左推 res 个,看下标是否在l的范围内,如果成立,res++即可
神秘三倍经验)
2025/10/26
记一下今天的 abc 429
d. 访问 题解谢谢喵
e. 多元bfs,搜索即可
- CF1422D Returning Home
你发现n很大,瞬移点很少,那么可以直接建边瞬移点,考虑最短路,很明显的是按照x,y排序,相邻两个点才建边,记得加上起点,在遍历一遍所以点到终点的曼哈顿距离+dis的最小值即可 - P5906 【模板】回滚莫队&不删除莫队
考虑回滚莫队的思想,你发现删除操作非常困难,因为你不好维护次大值,次次大值,次次次大值,那么我们就不要删除了,对于所以左端点在同一块内的询问分为一组,对于每一组询问,将右端点升序排列,那么每次莫队从左往右扫,只后不前,左端点每次暴力遍历,每跑到一个右端点就丢掉左端点,让左端点回归R[ql]+1,至于在同一块内的,直接暴力做!
2025/10/27
考試,跳過了
2025/10/28
vp了CF,不想记
2025/10/29
- A. 乘法(mul)
你发现这是一个很类似二进制加减法东西
那么有一个结论:
单个的一直接加上这一位,消耗为二
两个及以上的一可以通过二进制减法消耗为四
然后考虑只隔一个零的情况:
你发现要是隔了一个0也是二进制减法一起做,然后会有消耗二 - B. 环(circle)
你发现这是一个类似于分层图的东西,对于\(u_0\to v_1,u_1\to v_2,u_2\to v_0\)
然后只要可以从\(u_0\to u_1\)这个点即成立,写个tarjan判断强连通分量即可 - C. 栅栏(fence)
数据结构题,加上一点点贪心
首先先把最大高度序列维护出来
做一个类似滑动窗口的东西,区间查一下最小值,在开一颗线段树更新一下区间最大值
然后你会发现对于一段确定的最高的最大高度序列,相邻不一样的一定会让操作次数+1
而相邻相同的就是长度除x向上取整即可
2025/10/30
考虑记一下最近欠补的题
- P3472 [POI 2008] MAF-Mafia
首先,可以对毙人来建出一棵树,首先很明显,那些没人打的角色是肯定不会死的,所以他们打的人都是必死的,你发现在对于一条链,有必死的,有必活的,有不确定的
![image]()
- 于是拓扑跑一遍,最少就是隔一个杀一个,用这个可死可不死玩意数量/2.最大就是从后往前打,全杀了
但是还要考虑环状结构
![image]()
- 一样的,最小死一半,最大剩一个,注意判断自环即可
- P13984 数列分块入门 9
发现可以离线,显然可以回滚Mo队,只增不减,区间更新,记得离散化 - P1337 [JSOI2004] 平衡点 / 吊打XXX
Mo拟退火,对于每个点直接在其基础上加上随机值,概率替换答案,平衡态势能最小
完成了Mo拟退火的维修Link - AT_abc273_g [ABC273G] Row Column Sums 2
考虑dp求解。
\(dp_{i,j,k,l}\)表示还剩下 i 个 1 类行和 j 个 2 类行,来满足 k 个 1 类列和 l 个 2 类列的方案数。
然后你会发现\(i+2\times j=k+2\times l\)
枚举第一维,根据等式优化掉一维
![image]()
- AT_abc303_g [ABC303G] Bags Game
考虑区间dp \(d_{i,j}\) 表示区间[i,j]可以获得的最大收益,由于n是300,区间dp套ds优化找最小值即可 - AT_abc138_f [ABC138F] Coincidence
数位dp
考虑 :
$2x\le y $ , \(y \% x < y-x\)
$y<2x $ , \(y \% x=y-x\)
\(y-x\le y^x\)
那么只有 \(y<2x\) 才会有合法答案
又是 \(y>x\) 所以合法 x,y位数相同
当y二进制位为1,x可以是0可以是1
当y二进制位为0,x该位只能是0 - AT_abc225_f [ABC225F] String Cards
结论题,排序a+b<b+a后dp即可 - CF620F Xors on Segments
偷了,前缀和暴力 \(n^2\) 可以过嘻嘻 - CF442D Adam and Tree
记录f数组为节点子树最大颜色数
记录重,次重儿子,每次暴力向上更新至无法影响上层答案,类似树剖的复杂度,不超过\(\log\) - P5500 [LnOI2019] 真正的 OIer 从不女装
你发现再怎么翻转序列,也无法组成新的连续段,最多让首位接起来,所以其实只用维护每一块的左右颜色与最长颜色段即可
使用线段树维护,但是现在还没有调出来
2025/10/31
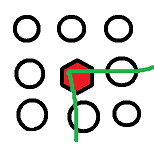
- P1852 跳跳棋
考虑两个状态之间的关系
首先对于一个状态的转移
![image]()
这是非常显然的,由于只能跳过一个棋子
所以说中间的那两个只会执行一个
你会发现只有左右会往外扩张,只有中间那个是收缩的
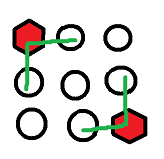
猜想一下,所有状态是会汇聚到一个点上的,也就是不能在收缩的,也就是会在\(b-a=c-b\)的时候收缩到极致
那么以这个点为根节点,可以拓展出一个类似于树结构的东西
![image]()
为什么两个点的收缩点是唯一确定的?
假设
\(x , x+a , x+a+a\) 可以扩展到 \(z+qc,z+tc,q+pc\)
\(y , y+b , y+b+b\) 也可以扩展到 \(z+qc,q+tc,q+pc\)
那么已知每次扩展后的坐标都是 \(m+qn\) 的形式出现,所以\(x=y=z,a=b=c\)
那么每个状态对应的收缩节点就是唯一的
那么先找到初始三元组的收缩三元组和目标三元组的收缩三元组,只有相同才可以YES
但是你发现值域是\(1e^9\)的
所以直接转移肯定是不行的,考虑如何加速转移
发现三个跳棋是没有区别的,那么每次跳跃可以看作\(a\to a+ab,b\to b+ab\)直接跳就可以了
所以具体来说,跳跃是\(O(\log_n)\)的
在把目标和当前的提到同一深度后二分找\(LCA\)即可
2025/11/01
下午是S组复赛,上午看了最短路的版子,并查集的版子,柯树模拟退火,结果只用上了并查集
- P14361 [CSP-S 2025] 社团招新 / club
首先你发现个社团最多有$ \frac{n}{2} $ 个人
那么比较显然的,每个人要么选最大值要么选次大值,不会考虑最小值
那么你考虑对于一个人,选他的最大值和次大值的差异在哪里
如果选了最大值,那么对于这个人就是最优的,如果选了次大值,相较于选最大值,亏了最大值减次大值的代价
那我们要和最大,就要亏的最少,考虑当一个玩意满了就每次把它代价最小的丢出去,把代价大的攥在手里
按照代价排序丢点即可 - P14362 [CSP-S 2025] 道路修复 / road(民间数据)
你先跑一遍最小生成树,把边的条数优化到,n
再对所有村庄作dfs式的状压最小生成树,是对的(
2025/11/02
开一下今天abc的 c,d,e
- C - Truck Driver
从后往前扫一遍,将后面第A个a的位置和第B个b的位置预处理出来
答案就是每个点的合法B位置减A位置的和 - D - Neighbor Distance
对这个东西开一个set,开map存最近的点位置,二分找到位置后比较大小更新,最后insert做完了 - E - Shift String
kmp版子,动态加一下就可以了
2025/11/03
- AT_arc149_d [ARC149D] Simultaneous Sugoroku
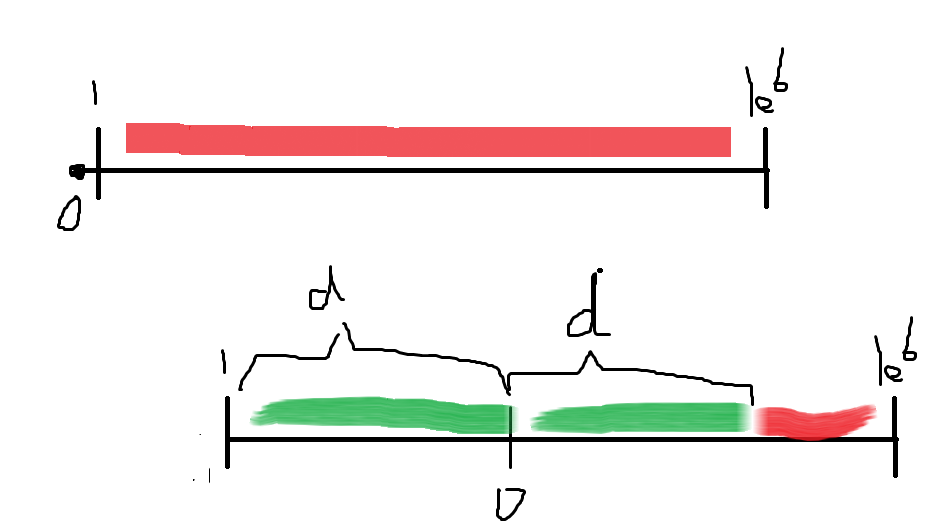
首先明确,我们移动的是原点,这样维护每个点的相对位置
然后对于第一次原点移动后,可以发现将\([1,1e^6]\)的区间分成了两个部分
![image]()
如图所示,绿色的区间可以作映射!
把小区间映射到大区间,YES时答案相等,NO时答案互为相反数
就这样映射后缩短左右区间大小查值答案时类似记搜一遍
只有最后作搜索,是线性的!
2025/11/04
- A. 矩阵matrix
可以发现,这是一个保证有解的东西
那么考虑它的解到底是什么样子的
类似于
\(\begin{align*} 01010\\ 00000 \\ 10101 \\ 00000 \\ 10101 \end{align*}\)
一定要隔一列,一行
还要考虑竖线的情况
就是把这个玩意翻转一下,做完了 - B. 介值intermediate
首先有一个结论:一段合法子序列最多只有四种颜色
把这个东西拍到序列上,用值域表示
![image]()
就是这个样子的
那么先考了\((km)^2\)枚举直接计数
会超时间,那么考虑对区间固定计数
![image]()
其实会有累加计数!
将前缀记下累加右移即可
还要考虑用两个值累计,以达到去重的效果
2025/11/05
两天没有写了,补一下题
-
#4241. Angle Beats 2.0
首先题意就很不好理解
已知一个网格图包含 $ * 和 . $
对于所有的 \(*\) ,将所有补成以 \(*\) 为直角点的直角三角形的方案数
比如样例是:
. . .
. * .
. . .
那么对应的四种补全就是
![image]()
![image]()
![image]()
![image]()
样例二对应的情况:
![image]()
考虑如何对方案数计数
你发现对于一个节点,你必须在上下,或者左右里面选一个
很像二分图,必须要选!
考虑对这个东西连边
那么对一个 * 点产生三条边
\(上 \to 下,左\to 右,自己\to 自己\)要是边界记得特判只能选上/下?左/右?自己连自己
所以考虑连通块,也就是先dfs维护联通分量,记录连通块的边数,点数
考虑分讨每个连通块的边点数量统计答案
当边数>点数,无解,输出0
当边数+1=点数,树形结构,答案累乘上点数
当边数=点数且没有自环,答案乘上而(环状结构,可以向左向右) -
#2570. Maximal Subsequence
先说题意,给一个序列,要求挑一个子序列使其LIS严格小于原序列的LIS
输出子序列的最大长度
比如样例
2 1 3->原序列最长为1 3,长度为2
答案子序列: 2 1 , LIS为1
4 6 5 2 1 3 ->LIS:4 6 长度为2
答案子序列: 4 5 2 1 LIS长度为1
首先考虑最native的作法:网络流!
对于每个点向继承上一个最大子序列连边
然后源点S向dp值为1的连边,汇点T向长度为dp值原序列LIS长度的点连边
考虑这样的图:
![image]()
你发现只要每次贪心把一条路径最左边删掉,直到没有通往终点的路径
做完了
2025/11/06
完成了邪恶倍增的blog,Link
明天补cdq分治)
2025/11/07
上午vp了cf
下午在建设cdqLink
2025/11/08
noip模拟赛
2025/11/09
- E - Reflection on Grid
首先这个东西如果翻两次肯定是不优的
所以保持原样,代价+0
变来变去,代价+1
对这个东西记搜搜一遍,做完了 - A - Bracket Game
首先你发现对于每个人操作的时候,如果已经是它想要的东西,就会马上结束游戏
所以1会把匹配正确的删一个,2会把不匹配的删正确
考虑括号的折线表达式
当这个玩意的折线有小于0的玩意出现的时候,此时就是不合法
我们知道,当一个完整的括号序被删掉一个,那么删一个把它变合法是唯一的
![image]()
那么考虑对着一边猛攻!
你发现first的目标就是把序列变成一个无论如何都修不好的序列
那么考虑让中间的一个玩意的折线降到0以下
![image]()
就是这样,但为什么之作一边?
![image]()
所以对着一边猛攻!
当出现()的玩意时,加速推进
当出现((,或者))时,删一个左边的,判断序列还是不是合法的
猛攻(n-k)/2次
维护一个区间最小值,然后对这个东西减去相对下降位置,这是对的
![image]()
2025/11/10
考试红温了,挂了160+
- #948. meirin
首先考虑20分,对于这个东西,直接\(n^4\)暴力去做,要开__int128
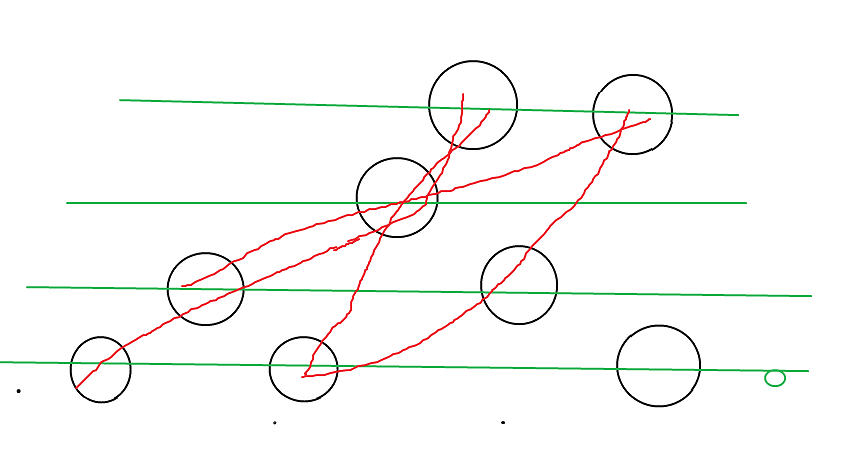
然后再考虑40分,作一个 \(O(nq)\) 的玩意
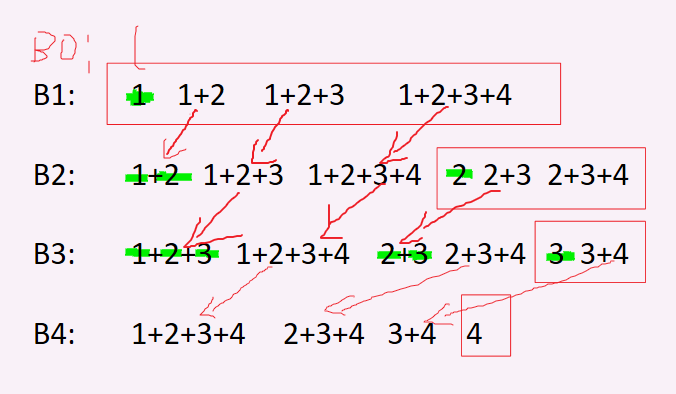
首先先把样子画一下
![image]()
发现可以把每个位置的贡献拆出来,从左往右算了再加起来
已知每段黑线的贡献是 a序列此段之和乘上b序列此段之和
那么拆一下式子
记 \(sa\) 为序列 \(a\) 的前缀和
\(sb\) 为序列 \(b\) 的前缀和
对于一个位置 i ,就会有它独特的贡献
比如说我有一个两项的序列,那么第一位有贡献
\(f_1=(sa_1-sa_0)\times (sb_1-sb_0)+(sa_2-sa_0)\times (sb_2-sb_0)\)
拆一下
\(f_1=(sa_1sb_1+sa_0sb_0-sa_0sb_1-a_1sb_0)+(sa_2sb_2+sa_0sb_0-sa_2sb_0-sa_0sb_2)\)
化简
\(f_1=(a_1b_1+a_2b_2)+(2\times sa_0sb_0)-(sa_0(sb_1+sb_2))-(sb_0(sa_1+sa_2))\)
可能看不出规律,那么再拆一个四位的
\(f_1=(sa_1-sa_0)(sb_1-sb_0)+ (sa_2-sa_0)(sb_2-sb_0)+(sa_2-sa_0)(sb_3-sb_0)+(sa_4-sa_0)(sb_4-sb_0)\)
化简
\(f_1=(a_1b_1+a_2b_2+a_3b_3+a_4b_4)+(4\times sa_0sb_0)-(sa_0(sb_1+sb_2+sb_3+sb_4))-(sb_0(sa_1+sa_2+sa_3+sa_4))\)
发现化简结果很有规律,第 \(i\) 项的贡献可以拆成 \(i\to n\)的\(sa,sb\)的积的和,加上 \((n-i+1)\) 项\(sa_{i-1}sb_{i-1}\) 的和,减去 \(sa_{i-1}\)乘上\(sb_i\to sb_n\)的和的积,减去 \(sb_{i-1}\)乘上\(sa_i\to sa_n\)的和的积
当序列长为三的时候,那么位置2带来的贡献就会是
\(f_2=(sa_2-sa_1)(sb_2-sb_1)+(sa_3-sa_1)(sb_3-sb_1)\)
化简可得
\(f_2=(sa_2sb_2+sa_3sb_3)+(2\times sa_1sb_1)-(sa_1(sb_2+sb_3))-(sb_1(sa_2+sa_3))\)
可得公式
\(f_i=(sa_i-sa_{i-1})\times(sb_i-sb_{i-1})+(sa_{i+1}-sa_{i-1})\times(sb_{i+1}-sb_{i-1})+\dots+(sa_n-sa_{i-1})\times(sb_n-sb_{i-1})\)
化简结果可以写成
\({\textstyle \sum_{i}^{n}sa_isb_i}+(n-i+1)(sa_{i-1}sb_{i-1})+sa_{i-1} {\textstyle \sum_{i}^{n}sb_i}+sb_{i-1} {\textstyle \sum_{i}^{n}sa_i}\)
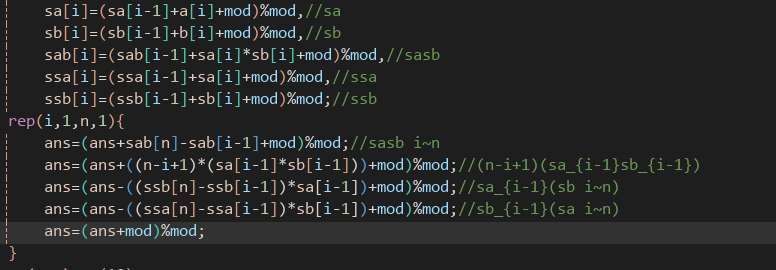
对于\({\textstyle \sum_{i}^{n}sa_isb_i}\)记录前缀和,再对\(sa,sb\)再记录前缀和,可以\(O(n)\)得出答案
代码长这样
![image]()
考虑正解
你发现你可以把每一位的贡献拆出来
那么对于一个a不变的序列,你能不能换一种拆分方式
让答案只与b有关,即处理出每一个 \(b_i\) 的参数
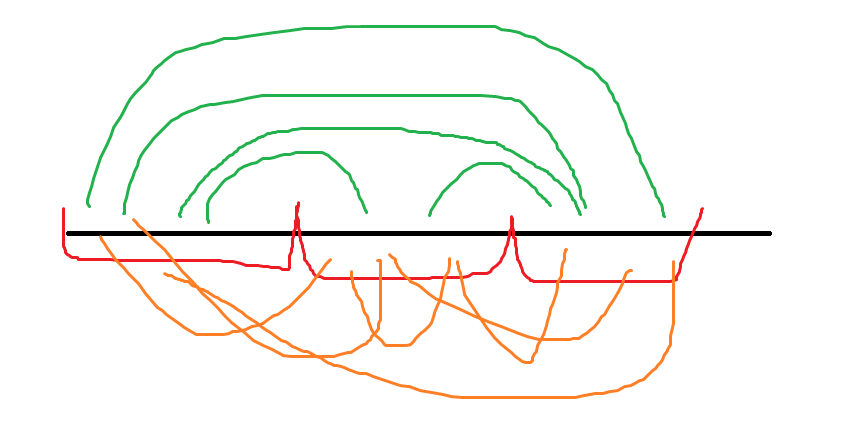
观察刚才的线线图
发现对于每一条线段
可以拆成两对相乘
比如一条 \(1\to 4\) 的线段
它的贡献其实是\(f=(b_1+b_2+b_3+b_4)(a_1+a_2+a_3+a_4)\)
可以变成
\(f=b_1(a_1+a_2+a_3+a4)+b_2(a_1+a_2+a_3+a_4)+b_3(a_1+a_2+a_3+a_4)+b_4(a_1+a_2+a_3+a_4)\)
一条 \(2\to 5\) 的线段
可以变成
\(f=b_2(a_2+a_3+a_4+a5)+b_3(a_2+a_3+a_4+a5)+b_4(a_2+a_3+a_4+a5)+b_5(a_2+a_3+a_4+a5)\)
把每个\(b_i\)要乘的数加起来再求和也是对的!
也就是说,我们把开始的式子
\(\sum_{l=1}^{n} \sum_{r=l}^{n}\left(\sum_{i=l}^{r} a_{i}\right) \times\left(\sum_{i=l}^{r} b_{i}\right) \bmod 1000000007\)
设成了一个
\(\sum_{i=1}^{n}b_i\times f_i\)
其中\(f_i\)是\(b_i\)对应的很多a值的和
现在的问题在于求解\(f_i\)
我们把一个长为4的序列每个\(b_i\)对应的a值和列出来省略的a字符
![image]()
发现每次到下一项会加一些,减一些
![image]()
框起来的是每次加的,绿🖊涂掉的是删去的
发现每次加上的是上一次加上的减去最前面的一类数
每次减去的是上一次减去的加上i个a[i]
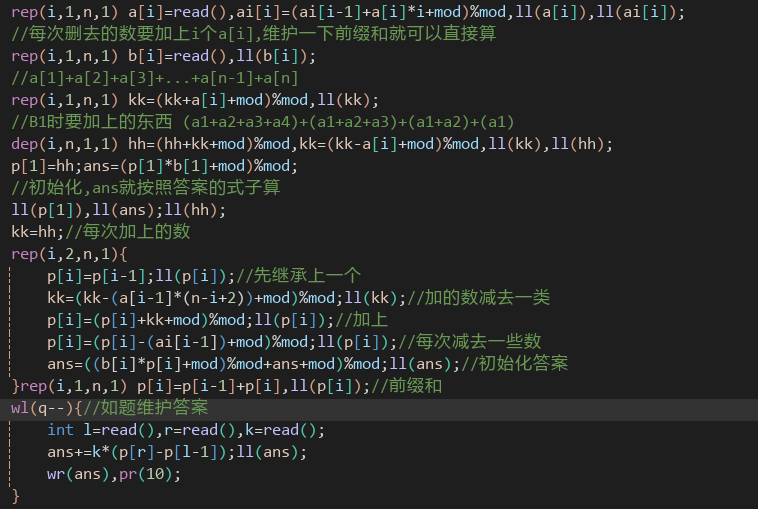
那么直接维护这个东西
你会发现转换的东西就会变成一段前缀和,做完了
![image]()
2025/11/11
考试4道,只会一道(
剩下的题解都看不弄明白
- A. 法国
首先你发现,每个数最多修改\(\sqrt{V}\)次
又有\(n,m,v\)同阶
所以考虑直接维护下一个让它变小的数的大小
查询的时候顺便修改
发现区间信息可以合并,lazy的tag很方便,查询的时候如果小于tag,直接返回处理好的值即可
所以这么作是 \(O(m \times\log n \times\sqrt{V})\) 的
\(m,n,V\) 同阶
所以复杂度是\(O(n\sqrt{n}\log{n})\)的
无法通过\(3e^5\) 但是卡卡就A了
2025/11/12
- P8541 「Wdoi-2」死亡之后愈发愉悦
你首先打表找个规律
11011100111100011111000011111100000111111100000011111111
\(n\) 个 1 后跟 \(n-1\) 个 0
这是可以证明的
设 \(m^2 \le x\le(m+1)^2\)
那么一个可爱的数x要满足
\(m^2\le x<\frac{m^2+(m+1)^2}{2}\)
后面是几何平均数,所以在\(x^2,(x+1)^2\)中1,0是对半开的,又是因为左边平方可以取等,所以1会多一个
再考虑具体解法
对于 \(10^{12}\) 规模的数据,还只能问64次,那么倍增就会非常明显了。
考虑倍增的做法。
先问a自己是什么,再每次扩大步数,找下一个与自己不同的节点,这就是你的下一块。
考虑正确性证明,对于每个连续段,下一个不一样的连续段的大小一定是大于等于该段的,所以一定不会跳出去。
找到下一个位置后再倍增处理下一块的大小,逆推a即可
2025/11/13
今天考试A了一个估分20的暴力T3?????
神秘数据,kkk
2025/11/14
a呀,今天太神秘了,我在高一完成了P3803 模板FFT,你也快来试试叭
考前随机说话,哈哈哈噫噫噫咕咕咕嘎嘎嘎MoMoMoMoMoMoMo丸是灵珠
- AT_abc220_h [ABC220H] Security Camera
首先知道,正难则反,与其直接统计覆盖m条的答案,不如统计两边都没有放监控的方案
在模2意义下的异或和可以直观获得答案的奇偶性
那么考虑对这个东西作折半搜索,对于每一半统计左右连边的贡献,而左右的奇偶性用\(2^2\)枚举
然后要用什么神秘的fwt或者高维前缀和,现在不会qmq - AT_agc036_d [AGC036D] Negative Cycle
最后答案一定是这样的图,考虑dp
![image]()
表面上是\(n^4\)其实第一维只会是1,2,是\(n^3\)的 - AT_agc056_b [AGC056B] Range Argmax
考虑对x计数,每次对应的p都取字典序最大的
优化成区间dp
2025/11/15
洛谷的NOIP模拟,A了T1,T2看题解会了,不想计(
2025/11/16
- A - Always Increasing
首先考虑想要最小末尾态的样子:
由于严格上升,所以所有可能的点一定会向等差序列变换,所以理想最优
状态一定是形如 1 2 3 4 5 .... n-2 n-1 n
这样的
但是修改操作可以强行提升一个点的权值,所以考虑将修改之后的不下降序列都加上提升的权值
还有就是加上也没有先前的大的时候不能再加
很明显了,维护一个数据结构,支持后缀加,单点查
最后答案是所有点的权值总和,减去新加的权值和 - B - Remove Median Operations
首先我们模拟删去中位数的过程
![image]()
加入蓝色的点
![image]()
![image]()
![image]()
所以最后得到的是a,b可重序列的前n/2个和后n/2个
数据结构维护即可,STL,平衡树,动态开点线段树``````
2025/11/17
- A. Alice and Bob
🍳题,记一下多少数比a大,多少数比a小后取max+1,-1即可 - B. Drifting Away
🍳题,直接读进来后模拟即可 - C. Range Operation
🍳题,推一个式子后记录max即可 - D1. Removal of a Sequence (Easy Version)
🍳题,直接二分,x很小,直接作即可 - D2. Removal of a Sequence (Hard Version)
🍳题,考虑每次前进的实际推进步数,>1e12后break,ans=-1; - E. Points Selection
🍳题,状压?好吧不会( - P5355 [Ynoi Easy Round 2017] 由乃的玉米田
![image]()
对于除法根号分治,大于\(\sqrt{n}\)的直接暴力枚举
对于小于的预处理最近答案,然后每次查区间最大值是否大于l
2025/11/18
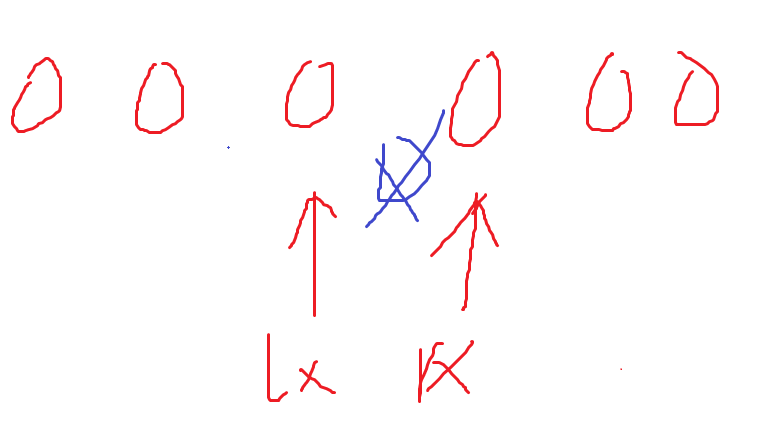
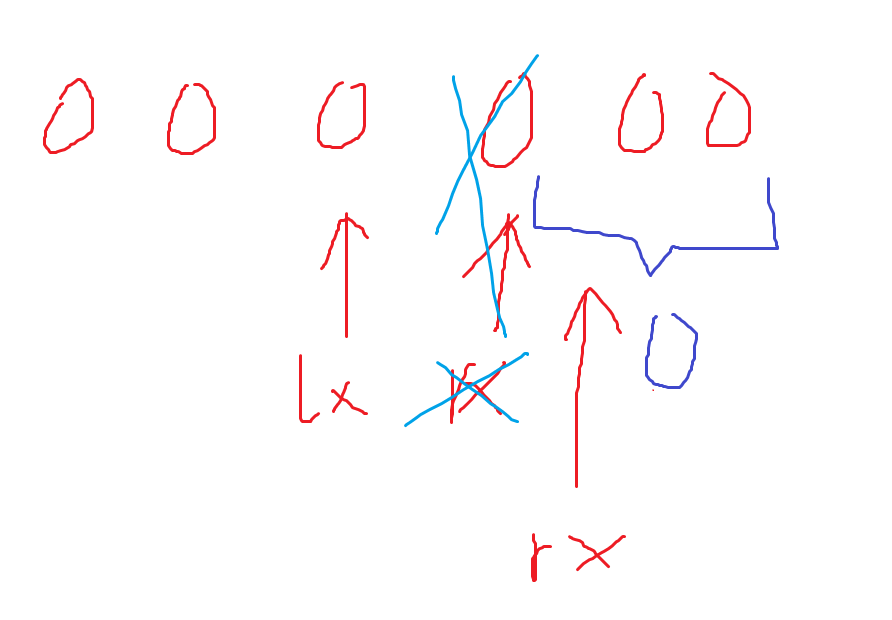
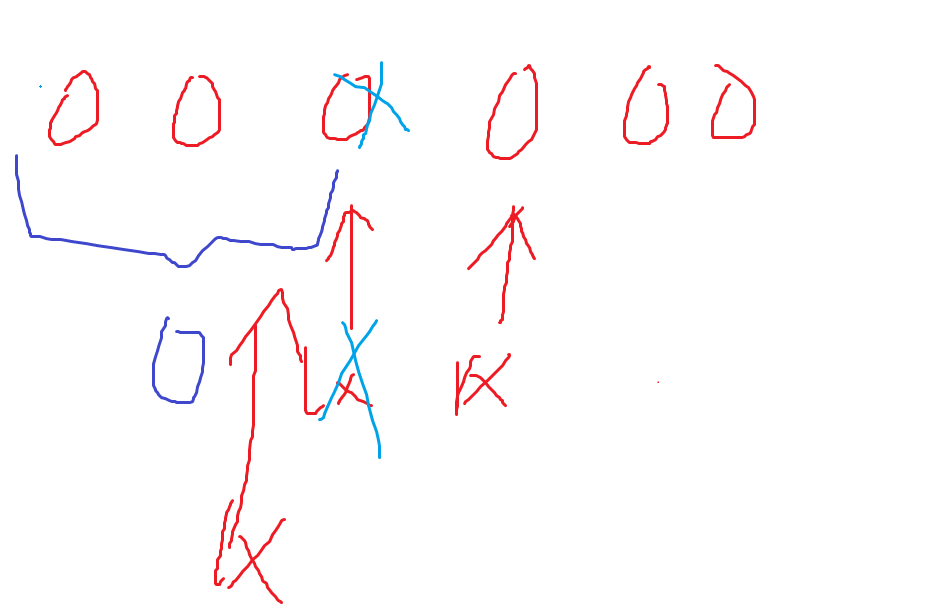
- B. boss
先看一段神秘思路
![image]()
哈哈,考场前后手搓了20kb的代码,嘻嘻嘻
好了,思路里说了
对于每一段新的安全的位置,里面的不管它,端点由自己与左右不安全的点走过来取min即可
考场上没有调出来(
2025/11/21
好多天没有计记录了啊,为什么呢,感觉这几天不对劲,没有斗志了,模拟赛连续好几次挂大分,有点浑噩
不能再这样下去了!先写写这几天写了写啥吧
-
AT_abc293_h [ABC293Ex] Optimal Path Decomposition
考虑一个判定思路,如果给出一个数量限制k,能否在dfs一遍的情况下判断是否可以染成
定义\(f_{i,{0,1,2}}\) 表示对于结点i有\({0,1,2}\)个相同颜色的结点的子树中颜色最少需要多少个
然后用1的儿子和2的儿子+1转移自己,只转移在k范围内的f值即可\(O(n)\)判断
那么一个很显然的结论,对于一个树,用5种颜色可以染,那么用六种颜色也可以染
所以二分答案做判断即可 -
P4359 [CQOI2016] 伪光滑数
暴力做法,对于128以内的质数直接存出来,对于每个点动态调整大小即可
还有一场cf和两场考试,不想记了,我想说加油吧,noip不远了,就当是为了那个!
2025/11/24
咕了好久,这几天晚上有事/kel
- A. 魔力屏障
这辈子想不到的区间dp
你家出题说\(n^3v^2\)可作?关键是你的\(x\le 70,v\le 150\)
算了,只要知道是区间dp就可以了,式子很好转移的 - C. 博弈
好题,考场上估分100,出分是0,但是很服气
考虑到每次博弈其实是可以在老鼠钻进死胡同后封死四周,迫使老鼠只能由一条路通向终点,对这个二分答案
做一个dp转移 - A. 基于1的算术
简单题,考虑到对于这个跑爆搜+贪心,对于一个数,要么是多正位一减去一个数,要么少正位1加上一个数
要么为进位1减去一个数,要么为退位1加上一个数,模拟记忆化即可 - B. 逃离
神秘题,考虑对于每一辆车的可以贪心的考虑开到终点其实是尾巴长度加上路程除以速度
所以每次个用时最多的那个人加速,再把它塞回堆里即可
![image]()
![image]()
![image]()
踩标了嘻嘻嘻
5. C. 南斯拉夫
建图后判断奇偶性即可
6. D. 数数
神秘构造(
考虑对式子的两边同时乘上\((a_i+a_j+1)\)最后\((a_i),(a_j)\)会分离.
2025/11/26
-
AT_arc157_e [ARC157E] XXYX Binary Tree
首先,由于限制了YY这样的玩意,所以父親和兒子不能兩個都是Y,很像一個二分圖染色的狀物
發現其實通過B,C的限制,Y的數量其實是固定的,如果非根節點,那麽非葉子可以提供1個XY,兩個YX
如果是葉子節點,可以提供兩個XY,而體面給了兒子數量的限定
所以考慮大力dp,定義 \(f_{i,j,0/1}\) 表示以i為跟的子樹中,有j個葉子是Y,自己是否是Y,可以獲得的最大非葉子節點為Y的數量,可以東條調整,所以直接樹上背包轉移,對于根節點做一個特判即可 -
A. 矩形(rect)
666考場第一名,下筆如sb
![image]()
哈哈哈,allin最後沒有拿到分
好了,説回正軌
对于每个矩形,考虑其每次覆盖的交集被覆盖过多少次
首先如果一片区域被覆盖了\(x\)次
那么在选\(k\)片区域相交时,就会有
\(C^{k}_{n}\)个选取的区间,会有\(C^{n-x}_{k}\) 次选不到
即计恰好被覆盖次数为\(x\) 的区间大小为\(cnt_x\),选取\(k\)个区间时
\(ans[k]=\sum_{i=1}^{n}\times (C^{k}_{n}-C^{k}_{n-k})\)
值域过大时二维离散前缀和即可 -
B. 排列(permutation)
首先考虑一端区间的贡献由来
可以发现,如果我们要排序一个区间,那么一定会是不会选取相交的,比如我们会选择[1,5]而不会选择[1,3]+[2,5]
所以划分区间之后,可以将一段\(f_{l,r}\)计算表示
首先给出式子;
\(f_{l,r}=(r-l+1)-k_{l,r}\),其中\(k_{l,r}\)表示区间\([l,r]\)最多可以划分出多少段
为什么是这个式子?
首先如果一整段都要排序,那么代价为\(r-l+1-1\)如果可以在中间分开,那么代价为\(mid-l+r-(mid+1)=r-l-1=r-l+1-2\)
如果一整段都是有序的,那么排序的代价为\(r-l+1-(r-l+1)=0\)所以我们要最小化代价,就要最大化划分段数
想要最大化划分段数,首先要明晰划分段如何是合法的
如果在这个位置划分,那么这个位置前面的数都要小于后面的数,很像cdq三维计算跨区间贡献的思考
所以对原来的式子转化一下
\(ans=\sum^{n}_{l=1}\sum^{n}_{r=l}f_{i,j}=\sum^{n}_{l=1}\sum^{n}_{r=l}(r-l+1)-k_{l,r}=\sum^{n}_{l=1}\sum^{n}_{r=l}(r-l+1)-\sum^{n}_{l=1}\sum^{n}_{r=l}k_{l,r}\)
这样就拆成了两个部分
先考虑前半部分的贡献
\(\sum^{n}_{l=1}\sum^{n}_{r=l}(r-l+1)=\sum^{n}_{l=1}\sum^{n}_{r=l}r-\sum^{n}_{l=1}\sum^{n}_{r=l}l+\sum^{n}_{l=1}\sum^{n}_{r=l}=\sum^{n}_{l=1}\frac{(n-l+1)(n+l)}{2}-\sum^{n}_{l=1}(n-l+1)*l+\frac{n(n+1)}{2}\)
这个玩意维护是非常方便的,可以直接预处理,所以现在只考虑第二项



 一点记录罢了(
一点记录罢了(












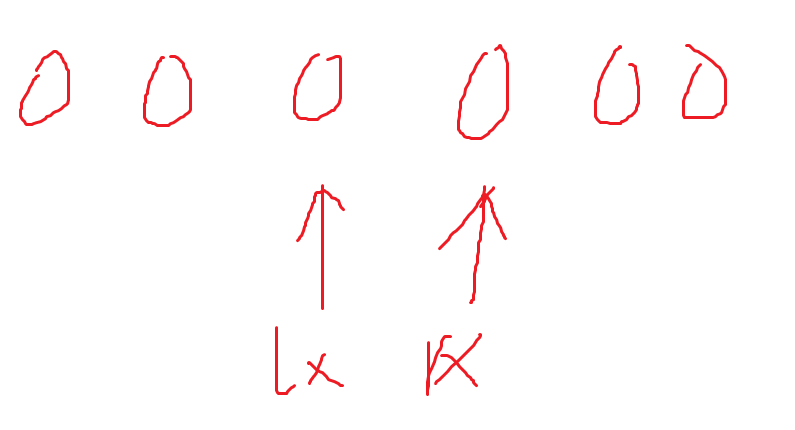






 浙公网安备 33010602011771号
浙公网安备 33010602011771号