模拟退火吙🔥

爬山算法

每次贪心向最优的一个点替换答案。


优点在于贪心，缺点也在于贪心，可能只到局部最优解，不能找到全局最优解。

模拟退火

退火是热力学的术语，该算法运用了模拟退火的思想，我们进行随机化枚举，每次更新答案后缩小边界，再随机化枚举，只到设置的温度降为0。

解决的问题类型 np问题

直接找正解无法做到多项式时间

1. 旅行商问题(TSP)
2. 费马点
3. ...

一个比喻

主要步骤

1. 设置初始温度 \(T\).
2. 修改答案,找到一个新的状态.
3. 计算差值 \(\Delta E\)
4. 选择最优解.
5. 如果没有先前答案优,也以平衡概率随机替换答案.\(exp=(\Delta E/T)\)
6. 每一次结束操作后将 \(T\) 乘上一个系数.(一遍取 0.985 ~ 0.999)

例图

随着温度的降低，跳跃越来越不随机，最优解也越来越稳定

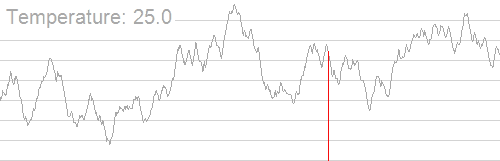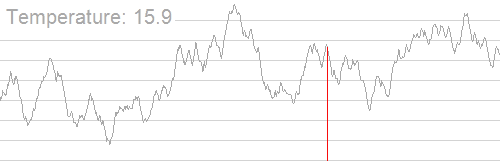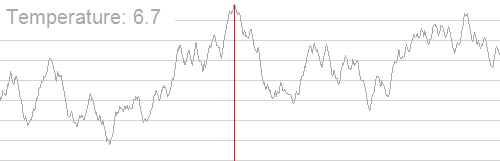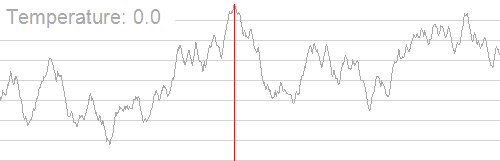
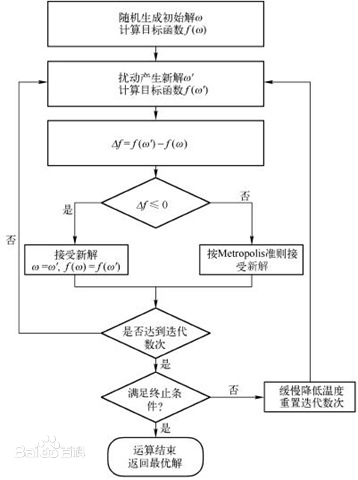
伪代码

eps=1e-15;T=初温;
while(T>eps){
	now=更新状态.
	E=calc(now)-calc(ans);
	if(E优) ans=now;
	else if(平衡概率) ans=now;
	T*=降温系数;
}

例题

P1337 [JSOI2004] 平衡点 / 吊打XXX
其实就是求 \(n\) 个点的类带权费马点.

int n,x[1005],y[1005],w[1005];
inline lb angry(lb X,lb Y){//对应的势能
	lb res=0;
	rep(i,1,n,1)
		res=res+std::sqrt(((X-x[i])*(X-x[i]))+((Y-y[i])*(Y-y[i])))*w[i];
	return res;
}
lb eps=1e-15,T=10086,ax,ay,ans;
inline void solve(){
	lb t=T;//初温
	while(t>eps){//边界
		lb X=ax+(rand()*2-RAND_MAX)*t,
		   Y=ay+(rand()*2-RAND_MAX)*t;
		lb now=angry(X,Y),E=now-ans;
		if(E<0){//更新
			ax=X,ay=Y,ans=now;
		}else if(exp(-E/t)*RAND_MAX>rand()) ax=X,ay=Y,ans=now;
		t=t*0.998;
	}
}
signed main(){
	n=read();
	rep(i,1,n,1) 
		x[i]=read(),y[i]=read(),w[i]=read(),
		ax+=x[i],ay+=y[i];
	ax=(lb)ax/n;ay=(lb)ay/n;ans=angry(ax,ay);
	int chr=4;
	wl(chr--) solve();
	printf("%.3Lf %.3Lf",ax,ay);
	return 0;
}

习题

1. P4044 [AHOI2014/JSOI2014] 保龄球
   非常裸的版子,考虑直接交换两个位置,记得判断合法

int n,m,a[55],b[55],Ans;
inline int g(){
	int res=0,ll=INF;
	rep(i,1,n,1){
		if(ll==INF){
			res+=a[i]+b[i];
			if(a[i]==10)
				ll=1;
			else if(a[i]+b[i]==10) ll=2;
		}else{
			int x=a[i]+b[i];
			res+=x;
			if(ll==1) res+=x;
			if(ll==2) res+=a[i];
			ll=0;
			if(a[i]==10) ll=1;
			else if(a[i]+b[i]==10) ll=2;
		}
	}
	if(a[n]==10) res+=(a[n+1]+b[n+1])*2;
	Ans=max(Ans,res);
	return res;
}
lb eps=1e-15,T=100088;
inline void solve(){
	lb t=T;
	while(t>eps){
		int ans=g(),A=rand()%m+1,B=rand()%m+1,now,E;
		while(A==B) A=rand()%m+1,B=rand()%m+1;
		std::swap(a[A],a[B]);
		std::swap(b[A],b[B]);
		if((n+(a[n]==10))==m){
			now=g();E=now-ans;
			if(E<0&&(exp(E/t)<(lb)rand()/RAND_MAX))
				std::swap(a[A],a[B]),std::swap(b[A],b[B]);
		}else std::swap(a[A],a[B]),std::swap(b[A],b[B]);
		t=t*0.998;
	}
}
signed main(){
	n=m=read();rep(i,1,n,1) a[i]=read(),b[i]=read();
	if(a[n]==10) m=n+1,a[m]=read(),b[m]=read();
	rep(i,1,10,1)  solve();
	wr(Ans),pr(10);
	return 0;
}

2. P2503 [HAOI2006] 均分数据
   直接枚举那个数字放在那个区域中

int n,m,a[25],he[10],pos[25];
lb ans=INF;
inline lb g(){
	lb x_=0;
	rep(i,1,m,1) x_+=he[i];
	x_=x_/m;
	lb res=0;
	rep(i,1,m,1) res+=(x_-he[i])*(x_-he[i]);
	res=res/m;
	return sqrt(res);
}
inline void solve(){
	lb t=10000,eps=1e-15;
	rep(i,1,n,1){
		pos[i]=Rand()%m+1;
		he[pos[i]]+=a[i];
	}
	lb cur=g();
	while(t>eps){
		int pl=Rand()%n+1;
		int old=pos[pl];
		int new_=Rand()%m+1;
		while(new_==old) new_=Rand()%m+1;
		he[old]-=a[pl];
		he[new_]+=a[pl];
		pos[pl]=new_;
		lb now=g();
		lb E=now-cur;
		if(E<0||exp(-E/t)*RAND_MAX>rand()){
			cur=now;
		}else{
			he[new_]-=a[pl];
			he[old]+=a[pl];
			pos[pl]=old;
		}
		t*=0.999;
	}
	ans=min(ans,cur);
}

signed main(){
	srand(time(0));
	n=read(),m=read();
	rep(i,1,n,1) a[i]=read();
	rep(i,1,75,1){
		me(he,0);me(pos,0);
		solve();
	}
	printf("%.2Lf",ans);
	return 0;
}

3. P3878 [TJOI2010] 分金币
   和2很像，只不过是分成两组
4. P4360 [CEOI 2004] 锯木厂选址
   推一下式子，O（1）得出锯木厂修在这两个地方的答案

int n,ans=INF,w[M],d[M],wd;
inline int g(int a,int b){
	int res=0;
	if(a>b) swap(a,b);
	res=(d[a]*w[a])+(d[b]*(w[b]-w[a]))+(d[n+1]*(w[n]-w[b]));
	res=res-wd;
	return res;
}
int a,b;
inline void solve(){
	lb t=2001,eps=1e-15;
	while(t>eps){
		int aa=round((2.0*rand()/RAND_MAX-1)*t);
		int bb=round((2.0*rand()/RAND_MAX-1)*t);
		aa=((a+aa)%n+n)%n;
		bb=((b+bb)%n+n)%n;
		int now=g(aa,bb),E=ans-now;
		if(E>0) a=aa,b=bb,ans=now;
		else if(exp(E/t)*RAND_MAX>rand()) a=aa,b=bb,ans=now;
		t=t*0.999;
	}
}
signed main(){
	n=read();
	if(n==2) return wr(0),0;
	
	rep(i,1,n,1){
		int W=read(),D=read();
		w[i]=w[i-1]+W;d[i+1]=d[i]+D;
		wd=wd+d[i]*W;
	}
	int chr=10;
	wl(chr--) solve();
	if(n==4&&ans!=1050) return wr(9),0;
	wr(ans),pr(10);
	return 0;
}