cdq分治 学习哔叽
写在前面
分治,非常基础的思想,分一为多,合多为一,用途广泛而自然。
以下是正文:
提单Link
基础思想:
考虑一段序列划分成两半统计答案。

比如要统计区间贡献,那么将原区间的贡献拆成三个部分。

绿的,蓝的,紫的
完全在左半边的,完全在右半边的。
横跨左右两边的。
递归处理左右区间)
处理的方向:
- 偏序问题(一维?二维!三维!四维)
- 优化dp
偏序问题
版子P3810 【模板】三维偏序(陌上花开)
就是每个元素有 \(a,b,c\) 三个属性
问满足 $i_a\le j_a,i_b\le j_b,i_c\le j_c $
这三个条件的点对 \((i,j)\) 的个数.
对于第一维偏序,可以直接 \(n \log n\)排序
这样前面的a值一定比后面的a值要小,解决一维.
考虑掏二三维
首先你得知道离线二维偏序的做法.
P10814 【模板】离线二维数点
其实就是问你区间的二维数点

这个会用到树状数组的状物,考虑延续二维数点的思想,摁死一维,求另一维
挂一下代码
/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(ch,cr) for(auto ch:cr)
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
#define wl while
#define max(a,b)((a)>(b)?(a):(b))
#define min(a,b)((a)<(b)?(a):(b))
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=5e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
struct Node{
int a,b,c;
int res=0,num=0;
inline bool operator *(const Node x)const{
return ((a==x.a)&&(b==x.b)&&(c==x.c));
}
}a[M],b[M];
inline bool c1(Node x,Node y){return x.a==y.a?x.b==y.b?x.c<y.c:x.b<y.b:x.a<y.a;}
inline bool c2(Node x,Node y){return x.b==y.b?x.c<y.c:x.b<y.b;}
int n,k,cnt,tot,t[M],ans[M];
inline void ad(int x,int val){wl(x<=k) t[x]+=val,x+=(x&-x);}
inline int ask(int x,int res=0){wl(x) res+=t[x],x-=(x&-x);return res;}
inline void cdq(int l,int r){
if(l==r) return void();
int Mid=(l+r)>>1,i=l,j=Mid+1;
cdq(l,Mid);cdq(Mid+1,r);
sort(a+l,a+Mid+1,c2);
sort(a+Mid+1,a+r+1,c2);
wl(j<=r){
wl(i<=Mid&&a[i].b<=a[j].b)
ad(a[i].c,a[i].num),i++;
a[j].res+=ask(a[j].c);j++;
}
rep(k,l,i-1,1) ad(a[k].c,-a[k].num);//清空
}
signed main(){
n=read(),k=read();
rep(i,1,n,1) b[i].a=read(),b[i].b=read(),b[i].c=read();
sort(b+1,b+1+n,c1);rep(i,1,n,1){
tot++;
if(!(b[i]*b[i+1]))
a[++cnt]=b[i],a[cnt].num=tot,tot=0;
}cdq(1,cnt);
rep(i,1,cnt,1)
ans[a[i].res+a[i].num-1]+=a[i].num;
rep(i,0,n-1,1) wr(ans[i]),pr(10);
return 0;
}
/*
*/
首先排序摁死第一维a,然后考虑只处理横跨左右两边的贡献点
将左右两边分别按照b排序
由于a被摁死了,所有左边的数的a无论怎么变都是小于右边数的a的
所以当b排序后,对左右首位作双指针,就只剩下c一维无序,使用权值树状数组查询即可
还有就是这道题有去重,要先遍历把重复的剖出来
inline void cdq(int l,int r){
if(l==r) return void();//边界条件
int Mid=(l+r)>>1,i=l,j=Mid+1;//取中点,双指针
cdq(l,Mid);cdq(Mid+1,r);//递归
sort(a+l,a+Mid+1,c2);//按照b排序
sort(a+Mid+1,a+r+1,c2);
wl(j<=r){//移动右指针
wl(i<=Mid&&a[i].b<=a[j].b) //左指针的b值一定要小于右指针的b值
ad(a[i].c,a[i].num),i++;//添加的价值是重复的数量
a[j].res+=ask(a[j].c);j++;//查询值域第三维
}
rep(k,l,i-1,1) ad(a[k].c,-a[k].num);//清空,每次都要
}
这个就是最基本的偏序问题,重要的是要看得出来
2. P3157 [CQOI2011] 动态逆序对
其实逆序对也是一个偏序问题,考虑一对有效逆序对的条件
i在j的前面,但i的权值比j的权值大,这就会对答案有贡献
现在是动态逆序对,其实也就是在pos,val维上再加一个del时间维
对这个东西做三维偏序统计答案即可
贴一个代码小技巧:
/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(ch,cr) for(auto ch:cr)
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
#define wl while
#define max(a,b)((a)>(b)?(a):(b))
#define min(a,b)((a)<(b)?(a):(b))
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=5e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
struct Node{int m,val,pos,id;}a[M];
//m->系数
//val->具体的值
//pos->位置
//id->删除的时间
//逆序对i,j要求:val[i]<val[j],id[i]>id[j],pos[i]>pos[j]
//val[i]>val[j],id[i]<id[j],pos[i]<pos[j]
inline bool c1(Node x,Node y){return x.pos<y.pos;}
int n,m,x,pos[M],t[M],ans[M];
inline void ad(int x,int va){wl(x<=n) t[x]+=va,x+=(x&-x);}
inline int ask(int x,int res=0){wl(x) res+=t[x],x-=(x&-x);return res;}
inline void cdq(int l,int r){
// cout<<"l:"<<l<<" r:"<<r<<'\n';
if(l==r) return void();
int Mid=(l+r)>>1,j=l;
cdq(l,Mid);cdq(Mid+1,r);
sort(a+l,a+Mid+1,c1);sort(a+Mid+1,a+r+1,c1);
rep(i,Mid+1,r,1){
wl(j<=Mid&&a[j].pos<=a[i].pos) ad(a[j].val,a[j].m),j++;
ans[a[i].id]+=a[i].m*(ask(n)-ask(a[i].val));
}
rep(i,l,j-1,1) ad(a[i].val,-a[i].m);
j=Mid;
dep(i,r,Mid+1,1){
wl(j>=l&&a[j].pos>=a[i].pos) ad(a[j].val,a[j].m),j--;
ans[a[i].id]+=a[i].m*(ask(a[i].val-1));
}
rep(i,j+1,Mid,1) ad(a[i].val,-a[i].m);
}
signed main(){
n=read(),m=read();
rep(i,1,n,1) a[i]=Node{1,read(),i,0},pos[a[i].val]=i;
rep(i,1,m,1) x=read(),a[n+i]=Node{-1,x,pos[x],i} ;
cdq(1,n+m);
rep(i,1,m,1) ans[i]+=ans[i-1];
rep(i,0,m-1,1) wr(ans[i]),pr(10);
return 0;
}
/*
*/
可以对所有元素维护一个系数,对答案的贡献可以用系数简化
比如这道题我用系数m=-1表示在这个时间删掉这个点
那么在这个位置上的权值就会是负数,对这个作前缀和就是该时间的答案
3. CF1045G AI robots
小技巧累计ing
每个rot有三个属性
但是这个位置很不好维护,还有就是智商是绝对值差值,如何三维偏序?
对这个东西考虑维护的距离实质
将原本的位置向左右扩展,只记录可以到达的位置
所以记一个rot的属性为[位置,视野,智商]
那么这个rot可以看到的范围就是[位置-视野,位置+视野]
那么考虑把这个玩意离散出来
一个rot可以看到的左右边界就会形象许多了
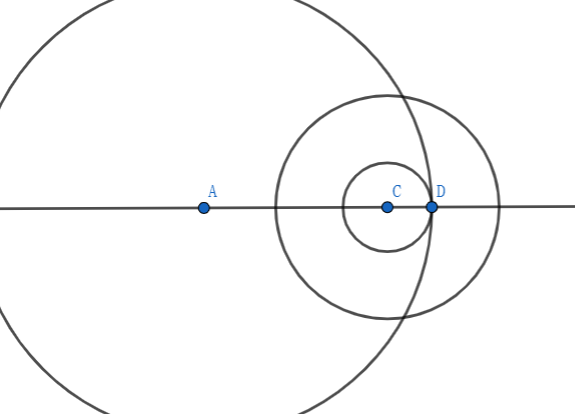

那么考虑对len一维排序,这样的化只要左边的家伙(len更小)可以看到右边的家伙,他们一定可以相互看到
/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(ch,cr) for(auto ch:cr)
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
#define wl while
#define max(a,b)((a)>(b)?(a):(b))
#define min(a,b)((a)<(b)?(a):(b))
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=1e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
int n,k,cnt,ans,t[M],Li[M];
inline void ad(int x,int val){wl(x<=n)t[x]+=val,x+=(x&(-x));}
inline int ask(int x,int res=0){wl(x)res+=t[x],x-=(x&(-x));return res;}
struct Node{
int lx,rx;
int pos,len,val;
}a[M];
inline void cdq(int l,int r){
if(l==r) return void();
int Mid=(l+r)>>1;
cdq(l,Mid);cdq(Mid+1,r);
int L=l,R=l-1;
rep(i,Mid+1,r,1){
wl(L<=Mid&&a[i].val-a[L].val>k) ad(a[L].pos,-1),L++;
wl(R<Mid&&a[R+1].val-a[i].val<=k) R++,ad(a[R].pos,1);
ans+=ask(a[i].rx)-ask(a[i].lx-1);
}
rep(i,L,R,1) ad(a[i].pos,-1);
sort(a+l,a+r+1,[&](Node x,Node y){return x.val<y.val;});
}
signed main(){
n=read(),k=read();
rep(i,1,n,1){
Li[i]=a[i].pos=read();
a[i].len=read();a[i].val=read();
}sort(Li+1,Li+1+n);cnt=unique(Li+1,Li+1+n)-Li-1;
rep(i,1,n,1)
a[i].lx=lower_bound(Li+1,Li+1+cnt,a[i].pos-a[i].len)-Li,
a[i].rx=upper_bound(Li+1,Li+1+cnt,a[i].pos+a[i].len)-Li-1,
a[i].pos=lower_bound(Li+1,Li+1+cnt,a[i].pos)-Li;
sort(a+1,a+1+n,[&](Node x,Node y){return x.len>y.len;});
cdq(1,n);wr(ans),pr(10);
return 0;
}
/*
*/
cdq内部再把val一维按死
在维护一个双指针的区间L,R保证其是合法区间
4. CF641E Little Artem and Time Machine
一样的偏序版子,考虑维护数删除时间,插入时间
对于每次的询问在时间t查x的数量
变成: \(插入时间<t,删除时间>t,权值=x\) 的三维偏序关系
5. P3658 [USACO17FEB] Why Did the Cow Cross the Road III P
小技巧ing
考虑每个玩意的属性
\(a \to 在左边的位置,b \to 在右边的位置,c \to 权值大小\)
那么合法的点对(i,j)就是
\(a_i<a_j,b_i>b_j(交叉),|c_i-c_j|\le k\)
直接开绝对值不好处理
可以掏两颗树状数组分别查大,查小
/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(ch,cr) for(auto ch:cr)
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
#define wl while
#define max(a,b)((a)>(b)?(a):(b))
#define min(a,b)((a)<(b)?(a):(b))
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=5e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
struct Node{
int a,b,c;
}a[M];
int t1[M],t2[M],n,k,ans;
inline void ad1(int x,int val){wl(x<=n)t1[x]+=val,x+=(x&(-x));}
inline int as1(int x,int res=0){wl(x) res+=t1[x],x-=x&-x;return res;}
inline void ad2(int x,int val){wl(x)t2[x]+=val,x-=(x&(-x));}
inline int as2(int x,int res=0){wl(x<=n) res+=t2[x],x+=x&-x;return res;}
inline void cdq(int l,int r){
if(l==r) return void();
int Mid=(l+r)>>1;
cdq(l,Mid);cdq(Mid+1,r);
sort(a+l,a+Mid+1,[&](Node x,Node y){return x.b>y.b;});
sort(a+Mid+1,a+r+1,[&](Node x,Node y){return x.b>y.b;});
int i=Mid+1,j=l;
wl(i<=r){
wl(j<=Mid&&a[j].b>a[i].b) ad1(a[j].c,1),ad2(a[j].c,1),j++;
if(a[i].c-k-1>=0) ans+=as1(a[i].c-k-1);
if(a[i].c-k+1<=n) ans+=as2(a[i].c+k+1);
i++;
}
rep(k,l,j-1,1) ad1(a[k].c,-1),ad2(a[k].c,-1);
}
int pl[M];
signed main(){
n=read(),k=read();
rep(i,1,n,1){
a[i].a=i;a[i].c=read();
pl[a[i].c]=i;
}
rep(i,1,n,1){
a[pl[read()]].b=i;
}
cdq(1,n);
wr(ans),pr(10);
return 0;
}
/*
*/
5 P4169 [Violet] 天使玩偶/SJY摆棋子
已知二位前缀和可以维护矩阵答案
cdq套cdq,高维偏序
更新中
cdq优化1d1d dp转移
更新中


 更新ing
更新ing

 浙公网安备 33010602011771号
浙公网安备 33010602011771号