斜二倍增喵
写在前面:
你必须学会斜二倍增,因为这是树上算法的[数据删除]!
写在中间:
斜二进制
和三进制很像,用 0,1,2 表示一个数,数位的权值为 \(2^k-1\)。
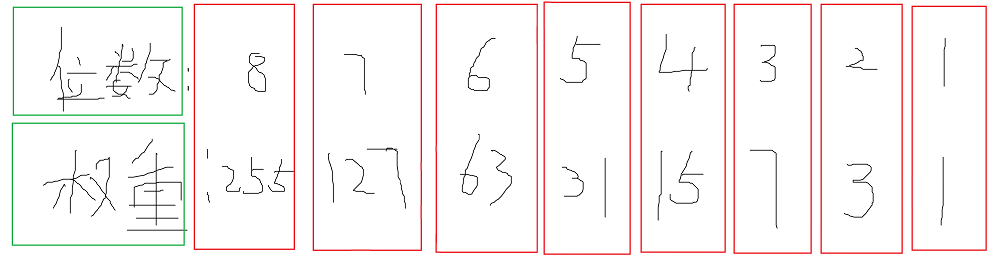
用斜二进制转换十进制,和二进制转十进制的原理是一样的
\(sum_{(10)}=\sum_{i=1}^{len}num_i\times w_i\)
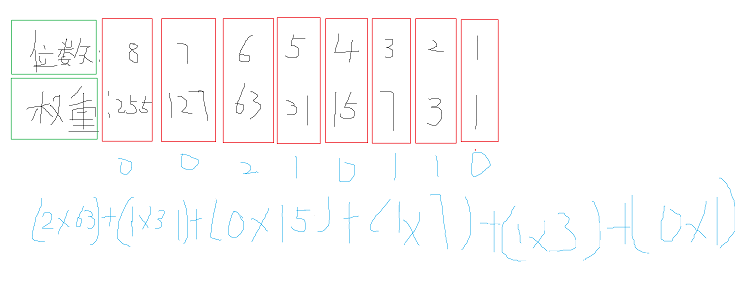
斜二转十
比如把斜二进制数 \(210110\)转化成十进制
$ sum=(2\times 63)+(1\times 31)+(0\times 15)+(1\times 7)+(1\times 3)+(0\times1)=167$
十转斜二
斜二进制有一个规定,每次十进制上的位置+1,转化到斜二进制上的表现是在每个末尾不为二的地方在末尾0处+1,为二时在二上+1进位。
这样的好处是不会有连续的二出现,可以顺序递推,举歌例子
\(\begin{align*}
1 & & 1\\
2 & & 2 & & \to 末尾为2\\
3 & & 10\\
4 & & 11\\
5 & & 12 & & \to 末尾为2\\
6 & & 20 & & \to 末尾为2\\
7 & & 100\\
8 & & 101\\
9 & & 102 & & \to 末尾为2\\
10 & & 110
\end{align*}\)
左边是十进制,右边是斜二进制。
斜二优化数据结构
对斜二进制数据结构有一个很形象的称呼,一大带二小
可以发现,由于斜二进制的位权值是二的整数幂次-1
所以可以拆分每段正幂次区间
比如在斜二进制下的数(7个0)(等号最右边是十进制)
\(10=1+1+1=2^{1-1}+2^{1-1}+1\)
\(100=10+10+1=2^{2-1}+2^{2-1}+1\)
\(1000000=1000000+1000000+1=2^{7-1}+2^{7-1}+1\)
转化成可视化就是像这样:
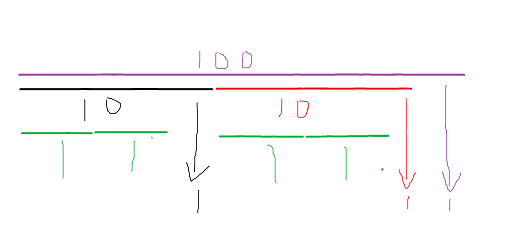
可以发现每个正幂次区间可以分割成 小+小+1 三个部分,对这个维护数据结构。
让最右边的1掌管这个区间的信息。
以区间查单点加为例
维护的东西:
- \(a_i\) 表示原本序列上的值
- \(sum_i\) 表示这一段区间维护的值
- \(fa_i\) 表示该点的上级节点
- \(lx_i\) 表示该点的左边界,即该点维护的信息在\((lx-1,i]\)左闭右开
inline void pushup(int x){//更新该点的信息
if(x-1==lx[x]) sum[x]=a[x];//只能控制自己
else sum[x]=a[x]+sum[x-1]+sum[lx[x-1]];//控制前两个
}
这个很好理解
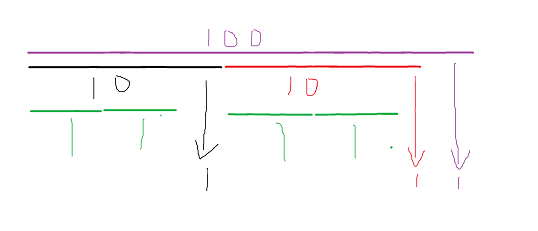
绿色的1只会找到自己,黑色红色1会找到两个绿色的1,紫色1会找到黑色红色的1
inline void ad(int x){//末尾追加
int p=mx,q=lx[mx++],r=lx[q];
// r q x
a[mx]=x;//加点
//如果是第一个||前两段不相等
if((!q)||((p-q)!=(q-r))) lx[mx]=mx-1;//只管辖自己
else fa[p]=fa[q]=mx,lx[mx]=r;//管辖前两段
pushup(mx);//更新权值
}
这个也很好理解,在末尾添加新的数据,会根据前两个再看本次的分类
inline void build(){//对于有值区间建树
rep(i,1,n,1){//本质上也是不断在后方加数
int p=i-1,q=lx[p],r=lx[q];
//一样的,第一个||前两段不想等
if((!q)||((p-q)!=(q-r))) lx[i]=i-1;
else fa[p]=fa[q]=i,lx[i]=r;//管辖前两段
pushup(i);//更新权值
}
}
对于区间的建树操作,理解了前文就会很简单
inline void upt(int pos,int val){//更新权值
a[pos]+=val;//首先更新原序列上的值
wl(pos){//不断向上
pushup(pos);//叶子被更新了,一层一层向上
pos=fa[pos];//去父亲哪里
}
}
由于斜二进制的权值可以看作\(2^k\) 所以可以看作为\(\log(n)\)的
inline int ask(int l,int r){
int res=0;
wl(l<=r){//一直跳
int x=lx[r];
if(x<l-1) res+=a[r],r--;//不能大跳就小跳
else res+=sum[r],r=x;//大跳!
}
return res;
}
每次向前\(\frac{2}{len}\),\(len<=n\),所以可以看作\(\log(n)\)
这也是斜二倍增的重点倍增优化,下面图论会再次详解.
例题P3374 【模板】树状数组 1
神秘邪恶倍增跑了759ms,树状数组跑了220ms,线段树500ms,分块550ms(((
斜二进制上树
代码很简单,就是把普通倍增的处理换成了斜二倍增,这个样子的:
inline void dfs(int u,int f){
int ff=lx[f],fff=lx[ff];
fa[u]=f;
if((Deep[f]-Deep[ff])==(Deep[ff]-Deep[fff]))
lx[u]=lx[ff];
else lx[u]=fa[u];
Deep[u]=Deep[f]+1;
for(auto v:Ed[u]){
if(v==f) continue;
dfs(v,u);
}
}
inline int lca(int a,int b){
if(a==b)return a;
wl(Deep[a]>Deep[b])
if(Deep[lx[a]]>Deep[b])
a=lx[a];
else a=fa[a];
wl(Deep[a]<Deep[b])
if(Deep[lx[b]]>Deep[a])
b=lx[b];
else b=fa[b];
wl(a!=b)
if(lx[a]!=lx[b]) a=lx[a],b=lx[b];
else a=fa[a],b=fa[b];
return a;
}
效果确实不错,在P3379 【模板】最近公共祖先(LCA)中:
斜二倍增:1.80s 在线 可动态加边
tarjan 2.10s 离线
普通倍增 3.63s 在线 可动态加边
树剖求lca 4.01s 在线
2. P14302 基础倍增练习题 6 / 小 U 的树
动态加边,强制在线,发现区间最大子段和可以左右合并
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define ll long long
#define ui unsigned int
#define ull unsigned long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(x,y) for(auto x:y)
#define wl while
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=3e6+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline ull read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(ull x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
ull sd;
inline ull rnd(){
sd^=sd<<13,sd^=sd>>7;
return sd^=sd<<17;
}
inline ull splitmix64(uint64_t x){
x+=0x9e3779b97f4a7c15;
x=(x^(x>>30))*0xbf58476d1ce4e5b9;
x=(x^(x>>27))*0x94d049bb133111eb;
return x^(x>>31);
}
int n,m;
struct Line{
int Next,To;
}Ed[M<<1];int Head[M],Tot=0;
inline void Adde(int u,int v){//加边
Ed[++Tot]=Line{Head[u],v};
Head[u]=Tot;
}
int fa[M];
inline int fid(int x){//并查集,维护连通块
if(x==fa[x]) return x;
return fa[x]=fid(fa[x]);
}
struct Node{
int id;
ll sum,mx,lx,rx;
inline Node operator +(const Node &x)const{//区间最大子段和
Node res;
res.id=id;//挂左边的id
res.sum=sum+x.sum;//总权值
res.lx=max(lx,sum+x.lx);
res.rx=max(rx+x.sum,x.rx);
res.mx=max(max(mx,x.mx),rx+x.lx);
return res;
}
}a[M],t[M];
int val[M],Deep[M],Siz[M];
inline void dfs(int u,int f){//初始化
a[u]=Node{f,val[u],val[u],val[u],val[u]};
int ff=t[f].id,fff=t[ff].id;//前面两个的位置
if((Deep[f]-Deep[ff])==(Deep[ff]-Deep[fff]))//是否相对
t[u]=(t[ff]+t[f])+a[u];//管一坨
else t[u]=a[u];//只管自己
Deep[u]=Deep[f]+1;
for(int i=Head[u];i;i=Ed[i].Next){
int v=Ed[i].To;
if(v==f) continue;
dfs(v,u);
}
}
inline ll ask(int x,int y){
Node res1={0,0,(int)(-INF),(int)(-INF),(int)(-INF)},res2=res1;
wl(Deep[x]>Deep[y]){//向上跳lca
if(Deep[t[x].id]>Deep[y]){
res1=t[x]+res1;
x=t[x].id;
}else{
res1=a[x]+res1;
x=a[x].id;
}
}
wl(Deep[x]<Deep[y]){
if(Deep[t[y].id]>Deep[x]){
res2=t[y]+res2;
y=t[y].id;
}else{
res2=a[y]+res2;
y=a[y].id;
}
}
wl(x!=y){
if(t[x].id!=t[y].id){
res1=t[x]+res1;
res2=t[y]+res2;
x=t[x].id;y=t[y].id;
}else{
res1=a[x]+res1;
res2=a[y]+res2;
x=a[x].id;y=a[y].id;
}
}
Node res=a[x];//树上路径,子段和要反转
swap(res1.lx,res1.rx);
res=res1+res;
res=res+res2;
return res.mx;
}
signed main(){
scanf("%d%d%llu",&n,&m,&sd);
sd=splitmix64(sd);
rep(i,1,n,1){
val[i]=(ui)rnd();
fa[i]=i;Siz[i]=1;
}
rep(i,1,n,1) dfs(i,0);
wl(m--){
int u=rnd()%n+1,v=rnd()%n+1;
int fu=fid(u),fv=fid(v);
if(fu==fv){
ll ans=ask(u,v);
sd^=ans;
}else{
if(Siz[fu]<Siz[fv]) swap(u,v),swap(fu,fv);
fa[fv]=fu;Siz[fu]+=Siz[fv];
Adde(u,v);Adde(v,u);
dfs(v,u);
}
}
printf("%llu\n",sd);
return 0;
}



 大份,邪恶倍增(
大份,邪恶倍增(

 浙公网安备 33010602011771号
浙公网安备 33010602011771号