Tarjan 与圆方树学习笔记
强连通分量
复习材料:link。
Tarjan 的关键是对于环来说,只有树边、返祖边、横叉边是有用的,前向边没有用。但是组成环的必要条件还是依靠树边与返祖边。
而其中,树边能直接继承儿子的 low 值,但返祖边、横叉边只能继承 dfn 值的原因是只要继承的 dfn 值,此时他就不会被当做一个 SCC 的根节点,而他前面的节点同样会被这个 dfn 值更新到(除了本身就是这个 dfn 值的节点)。
实际上 SCC 的 Tarjan 是可以把返祖边、横叉边继承 dfn 值改成把返祖边、横叉边继承 low 值的。只不过为了便于和其他 Tarjan 模板一起背,这里用 dfn 更新而已。
而不在栈中的横叉边不算(返祖边一定在栈中)的原因是此时这个边连向的点已经处于另一个 SCC 中,而那个 SCC 无法通过任何边走到这个节点的 SCC 的根,自然不能统计答案了。所以这个判断的意义就在于限制了只有在栈中的横叉边或者返祖边才能更新,而前向边是一直没有用的,根本不用更新。
时间复杂度 \(O(n+m)\)。
int scc[N],dfn[N],low[N],stk[N],tp,tot,cnt;
bitset<N>instk;
vector<int>g[N];
void tarjan(int u)
{
low[u]=dfn[u]=++tot;
instk[u]=1;stk[++tp]=u;
for(auto v:g[u])
{
if(dfn[v]==0)
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(instk[v])
{
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u])
{
int v;
cnt++;
do{
v=stk[tp--];
instk[v]=0;
scc[v]=cnt;
}while(u!=v);
}
}
割点
复习材料:link。
无向图与有向图不一样,无向图没有横叉边。在更新 low 的时候只有树边和返祖边会更新,前向边更新了和没更新一样。
注意判断割点的时机,是在走树边的时候。判断条件是 \(low_v \ge dfn_u, u\ne root\) 或 \(u=root,\sum [low_v \ge dfn_u]\ge 2\)。原因是根节点有可能是叶子结点,而叶子结点割掉是不会改变连通块个数的。
同时求割点是可以走反边来更新的,因为走反边只会被父亲的 dfn 更新,不会影响割点的判定。这也是为啥求割点不能用返祖边的 low 来更新,只能用返祖边的 dfn 来更新的原因,如果用 low 更新那么所有点的 low 都会因为反边追溯到根节点处,就判断不出来割点了。
注意每次进入一个连通块需要更新根节点。
时间复杂度 \(O(n+m)\)。
int root,dfn[N],low[N],tot;
vector<int>g[N];
bitset<N>cut;
void tarjan(int u)
{
dfn[u]=low[u]=++tot;
int child=0;
for(auto v:g[u])
{
if(dfn[v]==0)
{
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
child++;
if(u!=root||child>=2)cut[u]=1;
}
}
else
{
low[u]=min(low[u],dfn[v]);
}
}
}
割边
复习材料:link。
同样没有横叉边,大体和割点一样,判断的条件是 \(low_v>dfn_u\),判断时机和割点一样,但在更新 low 的时候多了一个限制:不能走反边。因为走了反边就会导致把 low 更新到父亲去,那么所有边都不是割边了。
同时因为叶子节点的边可以作为割边,所以不用特判根节点和满足要求的孩子个数,直接判断就能求出割边。
但是不能走反边的限制也让割边的实现有所不同,割边的实现上尽量写链式前向星,这样才能根据节点的编号判断反边(异或 \(1\) 后相等的是反边)。也正因如此,链式前向星的编号要从 \(2\) 开始,才能正确判断。
时间复杂度 \(O(n+m)\)。
注意,此处我把返祖边的 dfn 更新 low 值改成把返祖边的 low 值更新 low 值同样可以 AC 模板题,但是暂不清楚此写法是否可靠。
struct Edge{
int v,ne;
}e[N];
int n,m,h[N],idx=1,low[N],dfn[N],cnt,tot;
pi cut[N];
void add(int u,int v)
{
e[++idx]={v,h[u]};
h[u]=idx;
}
void tarjan(int u,int ineg)
{
dfn[u]=low[u]=++tot;
for(int i=h[u];i;i=e[i].ne)
{
int v=e[i].v;
if(dfn[v]==0)
{
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])cut[++cnt]={min(u,v),max(u,v)};
}
else if(i^1^ineg)
{
low[u]=min(low[u],dfn[v]);
}
}
}
这里借董晓 blog 的一张图:


不难发现,这三个模板都有着相同的架构,先走树边,用树边的 low 更新自己的 low,再走横叉边和返祖边,用他们的 dfn 更新自己的 low。
不同之处在于 SCC 中是在一个节点全遍历完,要 return 的时候用弹栈的方式求出 SCC 的。而割点和割边是在走树边的时候进行判断的,并且割点的判断条件是 \(low\ge dfn\),割边是 \(low>dfn\);割点中不需要判反边,但要判根节点,割边中要判反边,但不用判根节点。割边中最好利用链式前向星存图,初始边的编号从 \(2\) 开始。
边双连通分量
复习材料:link。
和求割边代码极其相似,唯一不同的是在进入的时候要把该节点入栈,在离开节点的时候判断该节点是否是一个边双连通分量的根,如果是的话就一直弹栈直到把这个连通分量弹空。整体和 Tarjan 求 SCC 比较像。
此处有割边其实就对应着子节点的一次弹栈。
在处理完边双后,缩完点的图的边全都是原图的割边,同时缩完点后的图形成一棵树(否则有环的话就还可以再缩点)。
时间复杂度 \(O(n+m)\)。
struct Edge{
int v,ne;
}e[M];
int n,m,h[N],idx=1,dfn[N],low[N],tot,stk[N],tp,cnt;
bitset<M>cut;
vector<int>edcc[N];
void add(int u,int v)
{
e[++idx]={v,h[u]};
h[u]=idx;
}
void tarjan(int u,int ineg)
{
dfn[u]=low[u]=++tot;
stk[++tp]=u;
for(int i=h[u];i;i=e[i].ne)
{
int v=e[i].v;
if(dfn[v]==0)
{
tarjan(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])cut[i]=cut[i^1]=1;
}
else if(i^1^ineg)
{
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u])
{
cnt++;
int v;
do{
v=stk[tp--];
edcc[cnt].push_back(v);
}while(v!=u);
}
}
点双连通分量
复习材料:link。
点双连通分量本质和求割点差不多,只不过在进入节点的时候要入栈,在发现 \(low_v \ge dfn_u\) 的时候要弹栈,注意此处不是发现割点再弹栈,而是满足条件就直接弹。因为不是割点的单个根节点所处的点双也是要算进去的,如果遇到割点再判就统计不到这个点双了。同时注意在弹栈的时候是弹到 \(v\) 为止,不要弹到 \(u\) 了,因为 \(u\) 是割点,它会被多个点双共享。
同时,注意特判孤立点与自环,尤其注意孤立点和自环结合的数据,此时需要记录某个点非自环的出边数量,只有这个值为 \(0\) 的时候才是孤立点,直接成一个单独的点双即可。
点双和边双的区别在于统计连通分量的时候,一个是在离开的时候统计,一个是在走树边的时候统计,这是因为点双所用的点会重复,而边双不会。
点双缩点后,建图是把整个点双看作节点,然后连所有割点向与包含它的点双的边,这个最终形成的形态是一棵树。这其实本质上就是圆方树了。
时间复杂度 \(O(n+m)\)。
int n,m,root,dfn[N],low[N],tot,stk[N],tp,cnt;
vector<int>g[N],vdcc[N];
bitset<N>cut;
void tarjan(int u)
{
low[u]=dfn[u]=++tot;
stk[++tp]=u;
int cb=0,child=0;
for(auto v:g[u])
{
if(dfn[v]==0)
{
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
child++;
if(u!=root||child>=2)cut[u]=1;
cnt++;
int x;
do{
x=stk[tp--];
vdcc[cnt].push_back(x);
}while(x!=v);
vdcc[cnt].push_back(u);
}
}
else
{
low[u]=min(low[u],dfn[v]);
}
if(v!=u)cb++;
}
if(cb==0)vdcc[++cnt].push_back(u);
}
再次借一下图:


这里图里给出的代码的 vdcc 是错误的,他没有特判孤立点与自环结合的情况。
SCC 和边双的共同之处是都是在离开的时候统计连通分量的,但点双是在走树边的时候统计的,并且还要特判自环和孤立点;SCC 与点双的共同之处是都用邻接表建图,而边双使用了链式前向星;边双和点双的共同之处是他们都是无向图,并且缩出来的图是树,而 SCC 是有向图,缩出来的图是 DAG。
圆方树
这个树基本就是点双的板子了,我们把 vdcc 看做方点,把原图上的点看做圆点,然后从每个 vdcc 的方点向他包含的点的圆点连边。
因此,圆方树有一个性质,那就是树上任何两条路径一定是圆点方点交替的。
还有一个常用性质,就是从某个点到另一点的路径的并集覆盖了路径上所有方点的 vdcc 所包含的圆点。这个也很显然吧。
那么圆方树的用途就是常用于处理连通性问题,尤其是有关于割点的问题。有时候还用于处理仙人掌,不过这个不咋考,就没学。
判断一个点是圆点方点的方法就是看他的 id 是否小于等于 \(n\) 即可。
做题时,我们常常会将圆方树上的节点赋上一个权值来处理路径问题,也常常会对圆方树上的圆点方点分讨处理连通性或者关于环的问题。
代码如下,在 vdcc 板子上改改就好了。注意圆方树的空间要开两倍,因为会多方点。
一个结论:对于原图上的一条边 \((u, v)\),它所在的点双为圆方树上 \(\text{LCA}(u, v)\) 所代表的点双(可以证明这个点一定是方点)。
int n,m,dfn[N],low[N],tp,stk[N],cnt,tot,root;
bitset<N>cut;
vector<int>g[N],g2[2*N];
void tarjan(int u)
{
dfn[u]=low[u]=++tot;
stk[++tp]=u;
int child=0,cd=0;
for(auto v:g[u])
{
if(dfn[v]==0)
{
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
child++;
if(child>=2||u!=root)cut[u]=1;
cnt++;
int x;
do{
x=stk[tp--];
g2[cnt].push_back(x);
g2[x].push_back(cnt);
}while(x!=v);
g2[cnt].push_back(u);
g2[u].push_back(cnt);
}
}
else
{
low[u]=min(low[u],dfn[v]);
}
if(u!=v)cd++;
}
if(cd==0)
{
cnt++;
g2[cnt].push_back(u);
g2[u].push_back(cnt);
}
}
常用结论
连通分量有以下常用结论:
- 边双连通分量
- 同一边双连通分量中,对于任意三个互不相同的点 \(a, b, c\),必定存在一条不经过重复边的路径,按顺序经过了 \(a, b, c\) 三个点,即路径为 \(a \to b \to c\)。
- 同一边双连通分量中,对于任意两个不相同的点 \(a, b\) 和一条边 \(e\),必定存在一条不经过重复边的路径,按顺序经过了 \(a, e, b\) 三个点或边,即路径为 \(a \to e \to b\)。
- 边双连通分量缩点后的形态是一棵树。
- 同一边双连通分量中,对于任意两个不同的点 \(a,b\),他们之间不经过重复边的路径的并集,恰好完全等于这个边双连通分量。
- 点双连通分量
- 同一点双连通分量中,对于任意三个互不相同的点 \(a, b, c\),必定存在一条不经过重复点的路径,按顺序经过了 \(a, b, c\) 三个点,即路径为 \(a \to b \to c\)。
- 同一点双连通分量中,对于任意两个不相同的点 \(a, b\) 和一条边 \(e\),必定存在一条不经过重复点的路径,按顺序经过了 \(a, e, b\) 三个点或边,即路径为 \(a \to e \to b\)。
- 每个点双连通分量可以用一个方点代替,原图中的节点用圆点代替,可以利用圆方树解题。
- 一个点可能属于多个点双连通分量,此时这个点在圆方树上时是非叶子节点。
- 同一点双连通分量中,对于任意两个不同的点 \(a,b\),他们之间不经过重复点的路径的并集,恰好完全等于这个点双连通分量。
- 点双连通分量的定义是不含割点的极大连通分量,边双连通分量的定义是不含割边的极大连通分量。因此点双连通分量一般一定是边双连通分量,点双的限制一般是更强的。但是需要注意两点连边的特殊情况,此时是点双连通分量不是边双连通分量,做点双题目的时候一定要特殊考虑一下这种情况。上述结论同样也是不考虑两点连边这种特殊情况的。
下面对部分结论进行证明:
- 边双连通分量的结论 \(1\)

- 考虑这张图,根据边双的定义,\(a,b\) 之间一定存在至少两条不交的路径。于是可以先走与 \(c\) 的连接点(即点 \(1\))不交的一条路径 \(a\to 4 \to 3 \to b\),然后再走与 \(c\) 的连接点相交的路径 \(b\to 2 \to 1 \to 5 \to c\) 即可。若 \(1\) 与 \(a\) 重合也是成立的,因为只需要保证不经过重复边即可。
- 边双连通分量的结论 \(2\)
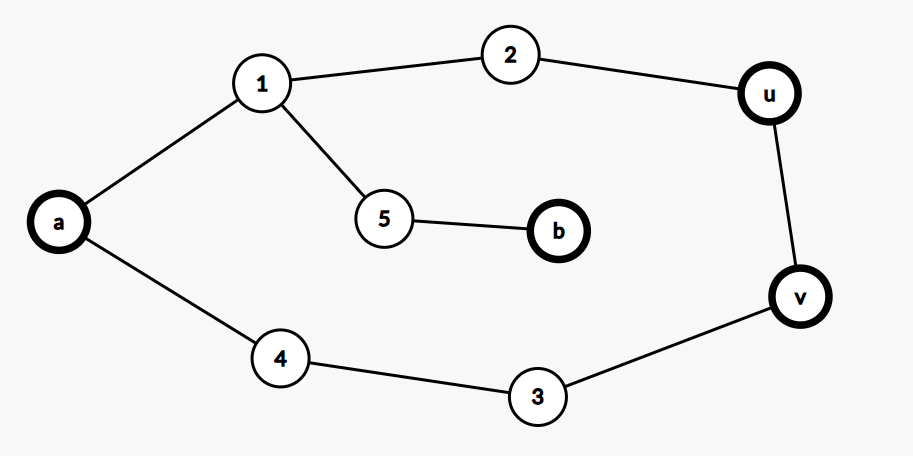
- 考虑这张图,利用一个经典技巧:边转点。在边 \(e\) 的两端点 \(u, v\) 之间新建一个叫 \(c\) 的点。

- 不难发现加了这样一个点后该图依然是边双,于是问题转化为证明存在一条不经过重复边的经过 \(a \to c \to b\) 的路径。可以直接利用结论 \(1\) 来证明。
- 边双连通分量的结论 \(4\)
- 考虑枚举每条边,问题转化为证明对于每条边 \(e\),不经过重复边的路径 \(a\to e \to b\) 都存在。然后运用结论 \(2\) 即可证明。
- 点双连通分量的结论证明和边双几乎一样,此处不再赘述。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号