D16 割点 Tarjan 算法

D16 割点 Tarjan 算法_哔哩哔哩_bilibili

 

割点和桥 - OI Wiki

在一张连通的无向图中，对于两个点 𝑢 和 𝑣，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 𝑢 和 𝑣 边双连通．

在一张连通的无向图中，对于两个点 𝑢 和 𝑣，如果无论删去哪个点（只能删去一个，且不能删 𝑢 和 𝑣 自己）都不能使它们不连通，我们就说 𝑢 和 𝑣 点双连通．

对于一个无向图中的 极大 边双连通的子图，我们称这个子图为一个 边双连通分量．

对于一个无向图中的 极大 点双连通的子图，我们称这个子图为一个 点双连通分量．

对于一张连通的无向图，我们可以从任意一点开始 DFS，得到原图的一棵 DFS 生成树（以开始 DFS 的那个点为根），这棵生成树上的边称作 树边，不在生成树上的边称作 非树边．由于 DFS 的性质，所有非树边连接的两个点在生成树上都满足其中一个是另一个的祖先．

割点

对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）．

过程

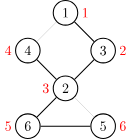
我们按照 DFS 序给他打上时间戳 dfn （访问的顺序）．

还需要另外一个数组 low，用它来存储不经过其父亲能到达的最小的时间戳．

例如 low[2] 是 1，low[5] 和 low[6] 是 3．

判断某个点是否是割点：对于某个顶点 𝑢，如果存在至少一个儿子 𝑣，使得 𝑙𝑜𝑤_𝑣 ≥𝑑𝑓𝑛_𝑢，即 𝑣 不能回到 𝑢 的祖先，那么 𝑢 点为割点．

例如 low[6]=3=dfn[2]，说明 2 为割点．

对于根节点的判断，需要存在至少两个儿子 𝑣，使得 𝑙𝑜𝑤_𝑣 ≥𝑑𝑓𝑛_𝑢．理由如图，根节点 1 只有一个儿子 2 满足条件，故 1 不是割点．

注意：若 v 已访问，必须用 dfn[v] 更新 low[u]。否则，因为边是双向的，儿子会用父节点的 low 更新，最终每个点的 low =1，无法判割点。

P3388 【模板】割点（割顶） - 洛谷

// Tarjan 算法 O(n+m)
#include<bits/stdc++.h>
using namespace std;

const int N=20010;
int n,m;
vector<int> e[N];
int dfn[N],low[N],tim,cut[N],root;

void tarjan(int u){
  dfn[u]=low[u]=++tim;
  int son=0; //u的儿子个数
  for(int v:e[u]){
    if(!dfn[v]){ //若v未访问
      tarjan(v);
      low[u]=min(low[u],low[v]);
      
      if(low[v]>=dfn[u]){ //说明儿子v没有连通u的祖先
        ++son;
        if(u!=root||son>1) cut[u]=1; //u不是根需要1个儿子，是根需要2个儿子
      }
    }
    else //若v已访问
      low[u]=min(low[u],dfn[v]); //注:dfn不能换成low
  }
}
int main(){
  cin>>n>>m;
  for(int a,b;m--;){
    cin>>a>>b;
    e[a].push_back(b),
    e[b].push_back(a);
  }
  for(root=1;root<=n;root++) if(!dfn[root]) tarjan(root);
  
  int ans=0;
  for(int i=1;i<=n;i++) if(cut[i]) ans++;
  cout<<ans<<"\n";
  for(int i=1;i<=n;i++) if(cut[i]) cout<<i<<" ";
}

 

P3469 [POI 2008] BLO-Blockade - 洛谷

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N=100010;
int n,m,a,b;
vector<int> e[N];
int dfn[N],low[N],tim,cut[N],siz[N],ans[N];

void tarjan(int x){
  dfn[x]=low[x]=++tim; siz[x]=1;
  int son=0,sum=0;
  for(int y:e[x]){
    if(!dfn[y]){ //若y未访问
      tarjan(y);
      low[x]=min(low[x],low[y]);
      siz[x]+=siz[y];
      if(low[y]>=dfn[x]){
        // son++;
        // if(x!=1||son>1) cut[x]=1;
        ans[x]+=siz[y]*(n-siz[y]); //y子树的贡献
        sum+=siz[y];
      }
    }
    else low[x]=min(low[x],dfn[y]);
  }
  ans[x]+=(n-sum-1)*(sum+1); //x子树外的贡献
  ans[x]+=n-1; //x的贡献
}
signed main(){
  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  cin>>n>>m;
  while(m --){
    cin>>a>>b;
    e[a].push_back(b),
    e[b].push_back(a);
  }
  tarjan(1);
  for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
}