D14【模板】强连通分量 Tarjan 算法

D14【模板】强连通分量 Tarjan 算法_哔哩哔哩_bilibili

 

强连通分量 - OI Wiki

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通．

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图．

在有向图中求强连通分量的 Tarjan 算法．

                            

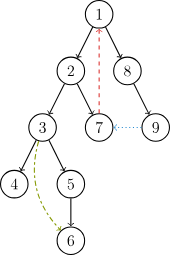
有向图的 DFS 生成树主要有 4 种边：

1. 树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边．
2. 反祖边（back edge）：示意图中以红色边表示（即 7 →1），也被叫做回边，即指向祖先结点的边．
3. 横叉边（cross edge）：示意图中以蓝色边表示（即 9 →7），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先．
4. 前向边（forward edge）：示意图中以绿色边表示（即 3 →6），它是在搜索的时候遇到子树中的结点的时候形成的．

考虑 DFS 生成树与强连通分量之间的关系．

如果结点 𝑢 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 𝑢 为根的子树中．结点 𝑢 被称为这个强连通分量的根．

每个连通分量为搜索树中的一棵子树，在搜索过程中，维护一个栈，每次把搜索树中尚未处理的节点加入栈中．

在 Tarjan 算法中为每个结点 𝑢 维护了以下几个变量：

1. 𝑑𝑓𝑛_𝑢：深度优先搜索遍历时结点 𝑢 被搜索的次序．
2. 𝑙𝑜𝑤_𝑢：在 𝑢 的子树中能够回溯到的最早的已经在栈中的结点的 𝑑𝑓𝑛 的最小值．
   𝑙𝑜𝑤_𝑢 为以下结点的 𝑑𝑓𝑛 的最小值：从以 𝑢 为根的子树 𝑆𝑢𝑏𝑡𝑟𝑒𝑒_𝑢 通过反祖边或横叉边能到达的结点．

从根开始的一条路径上的 dfn 严格递增，low 严格非降．

搜索过程维护每个结点的 dfn 与 low 变量，且让搜索到的结点入栈 stk．每当找到一个强连通分量 scc，就让栈中元素出栈．

在搜索过程中，对于结点 𝑢 和与其相邻的结点 𝑣（𝑣 不是 𝑢 的父节点）考虑 3 种情况：

1. 𝑣 未被访问：继续对 𝑣 进行深度搜索．在回溯过程中，用 𝑙𝑜𝑤_𝑣 更新 𝑙𝑜𝑤_𝑢．因为存在从 𝑢 到 𝑣 的直接路径，所以 𝑣 能够回溯到的已经在栈中的结点，𝑢 也一定能够回溯到．
2. 𝑣 被访问过，已经在栈中：根据 low 值的定义，用 𝑑𝑓𝑛_𝑣 更新 𝑙𝑜𝑤_𝑢．
3. 𝑣 被访问过，已不在栈中：说明 𝑣 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作．

分量标号和拓扑序的关系：在缩点后的 DAG 中，强连通分量（缩点后）的标号顺序是其拓扑序的逆序．

P2863 [USACO06JAN] The Cow Prom S - 洛谷

// Tarjan算法 O(n+m)
#include<bits/stdc++.h>
using namespace std;

const int N=10010;
int n,m,ans;
vector<int> e[N]; 
int dfn[N],low[N],tim,stk[N],top,scc[N],siz[N],cnt;

void tarjan(int u){
  dfn[u]=low[u]=++tim; stk[++top]=u;
  for(int v:e[u]){
    if(!dfn[v]){ //若v尚未访问
      tarjan(v);
      low[u]=min(low[u],low[v]);
    }
    else if(!scc[v]) //若v已访问且未构成SCC
      low[u]=min(low[u],dfn[v]);
  }

  if(low[u]==dfn[u]){ //若u不是SCC的根，则low<dfn
    ++cnt;
    for(int v=-1;v!=u;){
      v=stk[top--];
      scc[v]=cnt; //SCC的编号
      ++siz[cnt]; //SCC的大小
    }
  }
}
int main(){
  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  cin>>n>>m;
  for(int a,b;m--;) cin>>a>>b,e[a].push_back(b);
  for(int i=1;i<=n;i++)if(!dfn[i]) tarjan(i);
  for(int i=1;i<=cnt;i++)if(siz[i]>1) ans++;
  cout<<ans;
}

 

B3609 [图论与代数结构 701] 强连通分量 - 洛谷