电机控制笔记:理解直流无刷电机矢量控制
电机原理
有刷电机原理
工作原理:
通电线圈会产生磁场,方向符合右手螺旋定则. 如果将通电线圈放在2个固定的永磁体磁极之间,在2个磁场力的作用下,线圈会移动.
如果在中空的圆柱体形状之间放置2个永磁体,且使它们的南北极相对,中间放置通电线圈,根据右手螺旋定则,线圈两端会产生N、S 2个磁极. 在2个磁场力(永磁体)的作用下,线圈的一个磁极被吸引,另一个磁极被排斥,线圈会朝一个方向旋转,直到通电线圈的磁极方向与南北极磁极方向相反,线圈N极被永磁体S级吸引,S极被永磁体N极吸引.
此时,如果改变电流方向,则线圈的磁极对换,被吸引的磁极由于磁场方向,会被排斥,从而促使线圈产生新一轮转动.
组成:
有刷直流电机由定子、换向器、电刷、转子组成. 定子固定不动,一般由永磁体制作.
- 定子,由通电线圈产生磁场,以便控制磁场强度、方向.
- 换向器,负责在特定位置改变电流方向,使产生的磁场始终和定子磁场保持一定角度,在磁场相互之间力的作用下,转子会做旋转运动.
下图是直流有刷电机示意图:
电流通过电刷换向,形成磁场,与定子磁场相互作用,带动转子旋转.
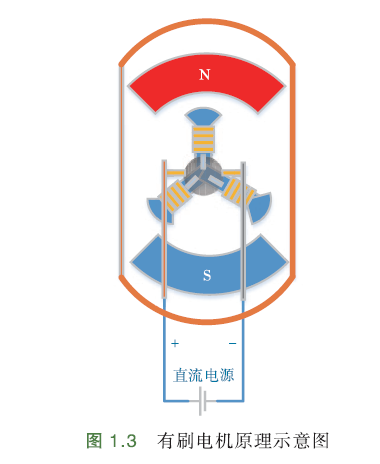
直流有刷电机采用电刷换向,
- 缺点:容易出现磨损、寿命短、接触点容易产生灰尘、噪声大;
- 优点:结构简单,励磁方向始终与定子磁场方向保持一定角度,因此转矩大、控制方法简单. 调速性能好,改变直流供电电压,流过线圈的电流变化,产生的磁场强度也会变化,磁场力也会随之改变.
无刷电机原理
无刷直流电机控制,用电力电子器件代替电刷,用Hall传感器实时检测转子位置,根据传感器状态控制电力电子器件的通断,从而进行换向.
也有很多直流无刷电机没有安装检测位置的传感器,而是依赖电机的运动关系、磁链方程,通过观测器估算转子位置,从而进行有效控制.
无刷直流电机一般设置为三相,有些小家电为了省成本,只设置两相.
下图是直流无刷电机内部结构示意图:
简单画出三相定子的3个线圈,实际线圈是多组对称缠绕方式:
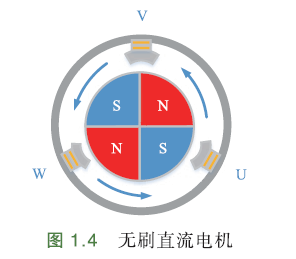
图中,定子U、V、W为无刷直流电机的三相线圈,转子为永磁体.
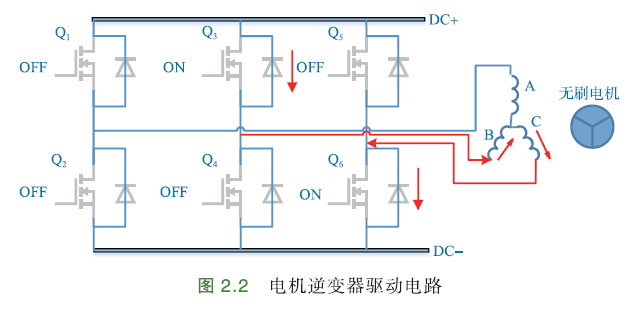
典型的无刷直流电机逆变器驱动电路:
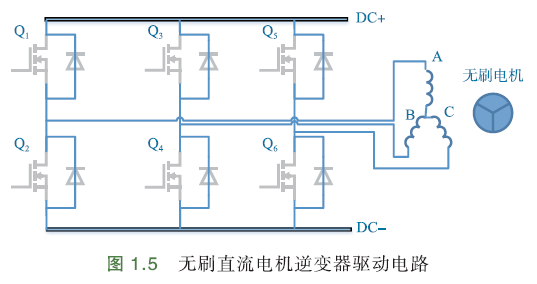
原理是通过控制功率管的通断,来控制电机的电流、方向.
缺点:控制成本比有刷电机高;
优点:寿命长、噪声小,不产生粉尘,过载能力强,调速范围广,线性度好,应用广泛.
方波控制
Hall传感器、电机换向
开关型Hall传感器是磁场敏感元件,经过NS极时输出信号会出现高低电平变化. 将Hall严格按定子换向边放置,当定子换向时,Hall输出电平高低变化,就能检测到定子换向.
一对极(磁极对数量为1)电机的Hall安装位置如下图:
每个电机只需要3个Hall,间隔120°电角度摆放,就能准确检测定子三相的换向时刻. 也有按60°电角度摆放的,hall输出顺序不同,但原理相同.
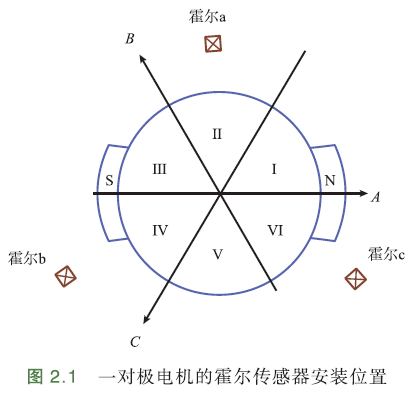
注意:这里Hall安装位置与电机控制笔记:BLDC控制原理这篇文章中的不一样
每当hall经过磁极时,输出状态改变一次. 磁场旋转一个电周期,每个hall改变2次输出状态,3个hall共改变6次输出状态.
电角度指磁场旋转角度,电周期指磁场旋转周期.
方波控制原理
方波驱动时,每次只给三相电机中的2相通电:一相连电源+,一相连电源-,一相浮空.
假设某一时刻,与A相连的2个功率管Q1、Q2关断,电机A相浮空;与B相连的上桥Q3导通,下桥Q4关断,B连到电源+;与C相连的上桥Q5关断,下桥Q6导通,C连接到电源-.
于是,电流流向:电源+ -> Q3 -> B相 -> C相 -> Q6 -> 电源-
注意:为了避免短路,上下2个功率管不能同时导通,如Q1、Q2.
通电线圈产生磁场,在定子磁场的作用下,转子会产生一定角度的旋转. 如果此时根据hall的输出状态,改变功率管的开通顺序,转子会持续转动到下一个位置.
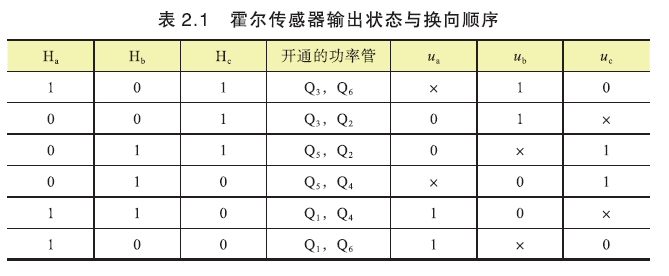
根据hall的输出状态,按下表周期性通电,那么转子会不停地从一个位置运动到另一个位置,从而周期性地旋转. 每次改变通电顺序,称为一次换向,一个电周期需要6次换向.
—— 这就是通常说的六步换向.
旋转时,定子、转子磁场始终保持适当角度差,要使电机产生的力矩增大,可以适当调整定子磁场领先转子磁场的角度.
由于Hall传感器安装位置,不同电机可能不一样,因而对应的换相真值表不同. 电机厂商通常会给出配套电机的真值表(逆时针旋转),如下表:
注意:该表基于Hall传感器与相线圈的安装位置,脱离Hall安装位置讨论真值表无意义.
逆时针旋转时,hall输出状态与各相通电顺序:5->1->3->2->6->4. (1,2,3,4,5,6指上表Ha、Hb、Hc组合值,1=0b001, 2=0b010, 3=0b011, 4=0b100, 5=0b101, 6=0b110)
顺时针旋转时,顺序相反:4->6->2->3->1->5
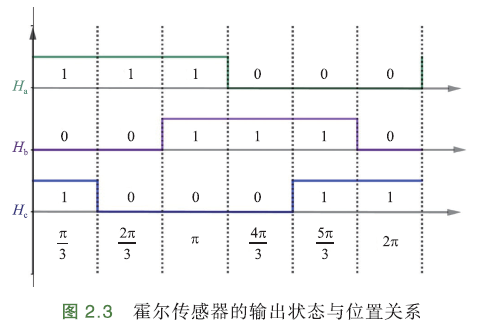
hall输出状态,会随着转子移动而改变. 三相间隔120°电角度摆放,3个hall输出信号波形也相差120°电角度.
每个hall的输出状态每隔180°改变一次,三相hall将整个平面划分为6个扇区,每隔60°电角度,3个hall的输出状态组合改变一次.
导通的功率管的PWM占空比 => 平均电压 => 直流电机转速 ∝ 电压
常见PWM调节方式:
1)H_PWM/L_ON,其中一相下桥臂一直开通,只调节另一相的上桥臂. 如第一个状态,Ua给+,Uc给-,Q3、Q6导通,电流从电源+ -> Q3 -> B相 -> C相 -> Q6 -> 电源- . 此时,只用调节Q3占空比,Q6一直打开.
2)H_ON/L_PWM,与方式1相反,其中一相上桥臂一直开通,只调节另一相的下桥臂.
3)H_PWM/L_PWM,两相桥臂对应的功率管互补调节. 例如,某个区间内,Q3、Q4为一组互补输出,Q5、Q6为一组,Q1、Q2关断. 互补好处:上管关断瞬间电流可由下管续流,而不经过功率管的内部续流二极管,可避免大电流损害功率管.
PWM频率一般20KHz,原因:1)功率管能力有限;2)尽量避免高次谐波干扰.
方波控制缺点
1)发热
方波驱动时,电机相电流只有通、断两种状态,即使占空比很小、平均电流很小,线圈电流的峰值电流也会很大. 因为发热量∝\(I^2\),所以方波控制的系统发热量大,能量损耗大.
2)不稳定
方波控制的磁场不连续,是跳跃的,因此会造成转矩的脉动. 对转矩要求高的场合,方波控制不合适,会造成系统不稳定,控制精度低.
3)噪声
转矩的脉动会造成系统振动,产生噪声,干扰系统本身的稳定性,使得芯片、传感器性能下降
优点:控制算法简单、硬件成本低
矢量控制
概述
传统三相交流电机,输入的是三相对称正弦电流,空间磁链近似圆形,转矩稳定. 但有缺点:
1)三相对称正弦电流,产生的是一个随时间、空间变化的旋转磁场,是一个多变量的系统;
2)转子磁势、定子磁通之间不存在垂直关系;
3)定子电流无法单独调节励磁、转矩,它们之间是强耦合、非线性的复杂关系;
4)体积大、损耗大.
能否将三相交流感应电机像直流电机那样,控制简单有效、稳定?
为解决该问题,有人提出一种矢量控制方式,将三相交流信号经过一系列坐标变换,最终变成直流可控的两相正交电流. 如此,解耦了复杂的电流关系,使得交流电机简单可控.
矢量控制技术可用于交流电机控制、直流无刷电机控制.
不论哪种电机,转矩∝定子磁场和转子磁场的叉积,即它们围成的平行四边形面积
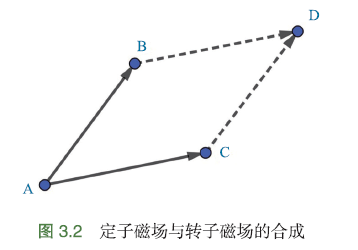
当定子磁场⊥转子磁场时,平行四边形面积最大,产生的力矩最大
原理
正弦波控制,介于方波控制与矢量控制,是一种PWM调制技术,将方波PWM按正弦方式调制. 能得到定子正弦电流,但只能控制电流大小,不能控制方向.
矢量控制能控制电流大小,也能控制方向. 矢量控制,也叫磁场定向控制(Field-Oriented Control,FOC),核心是解耦复杂的定子电流关系,将定子电流分解成控制励磁的直轴电流、控制转矩的交流电流.
三相电机的三相正弦电流\(i_a,i_b,i_c\),相位差120°,在空间形成旋转磁场. 假设产生的旋转磁动势F,且与电流同步,以角速度ω逆时针旋转.
要在空间上产生旋转磁动势,不一定要三相对称绕组,任意对称的多相绕组都可以. 为简单起见,可将三相电机模型想成两相电机模型:两相空间互差90°,产生和三相电机相同的选择磁动势.
等效模型如下:
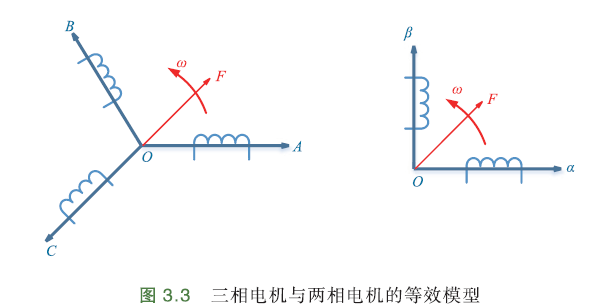
三相(a,b,c)对称绕组产生的磁场、力矩(大小、方向) = 两相(α,β)正交绕组,且以同样角速度逆时针旋转. 这就是 三相静止坐标到两相静止坐标的变换,简称3s/2s变换(s=static).
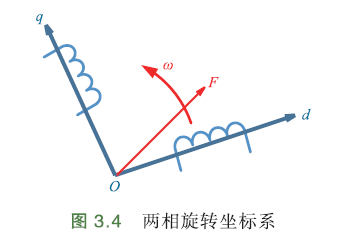
假设有一个两相正交的对称绕组,分别通入直流电流\(i_d,i_q\),产生的合成磁动势,和两相静止坐标系及三相静止坐标系完全相等,且以与磁动势相同角速度ω旋转,那么dq旋转坐标系和前面静止的三相abc坐标系、两相αβ坐标系等效. 这就是 两相静止坐标系到两相旋转坐标系的变换,简称2s/2r变换(r=rotation).
合成矢量的推导、克拉克变换
设三相对称正弦电路:
其中,\(I_m\)幅值,\(ω=2πf\)角速度,三相电流相位差120°.
合成电流如下图:
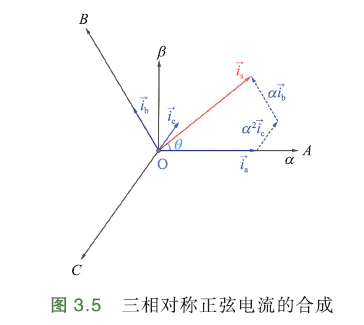
- 合成矢量推导
电流合成矢量:
根据欧拉公式\(e^{jx}=cosx+jsinx\):
∴空间上互差120°的三相对称正弦电流的合成矢量是一个角速度ω、绕中心点旋转的矢量,因此形成旋转磁场,幅值=3/2*单相幅值
- 克拉克变换
Clarke变换:A、B、C三相静止坐标系到α、β两相静止坐标系的变换过程.
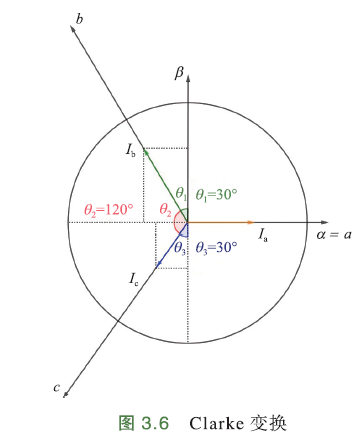
将三相电流\(I_a,I_b,I_c\)投影到\(α,β\)轴:
矩阵形式:
- 等幅值变换
设变换前电流有效值\(I_m\),根据前面三相合成公式,变换后有效值\(\frac{3}{2}I_m\).(对电压也适用)
为保证变换前后幅值不变(等幅值),即合成矢量大小、方向相等,变换时需要乘一个系数k.
∴\(k=\frac{2}{3}\)
证明过程可参见:FOC算法笔记 等幅值变换形式
于是,克拉克变换的等幅值变换形式:
再由基尔霍夫电流定律\(I_a+I_b+I_c=0\),
- 等功率变换
假设变换前功率\(P_0\),变换后功率\(P_1\),有
令\(P_0=P_1\),可得\(k=\sqrt \frac{2}{3}\)
帕克变换
矢量控制核心:解耦复杂电流关系. 克拉克变换将三相边两相,电流依然由时间、速度决定. 还需要进一步变换,将αβ轴决定的两相静止坐标系变换为随磁场旋转的dq坐标系.
—— 这就是帕克变换(Park).
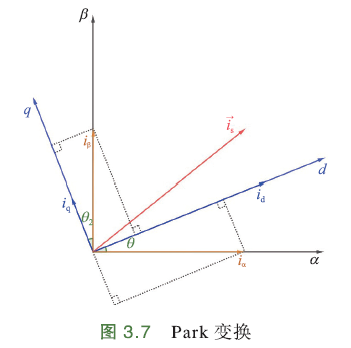
\(i_α,i_β\)是合成矢量\(\overrightarrow{I_s}\)在α、β决定的两相静止坐标轴上的投影. \(d-q\)坐标系是随转子磁场旋转坐标系,q轴⊥磁场,称为交轴;d轴//磁场,称为直轴.
角度θ是d轴与α轴夹角. 根据三角关系,\(i_α\)在d轴投影\(i_α cosθ\),q轴与β轴夹角\(θ_2\),可得\(θ_2=θ\)
下图描述了克拉克变化、帕克变换的电流波形:
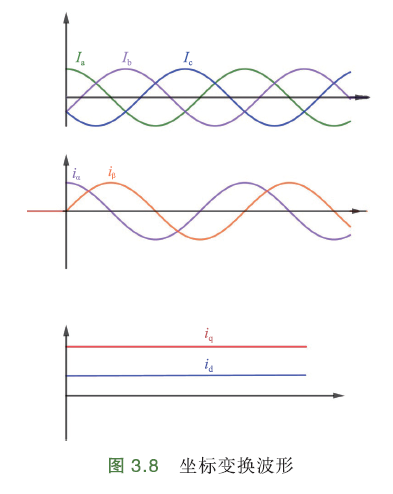
d-q轴数学方程
永磁同步电机的动态数学模型是非线性、多变量的,在考虑数学模型时,需要设定以下条件:
1)忽略转子、定子的磁饱和现象,磁滞损耗和涡流损耗等;
2)假定转子采用无阻尼绕组,定子的各项物理性能在外界条件变化时不变化;
3)假定转子永磁体的电导率0,且假定转子内部磁导率0;
4)假定稳态运行时,三相绕组中感应电动势为标准正弦波;
5)忽略磁场中所有谐波;
6)各项绕组对称分布,绕组匝数相同,轴线相互之间的位移电角度相同.
三相对称、空间互差120°,每个绕组电压、电阻、磁通变化等都是平衡的.
基于此,永磁同步电机在两相旋转坐标系下的数学模型可表示为以下方程.
磁链方程:
电压方程:
其中,\(ψ,i,u\)分别为磁链、电流、电压;\(ψ_f\)永磁体磁链;\(R_s\)定子相电阻;\(L_d,L_q\)分别为d、q轴同步电感;\(ω\)角速度.
磁链指穿过线圈的总磁通量.
其中,线圈匝数N,单匝线圈磁通量Φ
电机稳定运行时,假设d、q轴稳态电压、电流分别为\(u_d,u_q\)和\(i_d,i_q\),忽略电阻压降,有:
注意:稳态说明电感压降为0
则d-q坐标系下转矩方程:
d-q坐标系下运动方程:
其中,J转动惯量;ω角速度;\(τ_{em}\)转矩;\(τ_L\)负载转矩;\(p_n\)极对数;B黏滞摩擦系数.
稳态下,电机等效电路可看成电阻和电感的串联,再假设一个反相电动势. 如下图:
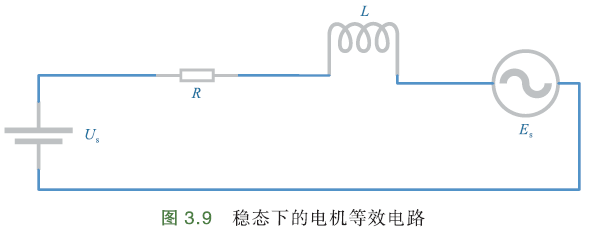
R等效电阻,L绕组电感,\(e_s\)反电动势.
电压矢量方程:
常见矢量控制算法:最大转矩法、弱磁控制法、恒功率因素控制法、\(i_d=0\)矢量控制法.
其中,\(i_d=0\)矢量控制法应用较多,但要求为简单FOC应用.
\(i_d=0\)时,转矩方程变成:
此时,定子电流矢量d轴分量为0,全部电流都用于转矩控制,转子磁场空间矢量和定子磁动势空间矢量正交. 电机电压矢量利用率最大,控制转矩只需要控制\(i_q\)大小即可.
矢量控制架构
帕克变换后,三相强耦合、非线性、复杂关系的电流变换成随磁场旋转的d-q轴电流,可分别控制转矩、励磁,从而解耦.
下面实现\(i_d=0\)矢量控制法.
首先,电机控制 <=> 力的控制 <=> 电流控制. 有控制,就有反馈、有闭环,力矩控制通过q轴电流控制实现,所以矢量控制先有电流控制环.
矢量控制架构:
电流环外部是速度环,通过安装在电机底部的位置传感器,或者无感观测器算法获得转子位置信息,并计算反馈速度,与给定速度比较,结果送入速度PI控制器,控制转矩电流输出.
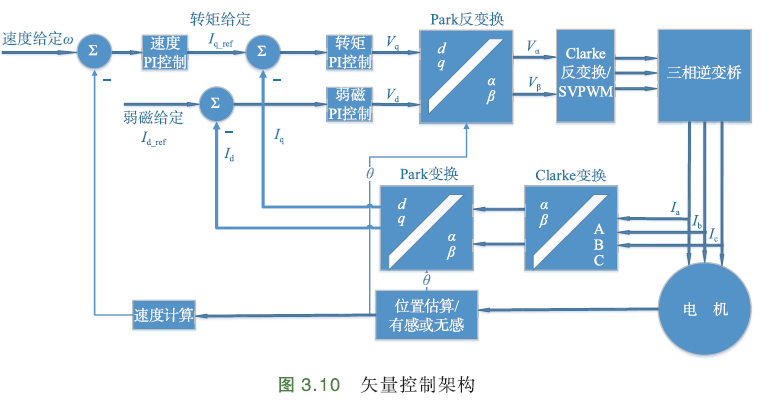
然后,转矩电流进入电流环转矩PI控制器,便于输出dq轴电压. 不过,该电压无法直接驱动电机,需将dq坐标系下的电压经 帕克反变换、克拉克反变换,变换为ABC三相电压,再来驱动电机.
为什么让d轴电流\(i_d=0\),只控制q轴电流?
因为d轴电流对转矩没有贡献. 可以最大化利用电流. \(i_d=0\)矢量控制法简单、高效.
相电压与线电压
相电压(Phase Voltage)指电机某一相(A、B或C)两端相对于电机中性点(三相绕组公共连接点)的电压.
如果中性点不存在,相电压指绕组两端电压.
例如:A相与中性点N之间电压\(V_{AN}\)
各相对中性点的电压,幅值相等,相位差120°. 用相量法表示相电压:
其中,\(V_p\)相电压幅值;\(V_p∠-120°\)表示幅值\(V_p\)、滞后参考相位120°;\(V_p∠+120°\)表示幅值\(V_p\)、超前参考相位120°.
相量法:
例如,电压\(v(t)=V_pcos(ωt-120°)\)的相量形式\(V_{BN}=V_p∠-120°\)
线电压(Line-to-Line Voltage)指电机任意两相绕组之间的电压,即输入端之间的电压(如A-B、B-C、C-A).
例如:A相与B相之间电压\(V_{AB}\)
两相之间电压:
\(V_{AB}=V_{AN}-V_{BN}\)
- 平行四边形法则
设矢量\(\overrightarrow{A}\)(\(V_{AN}=V_p∠0°\)),矢量\(\overrightarrow{B}\)(\(V_{BN}=V_p∠-120°\)). 以\(\overrightarrow{A}, \overrightarrow{B}\)为邻边,画一个平行四边形,那么,平行四边形对角线矢量:
其中,
注意:复数\(c=a+ib\)(\(i\)是虚数单位),模长\(|c|=\sqrt {a^2+b^2}\)
最大线电压\(V_{line}\)为什么等于\(\sqrt 3\)最大相电压\(V_{p}\)?
以线电压\(V_{AB}\)为例,再由欧拉定理\(e^{jα}=cosα+jsinα\),知,
以\(V_{AN}=V_p∠0°,-V_{BN}=V_p∠60°\)为邻边,构造平行四边形,可得对角线
而\(V_p\)就是相电压\(V_{AN},V_{BN},V_{CN}\)最大值(幅值)
∴\(V_{line}=\sqrt 3V_{p}\)
电流环、速度环
- 电流环
电流环,矢量控制的最内环,通过采集相电流,与给定值比较,送入PI控制器,从而控制转矩.
电流环响应最快,频率一般20kHz. 电流环PI控制参数可根据公式计算,不过实际开发依然需要手动调试.
常用电流环参数估算方法:
其中,
其中,\(R_{s}\)相电阻,\(L_s\)相电感;\(K_{PDIV}\)比例系数的分数因子,使用时可灵活配置,如\(K_p=0.5\)时,为方便运算、提高分辨率,可令\(K_p=1024,K_{PDIV}=2048\);T电流环执行时间;\(ω_c\)电流环带宽;\(V_{busDC}\)直流母线电压;\(R_{shunt}\)采样电阻;\(A_{op}\)放大倍数.
\(i_d=0\)时,电流环控制就是q轴电流控制.
- 速度环
速度环,作为电流环输入,通过检测或估算的速度进行比较,将结果送到速度PI控制器,以输出电流给电流环.
速度环的调整频率一般小于电流环,常见速度环调整频率210kHz(周期0.5ms0.1ms);
速度环的检测频率必须大于其执行频率,否则速度环的调整无效,造成系统振荡.
SVPWM基础
基础矢量、矢量圆
SVPWM(Space Vector Pulse Width Modulation,空间矢量脉宽调制),通过三相逆变器的6个功率管输出随时间变化的PWM波,模拟三相对称正弦电流形成的电压矢量圆,产生接近圆形的磁链轨迹.
SVPWM利用平均值等效原理,在一个开关周期内,对基础矢量加以组合,产生与期望电压矢量相同的效果. 根据电压矢量的不同判断其所在的扇区区间,并利用相应扇区的基础矢量,不断合成所需要的电压矢量. 这样,电压矢量转动一圈,在空间上形成一个旋转的近似圆形磁场.
下图是典型的三相逆变器驱动电路:
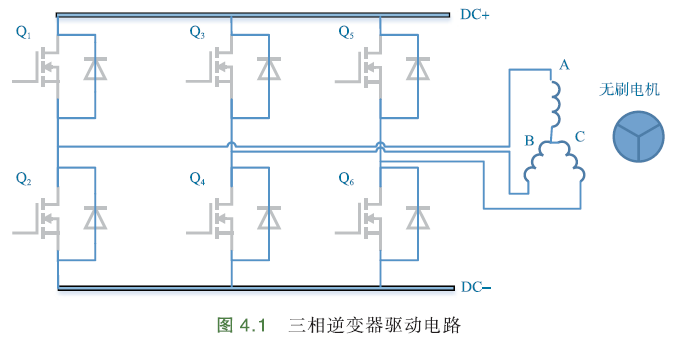
Q1~Q6是三相逆变器的6个功率管. 同一时刻,同一桥臂上下2个功率管不能同时导通,否则会造成电源短路.
所以,互补PWM波形中需要加入死区,防止短路造成危害.
因为上下2个功率管互补,所有可使用上桥臂功率管的状态表示该桥臂对应那一相的状态. 当上桥臂导通后,对应那一相与电源+ 连接;如果下桥臂导通,则该相直接与电源- 连接,电流从电机的端线流出.
设上桥臂导通、下桥臂关断,该桥臂状态记为1,反之记为0. 因为有3个桥臂,因此可定义开关函数\(S_x(x=a,b,c)\):
3个桥臂\(2^3=8\)种状态,即A、B、C三相8种状态组合.
假设一种状态组合:\(S_a=1,S_b=0,S_c=0\)(\(S_x=100\)),等效电路如下:
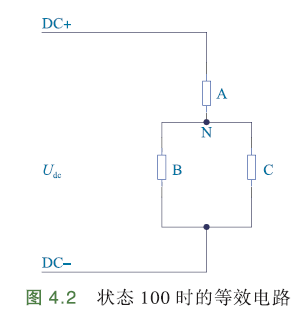
用\(U_a,U_b,U_c\)表示各相的相电压,即各相相对于电机中性点N的电压:
此状态下,B、C相相当于并联后,再与A相串联. 可得:
代入三相对称正弦电压矢量合成公式(等幅值):
系数\(2/3\)是为了确保变换前后幅值不变,又由欧拉公式\(e^{jx}=cosx+jsinx\),可得
同理,可求出其他开关状态下的相电压、合成矢量大小和方向,如下表:
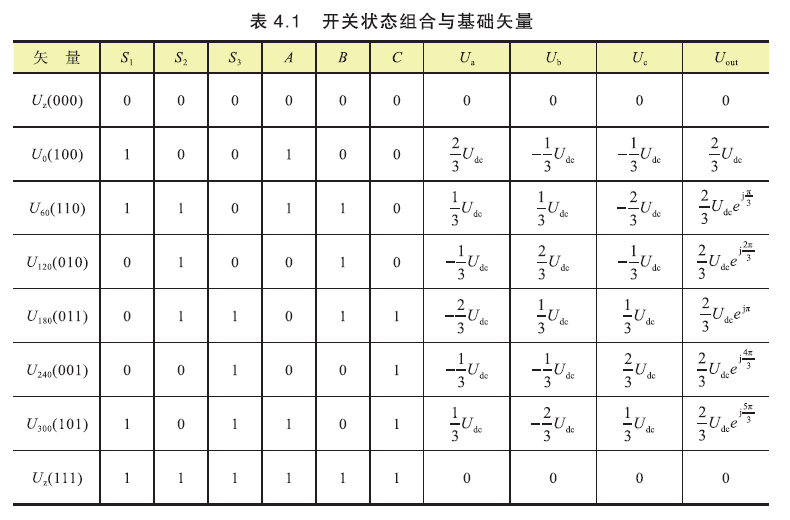
合成矢量可表示为\(U_{out}=\frac{2}{3}U_{dc}e^{jωt},ω=2πf\);6个基础矢量模长等值,均为\(\frac{2}{3}U_{dc}\)
将上面8个矢量(对应8种状态)放到矢量分布图中,如下图,红色为A-B-C三相空间静止坐标系.
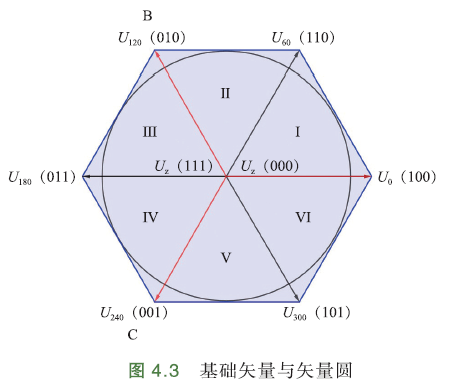
\(U_0(100)\)表示A相上桥臂导通,下桥臂关断;B、C下桥臂导通,上桥臂关断. 此时,起作用的是A相,该矢量与A轴重合. \(U_0(100)\)下标“0”,表示在矢量圆中的位置为0°;
\(U_{120}(010)\)表示B相上桥臂导通,A、C下桥臂导通. 此时,起作用的是B相,该矢量与B轴重合,空间上与\(U_0(100)\)相差120°,下标“120”表示在矢量圆中位置120°;
\(U_{60}(110)\)可看做相邻矢量\(U_0(100),U_{120}(010)\)的合成矢量;
\(U_{z}(111),U_z(000)\)是零矢量,不产生磁场,对电机不起作用.
这里的矢量\(U_z(000),U_0(100),U_{60}(110),U_{120}(010),U_{180}(011),U_{240}(001),U_{300}(101),U_z(111)\),就称为基础矢量. 每个基础矢量,对应功率管的一种开关状态.
如何求非零矢量\(U_{ref}\)在一段时间内产生的效果?
答:一个开关周期内某个矢量的作用效果 = 与它相邻的2个基础矢量分别作用不同时间的效果之和.
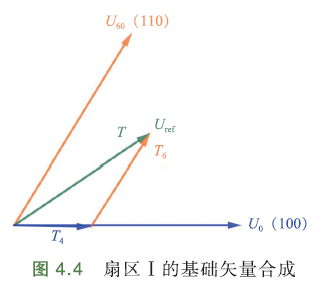
假设\(U_{ref}\)位于下图所示矢量图的扇区Ⅰ中,\(T_4\)是基础矢量\(U_0(100)\)的作用时间,\(T_6\)是基础矢量\(U_{60}(110)\)的作业时间. 设开关周期T,那么,
推广到全空间矢量,
其中,\(U_z\)零矢量,\(T_z\)零矢量作用时间,\(U_x,U_y\)某一扇区中2个相邻矢量,\(T_x,T_y\)是它们作用时间,\(T\)是\(U_{ref}\)作用时间.
因此,在一个扇区时间内,只要控制相邻矢量的作用时间(对应桥臂的导通时间),可合成平面圆内任意的非零电压矢量.
判断矢量所处扇区
如何确定合成矢量所处扇区(\(Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,or\space Ⅵ\))?
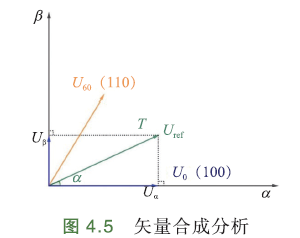
先假设由基础矢量\(U_0(100),U_{60}(110)\)合成矢量\(U_{ref}\)位于扇区Ⅰ,再看有什么特征. 将\(U_{ref}\)分解到αβ轴,得到\(U_α,U_β\). 有\(U_{ref}=U_α+U_β\)
\(U_{ref}\)位于扇区Ⅰ,有\(0<arctan(\frac{U_β}{U_α})<\frac{π}{3}\)
\(\iff U_α>0, U_β>0, \frac{U_β}{U_α}<\sqrt 3\)
同理,可推导出合成矢量落在其他扇区的充要条件:

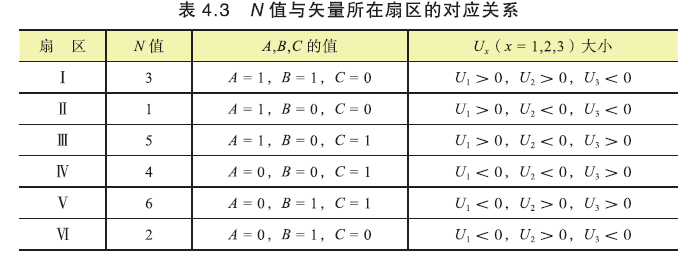
∴合成矢量所在扇区由\(U_α,U_β,\sqrt 3U_α - U_β, -(\sqrt 3U_α + U_β)\)的符号决定.
为简化运算,可定义:
且满足\(U_1+U_2+U_3=0\)
继续简化计算,规定:
如果\(U_1>0,A=1\),否则\(A=0\);
如果\(U_2>0,B=1\),否则\(B=0\);
如果\(U_3>0,C=1\),否则\(C=0\);
不存在\(A,B,C\)全为0或1的情况.
注意:这里A、B、C只是一个符号,不是指三相.
令\(N=A+2B+4C\),通过不同A、B、C组合得到N值,能很方便判断出所处扇区.
矢量作用时间分析
如何确定合成矢量相邻的2个基础矢量的作用时间?
假设矢量角速度\(ω=2πf_0\),\(f_0\)旋转电压频率,即正弦电压矢量的频率,周期\(T_0=\frac{1}{f_0}\).
设载波频率\(f_s\)(即PWM频率),那么频率比\(R=\frac{f_s}{f_0}\). 将平面圆均分为R份,每份角度递增:
设载波周期T(PWM周期),\(T=\frac{1}{f_s}\),
∴
当合成矢量走过整个圆后,会在空间上形成旋转的电压矢量,从而形成一个近似圆形的旋转磁场.
如下图,假设合成扇区Ⅰ的某个非零矢量\(U_{ref}\). \(T_4\) 是基础矢量\(U_0(100)\)作用时间,\(T_6\) 是基础矢量\(U_{60}(110)\)作用时间,\(T\) 是(功率管)开关周期(PWM周期),\(T_0,T_7\)分别是零矢量\(U_z(000),U_z(111)\)作用时间.
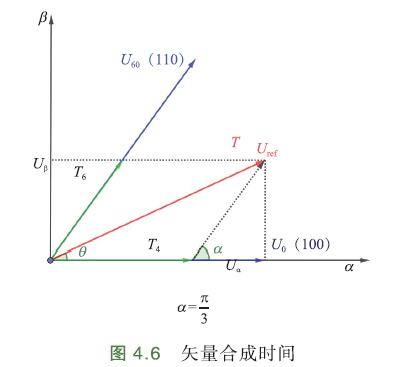
非零矢量\(U_{ref}\)与α轴夹角θ(即电角度). 由正弦定理:\(△\)三条边分别与其相对角度正弦值的比值是个固定值,该比值就是三角形外接圆的直径:
∵基础矢量模长\(\frac{2}{3}U_{dc}\)
∴\(|U_0(100)|=|U_{60}(110)|=\frac{2}{3}U_{dc}\)
∴
2个零矢量作用时间\(T_0=T_7=\frac{T-T_4-T_6}{2}\)
定义\(m=\sqrt 3\frac{|U_{ref}|}{U_{dc}}\)为SVPWM的调制系数
当\(θ=\frac{π}{6}\)时,\(T_4+T_6=T\),输出矢量最大幅值\(|U_{ref}|=\frac{1}{\sqrt 3}\frac{T_6}{Tsinθ}U_{dc}=\frac{\sqrt 3}{3}U_{dc}\)
∴可输出最大相电压(相电压幅值)\(V_p=\frac{\sqrt3}{3}U_{dc}\)
∵变换过程幅值不变
∴\(|U_{ref}|=V_p\)
∴最大线电压\(V_{line}=\sqrt 3 V_p=U_{dc}\)
传统SPWM(正弦脉宽调制)线电压最大\(\frac{\sqrt 3}{2}U_{dc}\),而SVPWM(空间矢量脉宽调制)线电压最大\(U_{dc}\),因此,SVPWM直流母线利用率提高15.47%:
由上面\(T_4,T_6\)计算公式知,要计算基础矢量作用时间,需要计算三角函数值. 而普通MCU没有浮点数计算能力,计算三角函数常需要通过查表实现.
能否不使用三角函数,只通过简单加减逻辑运算确定基础矢量的作用时间?
答案是可以的. 以扇区Ⅰ为例,将合成矢量\(U_{ref}\)分别投影到α、β轴,那么,

合成矢量\(U_{ref}\)在αβ轴投影,可以分解为\(U_0(100),U_{60}(110)\)分别在αβ轴投影,然后再求它们的和.
基础矢量\(U_0(100)\)作用时间\(T_4\),全部分量在α轴;基础矢量\(U_{60}(110)\)作业时间\(T_6\),在α轴投影\(U_{60}(110)cos\frac{π}{3}T_6\),在β轴投影\(U_{60}(110)sin\frac{π}{3}T_6\)
∴
矩阵形式:
整理得,
∴
上一节中,为了方便判断合成矢量所在扇区,我们定义了:
设\(K=\frac{\sqrt 3}{U_{dc}}T\),扇区Ⅰ基础矢量的作用时间可写成:
不难发现,表现形式更简洁. \(T_0,T_4,T_6\) 不用三角函数计算,也消掉了\(θ\).
同理,可推导出合成矢量在其他扇区时,基础矢量的作用时间.
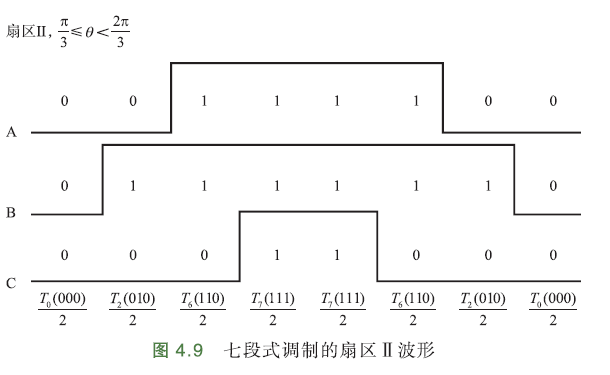
扇区Ⅱ:
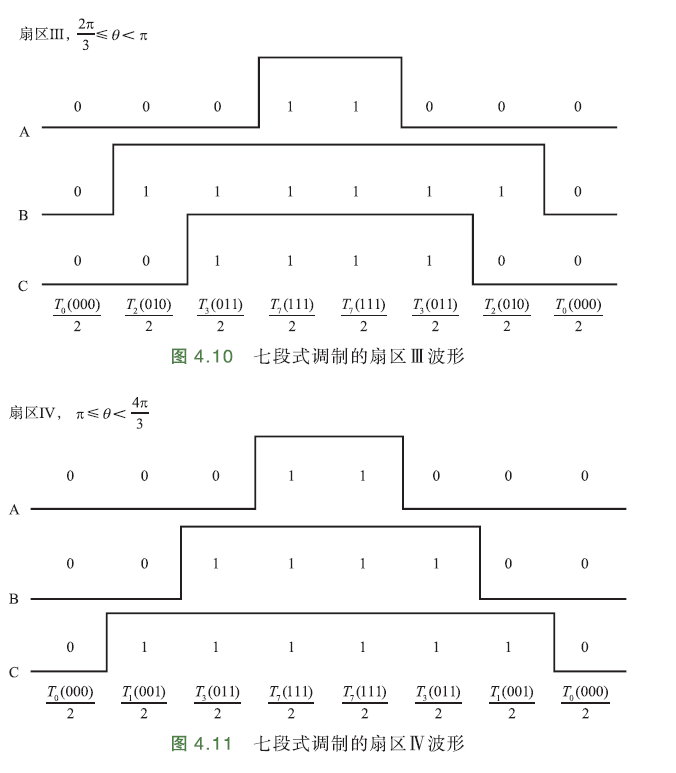
扇区Ⅲ:
扇区Ⅳ:
扇区Ⅴ:
扇区Ⅵ:
当2个零矢量作用时间为0时,即\(T_0=T_7=0\),非零矢量作用时间最长,此时合成矢量幅值最大.
如下图,合成矢量的最大幅值不超过6个基础矢量所决定的圆形区域:
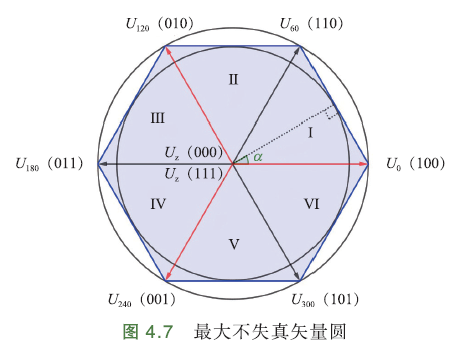
SVPWM能输出的最大不失真电压矢量是正六边形的内切圆,半径:
这就是逆变器输出的最大不失真相电压的幅值.
当合成矢量落在正六边形与外切圆之间区域时,将会发生过调制,此时可采用等比例缩小的措施.
七段式调制方式分析
现在确定了合成矢量所需基础矢量的作用时间,但怎样将MCU、PWM结合起来呢?
下面讨论该问题.
为了减小谐波,得到更好效果,一般采用以下脉宽调制原则:
1)每次矢量变化,只改变一个桥臂上的一组功率管;
2)合理利用零矢量,尽可能减少功率管的开关次数,减小功率管通断过程造成的损耗;
3)尽可能减小系统谐波分量,特别低频信号的谐波分量;
4)优化矢量合成算法,减少CPU处理时间.
有两种常用PWM方式:
1)对称式调制,即七段式调制;
2)低开关损耗,即五段式调制.
七段式调制的开关次数比五段式多些,但波形对称,谐波分量小,目前应用较多.
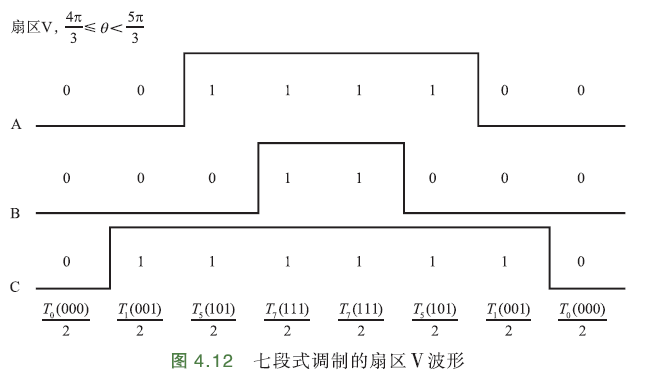
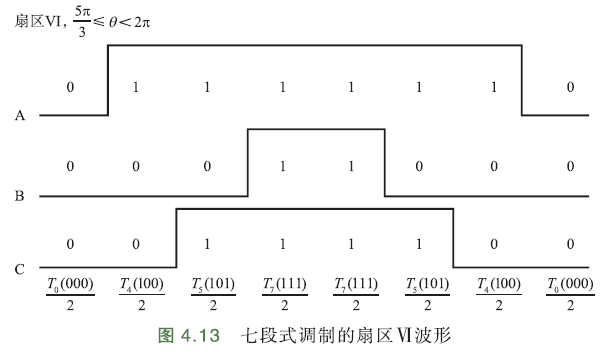
七段式调制的PWM三相波形呈对称分布,一个周期由七段组成,共需要6次开关切换,每次开关状态转换只改变其中一组开关状态. \(U_z(000)\) 零矢量放在两边,左右对称,中间零矢量\(U_z(111)\),可有效减小PWM谐波分量.
当\(U_0(100)\)切换到零矢量\(U_z(000)\)时,只需要改变A相上下桥臂的功率管状态;
当\(U_0(100)\)切换到零矢量\(U_z(111)\)时,需要改变B、C相功率管状态,因此需要合理分配\(U_0(100)、U_z(000)、U_z(111)\)的作用时间,确保每次只切换一组功率管的状态,尽可能减少功率管的切换次数,减少系统谐波分量.
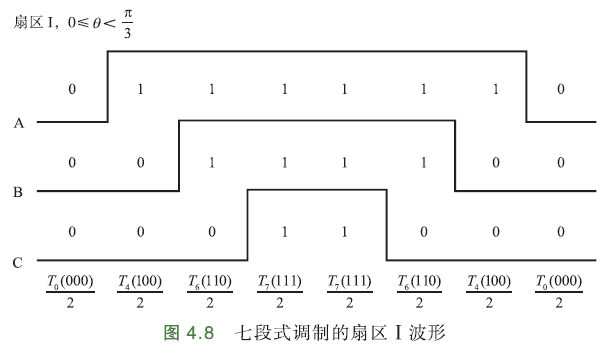
例如,扇区Ⅰ中合成矢量由2个基础矢量\(U_0(100),U_{60}(110)\)组成,根据上面开关切换原则,配合零矢量,且每次只改变一组开关,那么扇区Ⅰ的开关切换顺序:
且只有这一种切换顺序. 中间零矢量\(U_z(111)\)有2个作用时间,且不需要切换,一共7段波形,6次切换.
由此可推断出七段式调制的扇区波形:
PWM占空比计算
确定了PWM方式,如何计算PWM占空比呢?
这是SVPWM最后一步,也是最关键一步.
如下图,采用PWM模式2下的中心对齐模式,即 计数器TIM_CNT < CCR时,输出低电平,反之输出高电平
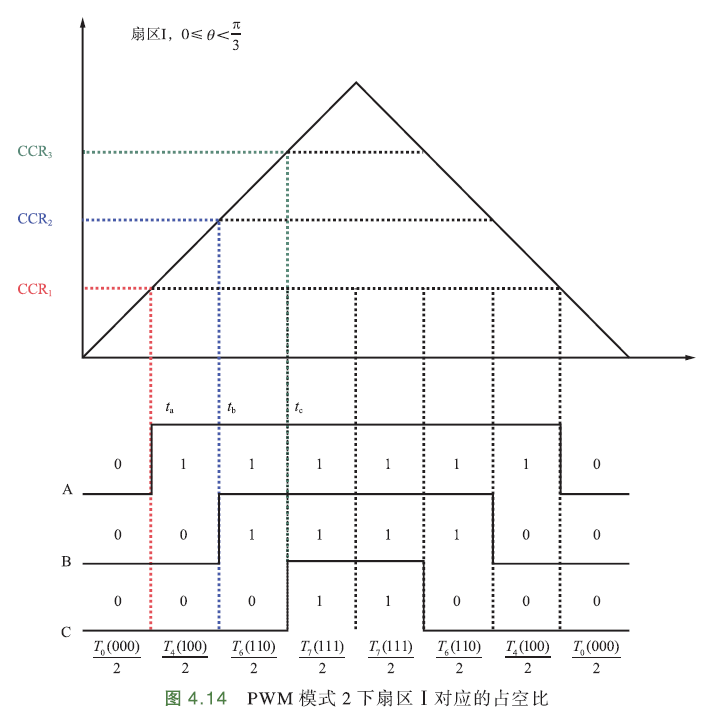
从扇区Ⅰ可推出,比较器A先到给定值,B次之,最后是C. 三路比较器都是对称发波.
假设\(T_x,T_y\)分别表示先作用、后作用的有效基础矢量的作用时间,那么\(T_x\)表示扇区Ⅰ中的基础矢量\(U_0(100)\)的作用时间\(T_4(100)\),\(T_y\)表示\(U_{60}(110)\)的作用时间\(T_6(110)\). \(T_0(000)\)表示零矢量\(U_z(000)\)作用时间,\(T_7(111)\)表示零矢量\(U_z(111)\)作用时间.
如上图,CCR1值对应\(\frac{T_0(000)}{2}\),CCR2值对应CCR1值加上\(\frac{T_4(100)}{2}\),CCR3值对应CCR2加上\(\frac{T_6(110)}{2}\)
∴
其中,
- \(t_a\) 表示先作用电压矢量的开始作用时刻,因为一个周期有2个零矢量(\(T_0,T_7\)),且都左右对称,所以\(T_a\)右侧除以4
- \(t_b\)次作用电压矢量的开始作用时刻;
- \(t_c\)零矢量\(U_z(111)\)开始作用时刻.
- \(T_x,T_y\)分别是先后作用的2个基础矢量的作用时间(前面矢量作用时间分析已求出,不同扇区下对应不同的时间值).
- \(T_a,T_b,T_c\)表示三路占空比,\(t_a,t_b,t_c\)也代表了各自\(CCR_x\)值.
这样,就能推算出其他扇区对应的比较器的值. \(CCR_A,CCR_B,CCR_C\)表示的三路比较器的值,如下表:
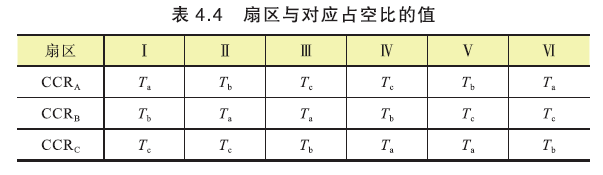
如果是PWM模式1,即当TIM_CNT < CCR时,输出高电平;大于CCR且小于最大值ARR时,输出低电平,那么对应占空比如下图:
基础矢量开始作用的时刻计算方式不变,计算占空比时注意一下方向.
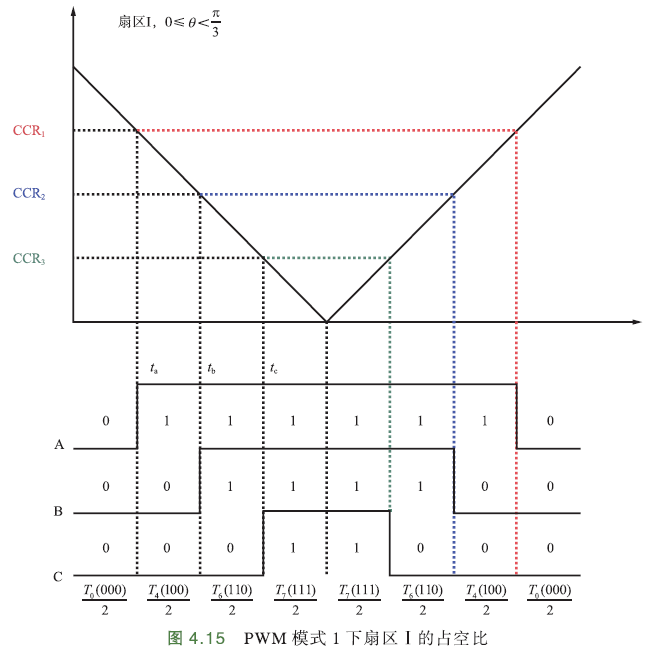
矢量开通的先后时间未变,\(t_a、t_b\)表示先作用矢量、后作用矢量的开始作用时刻;\(t_c\)零矢量\(U_z(111)\)开始作用时刻. \(T_x、 T_y\)表示先作用基础矢量、后作用基础矢量的作用时间.
CCR1对应值\(\frac{T_7(111)}{2}+\frac{T_6(110)}{2}+\frac{T_4(100)}{2}\),CCR2对应值\(\frac{T_7(111)}{2}+\frac{T_6(110)}{2}\),CCR3对应值\(\frac{T_7(111)}{2}\)
由前面计算知,零矢量作用时间\(\frac{T-T_x-T_y}{4}\),那么CCR1对应值\(\frac{T-T_x-T_y}{4}+\frac{T_y}{2}+\frac{T_x}{2}=\frac{T+T_x+T_y}{4}\);
CCR2值与CCR1值差一个基础矢量\(U_0(100)\)作用时间的一半,即\(\frac{T_4(100)}{2}=\frac{T_x}{2}\);
CCR3值比CCR2的值差一个基础矢量\(U_{60}(110)\)的作用时间的一半,即\(\frac{T_6(110)}{2}=\frac{T_y}{2}\)
∴PWM模式1下占空比计算公式:
其中,\(T_x,T_y\)分别是当前扇区先作用基础矢量、后作用基础矢量的作用时间.
逆变器死区效应及其补偿
为什么插入死区
为什么需要死区?
SVPWM采用逆变器方式,通过MOSFET或IGBT的开关模式组合,产生相应的空间电压矢量,以逼近三相对称正弦电流所产生的基准圆形磁动势.
因为电荷存储效应,功率管开关存在一定的延时,特别关断时间 > 导通时间. 如果关断过程中,另一个截止的功率管立即导通,相当于电源正负极短路,需要避免.
如下图,蓝色波形:功率管理想输入波形;绿色波形:功率管实际导通波形;红色区域:同一桥臂上下开关同时导通的风险区域.
为了避免同一桥臂的2个功率管不发生直通现象(电源短路),必须在导通和关断信号之间插入死区.
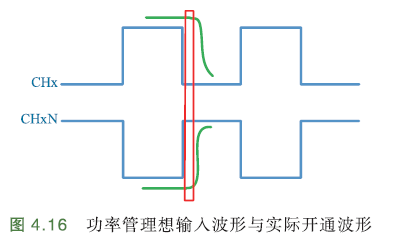
死区是什么?
在死区时间内,桥臂上下都处于截止状态. 没有触发信号,桥臂的状态将取决于功率管反向并联的2个续流二极管及电流方向.
如何确定死区时间?
可通过测试功率管的通断延时来确定. 考虑到外界干扰以及一些寄生参数的影响,设置死区时必须设置一定的裕量:比如功率管通断延时500ns,那么可设置800ns或以上死区时间.
注意:死区时间不宜过长,否则会缩小占空比调节范围,降低系统动态性能.
插入死区后,PWM波形如下图:
插入死区后,同一桥臂上下管存在同时关闭的情况,尽管单个周期引起的电压误差很小,但由于开关频率较高,死区引起误差的叠加不可忽视,容易引起电机输出电压基波分量的减小.
再加上功率管本身的通断延时,理想的调制信号和功率管实际输出信号之间存在一定偏差,容易导致输出电压波形畸变,基波幅值减小,谐波分量增大,电机产生转矩脉动,从而进一步影响系统性能.
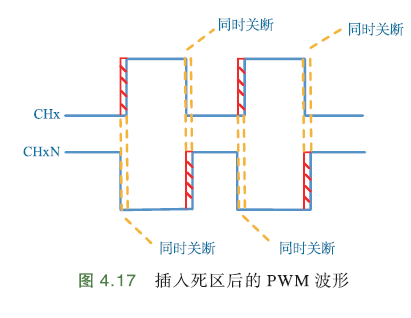
转矩脉动:理想情况下,电机应输出恒定转矩(如直流电机或理想永磁同步电机);但实际上,由于电磁、机械或控制等因素,转矩会围绕平均值周期性波动,这种现象称为转矩脉动.
在低速及小负载情况下,常发生零电流钳位的现象,导致输出电流波形畸变,动态性能下降.
死区效应分析
实际死区时间\(T_D受功率管的通断时间、功率管压降、续流二极管压降的同时影响,要计入时间常数\)T_e\(,即\)T_D=T_d-T_e\(. 为简单考虑,下面分析忽略\)T_e$
下图是典型的三相逆变器驱动电路:
Q1~Q6是6个功率管,每个功率管都反向并联一个续流二极管. DC+为电源+,O为电源-,A、B、C为电机的三相输入端,N为中性点. a,b,c表示3个桥臂中点,分别连接电机的3个输入端.
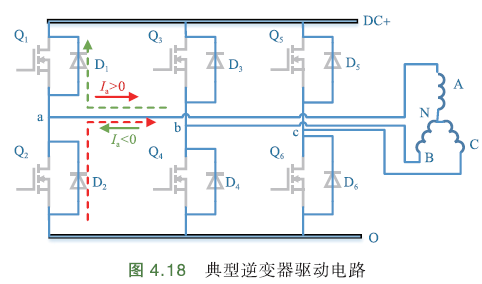
以A相为例,功率管开关时,由于死区存在,逆变器的输出电压根据电流的极性不同而不同.
假设电流正向:电机端->中性点.
当\(I_a>0\)时,有两种工作状态:
1)正常状态:Q1导通,Q2关断,电流方向为正. 如果忽略功率管压降,那么\(u_{ao}=U_{dc}\);
2)死区状态:上下管同时关断. 此时,电机为感性负载,电流不能突变,通过与Q2反向并联的续流二极管\(D_2\)续流. 如果忽略Q1压降,那么\(u_{ao}=0\).
正常情况下,\(u_{ao}=u_{dc}\),因为死区存在,上管损失\(\frac{T_d}{T_s}U_{dc}\)的平均电压作用量. \(T_s\)是PWM周期,\(T_d\)是死区时间;
当\(I_a<0\)时,有两种工作状态:
1)正常状态:Q1关断,Q2导通,电流方向为负:从线A流入逆变器,并从Q2流入电源负极. 如果忽略Q2压降,那么\(u_{ao}=0\);
2)死区状态:上下管同时关断. 此时,电机为感性负载,电流不能突变,通过与Q1反向并联的续流二极管\(D_1\)续流. 如果忽略\(D_1\)压降,那么\(u_{ao}=U_{dc}\).
同理,正常情况下,\(u_{ao}=0\),因为死区存在,多出\(\frac{T_d}{T_s}U_{dc}\)的平均电压作用量.
下图:
(a)(b)理想输出占空比波形,上下对称发波,无死区;
(c)(d)为避免同一桥臂上下管同时导通,加入死区时间后的PWM波形;
(e)\(U_{ao}\)的理想输出电压波形,幅值\(U_{dc}\),即电源电压;
(f)A相\(I_a>0\)时的\(U_{ao}\)实际输出波形,比\(U_{ao}\)的理想波形少了死区时间;
(g)A相\(I_a<0\)时的\(U_{ao}\)实际输出波形,比\(U_{ao}\)的理想波形多了死区时间;
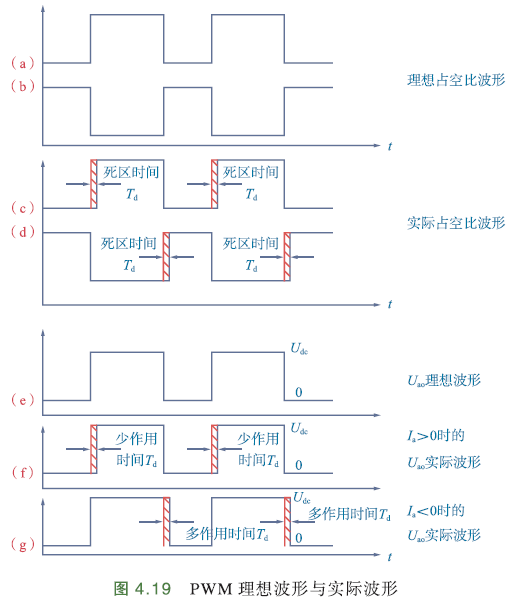
死区存在,会导致系统输出电压出现偏差,功率管开关频率越高,死区累积效应越明显. 为减小死区效应,需要对PWM波形进行补偿.
死区补偿方法
死区补偿有两种方法:1)硬件补偿法;2)软件补偿法.
硬件补偿
硬件补偿分为:电压反馈补偿,电流反馈补偿.
- 电压反馈补偿:先测量逆变器的实际输出电压,之后与目标输出电压进行比较,将差值作为补偿量叠加到期望输出电压指令上,作为新的输出.
优点:该方法闭环控制,能有效消除实际电压与目标电压的差值,对负载电流变化不敏感,补偿效果较好.
缺点:补偿电路结构复杂,算法复杂,成本增加,应用较少.
- 电流反馈补偿:利用偏差方波电压与电流极性的关系,通过检测三相电流的极性,得到合适的补偿电压.
优点:常用无刷直流电机都具备电流检测电路,硬件无需额外电路,结构简单.
缺点:需要无误差电流反馈,且要求没有信号滞后情况. 实际电流检测中,常需要滤除电流中高频分量,滤波常引起信号滞后,补偿效果受电流检测精度影响很大,且需要精确检测电流过零点,不容易实现.
软件补偿
软件补偿原理:在控制程序中加入死区补偿算法. 常见算法:电压输出时间补偿、旋转坐标补偿、预测电流控制补偿、基于脉冲的死区补偿等.
- 电压输出时间补偿:以瞬时平均电压为基础,每个PWM载波周期对输出电压的平均进行补偿,出现偏差时加入死区补偿,使输出电压逼近理想输出电压.
该方法需要检测电流过零点,当系统干扰较大或电流成分中高次谐波较大时,往往存在误判现象.
过零点: 指交流信号(电压或电流)在周期性变化过程中,从正半周过渡到负半周(或反向)时经过零值的瞬间.
- 旋转坐标补偿:将给定电流值\(i_q,i_d\)作为参考电流,通过Park反变换得到两相静止坐标系下的\(i_α,i_β\)后,再经过Clarke反变换得到三相静止坐标系下的\(i_a,i_b,i_c\),最后根据每相电流的极性计算出每相电压的补偿极性,补偿电压幅值就是误差电压的平均值. 得到每相补偿电压后,在经过Clarke、Park变换,得到两相旋转坐标系下的\(Δv_q,Δ_d\),作为电压补偿量,进行补偿.
该方法计算繁琐、计算量大,实际很少使用.
- 预测电流控制补偿:类似于卡尔曼滤波的预测控制,运用预测控制理论,根据k时刻采集到的负载电流以及补偿输出的电流,运用直流无刷电机的数学模型计算k+1时刻的目标电流值,并计算出符合电流变化的输出电压矢量. 之后利用前面提到的矢量合成方法,合成该电压矢量,并进行输出,调节下一次采样时的实际电流值,从而实现电流跟踪的目的.
该方法实现不容易.
- 基于脉冲的死区补偿:通过调整PWM实际发波脉冲,达到修正给定电压与实际输出电压之间偏差的目的. 在脉冲产生畸变之前,对该相加入死区补偿时间,使补偿后的PWM脉冲在相位和宽度上更接近理想脉冲.
该方法精确性较高,能使逆变器的输出电压在相位和幅值上基本无误差,不受系统的工作频率、载波频率、负载的限制,只与电流极性相关,算法简单,容易实现,应用较多.
当\(I_a>0\)时,由于死区存在,电压输出少一个死区作用时间,补偿方法是将上桥臂的理想开通时间延长\(T_d\). 考虑互补作用,相应下桥臂作用时间缩短\(T_d\),保证实际开通波形与理想输入波形一致;
当\(I_a<0\)时,由于死区存在,电压输出多一个死区作用时间,补偿方法是将上桥臂理想开通时间缩短\(T_d\). 考虑互补作用,相应下桥臂开通时间延长\(T_d\).
所谓互补,是指桥臂对应功率管互补调节. 如某个扇区内,Q3、Q4、为一组互补输出,Q5、Q6为一组互补输出,Q1、Q2为关断. 好处:上管关断瞬间电流可由下管续流,下管关断时瞬间电流可由上管续流,而不经过功率管内部续流二极管(经过外部并联的),从而避免大电流损害功率管.
什么是互补PWM?
一对互补PWM输出如下图:
from https://blog.csdn.net/qq_20222919/article/details/106466415
电流极性判断
电流极性判断指判断电流方向,它是正确进行脉宽电压补偿的前提.
可行方法:
1)通过电流过零点的计算,来判断电流的方向
2)通过坐标反变换获得三相静止坐标系下的各相电流
3)高效方法(推荐):
首先,坐标变换后得到d-q两相旋转坐标系下的\(i_d,i_q\)后,根据它们关系算出电流合成矢量所处位置
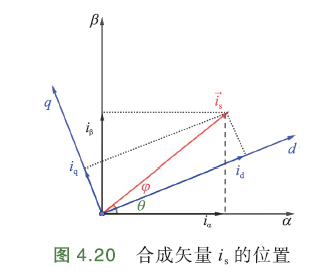
角度\(φ\)是电流合成矢量\(i_s\)与旋转坐标系d轴的夹角,\(tanφ=\frac{i_q}{i_d}\to φ=arctan\frac{i_q}{i_d}\). \(θ\)是d轴与α轴夹角(α轴与A轴重合),是磁场位置角,即电角度,随时间变化. 合成矢量\(i_s\)与α轴夹角\(δ=φ+θ\)
得到电流合成矢量的空间角度\(δ\)后,可根据空间角度找到对应电流的极性.
为此,设计一个矢量圆,如下图. 红线表示A、B、C三相电压矢量的正端方向,它们各自的反方向为各种的负端方向. 如\(a_1a_2⊥A\)相线段,那么\(a_1a_2\)右侧是A相的正端方向,该区域的A相电流为正;左侧是A相的负端反向,该区域的A相电流为负.
线段\(a_1a_2\)为A相的零点换向时刻. A+表示A相电流为正方向,A-表示A相电流为负方向.
同理,可以得到B+,B-,C+,C-电流方向分布图.
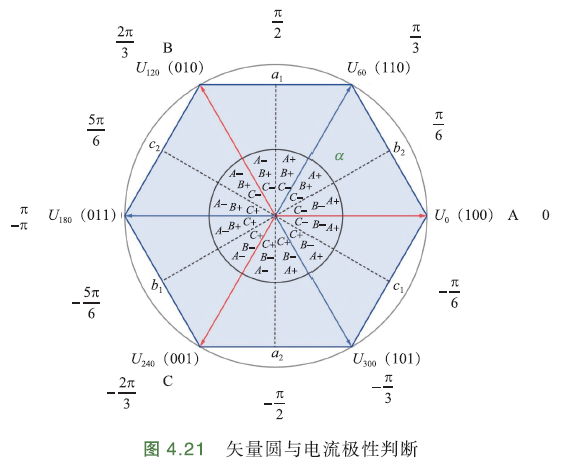
于是,我们将三相电流的分布组合到一起,便可以推出电流极性与电流合成矢量角度\(δ\)的关系:
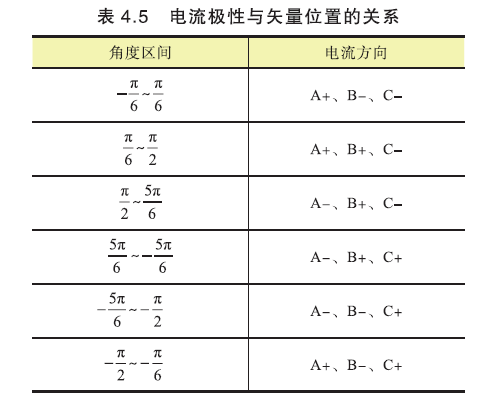
之后,根据电流方向,结合七段式调制的PWM波形,即可得到各区间A、B、C三相脉冲死区补偿时间.
- 扇区Ⅰ区间0~π/6的PWM补偿方案
以七段式调制扇区Ⅰ的PWM波形为例,区间0~π/6,A、B、C三相电流方向A+、B-、C-. 根据前面(死区补偿)分析,电流为正时,上桥臂功率管理想开通时间延长\(T_d\),电流为负时,上桥臂功率管理想开通时间缩短\(T_d\),那么可以推导出扇区Ⅰ的0~π/6区间死区补偿波形,如下图:
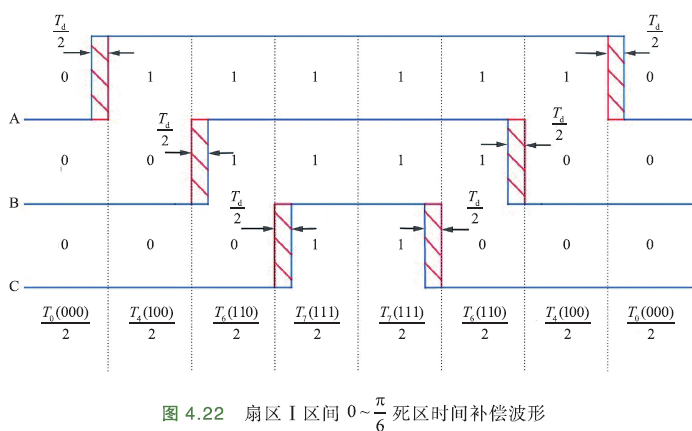
A、B、C对应三相逆变器上桥臂功率管的PWM波形输入,即互补通道的正端输入. 虚线表示未经补偿的波形变换时刻,红色区域为死区时间,蓝线为补偿后的实际PWM波形. 可看出,A相上桥臂左右各延长\(\frac{T_d}{2}\)作用时间,B、C相上桥臂左右各缩短\(\frac{T_d}{2}\)作用时间.
参考七段式调制PWM的发波时间,补偿后的计算方法:
其中,\(T_a,T_b,T_c\)为未补偿时的三相开通时刻;\(T_a',T_b',T_c'\)为补偿后的三相开通时刻.
三相补偿后,\(U_4(100)\)作用时间增加了\(2T_d\),\(U_6(110)\)作用时间未变,零矢量作用时间减少了\(2T_d\). 如果B、C相触发信号不变,单独将A相的死区作用时间延长\(2T_d\),也有同样效果,此时A相开通时刻:\(T_a'=T_a-T_d\)
- 扇区Ⅰ区间π/6~π/3的PWM补偿方案
此时电流方向A+、B+、C-,PWM波形位于扇区Ⅰ. A、B相电流应该延长一个\(T_d\)死区作用时间,C相缩短一个\(T_d\)死区作用时间. 如下图:
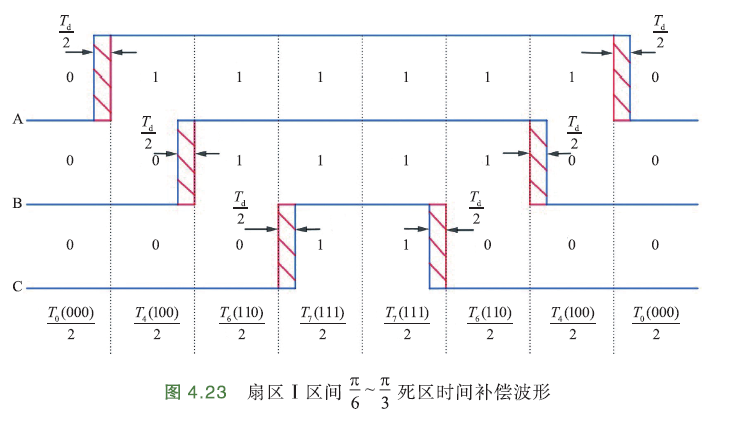
A相电流为正,所以左右各延长\(\frac{T_d}{2}\)死区作用时间. 虚线是未补偿时,波形切换时刻. 有:
矢量\(U_4(100)\)作用时间未变化,\(U_6(110)\)作用时间+\(2T_d\),零矢量作用时间-\(2T_d\).
同理,可推出其他区间PWM补偿方案.
相电流采集、重构
相电流采集方法:电流互感法,分流电阻法等.
-
双电流互感芯片电流采样:不受功率管开通的限制,任何时刻都能采集电流,抗干扰能力强,但成本高;
-
分流电阻采样:成本低、易用,应用较多. 可分为:单电阻法、双电阻法、三电阻法.
单电阻法
采样电阻设在三相下桥臂汇流点与电源地端之间. 只有一个采样电阻,三相电流的测量相同,只需要一个运算放大电路,不需要为每一相电路单独校准.
特点:硬件成本低,但算法稍复杂.
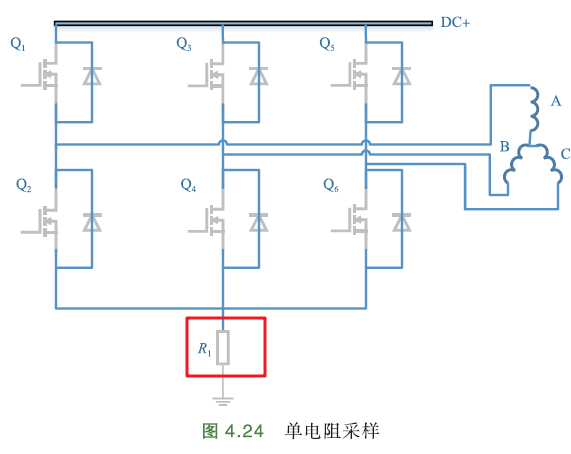
单电阻采样需要每个PWM周期采样2次,才能重构出三相电流. 以七段式调制扇区Ⅰ的PWM波形为例,分析如何重构三相电流:
- 第1次电流采样
如下图,红线对应A、B、C三相状态1、0、0,即A相上桥臂开通,下桥臂关断,A相直接连到电源+;B相上桥臂关断,下桥臂开通;C相上桥臂关断,下桥臂开通.
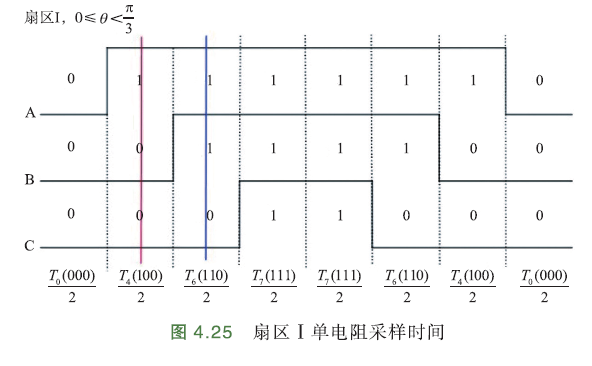
因为波形对称(中心对称),所以也可以在对称的一方采样.
A、B、C相状态为1、0、0时,电流由电源+流入A相,并从B相和C相流出,最后经采样电阻R1到电源-. 如下图:
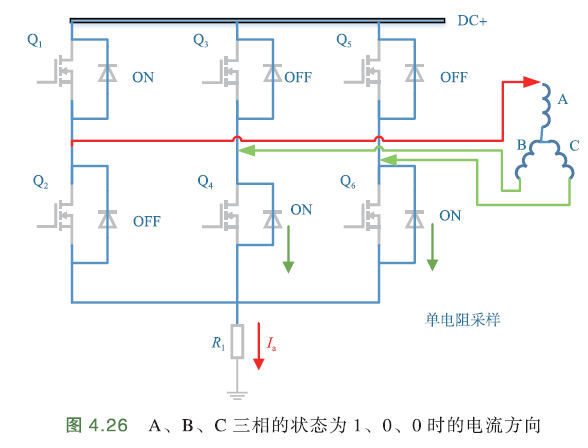
假设电流方向从逆变器流进电机的相线为正,反之(流出)为负,那么此时,流经R1的电流为\(I_a\). 为了得到三相电流,需要再采集一相,剩余一相可用基尔霍夫电流定律求出.
- 第2次电流采样
如下图,A、B、C三相状态1、1、0,A相上桥臂开通,下桥臂关断,A相接电源+;B相上桥臂开通,下桥臂关断,B相接电源+;C上桥臂关断,下桥臂开通. 电流:电源+ -> A相,B相 -> C相 -> R1 -> 电源-
∴流经R1的电流\(-I_c\)
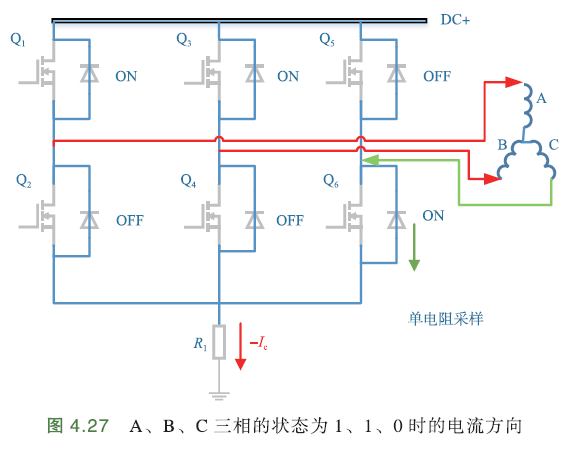
在一个PWM周期内2次电流采样后,再根据基尔霍夫电流定律,计算出第三相电流,才能完成一次电流重构.
特殊情况:当一个PWM周期内,两相占空比接近或相同时,其中一相采样窗口将变得很小,无法正确采样到该相电流,这样就无法重构出三相电流值. 此时,可对该周期的PWM占空比进行调整,增大采样窗口,以便于获取该相电流.
单电阻采样特点:程序复杂,只在电源地端设置一个检测电阻,必须在特定时刻采集相电流. 该方式检测到的电压只有正值,不需要相移电路,只需要一路运算放大器,成本低.
双电阻法
双电阻采样是在三相桥臂中的两相的下桥臂,分别串联一个采样电阻进行采样.
不同于单电阻法,双电阻法只需要在每个PWM周期采样一次即可重构出三相电流值.
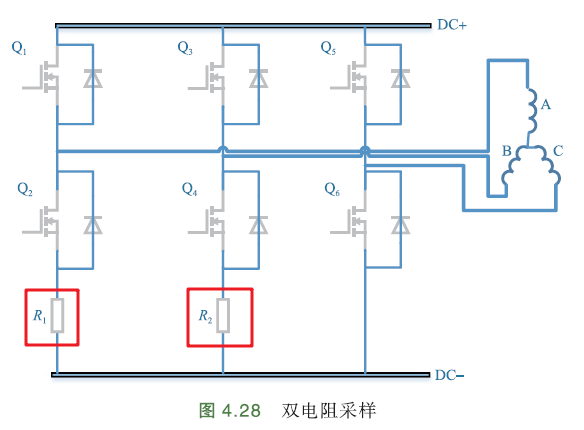
由于PWM对称发波方式,而且只在下桥臂开通情况下才能采集到有效的相电流,因此只需要在PWM的中心对称点,即零矢量的中心处采样.
如下图,只有2相下桥臂设置了采样电阻,采集2相电流.
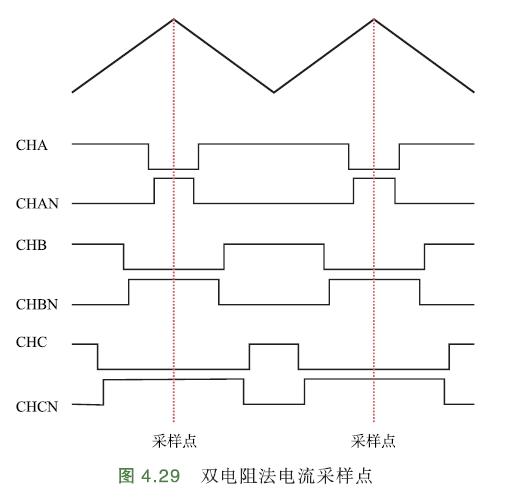
双电阻采样问题:当某一相的下桥臂开通时间很短时,该相的采样窗口会变得很小,可能造成采样电流不准确.
为了提高采样准确性,可以使用三电阻采样法.
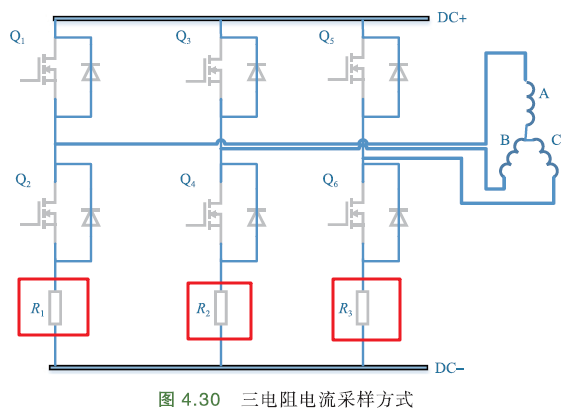
三电阻法
三电阻采样法是在每相桥臂的下端都设置一个采样电阻,在下桥臂开通时进行电流采样. 因为有3个电阻,所以理论上可以同时采集三相电流,但为了避免某一相下桥臂开通时间太短,采集窗口太窄而导致电流采样不准确,所以每次采样可以避开那一相,而采集另外两相.
简而言之,根据不同扇区的波形,分扇区采样.
如下图,A、B、C三相下桥臂分别设置一个采样电阻:
- 扇区Ⅰ、扇区Ⅵ
七段式调制PWM波形中,扇区Ⅰ、扇区Ⅵ的波形类似,都是A相上桥臂开通时间最长,下桥臂开通时间最短,如下图:
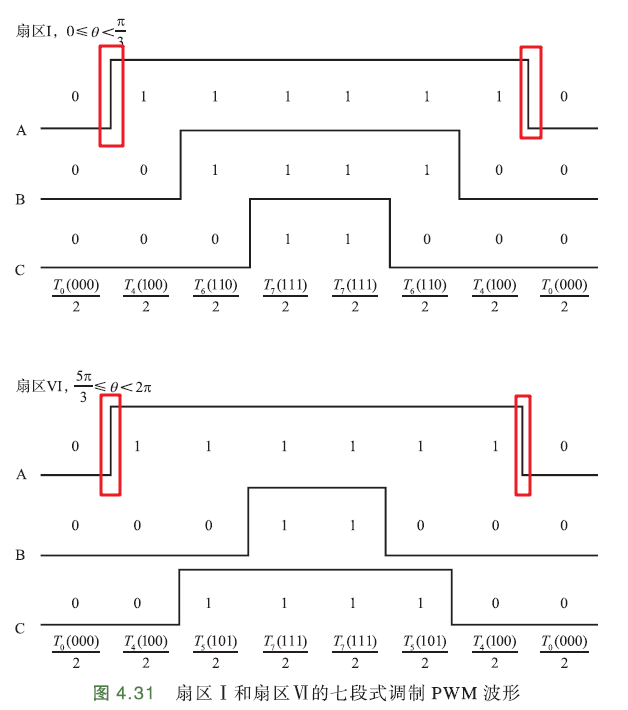
相电流只有在下桥臂开通时,才能有效采样,而扇区Ⅰ、扇区Ⅵ的A相下桥臂开通时间最短,所以此时可在三相下桥臂开通时只采集B相、C相电流. A相电流可由基尔霍夫电流定律求出.
下图解释了为什么不同时采集三相电流. 下图展示了三电阻采样下扇区Ⅰ、扇区Ⅵ的采样点,其中,CHA、CHB、CHC代表PWM高端输入,对应各相的上桥臂. 当上桥臂为低时,由于互补作用,对应下桥臂为高.
采样点需要在下桥臂开通时,即上桥臂关断时. 采样前一时刻,A相上桥臂为高时,A相直接与电源的正极接通;B相、C相上桥臂关断,下桥臂接通,电流由电源进入电机的A相,由B相、C相流出,并经过B相、C相上的采样电阻到电源-.
进入采样区域时,A相上桥臂关断,由于电感的作用(电机绕组),电流不会突变,电流方向也不会改变,电流由A相端线流入中性点. 此时,B相采样电阻、C相采样电阻上的电流流入地. 由于续流管D2(与Q2并联)的存在,电流会由电源- 流经A相采样电阻,并经过D2.
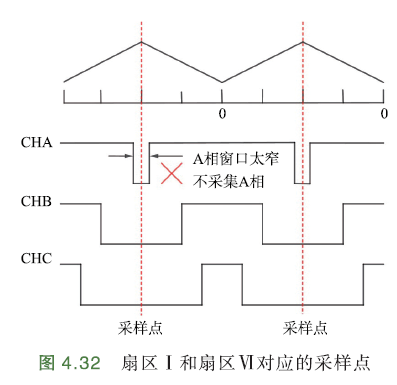
前面已经提过,假定电流从电机三相端线流向中性点方向为正,反之为负. 那么,在扇区Ⅰ、扇区Ⅵ的采样区域内,电流从A相流入,从B、C相流出,因此\(I_a\)为正,\(I_b,I_c\)为负.
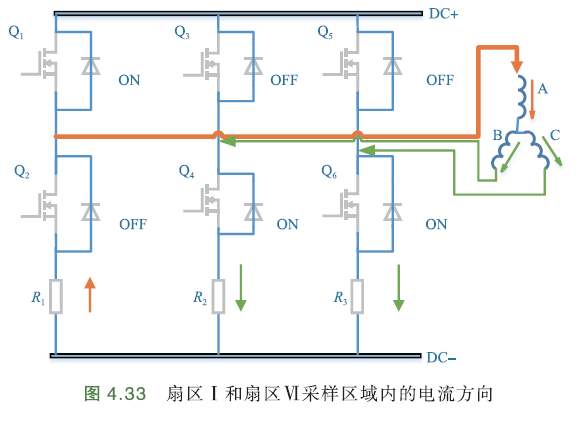
- 扇区Ⅱ、Ⅲ
扇区Ⅱ、Ⅲ七段式调制PWM波形如下图:
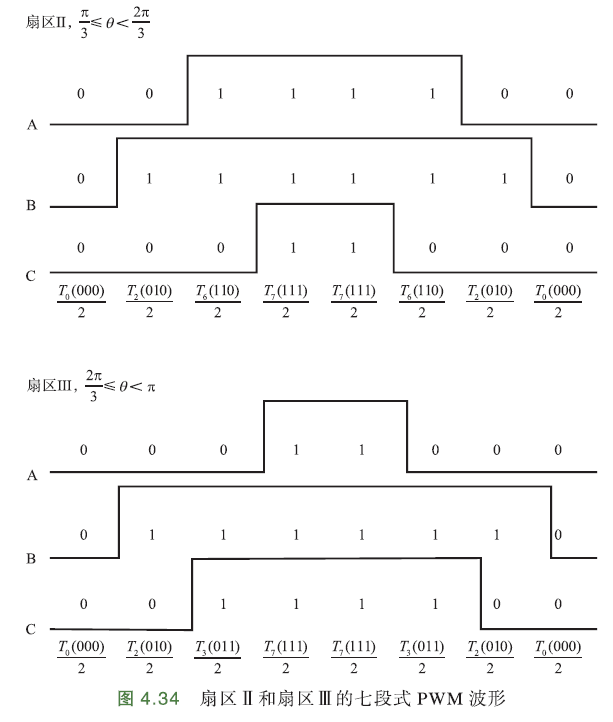
可以看出,2个扇区都是B相上桥臂开通时间最长,下桥臂开通时间最短. 为了采集到有效相电流,可只采集A、C相电流,B相由基尔霍夫电流定律求出.
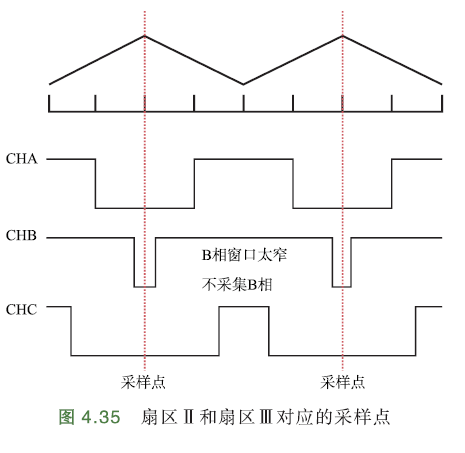
如上图,B相采样窗口太窄,需要避免采集B相.
进入采样区域时,B相上桥臂关断,下桥臂开通,由于电感作用,电流方向不变.
电流流向:电源+ -> B相 -> A相、C相 -> A相、C相的采样电阻 -> 电源-
∴\(I_b\)为正,\(I_a,I_c\)为负
- 扇区Ⅳ、Ⅴ
扇区Ⅳ、Ⅴ七段式调制PWM波形如下图:
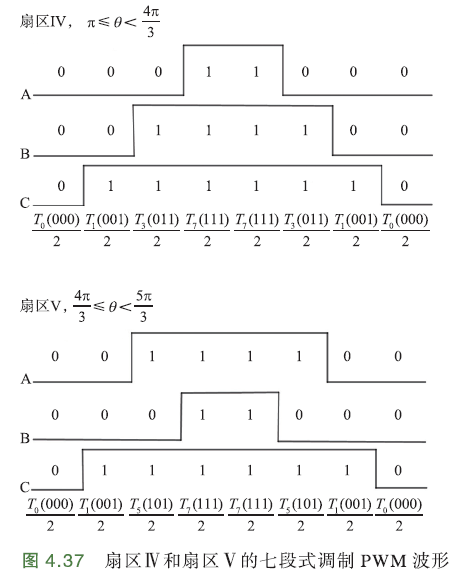
C相上桥臂开通时间最长、下桥臂开通时间最短. 因此,只采集A、B相电流,避免采集C相电流.
采样前一时刻,C相上桥臂为高时,C相直连电源+,B相、A相上桥臂关断,下桥臂连通.
扇区Ⅳ、Ⅴ的七段式调制PWM波形略有不同,但采样点一样、采样区间内电流方向相同. 下图展示了扇区Ⅳ的采样点:
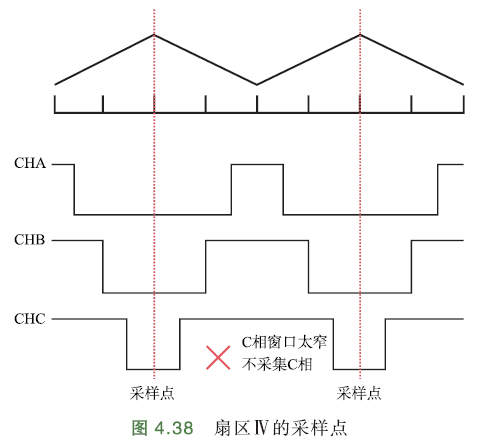
进入采样区域时,C上桥臂关断,下桥臂开通,由于电感作用,电流方向不变
电流流向:电源+ -> C相 -> B相、A相 -> B相、A相上的采样电阻 -> 电源-
∴\(I_c\)为正,\(I_a,I_b\)为负
特点:只需采集一次,就能重构出三相电流,执行速度快. 可避免某一相采样窗口太窄问题,实际应用较多.
标幺化、Q15格式
标幺化电力系统分析和工程计算过程中常用的数值表示方法. 标幺值是各物理量相对于某个基准值而言,表示各物理量及参数的相对值.
例如,实际值380kV电压,如果选取基准值110kV,那么标幺值\(\frac{380}{110}=3.4\)
因为在无刷电机控制系统中,一套电机控制软件可以兼容不同厂家、不同电压、不同功率的电机,用常见MCU处理电压、电流、其他模型参数,运算过程中可能出现实际值变化范围超过MCU字长的问题,难以满足不同电机的变量表示、计算精度要求.
因此,需要标幺化处理. 标幺化弱化不同电机不同数值上的差别,实际计算公式经过标幺化处理,变量的数值形式发生变化,但物理本质未变,所以仍然可以应用各种控制算法,使得计算更简便.
常用Q1.15格式表示<1的浮点数:一共16bit,1bit符号位,其他15bit小数位,即S16格式,范围-32768 ~ +32767.
例如,ST电机库软件用0x49E6表示\(\frac{1}{\sqrt 3}\),即0.57735
浮点数转换为Q15方法:小数x有符号16bit数最大值
32767 x 0.57735=0x49E6
电角度也使用S16格式:-π对应-32768,π对应32767. 在定点MCU中,变量都对标S16格式,极大简化计算. SVPWM计算中,常涉及\(\sqrt 3\),此时可将空间矢量对相电压\(\frac{U_{dc}}{\sqrt 3}\)标幺化:
编码器与测速
编码器
伺服电机的运动控制中,常采用基于矢量技术的电流、速度、位置三闭环控制策略. 相电流可以用采样电阻进行采样.
如何检测速度?
有2类方法:
1)模拟测速;
2)数字测速;
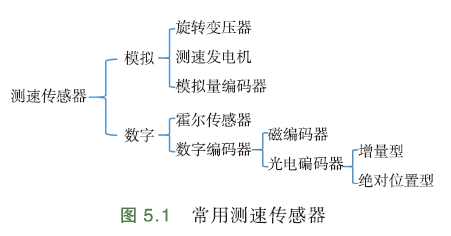
- 模拟测速
通常使用旋转变压器、测速发电机、模拟量编码器,特点:设备体积较大,安装不方便,会增加电机转轴的转动惯量,输出信号噪声较大,现实中较少应用.
- 数字测速
主要有霍尔传感器、数字编码器两种. 霍尔分辨率较低,只能给出转子位置扇区、一些特定位置角,很难适应高精度伺服控制系统;
旋转编码器能提供较高的位置分辨率,目前伺服控制系统中应用较多.
旋转编码器根据实现原理,可分为:磁编码器、光电编码器. 磁编码器受环境影响较大,光电编码器更常用.
常见光电编码器:绝对位置型光电编码器、增量型光电编码器,后者应用较多.
增量型光电编码器,采用光电转换原理,将转速信号转换成脉冲信号. 由光源、码盘、光栅、光电检测元件和转换电路组成. 当电机轴带动码盘旋转时,光线透过码盘和检测光栅上的缝隙照射到光电检测元件上,输出一组相位差90°的类正弦信号,再经过转换电路输出一组规整的正交脉冲信号.
如下图:
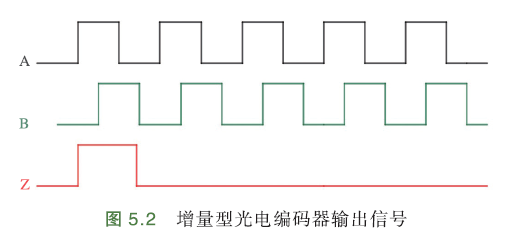
其中, A、B指的是编码器上2个光电检测元件输出的波形,而非无刷电机的三相;Z相零点信号,当编码器旋转到零点时,Z信号发出一个脉冲表示现在是零位置,表示编码器旋转了一圈
特点:低惯量、低噪声、高精度,无法输出旋转轴的绝对位置信号.
增量式光电编码器工作原理,详见:增量式编码器详解
M法测速
周期\(T_c\)内,测量编码器输出的脉冲数\(M_1\)来计算转速. 脉冲数 / 时间 = 编码器输出脉冲的频率,因此M法也称为频率法.
频率:
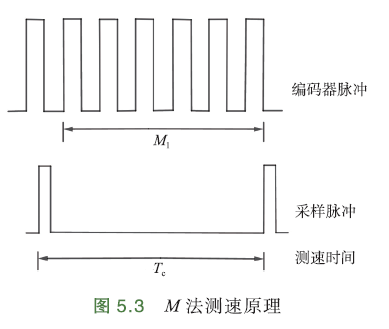
下面探讨M法测速特性.
编码器线数,指编码器转一圈输出多少个脉冲. 例如,如果编码器是500线数,那么一圈会输出500个脉冲,A、B两相转一圈脉冲数一样,不过有90°相位差. 但如果同时检测上升沿、下降沿,那么会产生500x2x2=2000个边沿信号.
设编码器线数M,即一圈产生M个脉冲,那么A、B两相共产生\(N=4M\)个边沿信号.
- 转速
转速:
通常,\(N,T_c\)是常数,所以转速∝脉冲数\(M_1\),因此该测速方法被称为M法.
- 转速的分辨率
当\(M_1\)变成\(M_1+1\)时,转速\(\frac{60M_1}{NT_c}\to \frac{60(M_1+1)}{NT_c}\)
∴M法分辨率:
∴Q是一个常数,与分辨率、转速无关
∴要提高分辨率,降低Q,需要增大编码器线数,或者增大采样周期\(T_c\)
不过,编码器线数、采样周期受现实条件制约,不能无线增大
- 误差率
误差率最大值:
∴转速越高,\(M_1\)越大,误差率越小;相反,转速越低,误差率越大
∴M法不适合低速测量
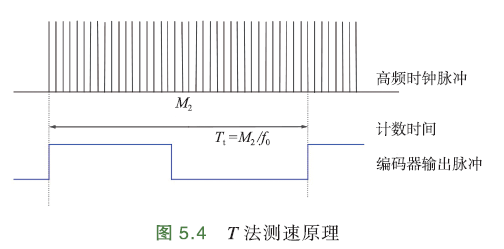
T法测量
通过测量编码器2个脉冲之间的时间间隔来计算转速,称为周期法.
- 转速
假设高频时钟脉冲频率\(f_0\),那么2个脉冲之间时间间隔\(T_t=\frac{M_2}{f_0}\),电机转速:
问题:编码器输出脉冲是Z相?
- 分辨率
当转速变化时,设高频时钟脉冲\(M_2\to M_2-1\),分辨率:
分辨率与转速n相关,转速越小,Q越小,分辨率越高.
- 误差率
最大误差率:
低速下,2个时钟脉冲间隔长,高频时钟脉冲数\(M_2\)多,误差率小,因此适合低速测量.
M/T测速
为兼顾高速、低速,实际常结合M法、T法使用,称为M/T法测速.
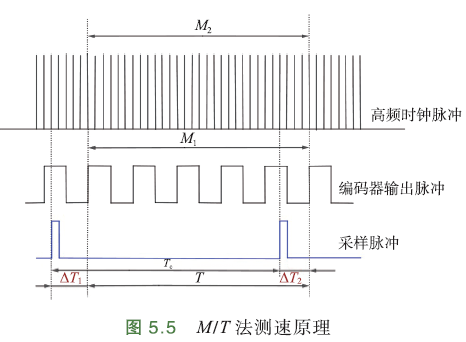
在规定的采样周期\(T_c\)内,同时计数编码器脉冲数\(M_1\)、高频时钟脉冲数\(M_2\),2个计数器严格同步,检测时间与编码器输出脉冲保持一致,以最大限度减少误差.
实际的检测周期T,由\(T_c\)采样脉冲开始后的第一个编码器输出脉冲上升沿决定:
其中,\(ΔT_1\)采样脉冲开始时刻到第一个编码器脉冲上升沿之间的时间间隔,\(ΔT_2\)采样脉冲结束时刻到最后一个编码器脉冲上升沿之间的时间间隔.
检测周期T内电机转过的机械角度:
设编码器每转输出N个脉冲,周期T内编码器输出脉冲数\(M_1\),那么电机转过的机械角度可以表示为:
设高频时钟脉冲频率\(f_0\),检测周期T内时钟脉冲计数值\(M_2\),那么\(T=M_2\cdot \frac{1}{f_0}\)
∴
当转速很高时,\(T_c\gg ΔT_1,ΔT_2\implies T≈T_c\)
当\(M_1\)变化一个脉冲时,可近似认为\(M_2\)不变,分辨率:
∵\(M_2=f_0T_t=f_0T≈f_0T_c\)
∴\(Q≈\frac{60}{NT_c}\) 与M法测速分辨率相同
当转速很低时,\(M_1=1\),转速计算公式与前面T法测速相同
综上,不论低转速,还是高转速,M/T法都有很高的分辨率
电机参数的测量
电机参数的测量是正确调试电机的前提,特别无传感器的调试,参数的正确与否直接影响电机能否正常运行.
电机关键参数:相电阻、相电感、反电动势常数、极对数、转动惯量等.
相电阻
万用表粗略测量,或电桥测量. 万用表两支表笔接电机的任意两相,所得电阻的一半就是相电阻.
三相电机等效测量电路:
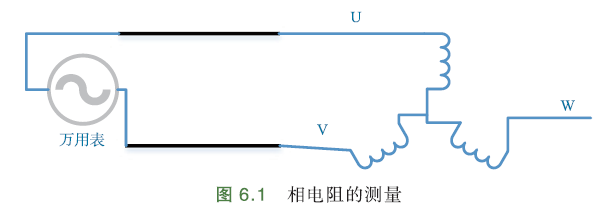
\(R_a,R_b,R_c\)每相等相电阻,\(L_a,L_b,L_c\)每相等效电感
等效电路:
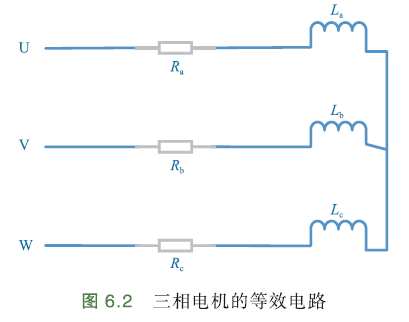
假设万用表的两支表笔分别接三相中任两相,3次测得阻值分别为\(R_1,R_2,R_3\),有
假设电机三相电阻相等,即\(R_a=R_b=R_c\),那么相电阻\(R_s\):
相电感
用电桥测量:频率1kHz,电压1V,测量电机在该频率下电感.
类似于测相电阻,电桥两端接电机任两相,得到的电感值一半、除以3,就是相电感. 可以旋转一周,多次测量求平均值:
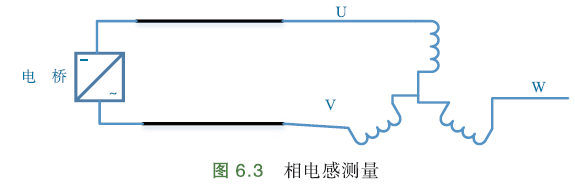
设三相电感相等,即\(L_a=L_b=L_c\),用电桥分别测量电机不同的两相,3次测得结果\(L_1,L_2,L_3\),有
可得相电感\(L_s\):
反电动势常数
电机旋转时,会因切割磁感线产生反电动势,转速越高,反电动势越大,即反电动势∝转速.
一般采用电机对拖方式测量反电动势常数. 小型电机用电动工具带动旋转,运行在发电模式,同时示波器测量任意两相线段电压波形,计算波峰-波谷电压值\(U_{bemf}\)并记录此时转速n. 多次测量后求平均值.
tips:
电机对拖:指将两台同型号或兼容的电机通过机械轴直接或间接连接,其中一台作为驱动电机,另一台作为负载电机,构成一个闭环测试系统,从而完成性能测试、效率分析或参数辨识.
反电动势常数:
其中,\(U_{bemf}\)电机线反电动势的幅值(V);\(ω\)旋转角速度(rad/s);n转速(r/min);\(k_e\)反电动势常数(\(V\cdot s/rad\))
有时,可能遇到单位“V/krpm”,与“V·s/rad”关系:
注意:"rmp"不是规范写法, "r/min"是规范写法.
极对数
由电机厂商给出. 也可自行测量.
示波器测量方法:将示波器的端和地接三相电机的任意两相,用手转动电机一圈,出现的正弦波数量,就是极对数.
这是因为:
转动惯量
电机加减速控制常涉及转动惯量的测量. 转动惯量是表征刚体转动惯性大小的物理量,与刚体质量、质量相当于转轴的分布有关.
电机的转动惯量要与电机轴的负载的惯量尽量匹配,过大、过小都不合适.
常见无刷电机转动惯量的测量方法:自减速法、辅助摆锤法、扭摆法. 下面描述自减速法.
以额定励磁电流驱动电机,当转速 > 额定转速时,让电机空载运转;等电机平稳后,迅速切断电机电源,电机在惯性状态下会继续运行,并自然减速,测量电机的减速曲线.
减速曲线:
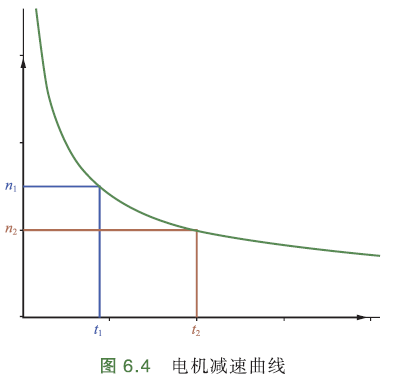
电机转动惯量计算:
其中,J转动惯量(kg·m²);P额定转速下的机械损耗和空载铁损之和(kW);\(n_1\)为\(t_1\)时刻的转速(r/min);\(n_2\)为\(t_2\)时刻的转速(r/min)
参考
[1]上官致远,张健.深入理解无刷直流电机矢量控制技术[M].科学出版社,2020.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号