FOC算法笔记

目录

无刷电机结构

基本航模无刷电机结构图：

img

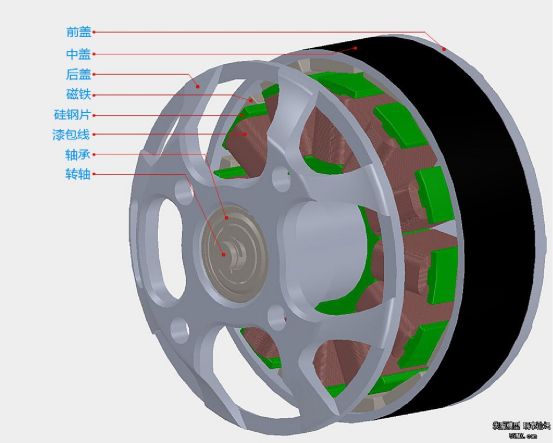
由前盖、中盖、后盖、磁铁、硅钢片、漆包线、轴承、转轴组成.

宏观上，分为2部分：

  • 定子：有线圈绕组，固定不动的部分；
  • 转子：电机旋转的部分，用于输出电机的转动和扭矩

无刷电机，分为内转子、外转子2种：

  • 内转子无刷电机：转子在内部；
  • 外转子无刷电机：转子在外面，最常见.

内转子：
img

外转子：
img

直流无刷电机驱动：依靠改变电机定子线圈电流交变频率和波形，在定子周围形成磁场，驱动转子永磁体转动，进而带动电机转动起来.
要让电机转动，研究如何改变定子线圈的电流交变频率、波形，是工作重点.

可分为2部分进行研究：硬件电路、软件控制.

无刷电机硬件控制原理

无刷电机与有刷电机区别

有刷电机可通过碳刷换相，实现电流换向.
无刷电机没有碳刷，需要通过MOS管实现电子换向.

MOS管本质是一种开关，可通过MCU IO口控制通断.

场景3种封装MOS管：

img

无刷电机控制的硬件原理

通过控制MOS管通断的组合，电机线圈中电流大小、方向就能改变.

如下图Q1、Q2导通，电流从DC+➡Q1➡A相流入➡B相流出➡DC-.

img

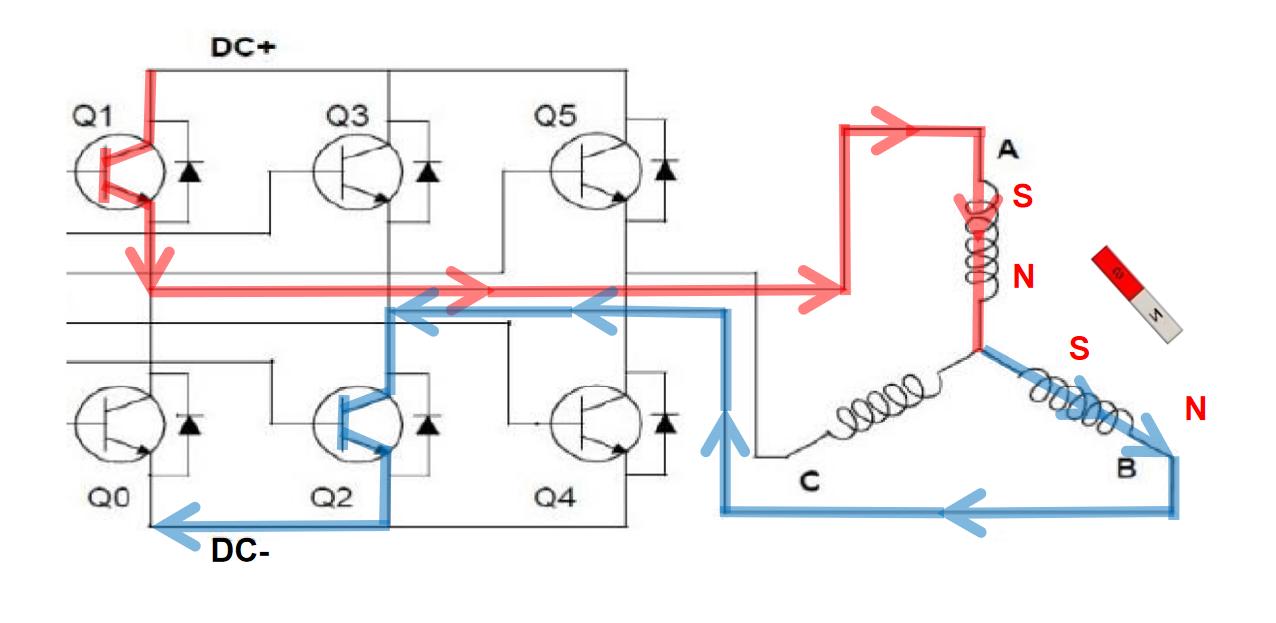
根据右手螺旋定则，定子A线圈通电，产生感应磁场，方向由S➡N；同时，B线圈，也会产生该用磁场，方向S➡N.

此时，可简单将转子抽象成一块磁铁.

如何让电机动起来？

img

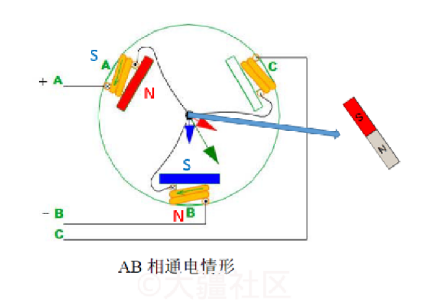
由于感应磁场的影响，定子线圈会吸引转子的磁铁转动. 但是，转子磁铁旋转一定角度后，磁铁会停止不动，必须改变电磁场状态（感应磁场方向），才能让转子继续转动.

如何让电机继续转动？

img

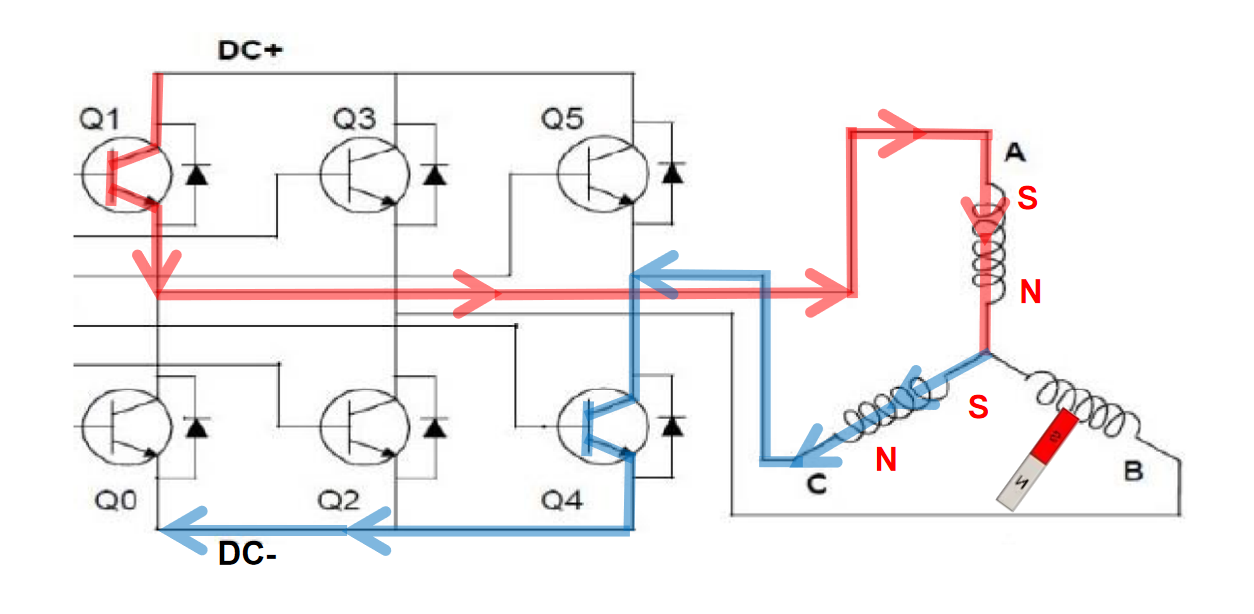
接下来，打开Q1、Q4管. 根据右手螺旋定则，磁场方向改变，转子磁场进而旋转.

因此，只需要交替开关不同的MOS管，就能实现电机磁极的交替运动.
—— 这就是 无刷电机旋转运动的原理.

img

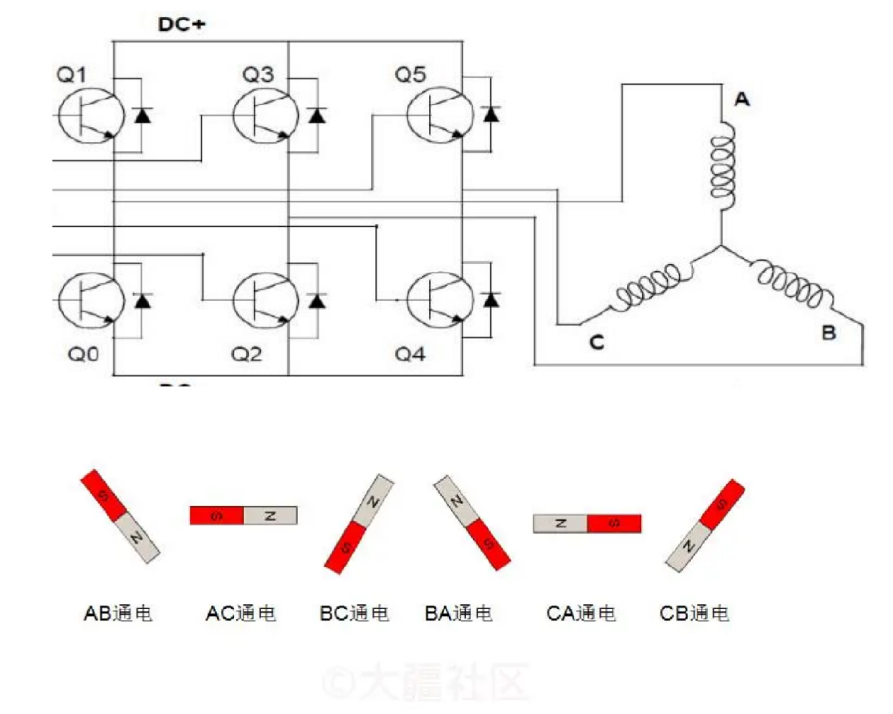
如上图，是转子磁铁旋转一周时，各个相的通电情况. 只需要交替开关各个相的MOS管即可，从而实现电机的转动. 当MOS管开关速度变快，就可以加速转子的转动；开关速度变慢，转子转动变慢.

∴电机控制 == 对MOS管开关规律的控制

∴ MOS管的开关，需要用到MCU程序控制

这就引出了FOC控制算法.

FOC算法

FOC控制算法（磁场定向控制算法）：对电机运动模型进行抽象化和简化，进而有规律的控制各个MOS管开关和通断的过程.

克拉克变换、帕克变换，是FOC算法2个核心.

FOC控制原理

FOC的过程，就是将需求的电机力矩，转化成最终的3相电力输出，并且让电机物理输出所需的力矩的过程.

这也被称为电机控制三环中的力矩环. 后面的位置闭环、速度闭环，都得基于这个力矩环.

这个力矩环的算法，就是一个无刷电机旋转状态的数学模型.

img

克拉克变换

之前，已经知道交替开关MOS，可实现电机转动. 交替开关的MOS，是以极快的周期进行的.

将这些周期性开启、关断的过程联系起来，对其各个相进行单独观察，可得到3个相——A、B、C相的电流随时间变化的曲线.

3个相的曲线，存在120°相位差；3个相电流，分别对应3个定子线圈上的电流.

img

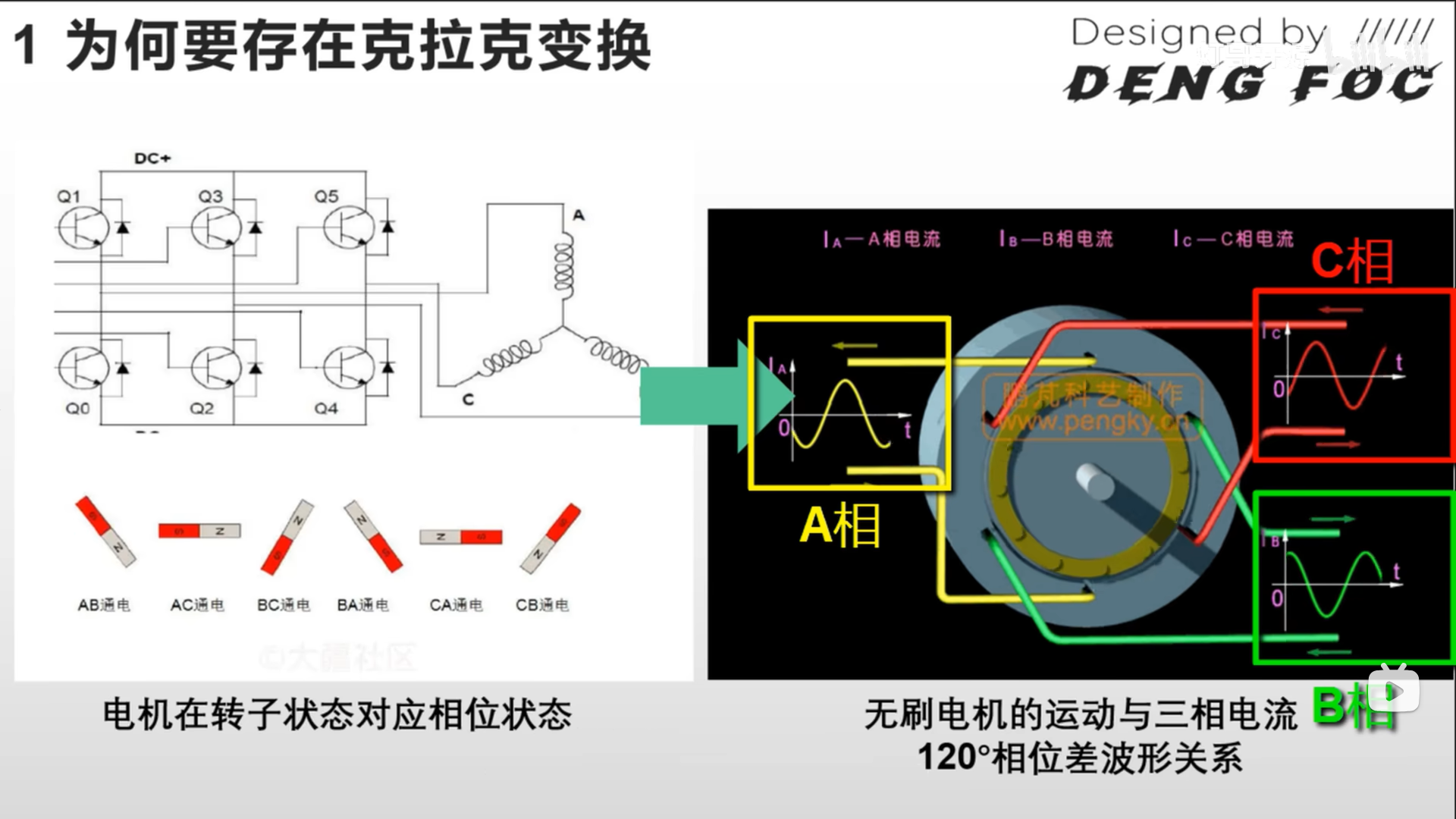
如何调制出相位差120°的sin波形？

极难控制、改变参数. 因为

1）相与相之间，相互耦合，MOS管一旦打开，则至少打开2个相.

2）如果只想改变一个相的波形，来实现电机控制，不可行. 需要多个相位协作，一起改变，才能实现电机控制

这个问题涉及3相相位差120°的波形，很复杂，能否降维度？

可用克拉克变换.

克拉克变换(Clarke Transform)，实际是降维、解耦的过程，将难以辨明、控制的三相相位差120°电机波形降维为二维矢量.

步骤：

1）矢量化：三相随时间变换的，相位差为120°的电流波形抽象化为三个间隔120°的矢量

三相电流\(I_A,I_B,I_C\)，对应平面上基的夹角为120°的坐标系\([O;\bm{I_a},\bm{I_b},\bm{I_c}]\)上3个基向量上的矢量（有大小、方向）

img

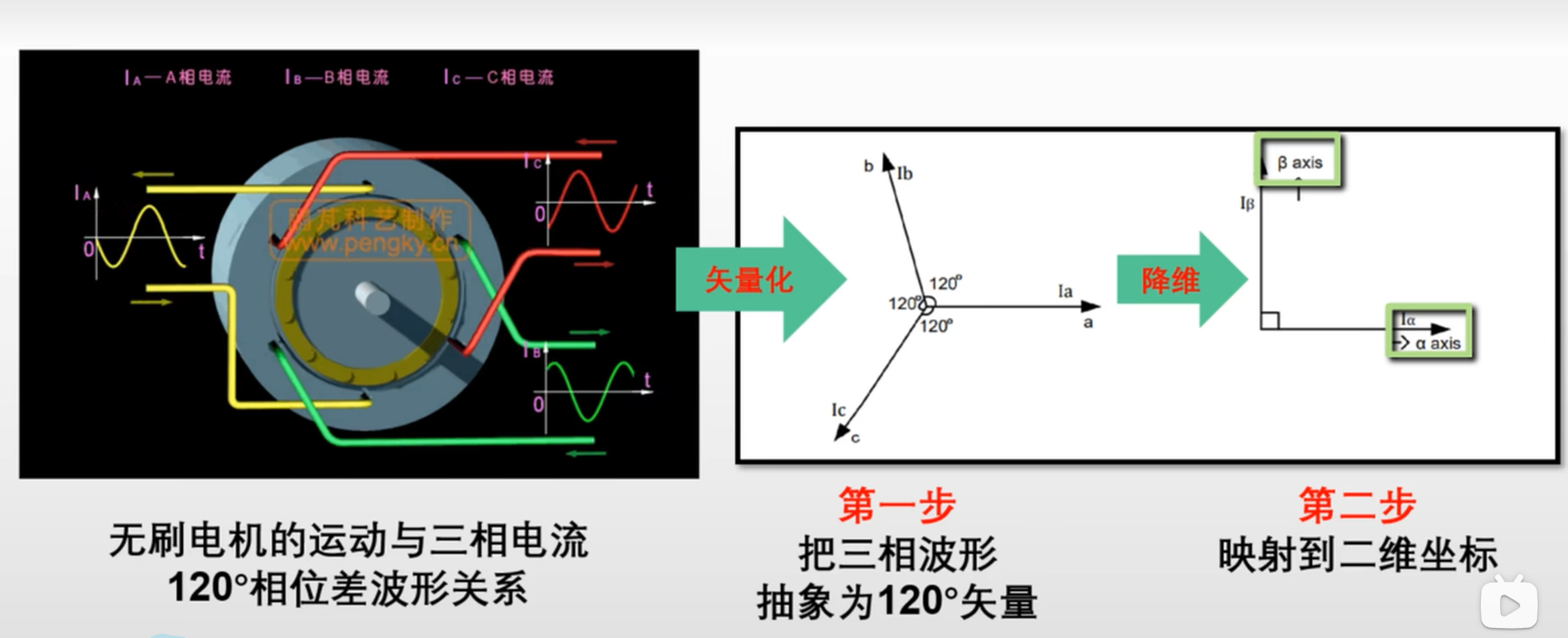
2）投影：利用三角函数对矢量进行降维，降维到两个坐标轴

三维坐标系\(ABC\)（非直角坐标系）降为二维坐标系\(αβ\)（直角坐标系），这个过程称为投影（不同于图形学中的透视投影）

下面推导投影过程：

img

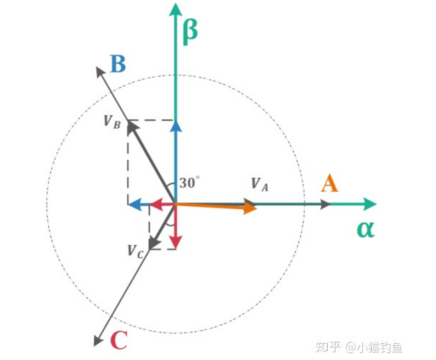
α与A方向相同，将A、B、C方向上的矢量\(i_a,i_b,i_c\)均投影到α、β方向上，有

\[\begin{aligned} I_α &= i_a-sin 30°i_b-cos 60°i_c=i_a-\frac{1}{2}i_b-\frac{1}{2}i_c\\ I_β &= cos 30°i_b-sin 60°i_c=\frac{\sqrt{3}}{2}i_b-\frac{\sqrt{3}}{2}i_c \end{aligned} \]

写成矩阵形式，即克拉克变换的基本形式

\[\begin{bmatrix} I_α\\I_β \end{bmatrix} =\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} \]

等幅值变换形式

很多文献上，克拉克变换对应形式不一样，而是加上一个系数，如\(\frac{2}{3}\)（等幅值变换系数）、\(\sqrt{\frac{2}{3}}\)（等功率变换系数），分别对应不同变换方式：等幅值变换形式、等功率变换形式.

等幅值变换形式：

\[\begin{bmatrix} I_α\\I_β \end{bmatrix} =\frac{2}{3}\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} \]

什么是等幅值变换？

克拉克变换前后，电流、电压的幅值不变. 下面以电压证明为例.

∵3相电压、电流是相位差120°的正弦（或余弦）波形
∴可设三相电压、电流表示：

\[\begin{cases} i_a = I_mcos(θ)\\ i_b = I_mcos(θ+\frac{2π}{3})\\ i_c = I_mcos(θ-\frac{2π}{3}) \end{cases}, \begin{cases} u_a = V_mcos(θ)\\ u_b = V_mcos(θ+\frac{2π}{3})\\ u_c = V_mcos(θ-\frac{2π}{3}) \end{cases} \]

其中，\(V_m、I_m\)是相电压、相电流的幅值，\(θ=ωt\)是电角度

相关概念，可参见电路基础：交流电路

设变换T，将ABC坐标系下坐标\((u_a,u_b,u_c)\)变换到αβ坐标系下\((u_α,u_β)\)坐标
于是，

\[\begin{bmatrix} i_α\\i_β \end{bmatrix} =T\cdot \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} \]

∵变换前后幅值不变
∴\(\sqrt{i_α^2+i_β^2}=I_m\)

∵T是克拉克变换的特殊形式
∴

\[T=k\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \]

由基尔霍夫定律，\(i_a+i+i_c=0\)

∴

\[\begin{cases} i_α=\frac{3}{2}ki_a\\ i_β=\frac{\sqrt 3}{2}k(i_b-i_c) \end{cases} \]

∴\(i_b-i_c=I_m[cos(θ+\frac{2π}{3})-cos(θ-\frac{2π}{3})]=-\sqrt 3 I_m sinθ\)

∴

\[\begin{aligned} i_α^2+i_β^2 &= \frac{9}{4}k^2i_a^2+\frac{3}{4}k^2(i_b-i_c)^2\\ &= \frac{3}{4}k^2[3i_a^2+(i_b-i_c)^2]\\ &= \frac{3}{4}k^2I_m[3cos^2 θ + 3sin^2 θ]\\ &= \frac{9}{4}k^2I_m^2 = I_m^2\\ \implies k^2 &= \frac{4}{9}\\ k &= ±\frac{2}{3} \end{aligned} \]

∵\(i_a\)和\(i_α\)方向相同
∴取\(k=\frac{2}{3}\)

用等幅值变换有什么好处？

可以确保变换前后，\(i_a\to i_α\)不变.

\[\begin{cases} i_α=i_a\\ i_β=\frac{1}{\sqrt 3}i_b-\frac{1}{\sqrt 3}i_c \end{cases} \]

等功率变换形式

等功率变换形式：

\[\begin{bmatrix} I_α\\I_β \end{bmatrix} =\sqrt{\frac{2}{3}}\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} \]

等功率变换特点：变换前后，功率不变，即\(P_{abc}=P_{αβ}\)
其中，

\[\begin{aligned} P_{abc} &= u_ai_a+u_bi_b+u_ci_c\\ P_{αβ} &= u_αi_α+u_βi_β \end{aligned} \]

设变换T，使得

\[\begin{bmatrix} u_α\\u_β \end{bmatrix} =T\cdot \begin{bmatrix} u_a\\u_b\\u_c \end{bmatrix}, \begin{bmatrix} i_α\\i_β \end{bmatrix} =T\cdot \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} \]

其中，

\[T=k\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \]

∴

\[\begin{cases} u_α=\frac{3}{2}ku_a\\ u_β=\frac{\sqrt 3}{2}k(u_b-u_c) \end{cases}, \begin{cases} i_α=\frac{3}{2}ki_a\\ i_β=\frac{\sqrt 3}{2}k(i_b-i_c) \end{cases} \]

∴\(i_b-i_c=-\sqrt 3 I_m sinθ, u_b-u_c=-\sqrt 3 V_m sinθ\)

有

\[\begin{aligned} P_{abc} &= u_ai_a+u_bi_b+u_ci_c\\ &= V_mI_m[cos^2 θ + cos^2 (θ+\frac{2π}{3})+cos^2 (θ-\frac{2π}{3})]\\ &= \frac{3}{2}V_mI_m \end{aligned} \]

\[\begin{aligned} P_{αβ} &= u_αi_α+u_βi_β\\ &= \frac{9}{4}k^2u_αi_α+\frac{3}{4}k^2(u_b-u_c)(i_b-i_c)\\ &= \frac{3}{4}k^2[3u_αi_α + (u_b-u_c)(i_b-i_c)]\\ &= \frac{3}{4}k^2[3V_mI_mcos^2 θ + (-\sqrt 3 I_m sinθ)(-\sqrt 3 V_m sinθ)]\\ &= \frac{3}{4}k^2 \cdot [3V_mI_m(cos^2 θ + sin^2 θ)]\\ &= \frac{9}{4}k^2V_mI_m=P_{abc}=\frac{3}{2}V_mI_m\\ \implies k &= ±\sqrt \frac{2}{3} \end{aligned} \]

∵\(i_α,i_a\)同方向
∴取\(k=\sqrt \frac{2}{3}\)

克拉克逆变换

克拉克变换，是将三相时域上的复杂问题（电流随时间变化的正弦波，相位差120°）转化为二维矢量表示，降维、简化问题.
即：

\[(i_a,i_b,i_c)\to (i_α,i_β) \]

克拉克逆变换，是克拉克变换的逆过程，由二维矢量形式重新升维变回原来的三相电流波形：

\[(i_α,i_β)\to (i_a,i_b,i_c) \]

为简化计算，后面我们不用克拉克变换基本形式，而是用等幅值变换形式，即

\[\begin{cases} i_α = i_a\\ i_β = \frac{1}{\sqrt 3}(i_b-i_c)=\frac{1}{\sqrt 3}(2i_b+i_a) \end{cases} \]

求逆变换：

\[\begin{aligned} i_a &= i_α\\ i_b &= \frac{\sqrt 3 i_β - i_α}{2}\\ i_c &= -(i_a+i_b)=-\frac{\sqrt 3 i_β + i_α}{2} \end{aligned} \]

于是，

克拉克逆变换：

\[\begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} = \begin{bmatrix} 1 & 0\\ -\frac{1}{2} & \frac{\sqrt 3}{2}\\ -\frac{1}{2} & -\frac{\sqrt 3}{2} \end{bmatrix} \begin{bmatrix} i_α\\i_β \end{bmatrix} \]

帕克变换

克拉克变换将电机的正弦驱动的三相曲线，从ABC坐标系转换到αβ坐标系，进行了降维，但是没有将其与电机的旋转对应起来. 我们需要建立电机旋转时的数学模型，也就是旋转时的\(i_α,i_β\)电流规律，来解决该问题.

帕克变换（Park Transform），就是这样一个数学模型，能帮我们求得各种旋转情况下的\(i_α,i_β\).

思路：

1）将电机的定子线圈上建立\(αβ\)坐标系（局部坐标系），在坐标系右边放一个转子（SN极对）

如果转子不动，那么\(αβ\)坐标系中，肯定有一对\(i_α,i_β\)对应此时转子状态；然而，实际应用中，转子是时刻转动的，于是，想到在转子上也建立局部坐标系.

img

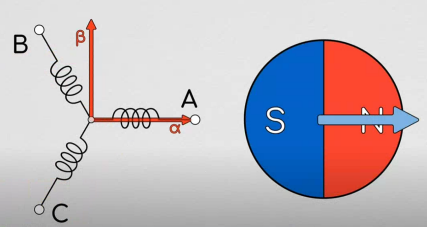
2）在转子上建立\(dq\)坐标系（局部坐标系）

下图是将2个坐标系画到一起，原点重合：

img

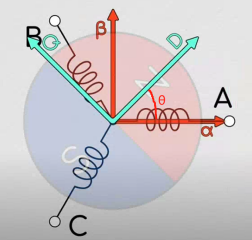
其中，\(dq\)坐标系随转子转动，D轴指向电机N级，\(αβ\)坐标系跟定子固定不动. \(dq\)坐标轴因转动而造成的与\(αβ\)坐标轴的差角\(θ\)，称为电角度.

于是，我们可以2个坐标系的关系，求出\(i_d,i_q\)与\(i_α,i_β\)的变换关系：

img

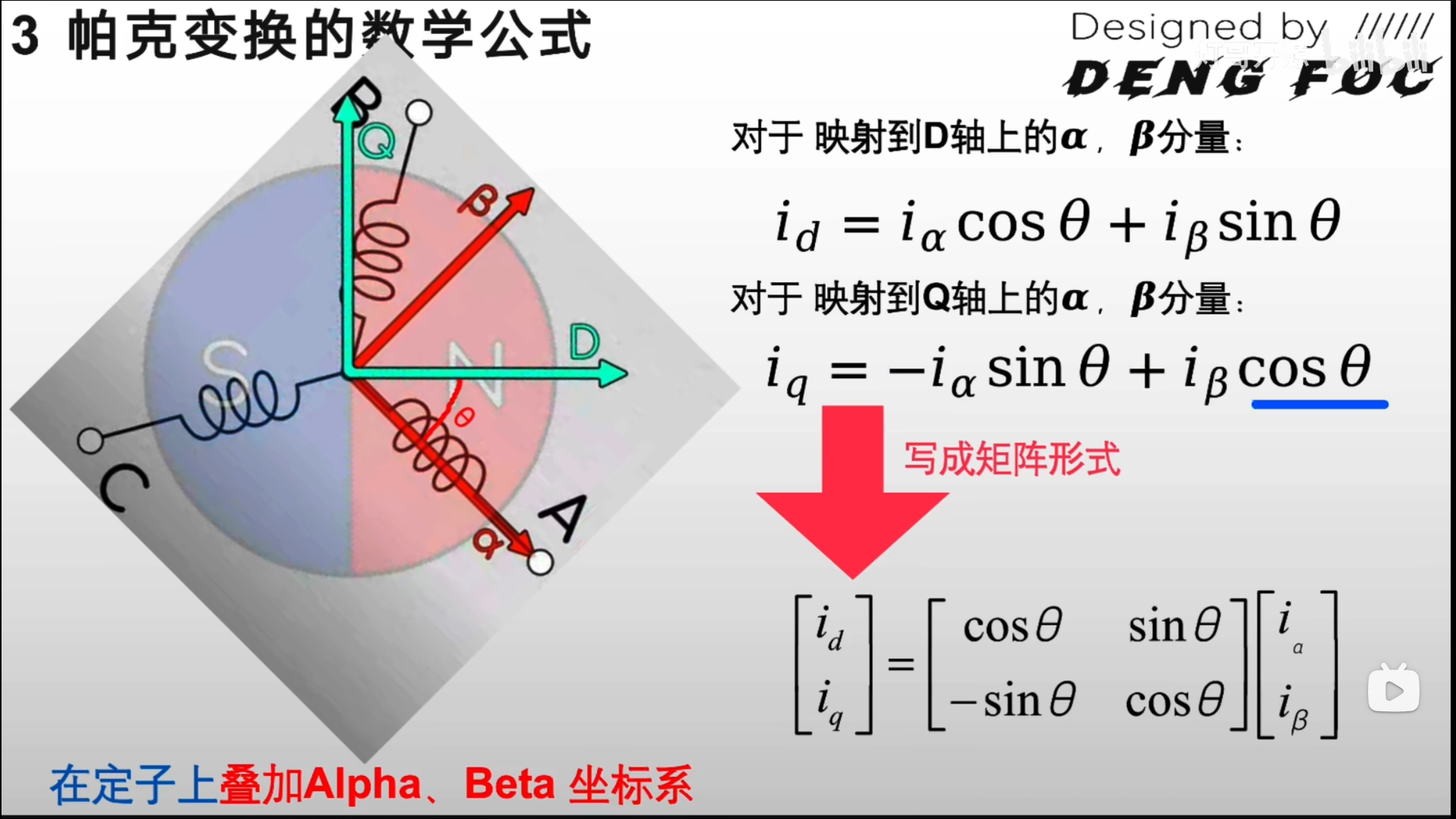
电流映射到D轴上α、β分量：

\[i_d = i_α cos θ + i_β sin θ \]

电流映射到Q轴上α、β分量：

\[i_q = -i_α sin θ + i_β cos θ \]

对应变换矩阵：

帕克变换：

\[\begin{bmatrix} i_d\\i_q \end{bmatrix} =\begin{bmatrix} cos θ & sin θ\\ -sin θ & cos θ \end{bmatrix} \begin{bmatrix} i_α\\i_β \end{bmatrix} \]

这个形式，是不是跟计算机图形：三维几何变换 绕主轴旋转很像？为什么sin项的符号相反呢？

答：

帕克变换中的旋转，是将坐标轴旋转，求出同一个点在旋转后坐标系下的坐标，即坐标轴的旋转；
而图形学中的旋转，通常指将点绕坐标轴旋转，求出旋转后的点在原坐标系下的坐标，即点的旋转；

也就是说，它们衡量坐标的坐标系不同，2个变换互为逆变换.

图形学中，点\((x,y)\)绕z轴旋转θ角，得到\((x',y')\)坐标，对应旋转变换\(R(θ,z)\)：

\[R(θ,z)=\begin{bmatrix} cos θ & -sin θ\\ sin θ & cos θ \end{bmatrix} \]

克拉克变换，对应旋转变换\(R(-θ,z)\)：

\[R(-θ,z)=\begin{bmatrix} cos θ & sin θ\\ -sin θ & cos θ \end{bmatrix} \]

注意：
1）二维旋转，可看成三维\(xyz\)坐标系下，绕z轴旋转，θ正方向通常规定为逆时针方向.
2）坐标系变换 = 原点的平移变换 + 坐标轴（或基）的旋转变换，由于原点重合，所以忽略平移变换

根据旋转的逆变换特性，很容易得到帕克变换的逆变换\(R(θ,z)=R(-θ,z)^{-1}\)：

帕克逆变换：

\[\begin{bmatrix} i_d\\i_q \end{bmatrix} =\begin{bmatrix} cos θ & -sin θ\\ sin θ & cos θ \end{bmatrix} \begin{bmatrix} i_α\\i_β \end{bmatrix} \]

实际应用中，如何应用帕克变换（逆变换）？

答：实际FOC应用中，电角度可由编码器（如AS5047P,AS5600）求出，\(i_q, i_d\)可合成一个矢量，通过帕克逆变换求出\(i_α, i_β\)，进而通过克拉克逆变换求出\(i_a,i_b,i_c\).

简单FOC应用中，只需要控制\(i_q\)电流，而将\(i_d=0\). 而\(i_q\)决定电机力矩. 当我们所需力矩确定时，就能确定\(i_q\)，进而决定\(i_a,i_b,i_c\)三相电流大小.

什么是简单FOC应用，可设\(i_d=0\)？

答：
适合场景：
1）PMSM（永磁同步电机）在基速以下，且无需弱磁时，如伺服电机、无人机电调；
2）对控制复杂度敏感的FOC应用，需要简化FOC实现.

不适合场景：
1）高速运行，需要弱磁；
2）感应电机，或IPMSM，需利用磁阻转矩或励磁.

这里不细说，后面如有需要会继续研究.

小结

img

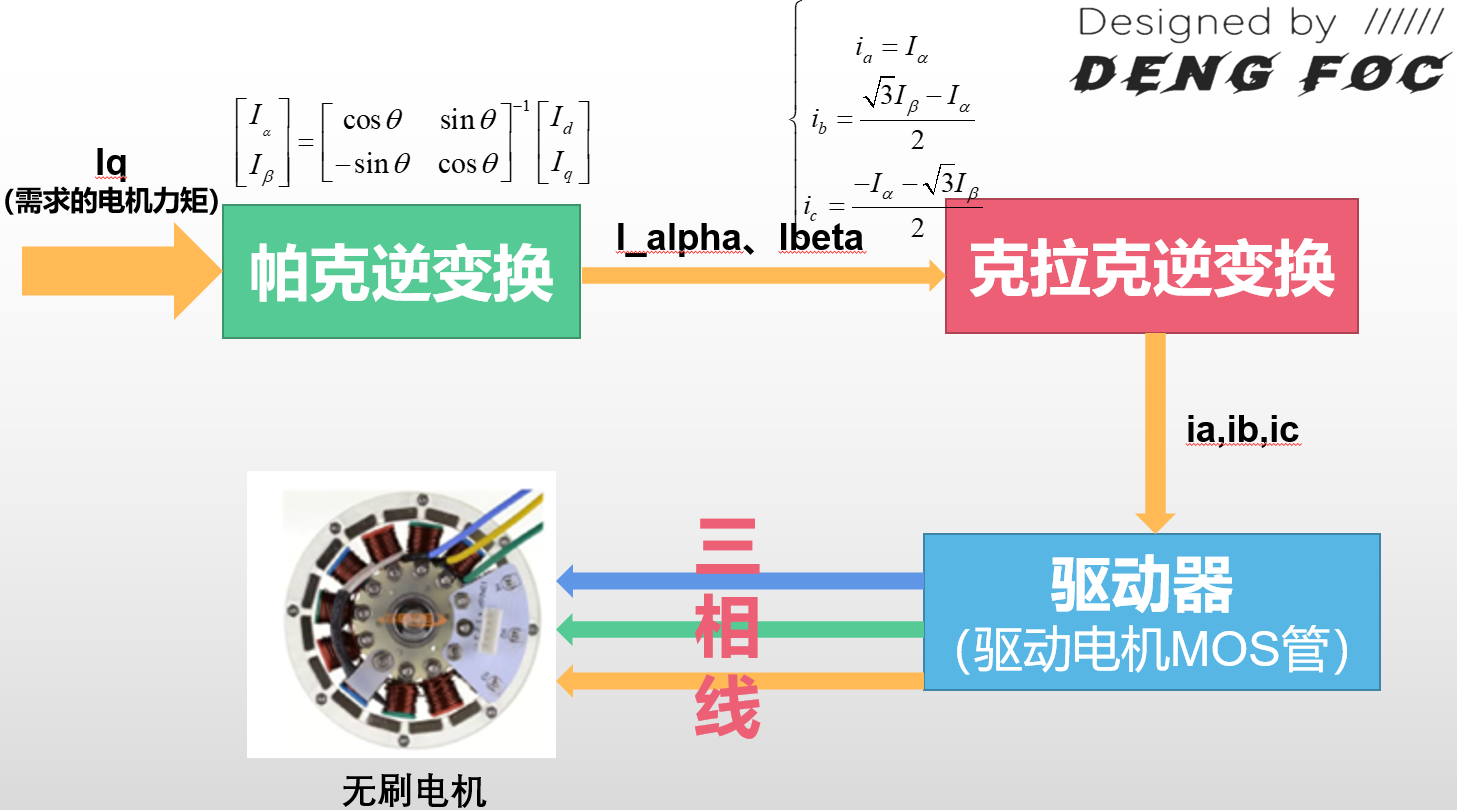
FOC控制电机过程：输入需求力矩，最后得到真实世界输出力矩的过程. 其中，用帕克逆变换将\(i_q,i_d\)转换为\(i_α,i_β\)，克拉克逆变换将\(i_α,i_β\)转化为三相电流\(i_a,i_b,i_c\).

MCU在其中，扮演通过程序将\(i_a,i_b,i_c\)转化为对MOS管的开关信号.

FOC开环速度

开环速度原理

三相电压矢量

img

前面推导，都是针对电流的，而MCU能直接控制的，是MOS管通断，即对电压信号\(u_a,u_b,u_c\)的控制. 而\(i_a,i_b,i_c\)的控制，必须在控制\(u_a,u_b,u_c\)的基础上，通过各相电流传感器作闭环，才能进一步实现电流的控制.

因此，需要知道FOC过程中，电压的转换关系.

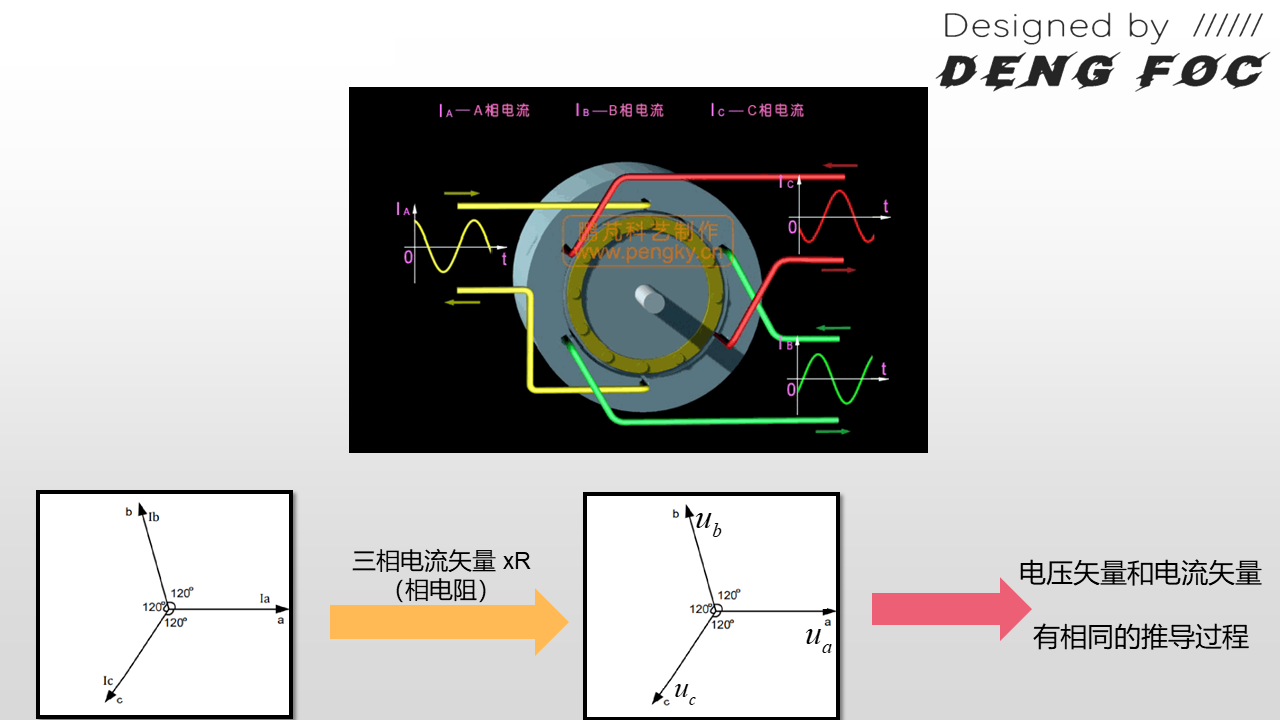
三相电路中，每一相线圈都有相同的相电阻R，根据欧姆定律，相电流\(i_a,i_b,i_c\)×R，可得到相电压\(u_a,u_b,u_c\)

∴电压矢量和电流矢量推导过程相同

img

上图展示了电流、电压形式的 帕克逆变换、克拉克逆变换.

开环速度代码编写

总流程：

img

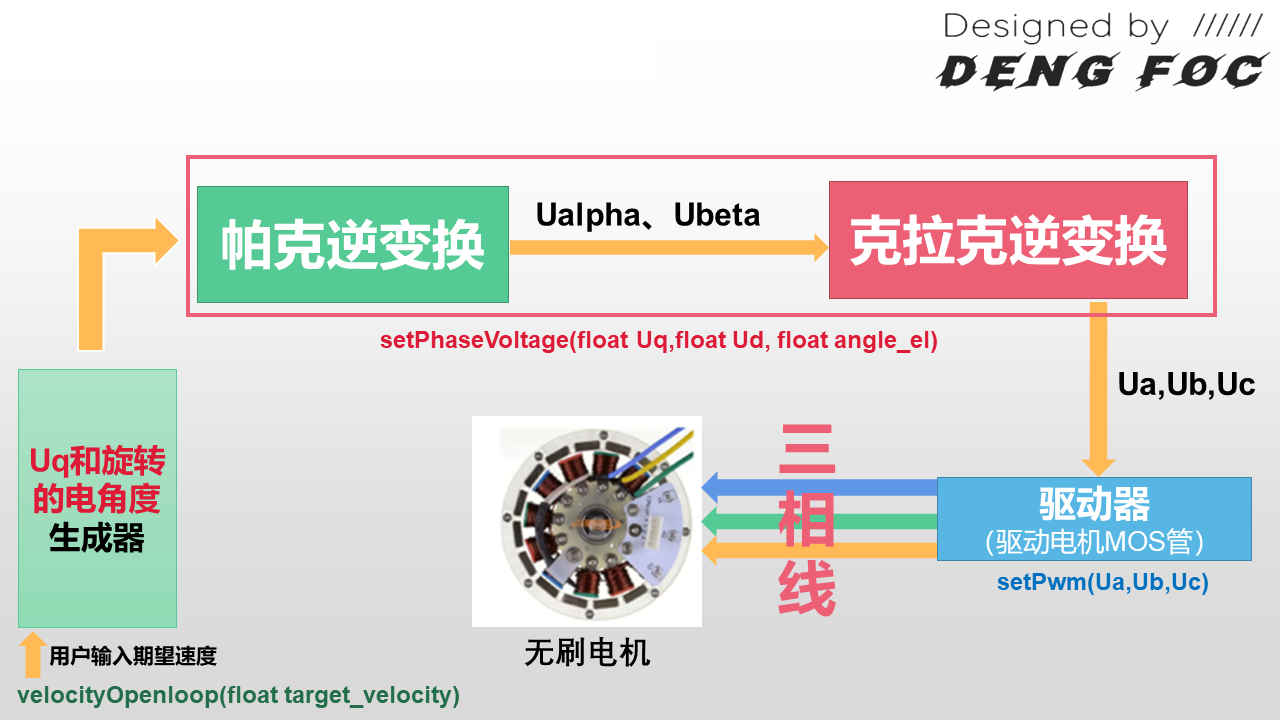
开环速度控制过程：由用户输入期望速度，然后通过Uq和旋转电角度生成器得到Uq,Ud(Ud=0)，θ，再通过帕克逆变换得到Uα,Uβ，接着通过克拉克逆变换得到Ua,Ub,Uc，最后通过驱动器（MOS管）对三相电压进行PWM控制，从而实现对电机速度的控制.

关键函数：

  • setPhaseVoltage：给定\(U_q, θ\)，实现帕克逆变换、克拉克逆变换，计算出电机控制需要的\(u_a,u_b,u_c\)，并通过setPWM传递给电机驱动器硬件，硬件就会产生三相电压波形控制电机

  • velocityOpenloop：根据用户输入的目标电机转速target_velocity，算出该速度下的\(U_q\)、电角度\(θ\)，然后传递给setPhaseVoltage

  • setPwm: 给定\(U_a,U_b,U_c\)，计算出PWM占空比，并设置PWM硬件电路产生对应PWM波

setPhaseVoltage

setPhaseVoltage实现：

img

注意：简单FOC应用中，\(i_d=0,u_d=0\)

float voltage_power_supply = 12.6;

// angle_el 电角度
void setPhaseVoltage(float Uq, float Ud, float angle_el) {
    angle_el = _normalizeAngle(angle_el + zero_electric_angle);
    // 帕克逆变换
    Ualpha = -Uq * sin(angle_el);
    Ubeta  =  Uq * cos(angle_el);

    // 克拉克逆变换
    Ua = Ualpha + voltage_power_supply / 2;
    Ub = (sqrt(3) * Ubeta - Ualpha) / 2 + voltage_power_supply / 2;
    Uc = (-Ualpha - sqrt(3) * Ubeta) / 2 + voltage_power_supply / 2;
    setPwm(Ua, Ub, Uc);
}

// 角度归一化到 [0, 2π]
float _normalizeAngle(float angle) {
    float a = fmod(angle, 2 * M_PI); // 取余运算: a = angle % 2π
    return a >= 0 ? a : (a + 2 * M_PI);
}

代码中，我们给每个\(u_a,u_b,u_c\)都加了voltage_power_supply/2偏移（voltage_power_supply是板子的电源电压），这是因为原始\(u_a,u_b,u_c\)是正弦曲线输出形式，会有电压 < 0部分，而实际电路中，很难产生负电压. 为了避免产生电压 < 0的部分，我们将\(u_a,u_b,u_c\)加上voltage_power_supply/2偏移.

如果不加电压偏移voltage_power_supply/2，实际ua,ub,uc曲线的0点从0V开始，后续会产生负向电压，而负电压是不可接受的：

img

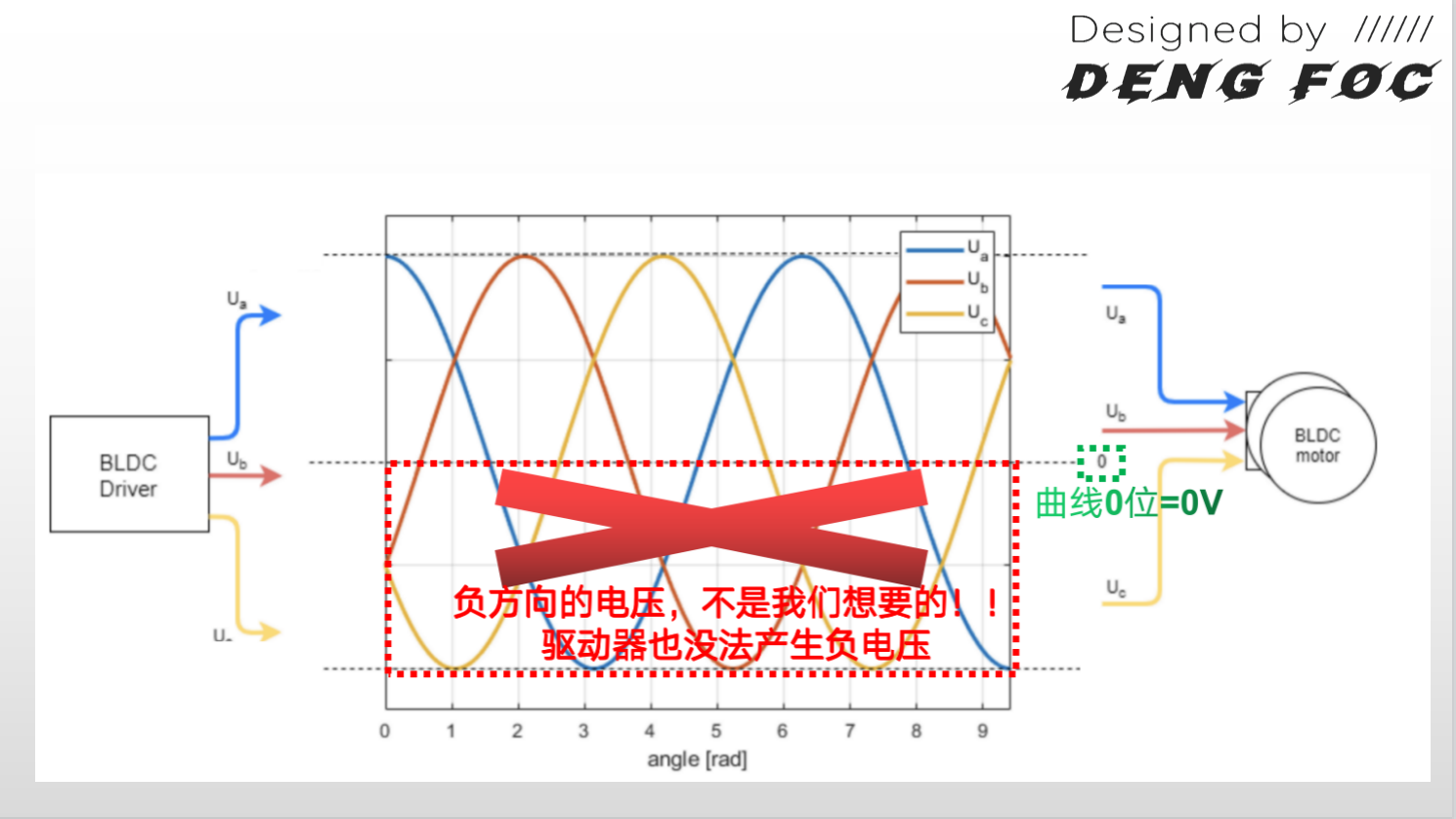
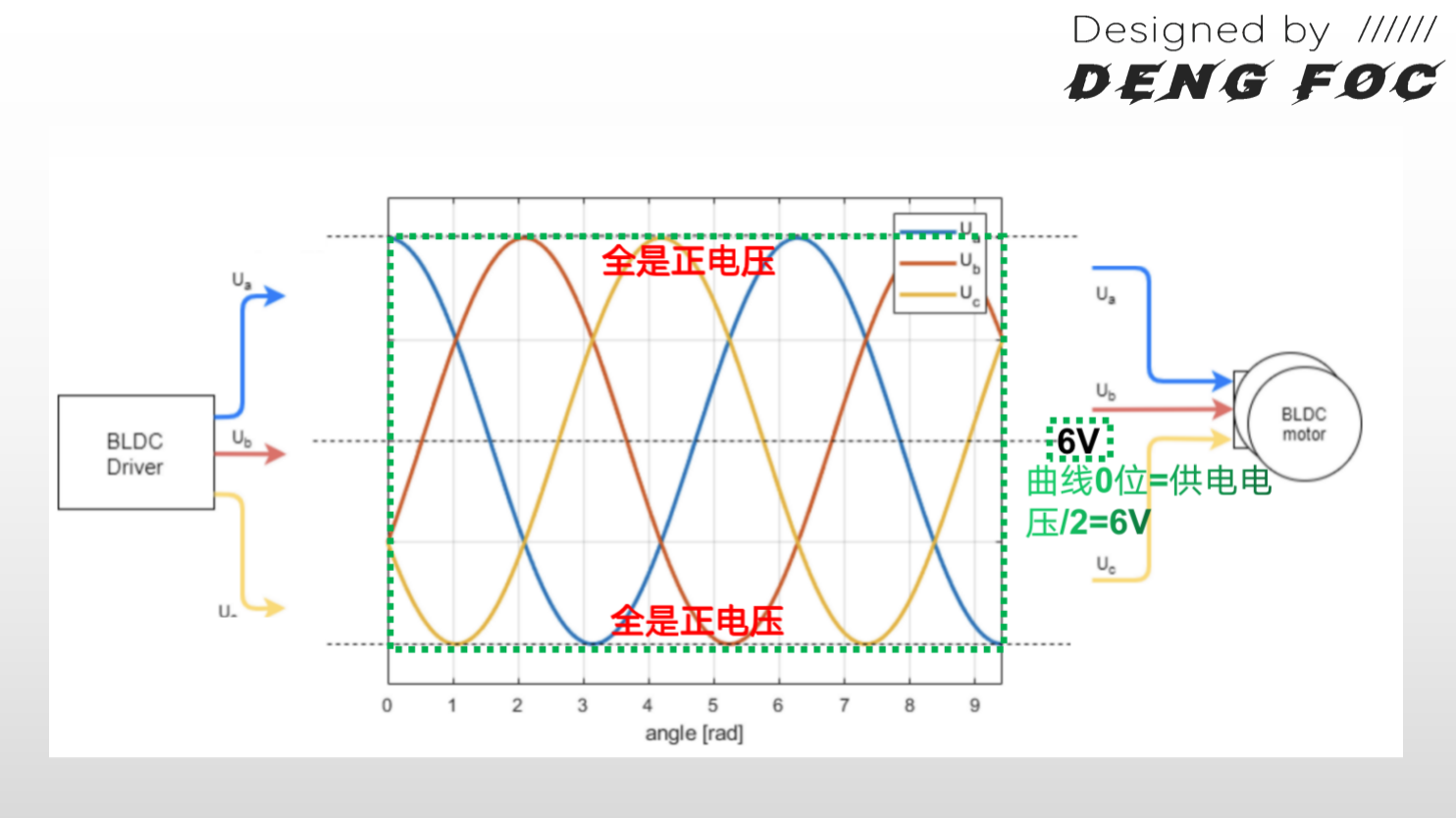
如果加上电压偏移voltage_power_supply/2，实际ua,ub,uc曲线0点从6V开始，ua,ub,uc的变化范围就是±6V：

img

setPwm

setPwm实现：
img

通过PWM占空比，控制一个PWM波形周期内的平均电压，从而实现期望的\(U_a,U_b,U_c\).

如何计算一个PWM波形周期内的平均电压与占空比关系？

设MCU电压（PWM高电平）\(Vcc=5V\)，低电平0V，周期T，占空比为d（\(d\in[0,1]\)），那么输出平均电压：

\[V_{avg}=Vcc\cdot d\cdot T/T=Vcc\cdot d \]

例如，
1）占空比为 50%， 那么平均电压 $ V_{avg}=5V\cdot 0.5=2.5V $

2）占空比为 75%， 那么平均电压 $ V_{avg}=5V\cdot 0.75=3.75V $

3）占空比为 20%，那么平均电压 $ V_{avg}=5V\cdot 0.20=1V $

// 约束函数, 限制值范围
#define _constrain(amt, low, high) ((amt) < (low) ? (low) : ((amt) > (high) ? (high) : (amt)))

// 设置PWM到控制器输出
void setPwm(float Ua, float Ub, float Uc) {
    // 限制上限
    Ua = _constrain(Ua, 0.0f, voltage_limit);
    Ub = _constrain(Ub, 0.0f, voltage_limit);
    Uc = _constrain(Uc, 0.0f, voltage_limit);
    // 计算占空比
    // 限制占空比从0到1
    dc_a = _constrain(Ua / voltage_power_supply, 0.0f, 1.f);
    dc_b = _constrain(Ub / voltage_power_supply, 0.0f, 1.f);
    dc_c = _constrain(Uc / voltage_power_supply, 0.0f, 1.f);

    // 写入PWM到PWM 0,1,2通道
    ledcWrite(0, dc_a * 255); // 8位精度PWM, 范围0-255 (2^8-1)
    ledcWrite(1, dc_b * 255);
    ledcWrite(2, dc_c * 255);
}

如何理解占空比dc_a,b,c 限制到范围[0,1]，然后×255？

答：归一化到范围[0,1]是为了避免占空比溢出正常范围，因为可能受到环境干扰，会有一些Ua,Ub,Uc抖动值超过voltage_power_supply.

后面x255，类似于将RGB颜色各通道值限制到[0,1]范围后，再x255恢复至原来的[0,255]范围. [0,1]和[0,255]是RGB颜色的不同表现形式，前者更适合数学计算场景，后者更直观，x255是将[0,1]形式转换为[0,255]形式.

当然，这里x255并不是乱设的，而是由前面初始化时调用ledcSetup(0, 30000, 8)，将PWM通道占空比精度设为8，最多支持256个占空比等级，而非我们通常理解的100个等级（0%~100%）.

velocityOpenloop

velocityOpenloop实现：

img

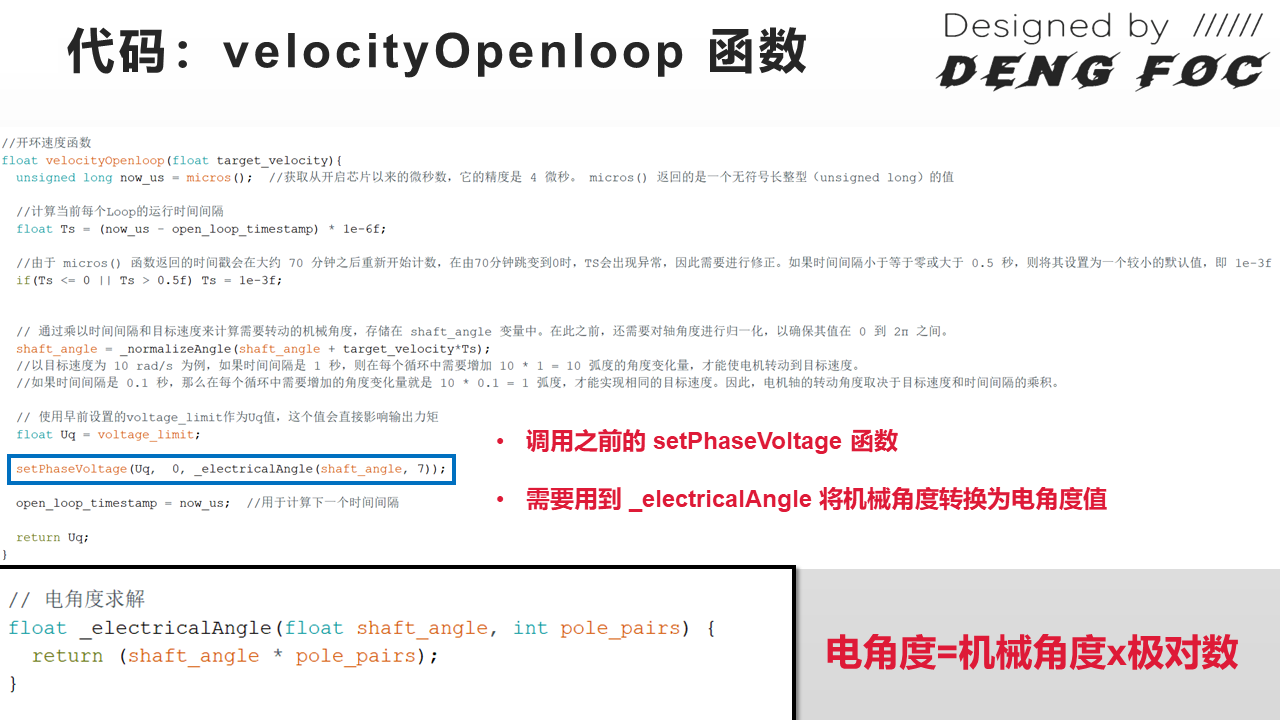
velocityOpenloop 负责接收用户输入的目标速度值，然后计算出Uq、电角度θ.

float voltage_limit = 10;
float shaft_angle = 0, open_loop_timestamp = 0;

// 开环速度函数
// target_velocity 目标速度(rad/s)
float velocityOpenloop(float target_velocity) {
    unsigned long now_us = micros(); // 获取从开启芯片以来的微秒数, 精度4us.

    // 计算当前每个Loop的运行时间间隔
    float Ts = (now_us - open_loop_timestamp) * 1e-6f;

    // 由于 micros() 函数返回的时间戳会在大约 70 分钟后重新开始计数, 在由70分钟跳变到0时, 
    // Ts会出现异常, 因此需要修正. 如果时间间隔 <= 0 或 > 0.5s, 则将其设置为一个较小默认值, 即1e-3f
    if (Ts <= 0 || Ts > 0.5f) Ts = 1e-3f;

    // 通过乘以时间间隔和目标速度来计算需要转动的机械角度, 存储在 shaft_angle 变量中
    // 在此之前, 还需要对轴角度归一化, 以确保其值在0-2π之间
    shaft_angle = _normalizeAngle(shaft_angle + target_velocity * Ts);
    // 以目标速度为 10 rad/s 为例, 如果时间间隔1s, 则在每个循环中需要增加 10 * 1 = 10 rad, 才能使得电机转动到目标速度
    // 如果时间间隔是 0.1s, 那么在每个循环中, 需要增加的角度变化量是 10 * 0.1 = 1 rad, 才能实现相同的目标速度. 
    // 因此, 电机轴的转动角度取决于目标速度和时间间隔的乘积

    // 使用早期设置的voltage_limit作为Uq值, 这个值会直接影响输出力矩
    float Uq = voltage_limit;

    setPhaseVoltage(Uq, 0, _electricalAngle(shaft_angle, 7));

    open_loop_timestamp = now_us;

    return Uq;
}

// 电角度求解
// 电角度 = 机械角度 x 极对数
float _electricalAngle(float shaft_angle, int pole_pairs) {
    return (shaft_angle * pole_pairs);
}

注意：定时器精度，是指硬件计时的精度（可靠性），不是表示精度，如now_us=1，表示1us，但可靠性是4us.

如何生成电角度\(θ\)？

分2步：

1）生成机械角度haft_angle

shaft_angle 描述了转子与定子因旋转而形成的角度差，即转子的位置信息（相对于定子）. 由于我们会在main函数中，不断循环调用velocityOpenloop，电机也会随着时间变化按期望的速度旋转，因此，

\[shaft\_angle = shaft\_angle + target\_velocity * Δt \]

其中，\(Δt\)是2次相邻计算shaft_angle的时间差，shaft_angle是机械角度，需要归一化到\([0,2π)\)范围内（否则，角度不确定）.

2）根据电角度与机械角度关系，求出电角度θ

电角度 = 机械角度 x 极对数

电角度与机械角度的关系

img

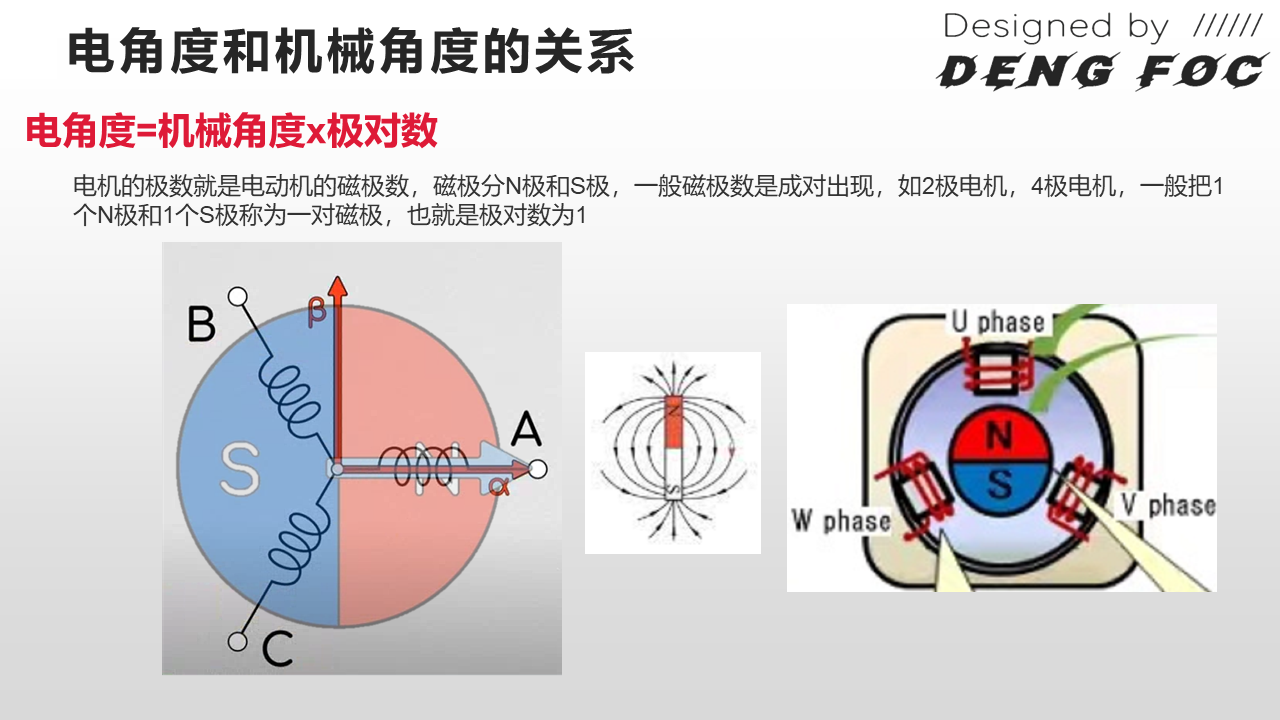
假设我们单独看\(U\)相，如果将电动机看作一个发电机，那么转子磁极N在磁场中旋转一圈，切割磁感线，再回到初始位置. 所发的电，就是一个发电周期，有正半轴、负半轴的部分（分别对应1个波峰、波谷）.

img

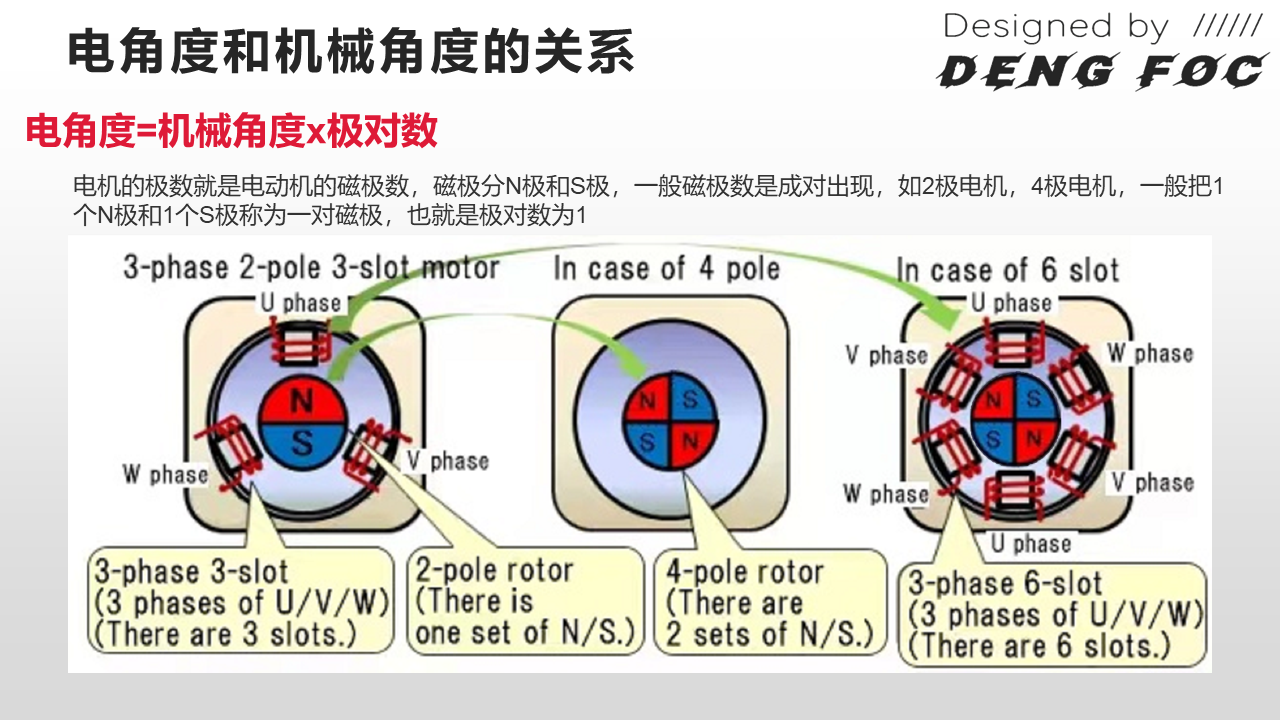
现在将磁极对扩展2，即有4个磁极. 那么，转子旋转一周，N极会产生2个发电周期.

同样地，磁极对为n时，转子旋转一周，N极会产生n个发电周期，对应n个相位周期.

也就是说，我们的转子选择一周，对应机械角度\(shaft\_angle=2π\)，产生了n个相位周期，我们将每个相位周期用电角度\(θ=2π\)来表示，n个相位周期，产生n个电角度周期. 就出现了电角度和机械角度对应关系：

电角度 = 机械角度 x 极对数

即：

\[θ=shaft\_angle\cdot n \]

其中，n是极对数.

初始化

//PWM输出引脚定义
int pwmA = 32;
int pwmB = 33;
int pwmC = 25;

//初始变量及函数定义
// 其他宏函数、全局变量
...
float zero_electric_angle=0, Ualpha, Ubeta=0, Ua=0, Ub=0, Uc=0, dc_a=0,dc_b=0,dc_c=0;

void setup() {
  Serial.begin(115200);
  
  //PWM设置
  pinMode(pwmA, OUTPUT);
  pinMode(pwmB, OUTPUT);
  pinMode(pwmC, OUTPUT);
  ledcAttachPin(pwmA, 0);
  ledcAttachPin(pwmB, 1);
  ledcAttachPin(pwmC, 2);
  ledcSetup(0, 30000, 8);  //pwm频道, 频率, 精度
  ledcSetup(1, 30000, 8);  //pwm频道, 频率, 精度
  ledcSetup(2, 30000, 8);  //pwm频道, 频率, 精度

  Serial.println("完成PWM初始化设置");
  delay(3000);
}

主循环

主循环很简单，

void loop() {
  // put your main code here, to run repeatedly:
   velocityOpenloop(5);
}

ESP32库函数

本文FOC实现用到了部分EPS32 Arduino 核心库函数，虽然不是FOC重点，但是涉及硬件控制，挑选部分重要函数讲解.

ledcSetup

ledcSetup 用于初始化 LEDC（LED PWM Control）硬件 PWM 通道，其任务是配置定时器频率、占空比分辨率，并绑定到指定通道

double ledcSetup(uint8_t channel, double freq, uint8_t resolution_bits);
  • channel：PWM 通道号（0~15）
  • freq：PWM 频率（单位：Hz）
  • resolution_bits：占空比分辨率位数（1~16，常用 8/10/12 位）

返回值：实际设置的频率（取决于具体硬件）

ledcSetup内部实现原理：

  1. 选择定时器和模式
  • channel 0-7确定用 高速模式，使用高速定时器（LEDC_HIGH_SPEED_MODE）；
  • channel 8-15确定用 低速模式，使用低速定时器（LEDC_LOW_SPEED_MODE）.
  1. 计算分频系数

根据输入的频率freq、分辨率resolution_bits，计算分频系数divider：

\[divider=\frac{APB\space clock(80MHz)}{freq \cdot (2^{resolution\_bits}-1)} \]

e.g. freq = 5000Hz, resolution_bits = 8, 那么\(divider = 80M/(5000-255)≈62.74\)，四舍五入取整63

  1. 配置定时器寄存器

设置定时器的分频系数和计数器位数

  1. 返回实际频率

因为计算分频系数时取整，所以实际频率与输入频率可能会存在误差

\[return \space clock = \frac{APB\space clock}{divider\cdot (2^{resolution\_bits}-1)} \]

e.g. divider = 63，那么实际频率 \(= 80M/(63\cdot 255)≈4993Hz\)

ledcWrite

ledcWrite 用于调节PWM占空比，其任务是控制LED亮度、电机速度等. 需要先调用ledcSetup初始化配置.

ledcWrite简化版实现：

void ledcWrite(uint8_t channel, uint32_t duty) {
    // 1. 检查通道有效性
    if (channel >= LEDC_CHANNEL_MAX) return;

    // 2. 获取通道对应的寄存器地址
    volatile uint32_t *duty_reg = &LEDC_DUTY_REG(channel);

    // 3. 写入占空比值（硬件自动生效）
    *duty_reg = duty << LEDC_DUTY_SHIFT;  // 根据分辨率左移对齐
}

其中，LEDC_DUTY_SHIFT在初始化时，调用ledcSetup会设置其值

FOC闭环位置

闭环位置控制的原理

img

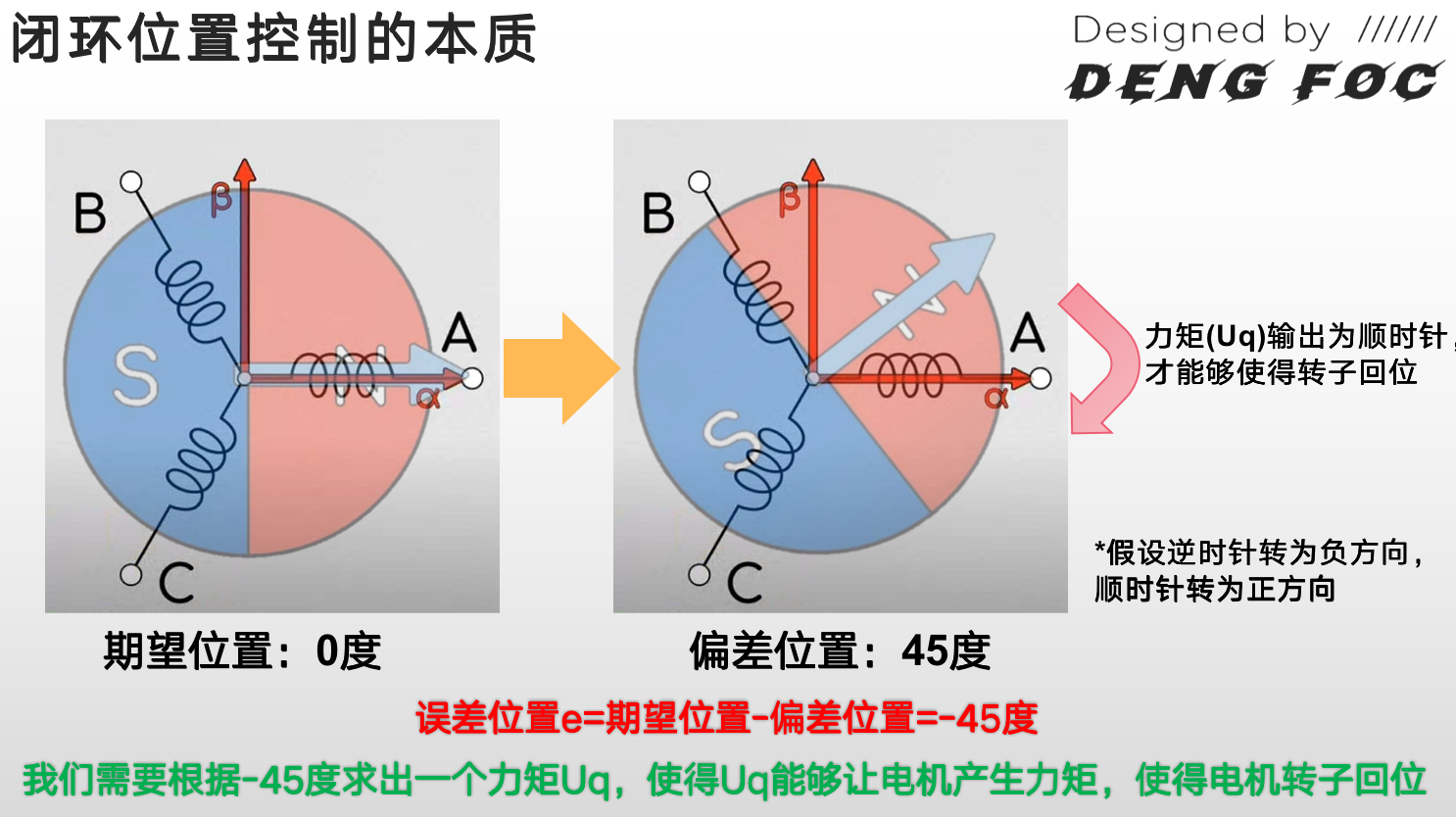
当电机转子位置（如偏差位置45°）并非期望位置（0°）时，即转子因旋转与定子形成一定夹角，我们需要控制电机产生一个力矩，让转子回到初始位置. 力矩跟Uq是等效的，要产生力矩，我们需要给一个合适的Uq，让电机回到0位.

所谓闭环位置控制，就是解决如何检测该角度偏差，怎么产生合适的旋转力矩Uq的问题.

假设逆时针方向旋转为负方向，顺时针旋转为正方向. 电机误差位置用e表示，所以，误差位置计算：

\[误差位置e=期望位置-偏差位置=-45° \]

问题转换为：根据偏差位置（如45°）求出力矩Uq，使得Uq让电机产生力矩，从而让转子回到0位置.

如何将误差位置e转换成Uq值？

以车载12V供电系统为例，驱动电机电源电压12V，于是，Uq的变化范围Uqmax=±6V. 想让电机在45°偏差时，产生最大回正力矩，那么该系数为：

\[K_p=|Uqmax|÷|±45|=6÷45=0.133 \]

于是，可计算出当电机处于误差位置e时，需要让电机回正所需要的力矩Uq：

\[Uq=Kp\cdot e\xrightarrow{if \space e=-45°}Uq=0.133\cdot (-45°)=-5.985V \]

这个Kp就是PID控制中的P环系数.

式子中，\(Kp\)可用最大力矩的限制计算得到，而误差位置e可通过编码器（如as5600）测量转子角度得到.

下图是PID位置控制器示意图：

这里的闭环位置控制，处于简单考虑，只用了P环，没有用I环、D环.

img

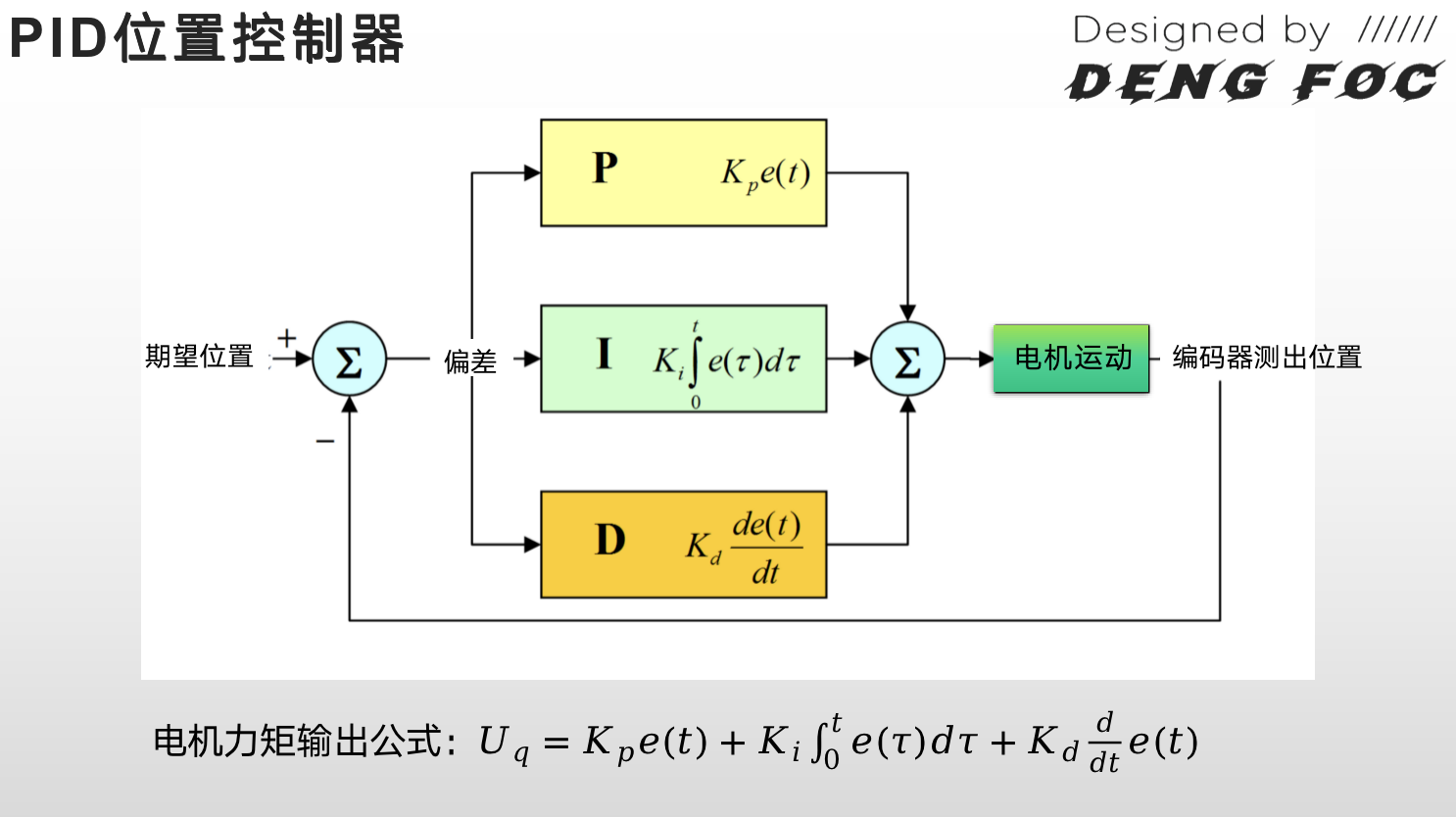
闭环位置控制的整个过程可以总结为：

img

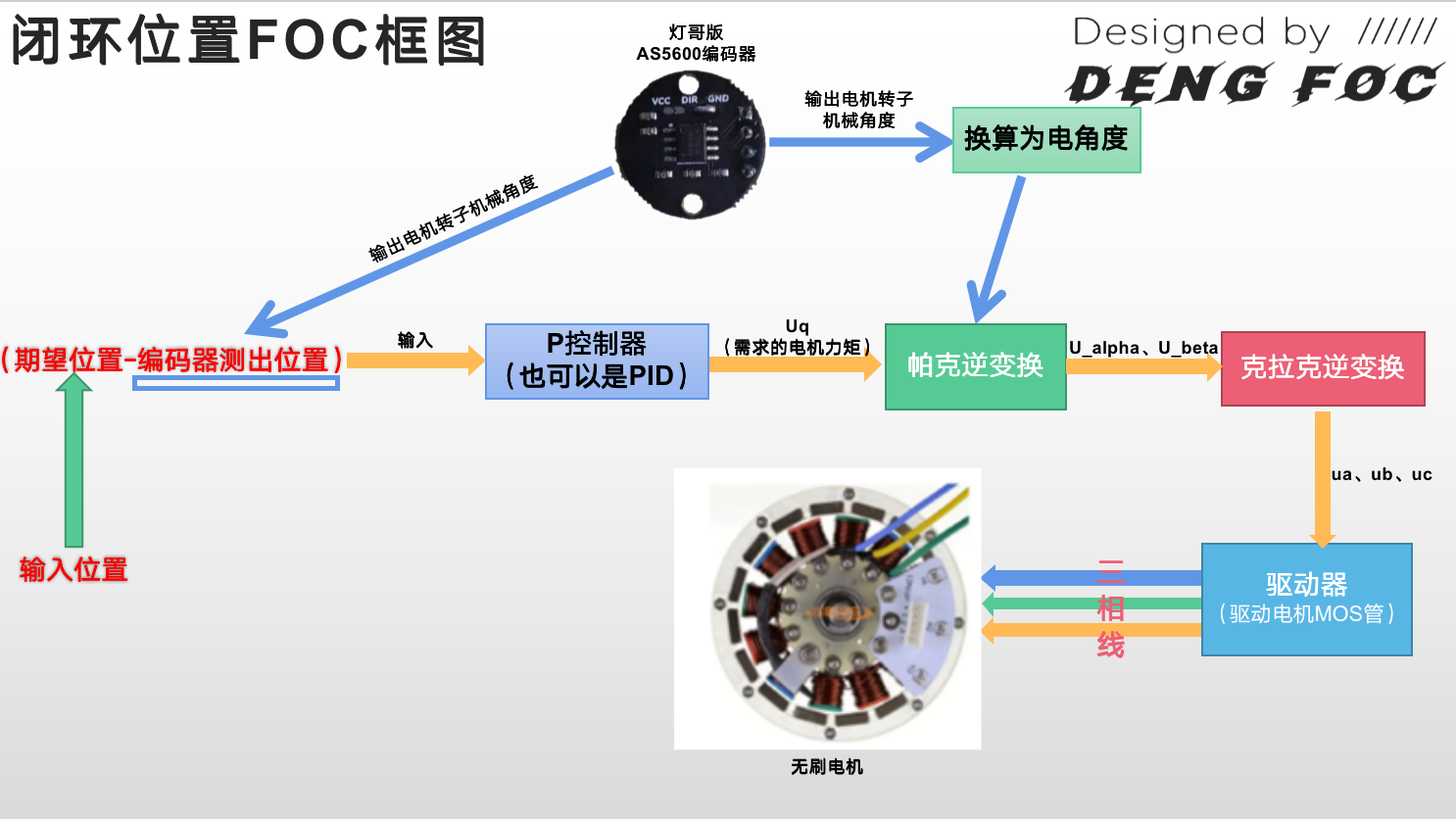
实现位置闭环有多种方式，常见有：

  • 方式1：位置-力控制，通过控制力矩实现位置闭环
  • 方式2：位置-速度-力控制，通过控制力矩、速度，实现位置闭环

闭环位置控制代码编写

在开环速度控制代码基础上，实现方式2的位置闭环.

从编码器读取角度

从编码器读取角度，分为3种类型：

1）从编码器读取原始的角度值，MCU通过i2c与编码器通信
2）将从编码器读取的角度值，转换为弧度值
3）累积从编码器读取的角度值，用圈数 + 读取的角度值

int _raw_ang_hi = 0x0c;
int _raw_ang_lo = 0x0d;
int _ams5600_Address = 0x36;
...
int full_rotations = 0; // 软件实现圈数累计
float angle_prev = 0;   // 上一次读取的角度值

// 从编码器读取的原始角度值
word getRawAngle() {
    return readTwoBytes(_raw_ang_hi, _raw_ang_lo);
}

// 读取单圈的角度值(不累计)
float getAngle_Without_track() {
    return getRawAngle() * 0.08789 * M_PI / 180; // 角度 => 弧度
}

// 读取累计角度值(累计圈数)
float getAngle() {
    float val = getAngle_Without_track();
    float d_angle = val - angle_prev;

    // 计算旋转的总圈数
    // 通过判断角度变化是否大于一圈的80%(0.8*2π ≈ 0.8f * 6.28318530718f)判断是否发生溢出,
    // 如果发生溢出, 则full_rotations-1（如果d_angle > 0）；否则, full_rotations+1.
    if (abs(d_angle) > (0.8f * 6.28318530718f) )
        full_rotations += ( d_angle > 0) ? -1 : 1;
    angle_prev = val;
    return (float)full_rotations * 6.28318530718f + angle_prev;
}

// 从I2C设备(编码器)读取2byte数据, 并合并成16 bits数据作为角度值. 具体方式取决于所用编码器
// in_adr_hi: 高字节数据地址
// in_adr_lo: 低字节数据地址
// 返回读取的角度值
word readTwoBytes(int in_adr_hi, int in_adr_lo)
{
  word retVal = -1;
 
  /* 读低位 */
  Wire.beginTransmission(_ams5600_Address);
  Wire.write(in_adr_lo);
  Wire.endTransmission();
  Wire.requestFrom(_ams5600_Address, 1);
  while(Wire.available() == 0);
  int low = Wire.read();
 
  /* 读高位 */  
  Wire.beginTransmission(_ams5600_Address);
  Wire.write(in_adr_hi);
  Wire.endTransmission();
  Wire.requestFrom(_ams5600_Address, 1);
  while(Wire.available() == 0);
  int high = Wire.read();
  
  retVal = (high << 8) | low;
  
  return retVal;
}

计算电角度

读取机械角度，用以计算电角度时，使用的是真实的机械角度getAngle_Without_track()，而不用软件累计的角度getAngle().

开环速度控制提到，电角度 = 机械角度 x 极对数.
这里求电角度时，为什么将 DIR * 极对数(PP) * 机械角度

// 电角度求解
float _electricalAngle() {
    return _normalizeAngle((float)(DIR * PP) * getAngle_Without_track() - zero_electric_angle);
}

(DIR * PP) * getAngle_Without_track() 就是计算出来的电角度，通常与真是电角度有偏差；

zero_electric_angle 是电角度0位偏差. 通常测出来电角度会与真实电角度有一个偏差，zero_electric_angle就是这个偏差值. 可通过初始化时0位偏差进行校准.

校准过程：

void setup() {
    ...
    // 通过0位偏差, 校准电角度
    setPhaseVoltage(3, 0, _3PI_2);
    delay(3000);
    zero_electric_angle = _electricalAngle();
    setPhaseVoltage(0, 0, _3PI_2);
    ...
}

主循环

void loop() {
    Serial.println(getAngle());
    float Sensor_Angle = getAngle();
    float Kp = 0.133; // Kp=|Uqmax|÷|±45|
    // Uq = Kp * e
    setPhaseVoltage(_constrain(Kp * (motor_target - DIR * Sensor_Angle) * 180 / M_PI, -6, 6), 0, _electricalAngle());
    serialReceiveUserCommand(); // 从串口接收用户输入的 目标位置值, 会写入motor_target
}

motor_target - DIR * Sensor_Angle就是误差位置e；DIR 编码器方向，需要实测得到.

serialReceiveUserCommand()从串口接收用户输入的 目标位置值，写入全局变量motor_target.

为什么要用_constrain将Kp*e限制在[-6,6]之间？

前面讲过，Uqmax=±6V，Uq的最大变化范围就是[-6,6]. 如果不加以限制，Uq超限，电机可能会卡顿，导致不正常旋转.

为什么读取传感器角度Sensor_Angle用getAngle()，而不是用getAngle_Without_track()？

因为这里为了计算 误差位置e = 期望位置 - 偏差位置，其中，期望位置由用户输入（motor_target），偏差位置是转子从初始位置顺时针旋转到定子位置所需的角度. 实际偏转位置，可能是用户（负载）导致转子旋转而形成的角度差，可能超过一圈，因此需要考虑累积角度.

完整代码参见：5 FOC闭环位置代码的撰写

FOC闭环速度

可以单独控制速度，也可以作为“闭环位置原理”中，方式2 的位置闭环：位置-速度-力闭环的中间环节

如下图，是闭环位置框图，可通过编码器测出转子位置：

img

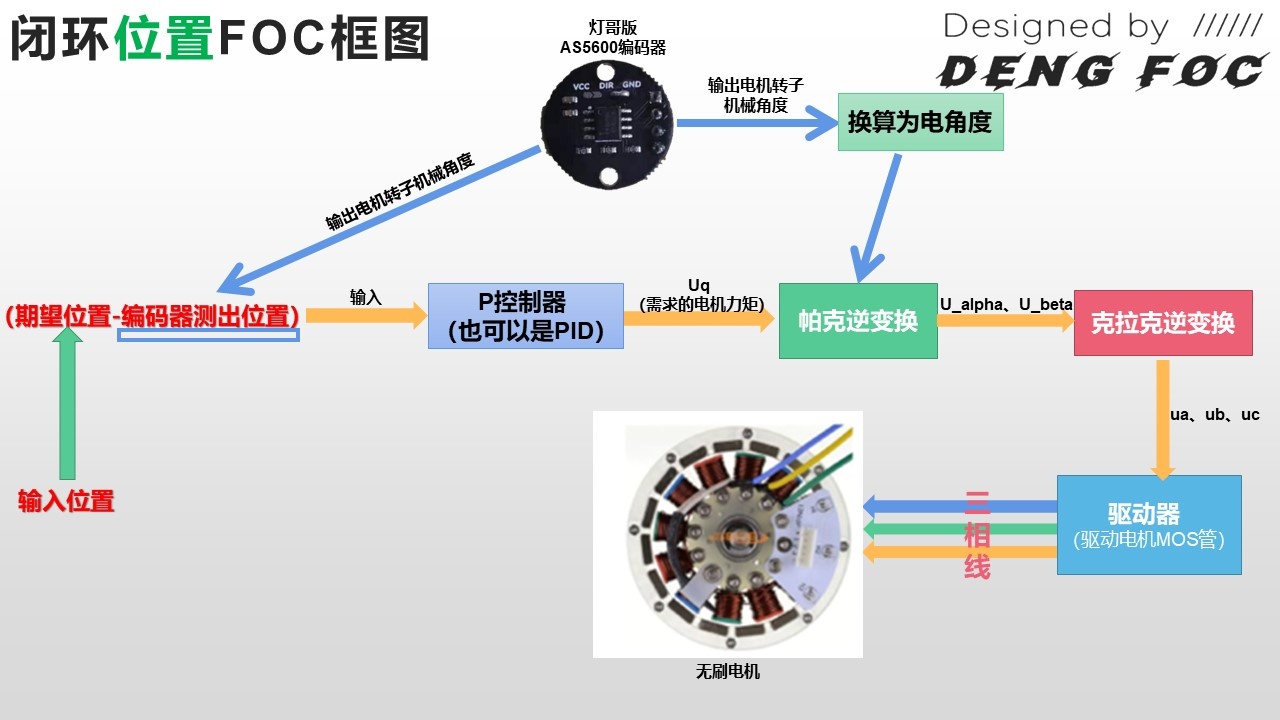
如果用方式2的位置闭环：位置-速度-力闭环，用到了速度闭环算法.

使用速度环，需要解决的问题：

1）如何用编码器获取电机转子速度？

2）为何对速度值进行滤波？如何滤波？

3）为什么用PI控制器对速度环进行控制？有什么效果？

通过编码器获取转子速度，经低通滤波器后，得到编码器测出速度.

获取速度

\[误差速度e = 期望速度 - 最终测量速度\\ \iff error=target\_velocity - velocity \]

其中，期望速度由用户输入，测量速度由编码器采集到的角度值，经过计算、低通滤波得到.

编码器得到的测量速度（未滤波）：

\[测量速度 = (编码器获取角度 - 上一次获取角度)/dt\\ \iff sensor.velocity = (angle\_prev - angle) \]

从编码器获取角度时，我们用的是累计了圈数的角度. 计算得来的测量速度，其实是角速度.

在获取编码器角度时，由于编码器角度在0.6~6.28(2*3.14=6.28)之间循环，也就是说，我们无法通过 角度变化 > 2π，来判断圈数+1；具体需要 角度变化 > ?，才能判断圈数+1，需要结合实际测量数据得出.

这里，我们采用 角度变化 > 0.8 * 360°，判断圈数+1

img

主要代码如下：

float angle_prev           = 0; // 最后一次调用getSensorAngle()的结果，用于得到完整的圈数和速度
long angle_prev_ts         = 0; // 上次调用 getAngle 的时间戳
float vel_angle_prev       = 0; // 最后一次调用 getVelocity 时的角度
long vel_angle_prev_ts     = 0; // 最后速度计算时间戳
int32_t full_rotations     = 0; // 总圈数计数
int32_t vel_full_rotations = 0; //用于速度计算的先前完整旋转圈数

float Sensor_AS5600::getVelocity() {
    // 计算采样时间
    float Ts = (angle_prev_ts - vel_angle_prev_ts)*1e-6;
    // 快速修复奇怪的情况（微溢出）
    if(Ts <= 0) Ts = 1e-3f;
    // 速度计算
    float vel = ( (float)(full_rotations - vel_full_rotations)*_2PI + (angle_prev - vel_angle_prev) ) / Ts;    
    // 保存变量以待将来使用
    vel_angle_prev = angle_prev;
    vel_full_rotations = full_rotations;
    vel_angle_prev_ts = angle_prev_ts;
    return vel;
}

// 计算圈数
void Sensor_AS5600::Sensor_update() {
    float val = getSensorAngle(); // 从传感器直接读取角度值
    angle_prev_ts = micros();
    float d_angle = val - angle_prev;
    // 圈数检测
    if(abs(d_angle) > (0.8f*_2PI) ) full_rotations += ( d_angle > 0 ) ? -1 : 1; 
    angle_prev = val;
}

速度的低通滤波

滤波原理：
数学角度看，就是一个线性插值公式（参见解析几何笔记：仿射坐标系）

\[最终测量速度 = 上一次最终测量速度 * α + 本次测量速度 * (1-α)\\ \iff velocity\_filter = velocity\_filter\_prev \cdot α + sensor.velocity \cdot (1-α) \]

其中，

  • 滤波后的速度，就是最终测量速度；
  • 平滑因子α

\(α=alpha = T_f / (T_f + dt)\) ，基于指数衰减滤波器. 公式目的：根据时间常数\(T_f\)、时间间隔\(dt\)的比例来控制滤波器对当前输入信号和前一次滤波结果的加权比例.

时间常数\(T_f\)由开发者决定，它与dt关系：

1）当\(dt \ll T_f\)时，\(α≈1\)，滤波器主要依赖于前一次滤波结果，当前输入信号的影响足够小；

2）当\(dt \gg T_f\)时，\(α≈0\)，滤波器主要依赖于当前输入信号，前次滤波结果影响较小

主要代码如下：

float Tf = time_constant;                 //!< 低通滤波时间常数
unsigned long timestamp_prev = micros();  //!< 最后执行时间戳
float y_prev = 0.0f;                      //!< 上一个循环中的过滤后的值

float LowPassFilter::operator() (float x)
{
    unsigned long timestamp = micros();
    float dt = (timestamp - timestamp_prev)*1e-6f;

    if (dt < 0.0f ) dt = 1e-3f;
    else if(dt > 0.3f) {
        y_prev = x;
        timestamp_prev = timestamp;
        return x;
    }

    float alpha = Tf / (Tf + dt);
    float y = alpha * y_prev + (1.0f - alpha) * x;
    y_prev = y;
    timestamp_prev = timestamp;
    return y;
}

//无滤波
float DFOC_M0_Velocity_WithoutFilter()
{
    return DIR * S0.getVelocity();
}

//有滤波
float DFOC_M0_Velocity()
{
    //获取速度数据并滤波
    float vel_M0_ori  = S0.getVelocity();
    float vel_M0_flit = M0_Vel_Flt(DIR*vel_M0_ori);
    return vel_M0_flit;   //考虑方向
}

速度的PI控制

整体流程与闭环位置类似，不过我们这次处理输入时，使用PI控制器，而不用单独的P控制器.

PID控制（离散形式）：

\[output = Kp * e_k + Ki * ∑_{i=0}^ke_iΔt + Kd * \frac{e_k-e_{k-1}}{Δt} \]

其中，\(e_k\)就是我们所说的error，

\[error=target\_velocity - sensor.velocity \]

对于PI控制器，我们忽略微分项.

为什么要使用PI控制器，而不用P控制器？

因为单独的速度环P控制器有缺陷. 如果只有P环，对于有负载和无负载的情形，P环只会根据 速度误差 输出相同力矩，导致无负载的更快达到目标速度；但是，我们希望有负载时能增大力矩，从而提高达到目标速度的效率.

如果e(t)长时间没有被P环调节过来，I环积分就会不断增大e(t)，使得电机的输出力越来越大，让电机实现更快的纠偏.

img

主要代码如下：

// 构造函数
PIDController::PIDController(float P, float I, float D, float ramp, float limit)
    : P(P)
    , I(I)
    , D(D)
    , output_ramp(ramp)    // PID控制器加速度限幅, 受控对象的输出斜率
    , limit(limit)         // PID控制器输出限幅
    , error_prev(0.0f)
    , output_prev(0.0f)
    , integral_prev(0.0f)
{
    timestamp_prev = micros();
}

float PIDController::operator() (float error){
    // 计算两次循环中间的间隔时间
    unsigned long timestamp_now = micros();
    float Ts = (timestamp_now - timestamp_prev) * 1e-6f;
    if(Ts <= 0 || Ts > 0.5f) Ts = 1e-3f;
    
    // P环
    float proportional = P * error;
    // Tustin 散点积分（I环）
    float integral = integral_prev + I*Ts*0.5f*(error + error_prev);
    integral = _constrain(integral, -limit, limit);
    // D环（微分环节）
    float derivative = D*(error - error_prev)/Ts;

    // 将P,I,D三环的计算值加起来
    float output = proportional + integral + derivative;
    output = _constrain(output, -limit, limit);

    if(output_ramp > 0){
        // 对PID的变化速率进行限制
        float output_rate = (output - output_prev)/Ts;
        if (output_rate > output_ramp)
            output = output_prev + output_ramp*Ts;
        else if (output_rate < -output_ramp)
            output = output_prev - output_ramp*Ts;
    }
    // 保存值（为了下一次循环）
    integral_prev = integral;
    output_prev = output;
    error_prev = error;
    timestamp_prev = timestamp_now;
    return output;
}

为什么计算积分项integral时，要用integral_prev + I*Ts*0.5f*(error + error_prev)？

答：积分项本质是计算从系统启动（0时刻）到目前为止的累积误差，相当于求error-t曲线与t轴围成的区域面积，每一个Ts时间宽度对应的面积，可看成一个梯形，error和error_prev就是梯形的高，因此，

\[梯形面积 = 0.5 * Ts * (error + error\_prev) \]

那么，对于I项，

\[\begin{aligned} integral &= \sum_{i=0}^k梯形面积 + 本次梯形面积 \\ &= error\_prev+0.5 * Ts * (error + error_prev) \end{aligned} \]

为什么用output_ramp限制PID输出值的变化率？

答：output_ramp是由调用者设置的，用来限制PID输出值的斜率，用于避免输出值太太从而导致系统振荡.

输出值斜率计算：

\[output\_rate = (output - output\_prev) / dt ; \]

速度闭环

用户传入P、I参数，经由PID控制器（PIDController）根据误差速度，计算出PID输出值，将其作为Uq，与电角度一起传入setTorque，从而计算出Ua, Ub, Uc值，并控制产生对应占空比的PWM波形.

// PID
PIDController vel_loop_M0 = PIDController{.P = 2, .I = 0, .D = 0, .ramp = 100000, .limit = voltage_power_supply/2};

//=================PID 设置函数=================
//速度PID
void DFOC_M0_SET_VEL_PID(float P, float I, float D, float ramp)   //M0角度环PID设置
{
    vel_loop_M0.P=P;
    vel_loop_M0.I=I;
    vel_loop_M0.D=D;
    vel_loop_M0.output_ramp=ramp;
}

// M0速度PID接口
float DFOC_M0_VEL_PID(float error)   //M0速度环
{
    return vel_loop_M0(error);
}

// ====== User Interface =======
void DFOC_M0_setVelocity(float Target)
{
    setTorque(DFOC_M0_VEL_PID((serial_motor_target() - DFOC_M0_Velocity()) * 180 / PI), _electricalAngle());   //速度闭环
}


void loop()
{
    // 设置速度环PID参数
    DFOC_M0_SET_VEL_PID(0.005, 0.00, 0,0);
    // 设置目标速度
    DFOC_M0_setVelocity(serial_motor_target());
    ...
}

位置闭环

类似于速度闭环，

PIDController angle_loop_M0 = PIDController{ .P = 2, .I = 0, .D = 0, .ramp = 100000, .limit = 100 };

//角度PID
void DFOC_M0_SET_ANGLE_PID(float P,float I,float D,float ramp)   //M0角度环PID设置
{
  angle_loop_M0.P=P;
  angle_loop_M0.I=I;
  angle_loop_M0.D=D;
  angle_loop_M0.output_ramp=ramp;
}

//M0角度PID接口
float DFOC_M0_ANGLE_PID(float error)
{
  return angle_loop_M0(error);
}

// ====== User Interface =======
void DFOC_M0_set_Velocity_Angle(float Target)
{
    setTorque(DFOC_M0_VEL_PID(DFOC_M0_ANGLE_PID((Target - DFOC_M0_Angle()) * 180 / PI)), _electricalAngle());   //角度闭环
}

// 本质是前面讲的位置闭环
void DFOC_M0_set_Force_Angle(float Target)   //力位
{
    setTorque(DFOC_M0_ANGLE_PID((Target-DFOC_M0_Angle()) * 180 / PI), _electricalAngle());
}

设置力矩

因为力矩等效于相电压(Ua,Ub,Uc)，所以设置力矩setTorque其实就是在设置相电压. 因此，setTorque的内容，与前面的setPhaseVoltage基本一致.

不同点：
1）对角度的处理，setTorque需要先更新传感器数据，进行圈数判定；setPhaseVoltage没有这一步；
2）setTorque内置Ud=0，setPhaseVoltage由用户传入.

// 设置力矩 <=> 设置相电压
void setTorque(float Uq, float angle_el) {
    S0.Sensor_update(); //更新传感器数值
    Uq       = _constrain(Uq, -(voltage_power_supply)/2, (voltage_power_supply)/2);
    float Ud = 0;
    angle_el = _normalizeAngle(angle_el);

    // 帕克逆变换
    Ualpha = -Uq * sin(angle_el); 
    Ubeta  =  Uq * cos(angle_el); 

    // 克拉克逆变换
    Ua = Ualpha + voltage_power_supply / 2;
    Ub = (sqrt(3) * Ubeta - Ualpha) / 2 + voltage_power_supply / 2;
    Uc = (-Ualpha - sqrt(3) * Ubeta) / 2 + voltage_power_supply / 2;
    setPwm(Ua, Ub, Uc);
}

初始化与主循环

主循环中，可以设置目标速度，或者改成想要控制的目标是速度 or 位置.

int Sensor_DIR = -1;    // 传感器方向
int Motor_PP   =  7;    // 电机极对数

void setup() {
    Serial.begin(115200);
    DFOC_Vbus(12.6);   // 设定驱动器供电电压
    DFOC_alignSensor(Motor_PP,Sensor_DIR);
}

void loop() 
{
    // 设置速度环PID参数
    DFOC_M0_SET_VEL_PID(0.005, 0.00, 0,0);
    // 设置目标速度
    DFOC_M0_setVelocity(serial_motor_target());
    // 接收串口
    serialReceiveUserCommand();
}

FOC闭环电流

通常，FOC环节涉及3个环：速度环、位置环、电流环.

之前，FOC力矩环是通过设置Uq实现电机力矩输出，因为没有传感器检测电机力矩，因此FOC力矩环是开环的.

要进一步精确控制电机，就需要对力矩进行精确的闭环控制. 电流传感器的电流输出，经过换算后，可以转换成力矩值，因此，可用反馈的电流求出电机力矩，进行力矩闭环.

原理

q轴电流\(Iq\)一定程度上能代表电机力矩，只需要电机的KV值，就能将\(I_q\)转换成电机力矩：

\[Torque [N\cdot m] = 8.27 * I_q [A] / KV \]

电机的KV值是直流电机（尤其无刷电机）的一个重要参数，表示电机在空载状态下，每伏特（V）电压对应的转速（RPM），单位为 RPM/V. 反映了电机的速度特性，是选型和控制的关键指标之一.

想控制力矩，只需要控制检测出来的电流值\(I_q\)达到我们设定的期望值\(I\_q\_ref\) 即可.

类似于速度闭环，我们可以用PID算法对电流闭环，从而实现力矩闭环：

\[Uq = PID(I\_q\_ref - I\_q) \]

其中，\(I\_q\)是q轴电流（即观测力矩），\(I\_q\_ref\)是我们期望的q轴电流（即期望力矩）. 经过PID算法后，能输出对电机进行控制的Uq值.

1）当\(I\_q\_ref - I\_q < 0\)时，实际力矩 > 期望力矩，此时Uq会变小；

2）当\(I\_q\_ref - I\_q > 0\)时，实际力矩 < 期望力矩，此时Uq会变大.

在有反馈的情况下（PID），电机能稳定在设定的力矩中. 这就是电流闭环原理.

而根据前面的克拉克变换，可以将\(i_a,i_b,i_c\)转化成\(i_α,i_β\)（等幅值形式）：

\[\begin{cases} i_α = i_a\\ i_β = \frac{1}{\sqrt 3}(2i_b+i_a) \end{cases} \]

再由帕克变换，可将\(i_α,i_β\)转换成\(i_q,i_d\)：

\[\begin{bmatrix} i_q\\ i_d \end{bmatrix} = R(-θ,z)\begin{bmatrix} i_α\\i_β \end{bmatrix} =\begin{bmatrix} cosθ & sinθ\\ -sinθ & cosθ \end{bmatrix} \begin{bmatrix} i_α\\i_β \end{bmatrix} \]

于是，如何测量\(i_q,i_d\)，转化成如何测量\(i_a,i_b,i_c\).
再由基尔霍夫电流定律，\(i_a+i_b+i_c=0\)，我们只需要测量其中2相电流，即可得到\(i_q\)

如何测量A、B、C相电流？

img

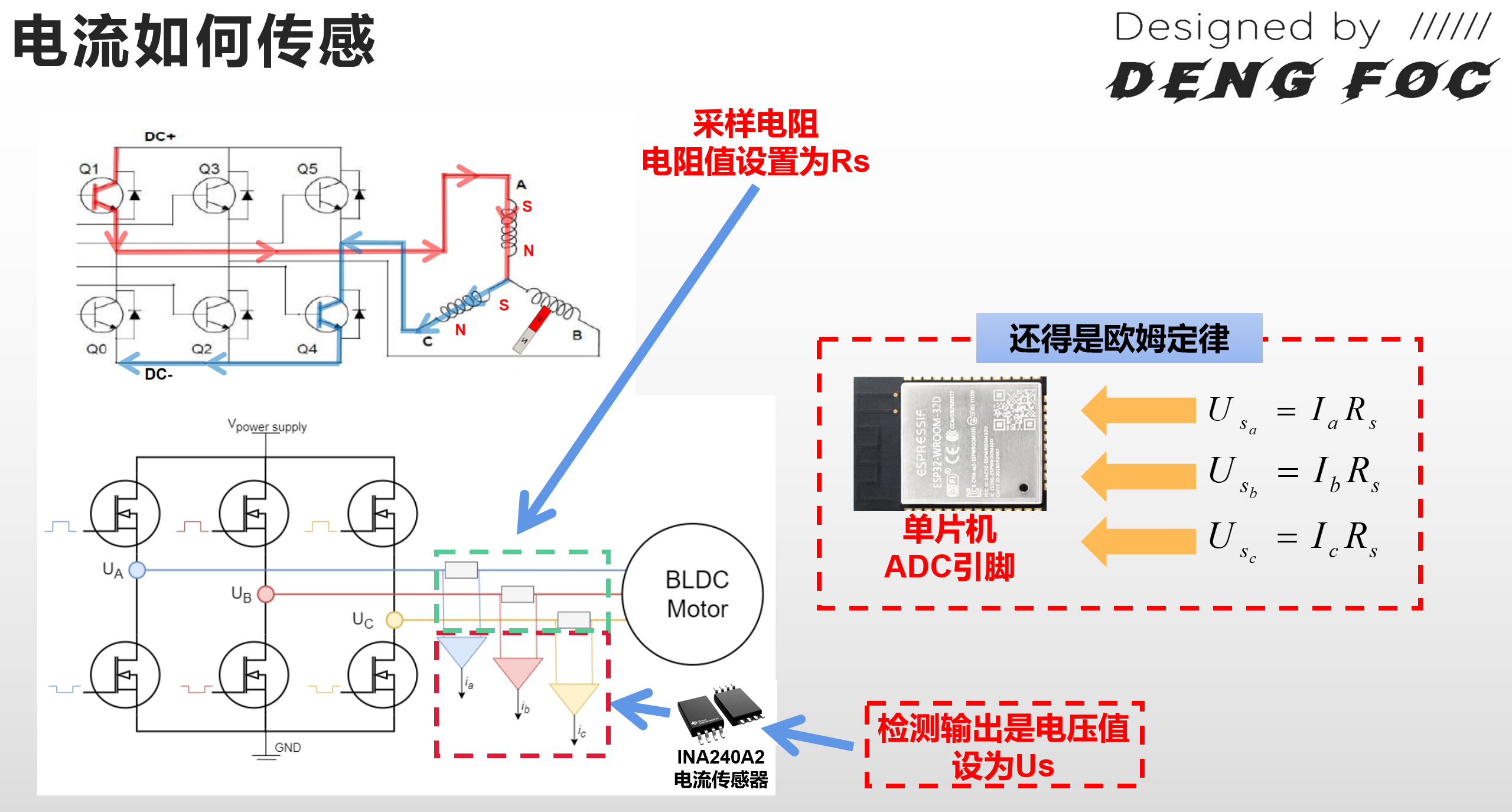
答：可以利用欧姆定律，在A、B、C这3相回路上分别串联3个等值小电阻\(R_s\)、接入一个电流传感器（如INA240A2）. 当相线中有电流经过时，传感器就能采集到电阻2端电压值，MCU读取这个电压值后，除以\(R_s\)，就能得到相电流.

\[i_a = \frac{U_{S_a}}{R_s}\\ i_b = \frac{U_{S_b}}{R_s}\\ i_c = \frac{U_{S_c}}{R_s} \]

闭环电流代码编写

电流采集

电路中，采样电阻\(R_s=0.01Ω\)

∵电流传感器INA240A2将检测到的电流放大了50倍（amp_gain=50）
∴真实电流：

\[I=\frac{U}{amp\_gain \cdot R_s} \]

float _shunt_resistor = 0.01; // Rs, unit: Ω

volts_to_amps_ratio = 1.0f /_shunt_resistor / amp_gain; // 将电压转化为电流
gain_a = volts_to_amps_ratio * (-1);
gain_b = volts_to_amps_ratio * (-1);
gain_c = volts_to_amps_ratio;
// 电流读取
current_a = (readADCVoltageInline(pinA) - offset_ia) * gain_a; // unit: A
current_b = (readADCVoltageInline(pinB) - offset_ib) * gain_b; // unit: A
current_c = (!_isset(pinC)) ? 0 : (readADCVoltageInline(pinC) - offset_ic)*gain_c; // unit: A

∵电流传感器的方向都是负方向
∴需要根据实际情况规整\(i_a,i_b,i_c\)的方向，volts_to_amps_ratio乘以-1，就是将电流反向.

电流ADC转换

readADCVoltageInline是从电流传感器读取的ADC值，代表电阻两端电压值. 当读取到ADC值后，需要将其换算成电阻电压. 具体的换算方法，取决于ADC电压、分辨率，实现如下：

#define _ADC_VOLTAGE 3.3f            //ADC 电压
#define _ADC_RESOLUTION 4095.0f      //ADC 分辨率

// ADC 计数到电压转换比率求解
#define _ADC_CONV ( (_ADC_VOLTAGE) / (_ADC_RESOLUTION) )

float CurrSense::readADCVoltageInline(const int pinA){
  uint32_t raw_adc = analogRead(pinA);
  return raw_adc * _ADC_CONV;
}

0点漂移

offset_ia, offset_ib 代表A、B相电流传感器的0点漂移，电流传感器不是理想器件，存在0点漂移. 在计算真实电压时，需要消除0点漂移.

current_a = (readADCVoltageInline(pinA) - offset_ia) * gain_a;

如何求得0点漂移值offset_ia, offset_ib呢？

上电后，初始化时，可读取电流传感器的电压值1000遍，然后求平均得到就是0点漂移：

// 查找 ADC 零偏移量的函数
void CurrSense::calibrateOffsets(){
    const int calibration_rounds = 1000;

    // 查找0电流时候的电压
    offset_ia = 0;
    offset_ib = 0;
    offset_ic = 0;
    // 读数1000次
    for (int i = 0; i < calibration_rounds; i++) {
        offset_ia += readADCVoltageInline(pinA);
        offset_ib += readADCVoltageInline(pinB);
        if(_isset(pinC)) offset_ic += readADCVoltageInline(pinC);
        delay(1);
    }
    // 求平均，得到误差
    offset_ia = offset_ia / calibration_rounds;
    offset_ib = offset_ib / calibration_rounds;
    if(_isset(pinC)) offset_ic = offset_ic / calibration_rounds;
}

电流闭环

类似于速度闭环，电流闭环也是使用PI控制器（D项为0）.

PIDController current_loop_M0 = PIDController{.P = 1.2, .I = 0, .D = 0, .ramp = 100000, .limit = 12.6};

void DFOC_M0_SET_CURRENT_PID(float P,float I,float D,float ramp)    //M0电流环PID设置
{
    current_loop_M0.P=P;
    current_loop_M0.I=I;
    current_loop_M0.D=D;
    current_loop_M0.output_ramp=ramp;
}

void DFOC_M0_setTorque(float Target)            //电流力矩环
{
    setTorque(current_loop_M0(Target-DFOC_M0_Current()),_electricalAngle());
}

void runFOC()
{
    //====传感器更新====
    S0.Sensor_update();
    CS_M0.getPhaseCurrents();

    //====传感器更新====
}

int counter = 0;
void loop()
{
    runFoc();
    DFOC_M0_SET_CURRENT_PID(5, 200, 100000);
    DFOC_M0_setTorque(serial_motor_target());
    counter++;
    if (counter > 30) {
        counter = 0;
        Serial.printf("%f\n", DFOC_M0_Current());
    }
    // 接收串口
    serialReceiveUserCommand();
}

参考

DENG FOC文档

posted @ 2025-07-20 19:33  明明1109  阅读(1520)  评论(1)    收藏  举报