[总结]一些 DP 优化方法

目录

写在前面

  1. ACM 训练（复习）的时候重新学习了一下常见的 DP 转移的优化技巧，在学习的同时也有一些自己的理解，便一并总结在这。
  2. 本文成文前阅读或参照了许多大佬的博客，这些将附在文末参考文献中。
  3. 若文章中出现错误，烦请告知。感谢您的造访。

矩阵快速幂优化

主要是利用矩阵快速幂来优化一些线性递推问题。高维 DP 如果某一维状态较少也可以用矩乘优化。

这个比较普及不细讲，但是注意图的邻接矩阵也是可以用来矩阵加速的。

例题

前缀和优化

当转移碰到类似于 $f_i=\sum\limits_{l\leq j\leq r}g_j$ 时，我们可以对 $g$ 做一个前缀和，之后两端点差分即可。同时，其中求和式可换成 $\min$ 或 $\max$，不过优化的适用条件更为苛刻。

另外多维 DP 有时也能用到前缀和优化，关键就是找到转移式有哪一个部分是只随着一个枚举变量变化而变化的，通过交换枚举顺序可以做到用前缀和优化。另外，要注意取的究竟是“前缀”还是“后缀”或是中间某两个端点，计算端点的值的时候要考虑交换 for 对循环范围的影响。[HEOI 2013]SAO这题可能会让你对这部分有充分了解。

例题

two-pointer 优化

也就是双指针优化。最常见的双指针优化是“尺取法”。双指针优化，大概就是一个端点移动时，取最优值时另一个端点是单调移动的。

例如，我想在一个有序数组 $a$ 中找到两个数 $a_i,a_j(i<j)$，使得 $a_j-a_i\leq C$ 且 $a_j-a_i$ 最大。那么我们移动左端点 $i$ 时，只需找到 $a_j\leq C+a_i$ 的最大值即可。因为数组单调，$j$ 也可以单调移动。当然根据题目不同，指针移动的方向是不同的，但是本质上就是固定其中一个端点，最优性地移动另一个端点。

这样我们就能省去其中一维的枚举，起到优化复杂度的目的。

例题

决策单调性对一类 1D/1D DP 的优化

这里 xD/yD DP 意思是状态数有 $n^x$ 种，每个状态的转移有 $n^y$ 种的 DP。而 1D/1D DP 通常长这样
$$
f_i = \min(\max){f_j+w(i,j)}
$$

而决策单调性是指，对于两个决策点 $j$ 与 $k(j<k)$，如果对于状态 $i$，决策 $​k$ 优于 $​j$，那么对于 $​\forall i′(i′>i)$ 都有 $k$ 优于 $j$，即从 $k$ 转移一定更优，$j$ 一定不再会成为最优决策，决策是单调的，和上文提到的双指针优化有点类似。

未经优化的 1D/1D DP 通常复杂度是 $O(n^2)$。这部分将围绕 $w(i,j)$ 不同的性质分情况来讨论不同的优化方法。注意多维 DP 中某一维可能也是 1D/1D 的，那么这一维也是可以单独拿出优化的，因此下面只讨论纯粹的 1D/1D DP。

在这里，笔者叙述的思路是先讨论几个常见的优化方法，之后再引出其共同点以及一些拓展。内容有一定连续性，不建议跳跃阅读。

$w(i,j)$ 只含 $i$ 和 $j$ 的项——单调队列优化

我们不妨将转移写成 $f_i = \min(\max){f_j+a[i]+b[j]}$，以 $\min$ 为例。

因为 $a[i]$ 与 $j$ 无关，实际上转移就是 $f_i = \min{f_j+b[j]}+a[i]$。那么我们只要找到 $\min$ 括号内最小的即可。

若 $1\leq j<i$，请移步前缀和优化。而一般来说 $j$ 都是在一个移动的区间取值的，并且随 $i$ 移动而移动，我们设为 $[l_i,r_i]$，$l_i,r_i$ 单调不减。

那么我们就只需维护一个单调递增的单调队列，单调队列中存放 $f_j+b[j],j\in[l_i,r_i]$，并且对应的下标也单调递增。对于每一个 $i$，我们先将新增区间部分从队尾加入单调队列，因为需要维护单调性，如果尾部的元素大于需要加入的元素直接舍弃，因为它不可能成为最优决策点。接着考虑队首元素是否在可转移区间内，若不满足就一直出队直到找到一个满足条件的队首。那么此时的队首是 $[l_i,r_i]$ 中的最小值，更新 $f_i$。

例题

单调队列优化多重背包

一般的多重背包方程式通常是 $f_{i}$ 表示容积为 $i$ 时的最大价值。转移大概是（其中物品种数 $n$，容积 $V$，第 $i$ 个物品有 $c_i$ 个，体积 $v_i$，价值 $w_i$）

for (int i = 1; i <= n; i++)
    for (int k = 1; k <= c[i]; k++)
        for (int j = V; j >= v[i]; j--)
            f[j] = max(f[j], f[j-v[i]]+w[i]);

显然复杂度是 $O(V\sum c_i)$。一种可行的优化方法是二进制分解，大致思路是将每种物品的个数基于二进制分解为 $O(\log c_i)$ 个不同的物品，再用这些分解后的物品做 01 背包，复杂度 $O(Vn\log c)$。

另一种方案就是利用单调队列来优化。大致思路就是考虑放第 $i$ 种物品时，我们将 $f$ 中模 $v_i$ 同余 $x,x\in[0,v_i)$ 的下标拿出来拼在一起记作 $g$，即 $g_j=f_{(j-1)v_i+x}$ 。那么实际上，原方程 $f_j = \max\limits_{1\leq k\leq c_i}{f_{j-v_i\times k}+w_i\times k}$ 等价于 $g_j = \max\limits_{1\leq k\leq c_i}{g_{j-k}+w_i\times k}=\max\limits_{j-c_i\leq a<j}{g_a+w_i\times (j-a)}$。这个是可以单调队列优化的。综上复杂度变成了 $O(Vn)$。

例题就不给了，随便找个多重背包模板改了交上去就好了。

$w(i,j)$ 只含 $i,j$ 和 $ij$ 的项——斜率优化

将转移写成 $f_i = \min(\max){a[i]\times b[j]+c[i]+d[j]}$，式子中不含 $f_j$ 是因为 $f_j$ 可能参与了 $b[j]$ 和 $d[j]$ 的运算，为了方便表达就直接将 $f_j$ 隐去了，不过这是不影响后续讨论的。同时，这种形式的决策单调性的优化 $a,b$ 需要满足一些条件，这里以 $a$ 单调递减，$b$ 单调递增为例，至于原因以及其他适用条件，在之后的讨论会给出。还是以 $\min$ 为例。

那么现在需要的就是对于每个 $i$，找到最优决策点 $j$。对于每个 $i$，只有跟 $j$ 有关的是变量。于是我们将原式子变形
$$
-d[j]=a[i]\times b[j]+c[i]-f_i
$$

我们用线性规划来解决这个问题。用一次函数 $y=kx+b$ 来描述这个方程。那么 $y=-d[j],x=b[j]$，并且 $k=a[i],b=c[i]-f_i$。我们现在需要 $f_i$ 尽可能小，显然就是要 $b=c[i]-f_i$ 尽可能大，也就是在 $y$ 轴上的截距尽可能大。于是我们对于 $1\sim i-1$ 间所有的 $j$，把 $(b[j],-d[j])$ 刻画在坐标轴上，再用 $y=a[i]x+b$ 去做线性规划，如图。



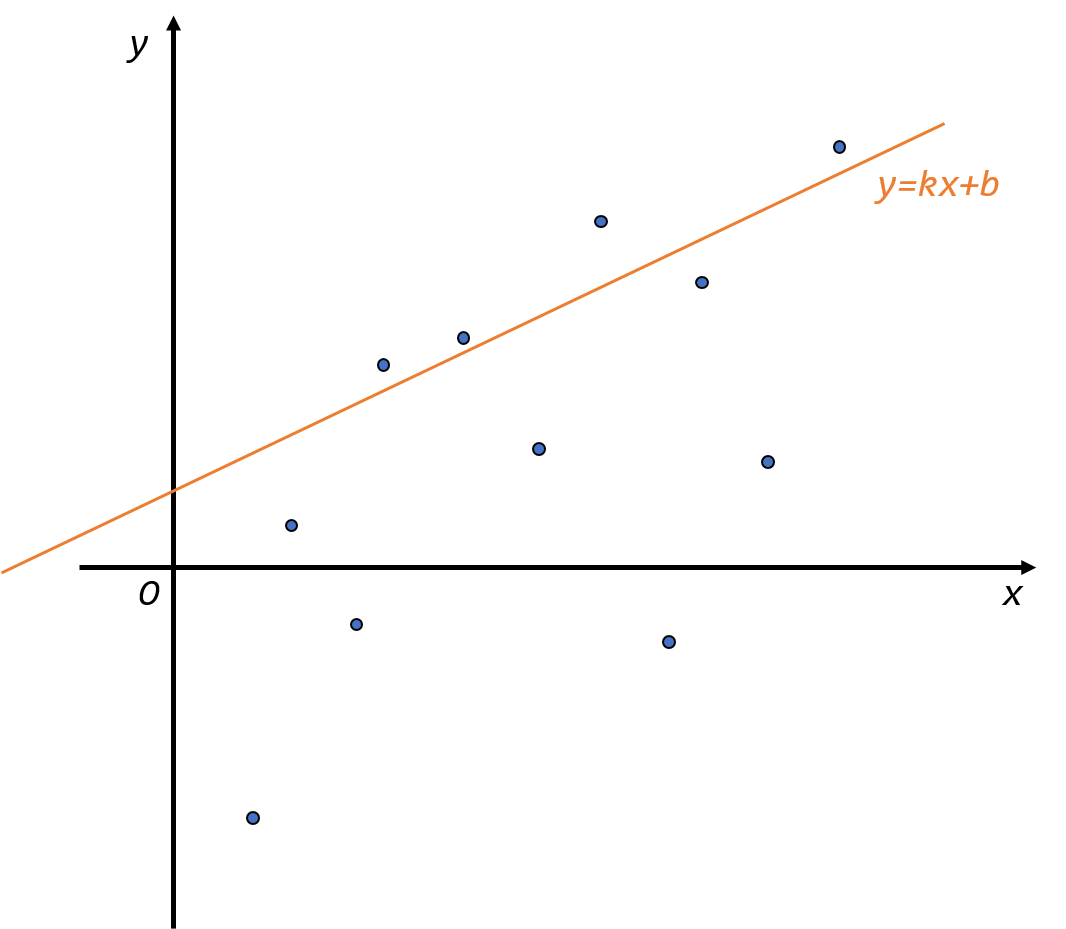
显然需要截距最大时，直线必切于这些点的上凸包，于是我们只需要维护这一个上凸包即可。



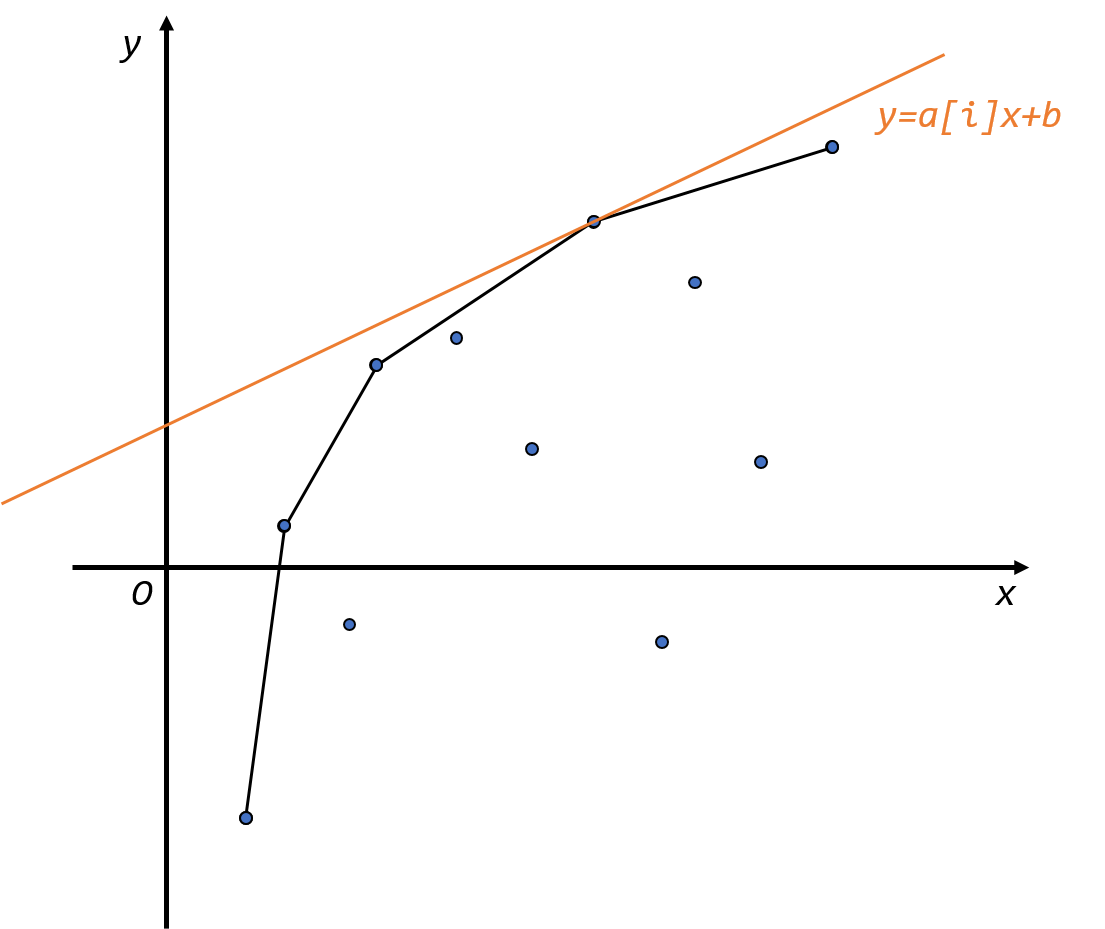
而如何在 $i$ 不断枚举时，在不断有新的点加入的情况下去维护这一个上凸包呢？之前在提出问题的时候说明了，$b[j]$ 是单调递增的，也就是说当我的循环变量 $i$ 往右枚举时，新增的点会出现在所有之前的点的右边。我们开一个单调队列依次存下凸包上的点，单调队列中相邻的两点斜率是单调递减的。显然如果新加入的点会导致出现下图的情况，那么就把队尾的点删掉，因为它不可能再成为最优决策点。删除之后再重复这一过程，直至不出现如下的情况。（黄点为新加入的点，其余为原凸包上的点。）



而即使维护了这个上凸包，若还是用遍历凸包上的点来找最优决策点的话依旧是不可以的。于是这里需要决策单调性优化，之前也保证了 $a[i]$ 是单调递减的，如图。那么显然若 $i$ 的最优决策点为 $j$，那么 $\forall i'\geq i$，$i'$ 的最优决策点 $k$ 一定满足 $k\geq j$。



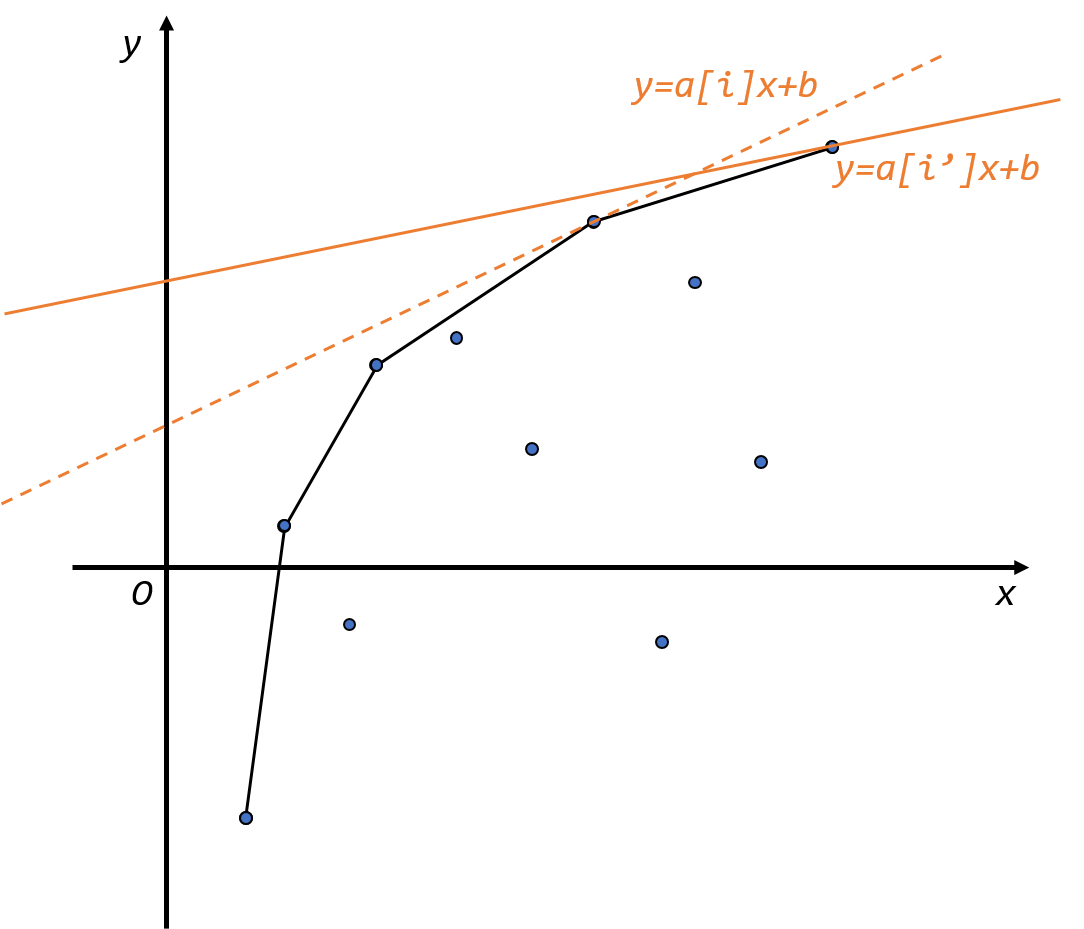
并且对于最优决策点，记它与之前的一个点斜率为 $k_1$，它与之后的一个点斜率为 $k_2$，需要满足 $k_1> a[i]> k_2$。因此每当做决策前，我们先判断队首与次队首的斜率是否 $>a[i]$，若是，队首出队，直至队首与次队首连线的斜率 $<a[i]$。至此，队首元素就是对于 $i$ 时的最优决策点。

综上，由于每个点最多只会进出队列各一次，所以我们就可以 $O(n)$ 解决这一问题了。

回到这一部分的最初的问题，究竟那些性质的 $a,b$ 可以用决策单调性的斜率优化，并且原因又是什么呢？当然你可以通过画图来解释，但是下文将给出一个更加普适的原理。

决策单调性适用的原理——四边形不等式与决策单调性

在解释斜率优化那部分的遗留问题前，我们需要先对决策单调性这一整个部分进行归纳总结。

四边形不等式：对于任意 $a\leq b\leq c\le d$，有 $w(a,d)+w(b,c)\geq w(a,c)+w(b,d)$。

注意，四边形不等式不同于代数上的不等式。它只是一些 $w$ 的二元函数具备的某种特殊性质。

定理：若 $w(i,j)$ 满足四边形不等式，那么 1D/1D DP 是可以用决策单调性优化的。

实际上某些情况下不等号是 $\leq$ 而不是 $\geq$。并且这两者适用的 DP 以及单调性是有些许差别的，具体地

  • 当四边形不等式不等号取 $\geq$ 时，若转移方程是取 $\min$ 值，那么最优决策点与 $i$ 的移动方向相同，并且单调；
  • 当四边形不等式不等号取 $\geq$ 时，若转移方程是取 $\max$ 值，那么最优决策点与 $i$ 的移动方向相反，并且单调；
  • 当四边形不等式不等号取 $\leq$ 时，若转移方程是取 $\min$ 值，那么最优决策点与 $i$ 的移动方向相反，并且单调；
  • 当四边形不等式不等号取 $\leq$ 时，若转移方程是取 $\max$ 值，那么最优决策点与 $i$ 的移动方向相同，并且单调。

注意，这四种不同的单调性差别值得注意，由于下文为了行文方便，均以第一种情况为例，千万不要以偏概全，对于题目要具体问题具体分析。

证明：以上述优化的第一种情形为例，即 $f_i = \min{f_j+w(i,j)}$，并且 $w$ 要满足 $w(a,d)+w(b,c)\geq w(a,c)+w(b,d)$。
设 $p_i$​ 表示 $i$ 的最优决策点是 $p_i$。那么有
$$f_{p_i}+w(p_i,i)\leq f_j+w(j,i)\tag{1}$$
同时，我们需要证明的式子是
$$f_{p_{i+1}}+w(p_{i+1},i+1)\leq f_j+w(j,i+1)\tag{2}$$
将 $(2)$ 式中 $j$ 变为 $p_i$
$$f_{p_{i+1}}+w(p_{i+1},i+1)\leq f_{p_i}+w(p_i,i+1)\tag{3}$$
下面需要分情况讨论
1. $p_{i+1}=i$，那么显然 $p_{i+1}=i\geq p_i$ 的，满足决策单调性；
2. $p_{i+1}\neq i$，将 $(1)$ 式中 $j$ 变为 $p_{i+1}$，那么
$$f_{p_i}+w(p_i,i)\leq f_{p_{i+1}}+w(p_{i+1},i)\tag{4}$$
$(3)+(4)$ 得
$$w(p_{i+1},i+1)+w(p_i,i)\leq w(p_i,i+1)+w(p_{i+1},i)$$
若 $p_i>p_{i+1}$，代入上式，可以发现不等号与原四边形不等式不等号方向相反，显然矛盾。因此 $p_i\leq p_{i+1}\leq i\leq i+1$。
综上满足 $p_i\leq p_{i+1}$，即满足决策单调性。
其余三种情况可以用同种方式证明，这里从简略去。读者可以自行证明。

既然如此，前文的单调队列优化以及斜率优化均利用到了决策单调性。那它们的 $w$ 函数都是满足四边形不等式的，下面给出证明。为了方便下面默认四边形不等式是 $\geq$ 的，并且 DP 值是取 $\min$ 的。

对于单调队列优化来说，$w(i,j)=a[i]+b[j]$。那么对于 $i\leq j\leq p\leq q$
$$\begin{aligned}
w(i,q)+w(j,p)&=a[i]+b[q]+a[j]+b[p]\
w(i,p)+w(j,q)&=a[i]+b[p]+a[j]+b[q]
\end{aligned}$$
由于 $a[i]+b[q]+a[j]+b[p]=a[i]+b[p]+a[j]+b[q]$。显然 $w(i,q)+w(j,p)\geq w(i,p)+w(j,q)$，满足四边形不等式。

对于斜率优化来说，$w(i,j)=a[i]\times b[j]+c[i]+d[j]$。那么对于 $i\leq j\leq p\leq q$
$$\begin{aligned}
w(i,q)+w(j,p)&=a[i]\times b[q]+c[i]+d[q]+a[j]\times b[p]+c[j]+d[p]\
w(i,p)+w(j,q)&=a[i]\times b[p]+c[i]+d[p]+a[j]\times b[q]+c[j]+d[q]
\end{aligned}$$
要使其满足四边形不等式，即 $a[i]\times b[q]+c[i]+d[q]+a[j]\times b[p]+c[j]+d[p]\geq a[i]\times b[p]+c[i]+d[p]+a[j]\times b[q]+c[j]+d[q]$。等价于
$$a[i]\times b[q]+a[j]\times b[p]\geq a[i]\times b[p]+a[j]\times b[q]$$
那么至此，$a,b$ 适用于决策单调性的斜率优化需满足的条件也迎刃而解了，即满足上式即可。

通过对 $w$ 的符号的讨论，并且由排序不等式，对于上面的式子，更进一步的推论是，决策单调性的斜率优化需要满足的条件就是

  • 当 $w$ 符号取 $\geq$，DP 取 $\min(\max)$ 值时，$a$ 与 $b$ 的单调性相反即可，只不过要根据决策点向左/向右移动来选择单调栈/单调队列维护。
  • 当 $w$ 符号取 $\leq$，DP 取 $\min(\max)$ 值时，$a$ 与 $b$ 的单调性相同即可，同上。

其实本质上就是使得 $w$ 有四边形不等式的性质。

因为内容编排的原因，至此给出决策单调性斜率优化的例题。

例题

$w(i,j)$ 满足四边形不等式的更一般的情形——分治/二分数据结构

由上面的分析，我们可以得出对于 1D/1D 类 DP 的决策单调性优化是需要 $w$ 满足四边形不等式的。不过之前举例的单调队列优化和斜率优化对于 $w$ 的要求比较特殊，那么能不能有一种普适的做法使得让 $w$ 只要满足四边形不等式就可以优化呢。

举例来说当 $w(i,j)=\sqrt{j-i}$，这个式子是满足 $\forall a\leq b\leq c\leq d,w(a,d)+w(b,c)\leq w(a,c)+w(b,d)$。不过式子中的 $i,j$ 是不能像之前的情况一样独立出来的。于是我们考虑用别的方法来解决。

同样，为了行文方便，均以决策点向右移动为例。

分治

当 DP 方程满足
$$
f_i = \min(\max){g_j+w(i,j)}
$$

其中 $g$ 与 $f$ 无关。这时，可以用分治的方法来解决。

例如，考虑我们需要得到 $[L,R]$ 这个区间的 DP 值，并且备选的决策区间是 $[l,r]$。若对于 $MID\left(MID=\frac{L+R}{2}\right)$ 这个位置的 DP 值取最优时的决策点是 $loc$，那么由决策单调性，$[L,MID-1]$ 的备选区间就是 $[l,loc]$，而 $[MID+1,R]$ 的备选区间是 $[loc,r]$。这样把问题分成两个子问题分治递归下去。

而如何找到 $loc$，方法是直接暴力扫 $[l,r]$ 中所有点作为决策点去转移到 $MID$ 上，找到其中的最优值。以 CDQ 分治的思想，整个算法时间复杂度是 $O(n\log n)$ 的。

由于转移时的 $f$ 取值是不会受其他位置的 $f$ 值的影响的，这样就保证了每个 $f$ 的计算不需要先决条件，这样就能保证分治的正确性。

例题

二分+数据结构

而当 DP 方程满足
$$
f_i = \min(\max){f_j+w(i,j)}
$$

也就是说 $f$ 的取值是受前面别的 $f$ 的取值的影响的，这样分治的方法就不奏效了，这时有另外一个方法来解决——二分数据结构，通常使用二分+单调队列/单调栈来实现。

在方法讲解之前，我们需要给出一个引理。

引理：对于 $w$ 满足四边形不等式的 DP 中 $\forall i<j$，如果在 $i$ 处决策点 $n$ 比 $m$ 优秀（$m<n$），那么在 $j$ 处 $n$ 同样比 $m$ 优秀。

证明：还是以 $\geq$ 的四边形不等式以及取 $\min$ 的 DP 方程为例。
由含义 $m<n<i<j$，那么满足四边不等式
$$w(m,j)+w(n,i)\geq w(m,i)+w(n,j)\tag{1}$$
又由于 $n$ 在 $i$ 点作为决策比 $m$ 优，即
$$f_m+w(m,i)\geq f_n+w(n,i)\tag{2}$$
$(1)+(2)$ 得
$$f_m+w(m,j)\geq f_n+w(n,j)$$
得证。

在这之前我们所有的 DP 方法都是对于每个位置，考虑最优决策点。不过这个方法是对于每个位置，考虑其能成为哪些 DP 值的最优决策点。

由于满足决策单调性，显然最终每个位置的最优决策点是单调递增的，例如（数字表示每个位置的最优决策点，下标从 0 开始）

00112222234444666

在整个算法最开始时，由于考虑的决策点只有最初的 0，因此此时每个位置的最优决策都是 0，即

00000000000000000

对于 1 这个点由于只能从 0 这个点转移，因此 0 就是 1 的最优决策点，计算出 $f_1$。之后考虑 1 作为决策点对于哪些点来说能比 0 的决策更优。由之前引理，1 一定会是连续的一段后缀（也可能不存在），例如

00111111111111111

而如何找到最左端这个 1，我们可以二分来解决。对于二分的位置，如果它用 1 更新更优，那么把右端点左移，查找是否有更靠左的位置，否则左端点右移。找到最优点之后，那么右边这一段就全是 1 了。我们可以开一个三元组 $(i,l_i,r_i)$ 表示 $i$ 这个决策点控制范围为 $[l_i,r_i]$ 用队列维护，这样就不用额外地赋值了。

以此类推，2 这个点从 1 转移，更新后续的决策点。循环把 $1\sim n$ 做完即可。这其中，一共有三种不同的更新情形

  1. 队尾区间未被完全覆盖，这个时候显然二分出最左端的更新位置之后，把当前队尾的右端点更新，再把新的这个三元组加进队尾。
  2. 新的元素不比任何一个更优，我们只需要在二分前做一次特判，看新的元素更新 $n$ 这个位置是否比之前的更优，若否，那么显然这个元素不可能成为后续的最优决策，舍掉。
  3. 队尾区间能被完全覆盖，也就是说，例如原来的最优决策点是
    00112222234444666

    新加入的 7 这个点能完整地覆盖 6，如
    00112222234477777

    那么这时，我们只需在二分前把这种能被完全覆盖的区间去掉就可以了，操作方法是比较队尾元素作为决策点以及新的元素作为决策点转移到队尾元素控制的左端点哪一个更优，若新的元素能更优，把队尾弹出。重复操作后就可以按照 1. 的情形二分了。

几个要注意的小细节：

  1. 二分的区间的左端点是经过第三种情形处理后的队尾元素的左端点，二分的右端点是 $n$。
  2. 情形 3 是可以边二分边弹出队尾的。不过若这样做，一定要注意计算 DP 值的时候千万不要用后面的元素视作前面元素的决策。几个例子
    00112222234444666

    当你计算 4 这个区间的 DP 值时，千万不要拿 6 作为最优决策点来算，因为这样就不满足决策单调性了。所以还是建议先弹出不合法的队尾再进行二分。
  3. 对于每个位置 $i$，它的最优决策点就是队首元素，不过如果队首元素控制范围的右端点在 $i$ 前面，记得把这个队首弹出再取新的队首作为最优决策点。

同样，若决策点单调向左移动，可以用单调栈维护这个过程。

其实，适用于分治的 DP 式子也可以用这个方法做，不过这个方法同样也有一些缺陷，也就是单个 $w$ 计算复杂度较高时，二分的复杂度会退化，也就起不到优化的目的了。

但是分治法中有一个暴力扫的过程，如果 $w$ 可以通过上一个计算出的 $w'$ 简易地推导出，那么分治法就可以解决这一类问题（当然前提还是 $g$ 和 $f$ 互不影响）。例如[Codeforces 868F]Yet Another Minimization Problem这题就只能分治法做。

例题

小总结：

  • $f$ 与 $g$ 无关，或者与此同时 $w$ 不能简易计算出，选择分治法；
  • $w$ 能简易计算出，选择二分+数据结构的方法。

四边形不等式的一点补充

这里对四边形不等式做一些补充，以 $\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)+w(b,c)\geq w(a,c)+w(b,d)$ 这样的四边形不等式为例。

我们取其中的一种特殊情况：取 $i\leq i+1\leq j\leq j+1$，那么 $w(i,j+1)+w(i+1,j)\geq w(i,j)+w(i+1,j+1) (*)$。

同时若 $w$ 满足 $()$，那么 $w$ 也是满足四边形不等式的。即四边形不等式与 $()$ 式是等价条件。具体证明这里从略，感兴趣的读者可以自行证明。

另外，如果我们把 $(*)$ 式移项，得到 $w(i+1,j)-w(i,j)\geq w(i+1,j+1)-w(i,j+1)$。也就是说，随着决策点的右移 $j+1$，此时 $w$ 的增长速率是小于 $j$ 处的速率的。并且如果此时转移方程取 $\min$，显然如果某时 $j+1$ 比 $j$ 优秀，那么之后不可能会有 $j$ 比 $j+1$ 优秀。这样对应了之前总结的单调性规律，可以视为另一种证明。

四边形不等式对 2D/1D DP 的单调性优化

上文说到，如果对于 1D/1D DP，如果转移的代价函数 $w$ 满足四边形不等式，如 $\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)+w(b,c)\geq w(a,c)+w(b,d)$，那么 $f$ 的决策点是满足单调性的。除此之外，四边形不等式的一些性质在优化区间 DP 也有一定的作用。

问题引出：假设有区间 DP 的转移方程是 $f_{l,r}=\min(\max){f_{l,k}+f_{k+1,r}+w(l,r)}$，如果 $w$ 满足四边形不等式以及区间单调性，那么这个式子是可以利用某些单调性优化到 $O(n^2)$ 的。

  • 四边形不等式，还是以 $\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)+w(b,c)\geq w(a,c)+w(b,d)$ 为例。
  • 区间单调性，即 $\forall a,b,c,d, a\leq b\leq c\leq d, w(a,d)\geq w(b,c)$，即小区间的函数值不超过包含其的大区间。并且式中的不等号应时刻与四边形不等式的不等号方向一致。

对于不等号的方向和取 $\min$ 还是取 $\max$ 之间的关系，这里要说明的是当上述不等号取 $\geq$ 时，对应的 DP 方程是要取 $\min$ 的，并且单调性与枚举顺序相同。其余的可以参考上文决策单调性优化得出结论。下面还是以这一种为例。

先不加证明地引出两个引理。（不证明是考虑到引理证出来意义不大，并且没有必要。如果你感兴趣可以参考《动态规划加速原理之四边形不等式(赵爽)》这篇文章）

引理一 对于 DP 方程，$f_{l,r}=\min{f_{l,k}+f_{k+1,r}+w(l,r)}$，若 $w$ 满足四边形不等式和区间单调性，那么 DP 函数 $f$ 同样满足四边形不等式。

引理二 设 $s_{l,r}$ 是 $f_{l,r}$ 的最优决策点。如果 $f$ 满足四边形不等式，那么会有 $s_{i,j}\leq s_{i,j+1}\leq s_{i+1,j+1}$。

四边形不等式定理 若利用引理二的单调性，即 $s_{i,j-1}\leq s_{i,j}\leq s_{i+1,j}$，来优化该区间 DP，其复杂度是可以降低至 $O(n^2)$ 的。

证明：从区间 DP 的本质入手，我们考虑当区间长度为 $\delta$ 时枚举的量。对于每个左端点：
$l=1$，$(l,l+\delta-1)$ 枚举长度是 $s_{l+1,l+\delta-1}-s_{l,l+\delta-2}=s_{2,\delta}-s_{1,\delta-1}$；
$l=2$，枚举长度是 $s_{3,1+\delta}-s_{2,\delta}$；
$l=3$，枚举长度是 $s_{4,2+\delta}-s_{3,1+\delta}$；
$\vdots$
$l=n+1-\delta$，枚举长度是 $s_{n+2-\delta,n}-s_{n+1-\delta,n-1}$。
把上式相加，总长度是 $s_{n+2-\delta,n}-s_{1,\delta-1}\leq n$。又由于总共有 $n$ 个不同的 $\delta$，因此总复杂度为 $O(n^2)$。

例题

事实上，更多的方程并不是长 $f_{l,r}=\min(\max){f_{l,k}+f_{k+1,r}+w(l,r)}$ 这个样子，更多的会是 $f_{i,j}=\min(\max){f_{k,j-1}+w(k+1,i)}$。大致意思是前 $i$ 元素分为 $j$ 个区间得到的最小/大价值。这里值得补充的是如果 $w$ 满足四边形不等式，可以证明 $f$ 同样满足四边形不等式，同样可以优化。

容易发现，这个方程和前文所述 1D/1D 类 DP 决策单调性优化是一样的，因此这些 DP 会有多种优化方式。不过不同的方式优化还是有些许复杂度上的差异，请读者自行思考。

例题

不满足决策单调性的斜率优化

在上文，我们提到过基于决策单调性利用斜率对 DP 进行优化的方法。其大致思想是，通过把 DP 转移方程进行变形，再把每一个转移点抽象成二维平面上的点。用线性规划去求对应 DP 值的最值。这样就可以贪心的去取上（或下）凸包上的点得出答案。由于这一过程遵循以下两个单调性：

  1. 随着 $i$ 往后枚举，平面上新加入的点均出现在已有的点集的右（或左）侧，这样新加入的点一定会在凸包上。因此可以比较加入的点和凸包边缘的点的关系，维护凸包。整个过程复杂度可以做到 $O(n)$；
  2. 随着 $i$ 往后枚举，$i$ 这一点对应的线性规划的直线的斜率是单调的。同时单调数据结构维护的凸包上的点两两相邻的斜率也是单调的，因此如果队首的点不再是 $i$ 点的最优决策点的话，那么可以删掉队首，因为队首不再可能是之后的最优决策点。同样，这个过程复杂度也为 $O(n)$。

如果不满足上述两点，那么就不能用决策单调性 $O(n)$ 进行优化了。为了解决这一问题，我们分别考虑下述情形。

直线斜率不单调——二分凸包

由于加入的点的横坐标依旧是满足单调性的，因此，维护凸包这一操作可以沿用上述操作。唯一需要考虑的就是如何在凸包上找到最优决策点。

既然询问的直线不再满足斜率单调，因此队首的点不能轻易删除，也更不能取队首作为最优决策点了。但是由于数据结构中维护的凸包上相邻的两点之间斜率是单调的，那么我们可以考虑在凸包上二分，找到这样一个位置 $j$，使得直线可以正好相切于 $j$ 点，那么这一点就是最优决策点。二分时注意边界的取舍。

例题

加入点横坐标不单调——平衡树维护凸包/CDQ 分治

加入点横坐标位于之前的点之间时，可以考虑用平衡树来维护这一凸包。这样就可以支持在 $O(\log n)$ 的时间里维护凸包和查询。不过相比而言，考虑到代码复杂度，CDQ 分治实现更为常用。因此不再赘述平衡树维护凸包的实现细节。

如果采用分治实现的话。考虑当前分治区间 $[l,r]$。需要做的就是计算 $[l, mid]$ 这一部分转移到 $[mid+1, r]$ 的贡献。大致分以下几步

  1. 先递归处理 $[l, mid]$ 这一区间；
  2. 对 $[l, mid]$ 区间内所有点按横坐标排序，用决策单调性的方法维护这一区间内的上（或下）凸包；
  3. 之后把 $[mid+1, r]$ 区间内所有的点按询问的直线斜率排序，同样用决策单调性的方法去询问；
  4. 递归处理 $[mid+1, r]$ 区间。

这样就可以在 $O(n\log^2 n)$ 的复杂度内解决这一问题。

优化：其实归并排序也是分治过程，如果把快排换成归并排序的话，就可以将复杂度优化成 $O(n\log n)$。

值得注意的是，处理点横坐标不单调这一情况时也可以同时处理询问直线斜率不单调的情况。

例题

带权二分优化（DP 凸优化）

通常我们会遇到这样的问题：给定 $n$ 个元素，每个元素有不同的属性，规定某一属性必须选 $k$ 个，最大/最小化价值；或者给定长度为 $n$ 的序列，让你恰好划分为 $k$ 段，最大/最小化价值。令 $g(x)$ 表示这一属性必取 $x$ 个（或序列恰好划分为 $x$ 段）时，所有方案中的最大/最小价值。如果 $g(x)$ 满足是上凸/下凸，那么可以采用凸优化的方法优化这一问题（不限于 DP）。我们以下一题为例子。

例题

  • [BZOJ 2654]tree(陈立杰)

    给你一个 $n$ 个点 $m$ 条边的无向带权连通图，每条边是黑色或白色。让你求一棵最小权的恰好有 $need$ 条白色边的生成树。
    $1\leq n\leq 50000, 1\leq m\leq 100000$

我们设 $g(x)$ 表示，在所有恰好有 $x$ 条白边的生成树中，边权和最小的生成树的边权和。显然 $g$ 函数是不能直接求出来的，不过我们可以大致感受到 $g$ 函数是一个下凸函数，如下图



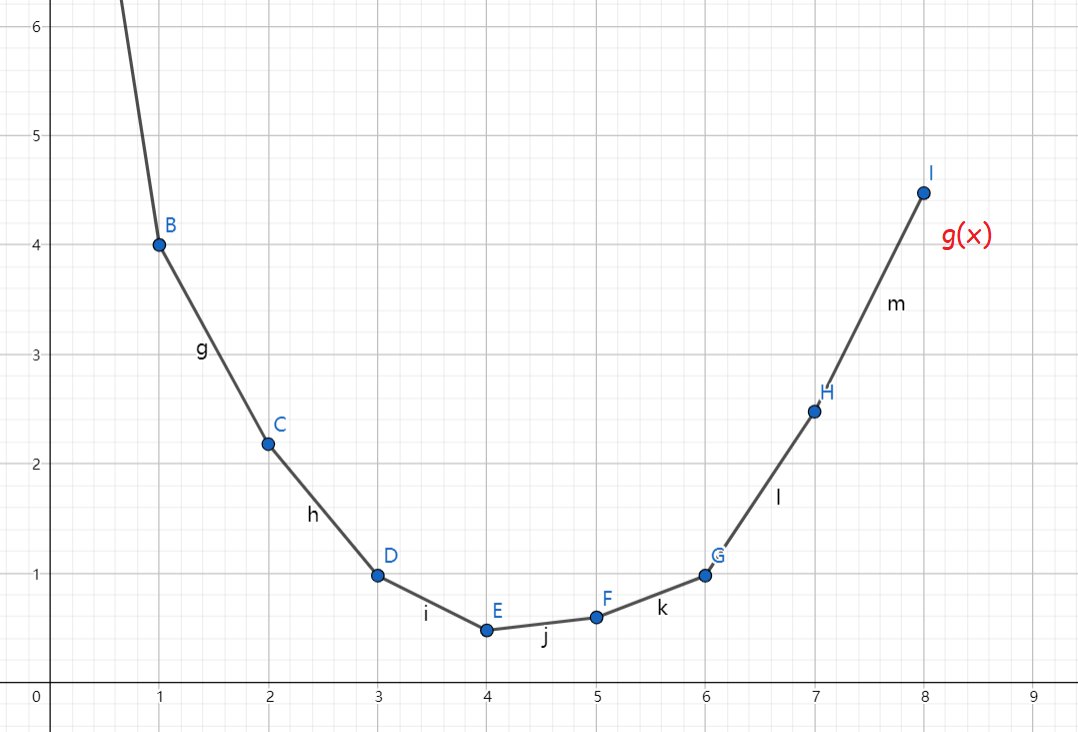
图中的最低点 $(x=4)$ 的纵坐标也就是这幅图的最小生成树权值和，即这幅图的最小生成树中恰有 4 条白边。但其实对于 $y=g(x)$ 上所有的点的纵坐标，只有最低点是可以利用最小生成树算法算出结果的，其余无从计算。

那么当我们需要求解别处的 $g$ 的取值时（如求 $g(3)$），我们有这样一个思路——让这一点成为整个图像的最低点。

由于这一个函数下凸。那么假如用一直线 $y=kx+b$ 去截这一图像，联立方程 $\left{\begin{aligned}y&=g(x)\ y&=kx+b\end{aligned}\right.$ 也就是 $b=g(x)-kx$。令 $f(x)=b$，可以观察出 $f(x)$ 取最小的时候，也就是直线与 $y=g(x)$ 相切时。如果这一切点恰好为 $x=3$ 处的点，那么 $f$ 的最小值就是 $f(3)=g(3)-3k$。因此如果我能求出恰当的斜率 $k$ 以及对应的最小值 $f(3)$，那么也就求出了 $g(3)$。



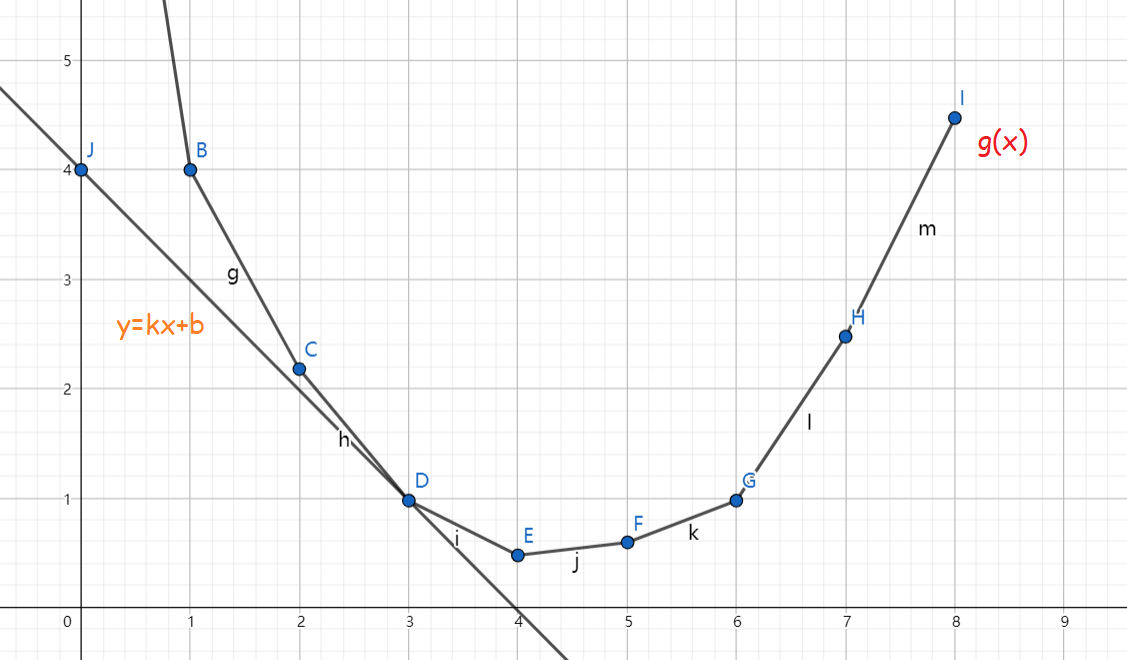
假设 $k$ 确定，那么问题就只剩求出 $f$ 的最小值。由于 $f(x)=g(x)-kx$，实际意义就是恰有 $x$ 条白边的最小生成树权值减去白边数 $\times k$。那么我们可以将原图内所有的白边权值都恰好减去 $k$，再求修改后图的最小生成树。那么求出来的权值就是最终的 $f(3)$。

那么如何求 $k$ 呢？由于 $y=g(x)$ 下凸，也就是斜率是单调不减的，因此可以考虑二分 $k$ 值。如果当前 $k$ 值求出的最小生成树包含 $>3$ 条白边，那么斜率应减小，缩减二分上界。反之亦然。这样我们就可以在 $O(m\log m\log w)$ 的时间复杂度内解决这一问题，其中，$w$ 为二分值域。

同样对于其他的类似的问题，我们也可以通过类似地方法在 $O(T(n)\log w)$ 的之间内求出想要问题的解，$T(n)$ 为求解无 $k$-约束问题的时间复杂度，$w$ 为二分值域。

这一方法有两个遗留的小问题，这里说出并且做出解答：

  • 二分值域的选择。这一个可以根据具体问题，或者通过对凸包最大/最小斜率的估计得到；
  • 可能存在整数二分时不能找出恰当的 $k$，让其相切于目标点。也就是比如 $k=i$ 时，相切的点 < 目标点。$k=i+1$ 时，相切的点 > 目标点。在通常情况下，出现这种问题是因为目标点及其左右的点共线，导致在当前 $k$ 取值的情况下多个点都是函数最低点。出现这种问题的处理方式是考虑利用这几个点共线的性质，直接通过前后的点计算出该点权值。之前的例题便运用了这一方法，可以参考这一做法。

容易发现带权二分其实就是将一个 $k$-约束最值问题，通过凸函数的性质，转化为无约束的最值问题，从而将复杂度中的因子 $m$ 变成对数，降低复杂度。如果最初问题是一类有约束的 DP 问题并且满足凸性，那么就可以用这一方法优化 DP 了。

有时候最初的问题是 2D/1D DP 问题（如：$f_{i, j}$ 表示前 $i$ 个元素中选出符合条件的 $j$ 个时最小/大价值），并且这一问题满足凸函数性质，那么就可以用带权二分优化这一 DP 变成 1D/1D 类 DP，这时候可能还可以用到上文所提到的一些优化方法将这一 DP 再进一步地优化。

例题

数据结构优化

数据结构优化 DP 实际上没有太多总结性的东西。主要是需要根据 DP 转移方程，适当地选取数据结构优化转移时的枚举、修改过程。结合数据结构本身对数据维护的的特点对当前的 DP 进行优化。常见的有树状数组、线段树、平衡树、线段树合并、bitset 等等。

例题

参考文献

posted @ 2020-01-30 14:15  NaVi_Awson  阅读(2667)  评论(14)  编辑  收藏  举报