『学习笔记』线段树
线段树和树状数组都是用来优化序列操作的数据结构。
线段树理解容易,常数大,解决问题范围广;树状数组理解比较困难,常数非常小,能解决的问题就没有线段树多了,可以说树状数组能解决的问题是线段树能解决的问题的子集。
基本概念
线段树是一个二叉树,每个节点表示一个区间。
对于任意节点,要么是叶子节点,要么两个儿子都存在。
它可以快速在序列上修改及查询元素,可以是区间修改或查询。每次修改或查询的时间复杂度为 \(\mathcal{O}(\log n)\)。在使用之前,还需花费 \(\mathcal{O}(n)\) 的时间建树。
那么每个节点存什么?
- 如果是叶子节点,就存需要执行操作的序列的对应项。具体是哪项下面再说。
- 否则,就存这个节点的左右儿子之和或最小值、最大值、乘积等等。以求和为例,计算公式为 \(t_x=t_{\operatorname{left\_son}(x)}+t_{\operatorname{right\_son}(x)}\)。这个节点的值就是这个节点表示的区间之和。
为方便表示,本文中的 ls(x) 均代表 \(x\) 节点的左儿子节点,rs(x) 同理。
每个节点的儿子表示的区间都是当前节点区间的一半,左儿子表示的是 \(\left[l,\left\lfloor \dfrac{l+r}{2} \right\rfloor\right]\),右儿子表示的是 \(\left[\left\lfloor \dfrac{l+r}{2} \right\rfloor+1,r\right]\)。
例如,要使用一个长度为 \(8\) 的序列 \(a=[1,1,4,5,1,4,1,9]\) 构造一棵线段树,那么这棵线段树长这样:
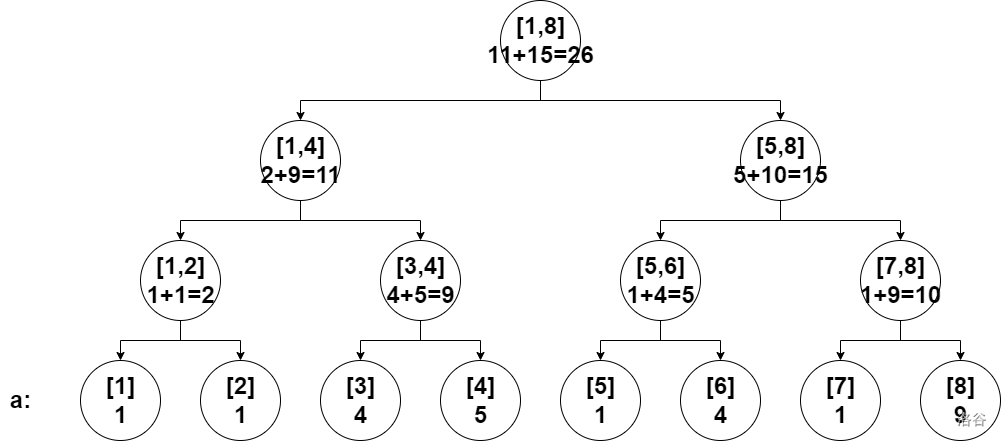
各个非叶子节点的值都是根据 \(t_x=t_{\operatorname{ls}(x)}+t_{\operatorname{rs}(x)}\) 来计算的。
图中每个节点上面写的是这个节点包含的区间,下面写的是各个节点的值。
非叶子节点的值的计算过程也写了上去。
可以发现,表示第 \(i\) 个数的叶子节点的值就是 \(a_i\)。
线段树差不多就长这样子,下面来看详细的操作过程。
实现
如何存储
我们可以使用二叉堆的方式存储:根节点的位置为 \(1\),每个节点的左右儿子的位置分别为 \(i \times 2\) 和 \(i \times 2+1\)。
也就是说,你遍历存储这棵树的数组,和层次遍历这棵树一样。
若有空缺的位置,需要留着。
因为存储的节点除了最后一层还有许多个节点,所以数组长度要比 \(n\) 大。
有人计算过,存树的数组需要开到 \(4n\) 才行。
树的节点结构体定义如下:
struct node{
int l,r; // 表示区间
T v; // 当前值
}t[N<<2]; // 线段树存储数组
建树
呵呵,正文终于开始了。
上面提到过,建树要用 \(\mathcal{O}(n)\) 的时间复杂度进行。因为有 \(n\) 个元素。
使用深度优先搜索的方式来遍历整棵树。遍历的中间,为各个节点的 \(l\) 和 \(r\) 赋值。
遍历到叶子节点(当前的 \(l=r\))时,这个叶子节点的值就应该是 \(a_l\)。
两个儿子都遍历过后,需要通过已经处理好的儿子实时计算当前节点的值。
流程大概是这样的:
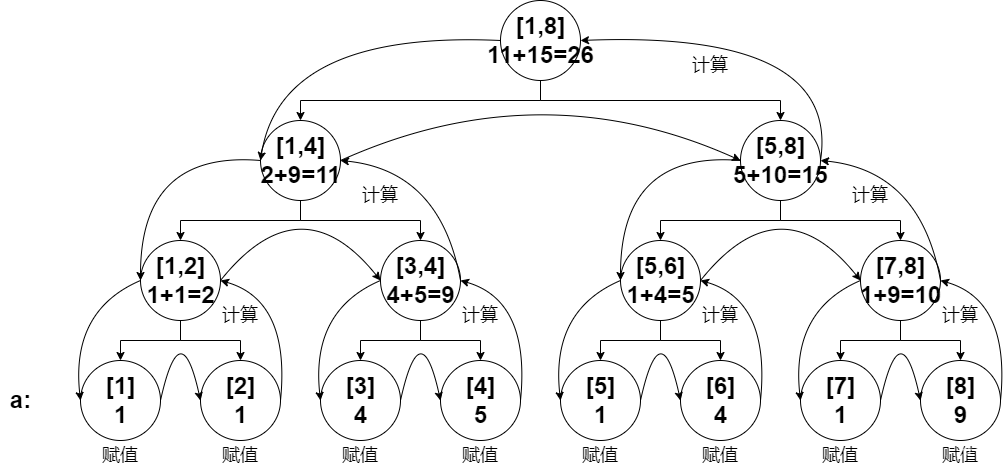
为方便起见,我们定义一个函数 pushup 用来计算当前节点的值。
inline void pushup(int rt){
t[rt].v=t[ls(rt)].v+t[rs(rt)].v; // 计算当前节点的值
}
通过修改 pushup 函数,可以直接修改线段树维护内容。
例如,将其修改为维护最大值的线段树:
inline void pushup(int rt){
t[rt].v=max(t[ls(rt)].v,t[rs(rt)].v);
}
看代码吧!还是代码形象一点:
void build(int rt,int l,int r){ // rt 表示当前节点,l 和 r 表示当前节点表示的区间
t[rt].l=l,t[rt].r=r; // 首先的一步就是指定当前节点表示的区间范围
if(l==r){ // 叶子节点情况
t[rt].v=a[l]; // 为叶子节点赋值
return; // 碰到叶子节点了就要回溯了
}
int mid=l+r>>1; // 计算区间分界点
build(ls(rt),l,mid); // 递归遍历左儿子
build(rs(rt),mid+1,r); // 递归遍历右儿子
pushup(rt); // 计算当前节点值
}
应该很好理解,就是常数...
单点修改
废话了那么多,终于开始说操作了...
单点修改,就是要修改数列中的一个数。
那么在线段树中,就是修改其中一个叶子节点,我们需要修改某个叶子节点后维护整棵线段树,使其还是保持原来的特性(非叶子节点等于两个儿子的和等特性)。
例如,要修改下标为 \(6\) 的数为 \(8\)。
从根节点一直向下找,查找要修改的叶子节点。
若当前搜索的的节点不是叶子节点,那么就需要判断需要修改的叶子节点在左儿子里还是右儿子里:
- 令 \(mid \gets \left\lfloor \dfrac{l+r}{2} \right\rfloor\)。
- 若下标 \(idx \leq mid\),则说明在左儿子里,向左儿子中搜索。
- 否则,就去右儿子。
代码如下:
int mid=t[rt].l+t[rt].r>>1; // 找中间点
if(idx<=mid) update(ls(rt),idx,v); // 进左儿子
else update(rs(rt),idx,v); // 右儿子
最终一定会找到一个叶子节点,它就是我们需要修改的。
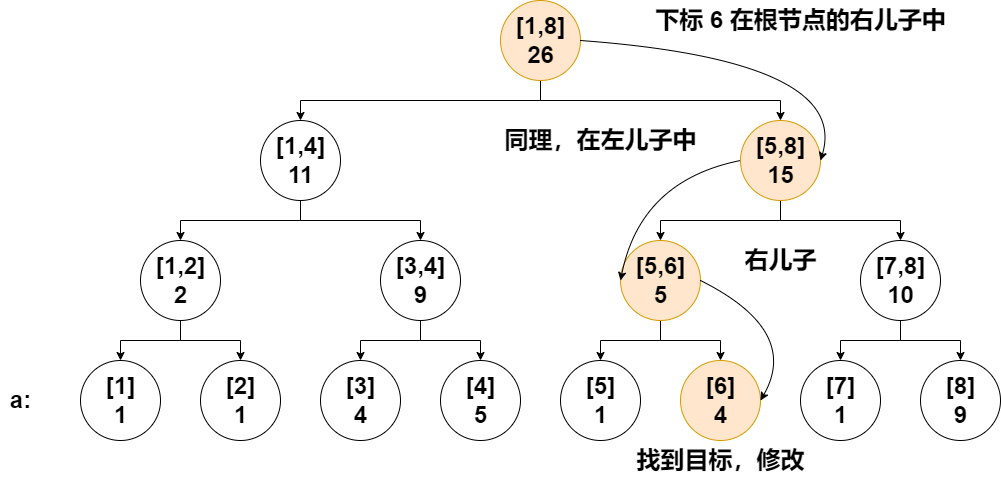
单纯修改叶子节点会破坏整棵线段树的平衡,所以回溯时需要更新查找需要更改的叶子节点时经过的节点。
在函数末尾加上一句 pushup(rt) 即可。
完整代码:
// rt 是当前节点,idx 是需要修改的数的下标,v 是要替换的数(或累加的数)
void update(int rt,int idx,T v){
if(t[rt].l==t[rt].r){ // 找到叶子节点的情况
t[rt].v=v; // 修改
return; // 回溯
}
int mid=t[rt].l+t[rt].r>>1;
if(idx<=mid) update(ls(rt),idx,v);
else update(rs(rt),idx,v);
pushup(rt); // 找到叶子节点后需要将路径上的所有节点都更新一下,从下向上更新
}
很容易看出来,时间复杂度是 \(\mathcal{O}(\log n)\)。别看比暴力还差,区间查询可是 \(\mathcal{O}(\log n)\) 的。
单点查询
没什么好说的,就是从一棵树上找到叶子节点,return 就是了。
这个应该看代码就够了。
T query(int rt,int idx){ // 参数就不多说了
if(t[rt].l==t[rt].r){ // 找到目标
return t[rt].v;
}
int mid=t[rt].l+t[rt].r>>1;
if(idx<=mid) return query(ls(rt),idx); // 在左儿子中
else return query(rs(rt),idx); // 右儿子
// 这里不需要 pushup,因为没有任何修改
}
区间查询
我们之所以维护整棵线段树就是为了使这个操作的时间复杂度变为 \(\mathcal{O}(\log n)\)。
暴力查询时是一个一个累加,但有了线段树就不一样了。
线段树的节点除了叶子节点都存储的是一个区间的和,若某个节点表示的区间在查询区间之内,那么就可以 \(\mathcal{O}(1)\) 地累加出这个节点表示的区间的和。
那如果当前节点表示的区间和查询区间有交集,但并不是查询区间的子集,咋办?
直接看看左右儿子表示的区间是否与查询区间有交集,如果有,则进入相应的儿子查询(两个儿子随便去,但没有都不去的情况,那样当前节点表示的区间要么是查询区间的子集,要么就与查询区间没关系)。
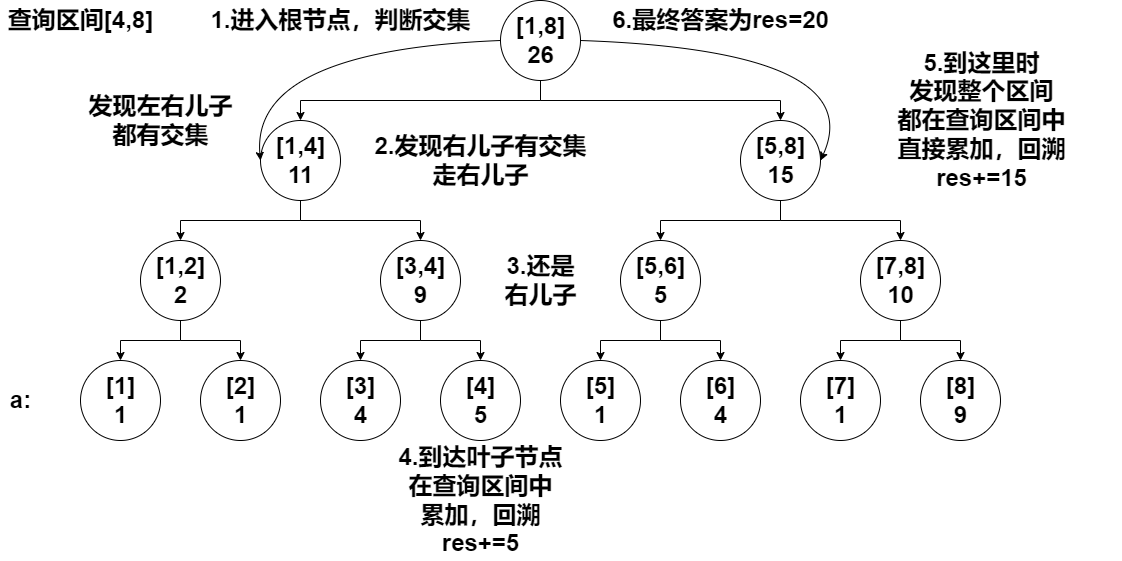
应该步骤写的很清楚了,可以通过代码进一步理解。
T query(int rt,int l,int r){ // l 和 r 表示查询区间!不是当前节点表示区间!
if(l<=t[rt].l && t[rt].r<=r){ // 刚好是查询区间的子集
return t[rt].v; // 直接返回
}
T res=0; // 因为左右儿子都可能去,所以定义一个变量累加
int mid=t[rt].l+t[rt].r>>1;
if(l<=mid) res+=query(ls(rt),l,r); // 若查询区间左端点在左儿子右端点之前,则表示左儿子包含
if(r>mid) res+=query(rs(rt),l,r); // 查询区间右端点在右儿子左端点之后,同上
return res;
}
区间修改
如果直接用单点修改的方法一个一个改,那么时间复杂度就变成 \(\mathcal{O}(n \log n)\) 了。
那我们可不可以参考区间查询的思想呢?一次修改一个区间?那就需要一个叫懒标记的东西了。
懒标记
我们给节点的结构体加一个变量,叫 \(tag\),懒标记的意思。它表示这个节点之下的所有节点的 \(v\) 都需要加上这个 \(tag\)。
这样的话,一次修改一个区间就能实现了:若需修改区间包含某个节点表示的区间,直接将这个节点的 \(tag\) 加上需要增加的值。
可以这样理解懒标记:放寒假了,老师每过一段时间给你布置一次作业(修改一次),你却只是记住有哪些作业(修改懒标记),在开学时(查询)才写(将标记下传)。
除了查询,修改时也需要下传懒标记,节点后代修改(或查询)时需要。
接下来说说如何下传懒标记:
首先一步,就是将懒标记给左右儿子都加上。
还需要修改两个儿子的值,都是修改成儿子表示的区间长度乘上父亲节点的懒标记。因为儿子包含的每一个数都要加上父节点的懒标记,所以要将懒标记乘上长度。
我们将下传懒标记的函数定义为 pushdown():
inline void pushdown(int rt){
t[ls(rt)].tag+=t[rt].tag; // 懒标记传下去
t[ls(rt)].v+=t[rt].tag*(t[ls(rt)].r-t[ls(rt)].l+1); // 修改值
// 右儿子同上
t[rs(rt)].tag+=t[rt].tag;
t[rs(rt)].v+=t[rt].tag*(t[rs(rt)].r-t[rs(rt)].l+1);
t[rt].tag=0; // 记得将父节点的懒标记置 0
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号