QuantLib 金融计算——案例之固息债的关键利率久期（KRD）

QuantLib 金融计算——案例之固息债的关键利率久期（KRD）

2020-11-16 更新：修正 ActualActual 的误用。

QuantLib 金融计算——案例之固息债的关键利率久期（KRD）

概述

作为利率风险系列的第二篇，本文将以《Interest Rate Risk Modeling》为蓝本，介绍关键利率久期（KRD）的基本概念，并依托 QuantLib 展示相关的计算案例。

cover

有关 KRD 的高级内容请见《《Interest Rate Risk Modeling》阅读笔记——第九章》。

关键利率久期的基本概念

上一篇《案例之固息债的价格、久期、凸性和 BPS》中出现的久期和凸性均是基于到期利率（YTM）的风险度量指标。使用 YTM 分析债券隐含了一个重要假设：利率期限结构上各期限的利率同步变化。这个隐含的假设与现实有所出入，尽管期限结构上各期限的利率变化高度相关，但并非 100% 一致。显然，传统的久期无法描述债券价格对期限结构非平行变化的敏感性。

若要更精细地刻画债券关于利率变化的敏感性，需要分别考虑不同期限上利率变化对债券价格的影响，这要求把期限结构本身作为一个动态变量。

一个期限结构其实可以看做是一个无限维的向量，任意一个期限均是一个维度。考虑一个无限维的向量是一个高深的数学问题，然而基于经验观察，期限结构的平滑性相当好，所以只需要选取几个特殊期限作为“锚点”，实践中就可以几乎完全把握整个曲线的变化。

关键利率久期（KRD）就是债券价格关于这些锚点期限上利率的敏感性，一组 KRD 也就描述了债券价格对期限结构非平行变化的敏感性。

从扰动的角度计算 KRD

假设根据当前期限结构算出来的债券价格是 \(P\)，此时某个关键期限 \(K\) 上的利率出现了一个微小的扰动 \(\Delta y\)，扰动出现后重新计算出的债券价格是 \(P^{\prime}\)，那么债券价格关于 \(K\) 期限利率的敏感性就近似是

\[\frac{P^{\prime} - P}{P \times \Delta y} \]

也可以采用精度更高的近似方法，正负扰动对应的价格分别是 \(P^{+}\) 和 \(P^{-}\)，敏感性近似是

\[\frac{P^{+} - P^{-}}{2 P \times \Delta y} \]

为保证期限结构的平滑性，扰动不能只影响一个特定期限，其影响要平滑地扩散到临近的期限。在 KRD 分析中，要求扰动以线性递减的形式扩展到左右相邻的期限，而不会影响相距更远的期限。例如，选定 5、7、10 年三个相邻期限，7 年期上 1 bp 的扰动只能影响到 5 和 10 年期。并且，7-5 年之间，扰动以每年 0.5 bp 的速度递减，7-10 年之间，扰动以每年 1/3 bp 的速度递减。

计算案例

继续以上一篇《案例之固息债的价格、久期、凸性和 BPS》中出现的 200205 为例，计算 2020-07-28 这一天的久期和 KRD。

首先从中国货币网查询债券的基本信息，用以配置 FixedRateBond 对象。

债券起息日：2020-03-10
到期兑付日：2030-03-10
债券期限：10 年
面值(元)：100.00
计息基准：A/A
息票类型：附息式固定利率
付息频率：年
票面利率（%）：3.0700
结算方式：T+1

import QuantLib as ql
import prettytable as pt
import seaborn as sns

today = ql.Date(28, ql.July, 2020)
ql.Settings.instance().evaluationDate = today

settlementDays = 1
faceAmount = 100.0

effectiveDate = ql.Date(10, ql.March, 2020)
terminationDate = ql.Date(10, ql.March, 2030)
tenor = ql.Period(1, ql.Years)
calendar = ql.China(ql.China.IB)
convention = ql.Unadjusted
terminationDateConvention = convention
rule = ql.DateGeneration.Backward
endOfMonth = False

schedule = ql.Schedule(
    effectiveDate,
    terminationDate,
    tenor,
    calendar,
    convention,
    terminationDateConvention,
    rule,
    endOfMonth)

scheduleEx = ql.Schedule(
    effectiveDate,
    ql.Date(10, ql.March, 2031),
    tenor,
    calendar,
    convention,
    terminationDateConvention,
    rule,
    endOfMonth)

coupons = ql.DoubleVector(1)
coupons[0] = 3.07 / 100.0
accrualDayCounter = ql.ActualActual(
    ql.ActualActual.Bond, scheduleEx)
paymentConvention = ql.Unadjusted

bond = ql.FixedRateBond(
    settlementDays,
    faceAmount,
    schedule,
    coupons,
    accrualDayCounter,
    paymentConvention)

在上海清算所查询估值。由于使用的是估值，也就是到期利率，所以当前的期限结构用 FlatForward 类表示。对于水平的期限结构而言，远期利率、即期利率和到期利率三者相等。

bondYield = 3.4124 / 100.0

compounding = ql.Compounded
frequency = ql.Annual

flatCurve = ql.YieldTermStructureHandle(
    ql.FlatForward(
        settlementDays,
        calendar,
        bondYield,
        accrualDayCounter,
        compounding,
        frequency))

计算 KRD 的时候需要向当前的期限结构添加关键期限上的扰动，为此可以借助 QuantLib 中的 InterpolatedPiecewiseZeroSpreadedTermStructure 类模板，它需要一个模板参数 Interpolator，表示所使用的插值方法类。对于 KRD 的计算来说，选择 Linear 作为模板参数，以表示线性插值。

要配置实例化后的类 InterpolatedPiecewiseZeroSpreadedTermStructure<Linear>，需要提供三个核心参数：

一个 Handle<YieldTermStructure> 对象，也就是当前的期限结构，关键期限上的扰动将被施加在此期限结构上；
一列 Handle<Quote> 对象，表示关键期限上的利率扰动；
一列 Date 对象，表示扰动对应的关键期限。

具体到 python 环境下，实例化后的类 InterpolatedPiecewiseZeroSpreadedTermStructure<Linear> 被包装并重命名为 SpreadedLinearZeroInterpolatedTermStructure 类。

在计算 KRD 之前，所有扰动的初始值被设置成零。关键期限有 11 个，分别是 6 个月和 1~10 年，均匀地覆盖每个付息周期。

initValue = 0.0
rate6m = ql.SimpleQuote(initValue)
rate1y = ql.SimpleQuote(initValue)
rate2y = ql.SimpleQuote(initValue)
rate3y = ql.SimpleQuote(initValue)
rate4y = ql.SimpleQuote(initValue)
rate5y = ql.SimpleQuote(initValue)
rate6y = ql.SimpleQuote(initValue)
rate7y = ql.SimpleQuote(initValue)
rate8y = ql.SimpleQuote(initValue)
rate9y = ql.SimpleQuote(initValue)
rate10y = ql.SimpleQuote(initValue)

rate6mHandle = ql.QuoteHandle(rate6m)
rate1yHandle = ql.QuoteHandle(rate1y)
rate2yHandle = ql.QuoteHandle(rate2y)
rate3yHandle = ql.QuoteHandle(rate3y)
rate4yHandle = ql.QuoteHandle(rate4y)
rate5yHandle = ql.QuoteHandle(rate5y)
rate6yHandle = ql.QuoteHandle(rate6y)
rate7yHandle = ql.QuoteHandle(rate7y)
rate8yHandle = ql.QuoteHandle(rate8y)
rate9yHandle = ql.QuoteHandle(rate9y)
rate10yHandle = ql.QuoteHandle(rate10y)

spreads = ql.QuoteHandleVector()
spreads.append(rate6mHandle)
spreads.append(rate1yHandle)
spreads.append(rate2yHandle)
spreads.append(rate3yHandle)
spreads.append(rate4yHandle)
spreads.append(rate5yHandle)
spreads.append(rate6yHandle)
spreads.append(rate7yHandle)
spreads.append(rate8yHandle)
spreads.append(rate9yHandle)
spreads.append(rate10yHandle)

dates = ql.DateVector()
dates.append(flatCurve.referenceDate() + ql.Period(6, ql.Months))
dates.append(flatCurve.referenceDate() + ql.Period(1, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(2, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(3, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(4, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(5, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(6, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(7, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(8, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(9, ql.Years))
dates.append(flatCurve.referenceDate() + ql.Period(10, ql.Years))

termStructure = ql.YieldTermStructureHandle(
    ql.SpreadedLinearZeroInterpolatedTermStructure(
        flatCurve,
        spreads,
        dates,
        compounding,
        frequency,
        accrualDayCounter))

债券定价引擎采用最常见的 DiscountingBondEngine。

engine = ql.DiscountingBondEngine(termStructure)
bond.setPricingEngine(engine)

`Quote` 类和引用带来的便利

在底层 C++ 代码中，QuantLib 类的构造函数和成员函数大量使用了常引用参数和观察者模式，这使得作为参数的对象具有了“穿透性”，参数对象值的改变可以靠引用和观察者模式串联起来的链条影响关联的所有其他对象。

具体到 KRD 的计算，无需重新配置定价引擎，只要改变关键利率的值就可以自动触发债券的计算。

扰动的大小定为 1 bp，调用成员方法 setValue 便可改变 SimpleQuote 对象的值。

duration = ql.BondFunctions.duration(
    bond,
    bondYield,
    accrualDayCounter,
    compounding,
    frequency,
    ql.Duration.Modified)


tab = pt.PrettyTable(['item', 'value'])
tab.add_row(['duration', duration])

# calculate KRDs

bp = 0.01 / 100.0
krdSum = 0.0
krds = []
times = []

# 6m KRD
rate6m.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate6m.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate6m.setValue(initValue)
krd6m = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd6m
krds.append(krd6m)
times.append(0.5)

tab.add_row(['krd6m', krd6m])

# 1y KRD
rate1y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate1y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate1y.setValue(initValue)
krd1y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd1y
krds.append(krd1y)
times.append(1.0)

tab.add_row(['krd1y', krd1y])

# 2y KRD
rate2y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate2y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate2y.setValue(initValue)
krd2y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd2y
krds.append(krd2y)
times.append(2.0)

tab.add_row(['krd2y', krd2y])

# 3y KRD
rate3y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate3y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate3y.setValue(initValue)
krd3y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd3y
krds.append(krd3y)
times.append(3.0)

tab.add_row(['krd3y', krd3y])

# 4y KRD
rate4y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate4y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate4y.setValue(initValue)
krd4y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd4y
krds.append(krd4y)
times.append(4.0)

tab.add_row(['krd4y', krd4y])

# 5y KRD
rate5y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate5y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate5y.setValue(initValue)
krd5y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd5y
krds.append(krd5y)
times.append(5.0)

tab.add_row(['krd5y', krd5y])

# 6y KRD
rate6y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate6y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate6y.setValue(initValue)
krd6y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd6y
krds.append(krd6y)
times.append(6.0)

tab.add_row(['krd6y', krd6y])

# 7y KRD
rate7y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate7y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate7y.setValue(initValue)
krd7y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd7y
krds.append(krd7y)
times.append(7.0)

tab.add_row(['krd7y', krd7y])

# 8y KRD
rate8y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate8y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate8y.setValue(initValue)
krd8y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd8y
krds.append(krd8y)
times.append(8.0)

tab.add_row(['krd8y', krd8y])

# 9y KRD
rate9y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate9y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate9y.setValue(initValue)
krd9y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd9y
krds.append(krd9y)
times.append(9.0)

tab.add_row(['krd9y', krd9y])

# 10y KRD
rate10y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate10y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate10y.setValue(initValue)
krd10y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd10y
krds.append(krd10y)
times.append(10.0)

tab.add_row(['krd10y', krd10y])

tab.add_row(['krdSum', krdSum])

tab.float_format = '.8'

print(tab)

+----------+------------+
|   item   |   value    |
+----------+------------+
| duration | 8.07712202 |
|  krd6m   | 0.01412836 |
|  krd1y   | 0.02182248 |
|  krd2y   | 0.05615594 |
|  krd3y   | 0.08163788 |
|  krd4y   | 0.10535800 |
|  krd5y   | 0.12735475 |
|  krd6y   | 0.14771823 |
|  krd7y   | 0.16683071 |
|  krd8y   | 0.18443629 |
|  krd9y   | 2.84373153 |
|  krd10y  | 4.32794826 |
|  krdSum  | 8.07712244 |
+----------+------------+

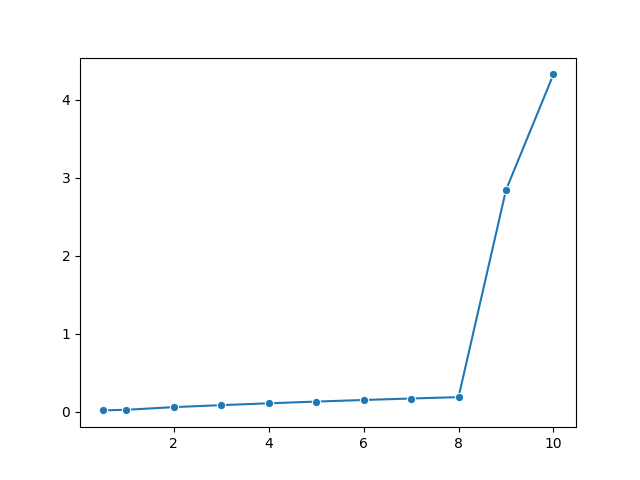
债券最大一笔现金流的剩余期限处在 9～10 年之间，因此 9 和 10 年期利率对债券的影响最大。

理论上，各个 KRD 之和约等于修正久期，这是因为各个关键期限上同时发生扰动的话就相当于曲线发生了平行移动。数值结果正好验证了这一点。

KRD 的曲线图是这样的：

sns.lineplot(
    x=times, y=krds, markers='o')

参考文献

《Interest Rate Risk Modeling》
杨筱燕，《关键利率久期计算及实例分析》

扩展阅读

《QuantLib 金融计算》系列合集

posted @ 2020-08-26 21:14 xuruilong100 阅读(5303) 评论(3) 编辑收藏举报

刷新页面返回顶部

QuantLib 金融计算——案例之固息债的关键利率久期（KRD）

QuantLib 金融计算——案例之固息债的关键利率久期（KRD）

概述

关键利率久期的基本概念

从扰动的角度计算 KRD

计算案例

Quote 类和引用带来的便利

参考文献

扩展阅读

`Quote` 类和引用带来的便利