QuantLib 金融计算——收益率曲线之构建曲线（5）
目录
如果未做特别说明，文中的程序都是 C++11 代码。
QuantLib 金融计算——收益率曲线之构建曲线（5）
本文代码对应的 QuantLib 版本是 1.15。相关源代码可以在 QuantLibEx 找到。
概述
Nelson-Siegel 模型家族的成员一方面可以很好地拟合现实世界中的期限结构，另一方面能够用相当少的参数描述期限结构的复杂形态，并具有明确的经济学含义。目前，QuantLib 只实现了 Nelson-Siegel 模型家族中的两个成员，即 Nelson-Siegel 模型和 Svensson 模型，本文在 QuantLib 的框架内实现 Nelson-Siegel 模型家族中的其他常见成员，并展示如何在拟合过程中添加正则化条件以得到合理的结果。
Nelson-Siegel 模型家族的成员
Nelson-Siegel 模型家族的主要成员之间大同小异，均可以认为是对经典 Nelson-Siegel 模型的小修小改，共同的目标是将即期期限结构表达为几种特定形态期限结构的线性组合（水平、斜率和曲率三种因子）。
经典 Nelson-Siegel 模型以远期利率曲线 \(f(t)\) 为出发点，在连续复利的情境下，认为 \(f(t)\) 可以表示为拉盖尔函数（Laguerre function，\(1,e^{-x},xe^{-x},x^2e^{-x}, \dots\)）的线性组合，再根据即期与远期之间的关系：
\[s(t) = \frac{1}{t} \int_0^t f(s)ds
\]
就可以得到即期期限结构 \(s(t)\) 的表达式，也就是几个函数的线性组合，而这几个函数对应着不同形态的期限结构。
最终对期限结构的拟合就顺理成章地转化为了求解几个待定参数——一个数值优化问题。
Nelson-Siegel 模型
Nelson-Siegel 模型下远期期限结构表示为：
\[f(t) = c_0 + c_1 e^{-\kappa t} + c_2 \kappa t e^{-\kappa t}
\]
对应的即期期限结构表示为：
\[s(t) = c_0 + c_1 \frac{1 - e^{-\kappa t}}{\kappa t} + c_2 \left(\frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t} \right)
\]
其中的三个函数分别对应三个形态的期限结构：
- \(h(t) = 1\)：对应水平的期限结构，即水平因子
- \(h(t) = \frac{1 - e^{-\kappa t}}{\kappa t}\)：对应单调倾斜的期限结构，即斜率因子
- \(h(t) = \frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t}\)：对应中部隆起的期限结构，即曲率因子
参数 \(\kappa\) 则用来控制期限结构的形态。
Svensson 模型
Svensson 模型在 Nelson-Siegel 模型的基础上增加了一项，试图改善对期限结构中段的拟合效果，其远期期限结构表示为：
\[f(t) = c_0 + c_1 e^{-\kappa t} + c_2 \kappa t e^{-\kappa t} + c_3 \kappa_1 t e^{-\kappa_1 t}
\]
对应的即期期限结构表示为：
\[s(t) = c_0 + c_1 \frac{1 - e^{-\kappa t}}{\kappa t} + c_2 \left(\frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t} \right) + c_3 \left(\frac{1 - e^{-\kappa_1 t}}{\kappa_1 t} -e^{-\kappa_1 t} \right)
\]
其中的四个函数分别对应三个形态的期限结构：
- \(h(t) = 1\)：对应水平的期限结构
- \(h(t) = \frac{1 - e^{-\kappa t}}{\kappa t}\)：对应单调倾斜的期限结构
- \(h(t) = \frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t}\)：对应中部隆起的期限结构
- \(h(t) = \frac{1 - e^{-\kappa_1 t}}{\kappa_1 t} -e^{-\kappa_1 t}\)：对应另一个中部隆起的期限结构
参数 \(\kappa\) 和 \(\kappa_1\) 则用来控制期限结构的形态。
修正 Svensson 模型
由于 Svensson 模型存在两个中部隆起的期限结构，形态很相似，致使拟合计算的过程中会受到“共线性”的不良影响。为了克服共线性，有学者直接对即期期限结构动手，修改了第二个中部隆起的期限结构：
\[s(t) = c_0 + c_1 \frac{1 - e^{-\kappa t}}{\kappa t} + c_2 \left(\frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t} \right) + c_3 \left(\frac{1 - e^{-\kappa_1 t}}{\kappa_1 t} -e^{-2\kappa_1 t} \right)
\]
Bjork-Christensen 模型
Bjork-Christensen 模型在 Nelson-Siegel 模型的基础上增加了一项，试图改善对期限结构前段的拟合效果，其远期期限结构表示为：
\[f(t) = c_0 + c_1 e^{-\kappa t} + c_2 \kappa t e^{-\kappa t} + c_3 e^{-2\kappa t}
\]
对应的即期期限结构表示为：
\[s(t) = c_0 + c_1 \frac{1 - e^{-\kappa t}}{\kappa t} + c_2 \left(\frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t} \right) + c_3 \frac{1 - e^{-2\kappa t}}{2\kappa t}
\]
Bliss 模型
Bliss 模型在 Nelson-Siegel 模型上增加了有限的自由度，试图在 Svensson 模型和 Nelson-Siegel 模型之间取得一种折衷，其远期期限结构表示为：
\[f(t) = c_0 + c_1 e^{-\kappa t} + c_2 \kappa_1 t e^{-\kappa_1 t}
\]
对应的即期期限结构表示为：
\[s(t) = c_0 + c_1 \frac{1 - e^{-\kappa t}}{\kappa t} + c_2 \left(\frac{1 - e^{-\kappa_1 t}}{\kappa_1 t} -e^{-\kappa_1 t} \right)
\]
当 \(\kappa = \kappa_1\) 时 Bliss 模型就是 Nelson-Siegel 模型。
Diebold Li 模型
Diebold Li 模型是一个特殊版本的 Nelson-Siegel 模型，用来控制期限结构形态的 \(\kappa\) 需要事先指定，无需估计，远期期限结构表示为：
\[f(t) = c_0 + c_1 e^{-\kappa t} + c_2 \kappa t e^{-\kappa t}
\]
对应的即期期限结构表示为：
\[s(t) = c_0 + c_1 \frac{1 - e^{-\kappa t}}{\kappa t} + c_2 \left(\frac{1 - e^{-\kappa t}}{\kappa t} -e^{-\kappa t} \right)
\]
实现
这几个 Nelson-Siegel 模型家族成员的实现均参照现有的 NelsonSiegelFitting 类，读者可以在 QuantLibEx 找到相关代码。
测试
测试数据
示例所用的样本券交易数据来自专门进行期限结构分析的 R 包——termstrc。具体来说是数据集 govbonds 中的 AUSTRIA 部分，包含 2008-01-30 这一天澳大利亚市场上 16 只固息债的成交数据。读者可以在这里找到对应数据文件。
正则化条件
在拟合期限结构时，QuantLib 支持用户添加 \(L^2\) 正则化条件，为此用户需要提供两个数组，分别是
- 猜想的参数
guess：\(\beta^{guess}\) - 正则化权重
l2：\(\lambda(>0)\)
加入正则化条件之后，期限结构的拟合可以表述为如下数值优化问题：
\[\mathop{\arg\min}_{\beta} F(\beta) := \sum_j \left(ModelPrice_j(s(t;\beta)) - MarketPrice_{j} \right)^2 + \sum_i\lambda_i(\beta_i - \beta^{guess}_i)^2
\]
通常相邻两个时间点上期限结构的参数不会发生剧烈变化，因此猜想的参数 \(\beta^{guess}\) 可以设置为上一期的结果，正则化权重 \(\lambda\) 的设置就见仁见智了。
代码
void TestNelsonSiegelClassTermStructure() {
using namespace std;
using namespace QuantLib;
/*
基础交易数据
*/
Size bondNum = 16;
vector<Real> cleanPrice = {
100.4941, 103.5572, 104.4135, 105.0056, 99.8335, 101.25, 102.3832, 97.0053,
99.5164, 101.2435, 104.0539, 101.15, 96.1395, 91.1123, 122.0027, 92.4369};
vector<Handle<Quote>> priceHandle(bondNum);
for (Size i = 0; i < bondNum; ++i) {
ext::shared_ptr<Quote> q(
new SimpleQuote(cleanPrice[i]));
Handle<Quote> hq(q);
priceHandle[i] = hq;
}
vector<Year> issueYear = {
1999, 1999, 2001, 2002, 2003, 1999, 2004, 2005,
2006, 2007, 2003, 2008, 2005, 2006, 1997, 2007};
vector<Month> issueMonth = {
Feb, Oct, Jan, Jan, May, Jan, Jan, Apr,
Apr, Sep, Jan, Jan, Jan, Jan, Jul, Jan};
vector<Day> issueDay = {
22, 22, 4, 9, 20, 15, 15, 26, 21, 17, 15, 8, 14, 11, 10, 12};
vector<Year> maturityYear = {
2009, 2010, 2011, 2012, 2013, 2014, 2014, 2015,
2016, 2017, 2018, 2019, 2020, 2021, 2027, 2037};
vector<Month> maturityMonth = {
Jul, Jan, Jan, Jul, Oct, Jan, Jul, Jul,
Sep, Sep, Jan, Mar, Jul, Sep, Jul, Mar};
vector<Day> maturityDay = {
15, 15, 4, 15, 20, 15, 15, 15,
15, 15, 15, 15, 15, 15, 15, 15};
vector<Date> issueDate(bondNum), maturityDate(bondNum);
for (Size i = 0; i < bondNum; ++i) {
Date idate(issueDay[i], issueMonth[i], issueYear[i]);
Date mdate(maturityDay[i], maturityMonth[i], maturityYear[i]);
issueDate[i] = idate;
maturityDate[i] = mdate;
}
vector<Real> couponRate = {
0.04, 0.055, 0.0525, 0.05, 0.038, 0.04125, 0.043, 0.035,
0.04, 0.043, 0.0465, 0.0435, 0.039, 0.035, 0.0625, 0.0415};
/*
配置 helper
*/
Frequency frequency = Annual;
Actual365Fixed dayCounter(Actual365Fixed::Standard);
BusinessDayConvention paymentConv = Unadjusted;
BusinessDayConvention terminationDateConv = Unadjusted;
BusinessDayConvention convention = Unadjusted;
Real redemption = 100.0;
Real faceAmount = 100.0;
Australia calendar;
Date today = calendar.adjust(Date(30, Jan, 2008));
Settings::instance().evaluationDate() = today;
Natural bondSettlementDays = 0;
Date bondSettlementDate = calendar.advance(
today,
Period(bondSettlementDays, Days));
vector<ext::shared_ptr<BondHelper>> instruments(bondNum);
vector<Time> maturity(bondNum);
for (Size i = 0; i < bondNum; ++i) {
vector<Real> bondCoupon = {couponRate[i]};
Schedule schedule(
issueDate[i],
maturityDate[i],
Period(frequency),
calendar,
convention,
terminationDateConv,
DateGeneration::Backward,
false);
ext::shared_ptr<FixedRateBondHelper> helper(
new FixedRateBondHelper(
priceHandle[i],
bondSettlementDays,
faceAmount,
schedule,
bondCoupon,
dayCounter,
paymentConv,
redemption));
maturity[i] = dayCounter.yearFraction(
bondSettlementDate, helper->maturityDate());
instruments[i] = helper;
}
Real accuracy = 1.0e-6;
Natural maxEvaluations = 5000;
Array weights;
/*
正则化条件
*/
Array l2Ns(4, 0.5);
Array guessNs(4);
guessNs[0] = 4 / 100.0, guessNs[1] = 0.0, guessNs[2] = 0.0, guessNs[3] = 0.5;
Array l2Sv(6, 0.5);
Array guessSv(6);
guessSv[0] = 4 / 100.0, guessSv[1] = 0.0, guessSv[2] = 0.0, guessSv[3] = 0.0, guessSv[4] = 0.2, guessSv[5] = 0.15;
Array l2Asv(6, 0.5);
Array guessAsv(6);
guessAsv[0] = 4 / 100.0, guessAsv[1] = 0.0, guessAsv[2] = 0.0, guessAsv[3] = 0.0, guessAsv[4] = 0.2, guessAsv[5] = 0.3;
Array l2Bc(5, 0.5);
Array guessBc(5);
guessBc[0] = 4 / 100.0, guessBc[1] = 0.0, guessBc[2] = 0.0, guessBc[3] = 0.0, guessBc[4] = 0.2;
Array l2Bl(5, 0.5);
Array guessBl(5);
guessBl[0] = 4 / 100.0, guessBl[1] = 0.0, guessBl[2] = 0.0, guessBl[3] = 0.5, guessBl[4] = 0.5;
ext::shared_ptr<OptimizationMethod> optMethod(
new LevenbergMarquardt());
/*
拟合方法
*/
NelsonSiegelFitting nsf(
weights, optMethod, l2Ns);
SvenssonFitting svf(
weights, optMethod, l2Sv);
AdjustedSvenssonFitting asvf(
weights, optMethod, l2Asv);
DieboldLiFitting dlf(
0.5, weights, optMethod);
BjorkChristensenFitting bcf(
weights, optMethod, l2Bc);
BlissFitting blf(
weights, optMethod, l2Bl);
FittedBondDiscountCurve tsNelsonSiegel(
bondSettlementDate,
instruments,
dayCounter,
nsf,
accuracy,
maxEvaluations,
guessNs);
FittedBondDiscountCurve tsSvensson(
bondSettlementDate,
instruments,
dayCounter,
svf,
accuracy,
maxEvaluations,
guessSv);
FittedBondDiscountCurve tsAdjustedSvensson(
bondSettlementDate,
instruments,
dayCounter,
asvf,
accuracy,
maxEvaluations,
guessAsv);
FittedBondDiscountCurve tsDieboldLi(
bondSettlementDate,
instruments,
dayCounter,
dlf,
accuracy,
maxEvaluations);
FittedBondDiscountCurve tsBjorkChristensen(
bondSettlementDate,
instruments,
dayCounter,
bcf,
accuracy,
maxEvaluations,
guessBc);
FittedBondDiscountCurve tsBliss(
bondSettlementDate,
instruments,
dayCounter,
blf,
accuracy,
maxEvaluations,
guessBl);
/*
结果
*/
cout << "NelsonSiegel Results: \t\t" << tsNelsonSiegel.fitResults().solution() << endl;
cout << "Svensson Results: \t\t" << tsSvensson.fitResults().solution() << endl;
cout << "AdjustedSvensson Results: \t" << tsAdjustedSvensson.fitResults().solution() << endl;
cout << "DieboldLi Results: \t\t" << tsDieboldLi.fitResults().solution() << endl;
cout << "BjorkChristensen Results: \t" << tsBjorkChristensen.fitResults().solution() << endl;
cout << "Bliss Results: \t\t\t" << tsBliss.fitResults().solution() << endl;
cout << endl;
Real NSrate, SVrate, ASVrate, DLrate, BCrate, Brate;
for (Size i = 0; i < bondNum; ++i) {
Time t = dayCounter.yearFraction(
bondSettlementDate, maturityDate[i]);
NSrate = tsNelsonSiegel.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;
SVrate = tsSvensson.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;
ASVrate = tsAdjustedSvensson.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;
DLrate = tsDieboldLi.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;
BCrate = tsBjorkChristensen.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;
Brate = tsBliss.zeroRate(t, Compounding::Continuous, frequency).rate() * 100.0;
cout << setprecision(3) << fixed
<< t << ",\t"
<< NSrate << ",\t"
<< SVrate << ",\t"
<< ASVrate << ",\t"
<< DLrate << ",\t"
<< BCrate << ",\t"
<< Brate << endl;
}
}
拟合结果
NelsonSiegel Results: [ 0.0500803; -0.0105414; -0.0303842; 0.456529 ]
Svensson Results: [ 0.0431095; -0.00716036; -0.0340932; 0.0391339; 0.228995; 0.117208 ]
AdjustedSvensson Results: [ 0.0506269; -0.0116339; 0.0029305; -0.0135686; 0.179066; 0.267767 ]
DieboldLi Results: [ 0.0496643; -0.00879931; -0.0329267 ]
BjorkChristensen Results: [ 0.0508039; -0.0555185; 0.0115282; 0.0415581; 0.227838 ]
Bliss Results: [ 0.0500892; -0.0106013; -0.0315605; 0.513831; 0.456329 ]
1.458, 3.581, 3.544, 3.569, 3.592, 3.547, 3.581
1.962, 3.545, 3.550, 3.542, 3.542, 3.543, 3.545
2.932, 3.549, 3.585, 3.554, 3.537, 3.573, 3.549
4.460, 3.657, 3.682, 3.664, 3.651, 3.678, 3.657
5.726, 3.780, 3.782, 3.782, 3.780, 3.786, 3.780
5.964, 3.803, 3.802, 3.805, 3.805, 3.807, 3.803
6.460, 3.852, 3.843, 3.852, 3.856, 3.850, 3.852
7.460, 3.947, 3.928, 3.943, 3.954, 3.936, 3.947
8.633, 4.049, 4.024, 4.042, 4.057, 4.031, 4.049
9.633, 4.126, 4.102, 4.117, 4.134, 4.106, 4.126
9.967, 4.150, 4.127, 4.141, 4.157, 4.129, 4.150
11.129, 4.226, 4.210, 4.217, 4.232, 4.206, 4.226
12.466, 4.302, 4.295, 4.293, 4.305, 4.284, 4.301
13.636, 4.358, 4.360, 4.351, 4.359, 4.344, 4.358
19.468, 4.548, 4.576, 4.553, 4.538, 4.555, 4.548
29.142, 4.700, 4.677, 4.721, 4.680, 4.730, 4.701
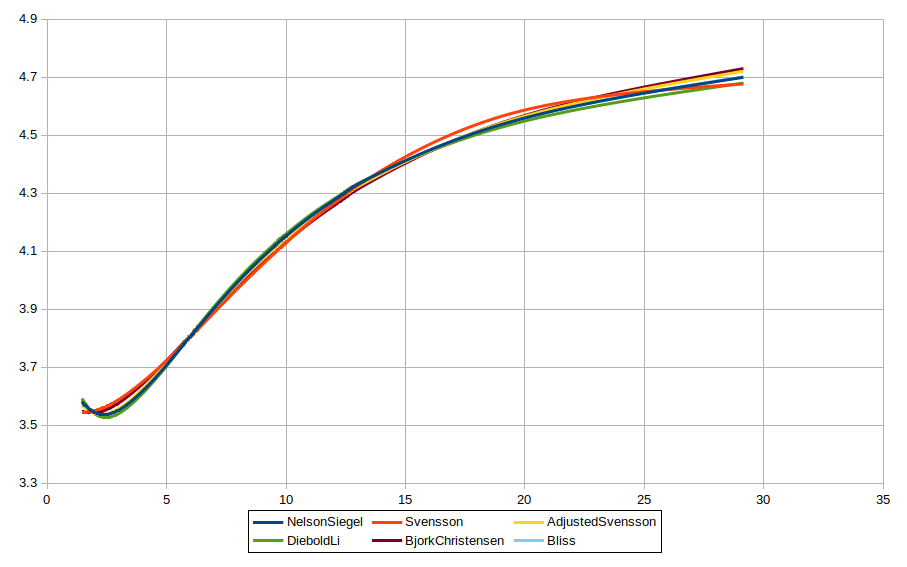
拟合结果大致分为两组，
- 第一组，Svensson 模型和 Bjork-Christensen 模型在前段的形态相互比较接近，
- 第二组，其他几个模型在前段的形态相互比较接近
后续话题
如果没有正则化约束，当控制曲线形状的参数已知时，Nelson-Siegel 模型和 Svensson 模型的拟合问题是凸的（Ferstl & Hayden, 2010），比较容易解决。但参数未知时，问题变成了非凸的。
在没有正则化约束的条件下如何找到合理的模型参数将成为后续的话题。
参考文献
- Ferstl.R, Hayden.J (2010). "Zero-Coupon Yield Curve Estimation with the Package
termstrc." Journal of Statistical Software, Volume 36, Issue 1. - De Pooter M (2007). "Examining the Nelson-Siegel Class of Term Structure Models: In-Sample Fit versus Out-of-Sample Forecasting Performance." SSRN eLibrary. http://ssrn.com/paper=992748.
扩展阅读
★ 持续学习 ★ 坚持创作 ★
