OpenMVG 系列 (2)：图像和数值运算

OpenMVG 的功能模块由若干核心库组成，本文主要介绍 image 和 numeric 两个库

1 图像库

图像库包含图像容器 Image<T>、图像IO读写函数 ReadImage() 和 WriteImage()、基本绘图操作 DrawLine()、DrawCircle() 和 DrawEllipse() 等

1.1 图像容器

Image<T> 是一个图像类泛型容器，T 代表像素类型，可以是单通道的灰度图

  // 8bit and 32bit gray images
  Image<unsigned char> gray_img_8bit;  
  Image<double> gray_img_32bit;

也可以是 RGB 和 RGBA 等多通道的彩色图

  Image<Rgb<unsigned char>>  rgb_img_8bit;   // 8bit RGB
  Image<Rgb<double> >        rgb_img_32bit;  // 32bit RGB

  Image<Rgba<unsigned char> > rgba_img_8bit;  // 8bit RGBA

Image<T> 也是一个模板类，继承自 Eigen 中的“行优先”模板类 Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>，所谓“行优先”，指的是矩阵内元素的存储顺序

以 $A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$ 为例，行优先时元素在内存中的存储顺序为 1-2-3-4-5-6，列优先为 1-4-2-5-3-6

  template <typename T>
  class Image : public Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>
  {
      // ...
  };

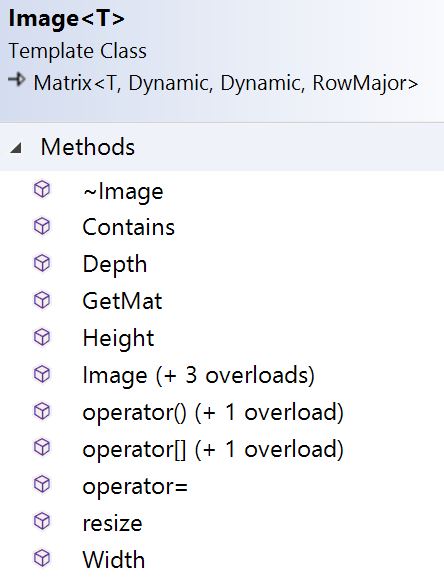
Image<T> 的完整类视图如下，包含构造函数、析构函数、运算符重载函数、获取高度(行)函数等

1.2 读写操作

图像的 IO 读写函数，使用比较简单，如下：

  // Read a grayscale image
  Image<unit8_t> gray_img;
  bool bRet = ReadImage("Foo.imgExtension", &gray_img);

  // Read a color image
  Image<RGBColor> rgb_img;
  bool bRet = ReadImage("Foo.imgExtension", &rgb_img);

图像 IO 读写函数的实现，稍微复杂，要根据不同的图像格式 (如 jpeg、tiff、png等)，调用各自的库来实现 (如 libjpeg、libpng、libtiff 等)，ReadImage() -> ReadJpg() -> ReadJpgStream() -> libjpeg

笔者刚接触图像处理时，并不知道 libjpeg 等库的存在，曾花了不少时间，尝试用 c 语言读写 jpeg 图片，现在看来是浪费了时间，并无多大的用处

在此摘录 OpenMVG 中 ReadJpgStream() 的实现代码，仅供阅读参考，希望不要投入过多精力

int ReadJpgStream(FILE * file, std::vector<unsigned char> * ptr, int * w, int * h, int * depth) 
{
  jpeg_decompress_struct cinfo;
  struct my_error_mgr jerr;
  cinfo.err = jpeg_std_error(&jerr.pub);
  jerr.pub.error_exit = &jpeg_error;

  if (setjmp(jerr.setjmp_buffer)) {
    std::cerr << "Error JPG: Failed to decompress.";
    jpeg_destroy_decompress(&cinfo);
    return 0;
  }

  jpeg_create_decompress(&cinfo);
  jpeg_stdio_src(&cinfo, file);
  jpeg_read_header(&cinfo, TRUE);
  jpeg_start_decompress(&cinfo);

  int row_stride = cinfo.output_width * cinfo.output_components;

  *h = cinfo.output_height;
  *w = cinfo.output_width;
  *depth = cinfo.output_components;
  ptr->resize((*h)*(*w)*(*depth));

  unsigned char *ptrCpy = &(*ptr)[0];

  while (cinfo.output_scanline < cinfo.output_height) {
    JSAMPROW scanline[1] = { ptrCpy };
    jpeg_read_scanlines(&cinfo, scanline, 1);
    ptrCpy += row_stride;
  }

  jpeg_finish_decompress(&cinfo);
  jpeg_destroy_decompress(&cinfo);
  return 1;
}

2 数值运算

numeric 的实现，主要是基于开源的 C++ 模板库 Eigen，它包含了线性代数的基本运算：向量、矩阵、矩阵运算等

2.1 向量和矩阵

Vec2f 和 Vec2 分别表示类型为 float 和 double 的 2d 点 (x, y)

  // 2d vector using float internal format
  using Vec2f = Eigen::Vector2f;

  // 2d vector using double internal format
  using Vec2 = Eigen::Vector2d;

Vec3f 和 Vec3 分别表示类型为 float 和 double 的 3d 点 (x, y, z)

  // 3d vector using float internal format
  using Vec3f =Eigen::Vector3f;

  // 3d vector using double internal format
  using Vec3 = Eigen::Vector3d;

Mat 表示一个通用的矩阵，Mat2X 是列存储形式的一组 2d 点，Mat3X 则是列存储形式的一组 3d 点

  // Unconstrained matrix using double internal format
  using Mat = Eigen::MatrixXd;

  // 2xN matrix using double internal format
  using Mat2X = Eigen::Matrix<double, 2, Eigen::Dynamic>;

  // 3xN matrix using double internal format
  using Mat3X = Eigen::Matrix<double, 3, Eigen::Dynamic>;

2.2 奇异值分解 - SVD

SVD 将一个矩阵分解成三个矩阵的乘积 $ A_{m \times n} = UDV^T$，其中，$U_{m\times m}$ 和 $V_{n \times n}$ 都是正交矩阵， $D_{m \times n}$ 是对角矩阵

在图像的几何变换中，仿射变换可视为一个奇异值分解的过程，参见博文 OpenCV 之图像几何变换

变换过程如下：

$\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} \sigma_{1} & \\ & \sigma_2 \end{bmatrix} \begin{bmatrix} \cos \phi & sin \phi \\ -\sin \phi & \cos \phi \end{bmatrix} = UDV^T$

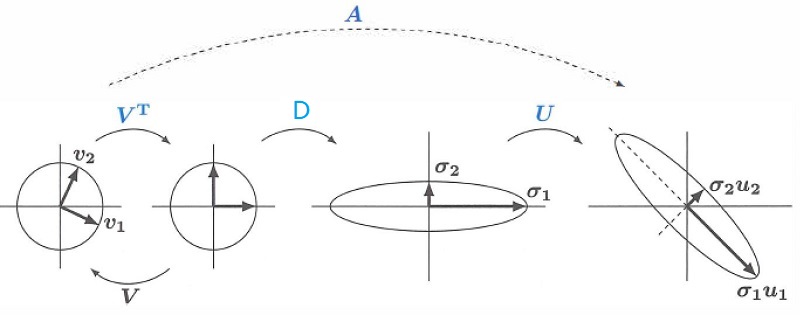
更为形象的描述：第1个圆旋转 $V^T$得到第2个圆，再经过 $D$ 的拉伸得到第3个椭圆，最后旋转 $U$ 得到第4个椭圆

2.3 代码示例

Eigen 中的 SVD 分解：

  MatrixXf A = MatrixXf(3, 2);
  A << -1, -0.0827, -0.737, 0.0655, 0.511, -0.562;
  cout << "The matrix A:" << endl << A << endl;

  // SVD decomposition
  JacobiSVD<MatrixXf> svd(A, ComputeFullU | ComputeFullV);

  cout << "Singular values are:" << endl << svd.singularValues() << endl;
  cout << "Left singular vectors U :" << endl << svd.matrixU() << endl;
  cout << "Right singular vectors Vt :" << endl << svd.matrixV() << endl;

OpenCV 中的 SVD 分解：SVDecomp (InputArray src, OutputArray w, OutputArray u, OutputArray vt, int flags = 0)

Mat W, U, Vt;
Mat A = (Mat_<float>(3, 2) << -1, - 0.0827, -0.737, 0.0655, 0.511, -0.562);
SVDecomp(A, W, U, Vt, SVD::FULL_UV);

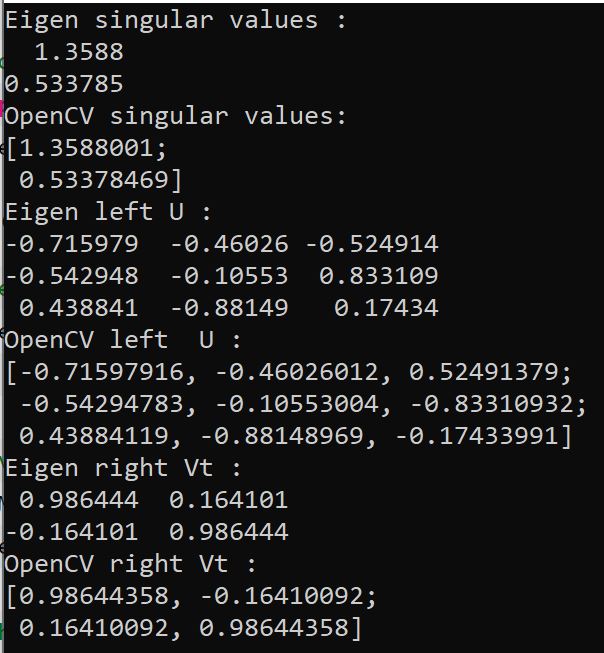
从结果来看，Eigen 和 OpenCV 的 SVD 分解，有两处细微差异：一是小数点后位数不同，二是 U 和 Vt 中，部分元素的符号不同

3 Image 与 cv::Mat

OpenCV 中也有一个表示图像容器的模板类 Mat，参见博文 OpenCV 之 Mat 类，二者的转换关系如下：

1）cv::Mat 转换为 Image (灰度图)

  // cv Mat -> mvg Image
  cv::Mat img_cv = cv::imread("messi.jpg", cv::IMREAD_GRAYSCALE);

  Image<uint8_t> img_mvg;
  img_mvg.resize(img_cv.cols, img_cv.rows);

  // convert and save
  cv::cv2eigen(img_cv, *(Image<uint8_t>::Base*) &img_mvg);
  WriteImage("messi_mvg.jpg", img_mvg);

2）cv::Mat 转换为 Image (彩色图)

  cv::Mat img_cv;
  img_cv = cv::imread("messi.jpg");

  Image<RGBColor> img_mvg;
  img_mvg.resize(img_cv.cols, img_cv.rows);
  cv::cvtColor(img_cv, img_cv, cv::COLOR_BGR2RGB);

  // convert and save 
  memcpy(img_mvg.data(), static_cast<unsigned char*>(img_cv.data), img_cv.cols * img_cv.rows * 3);
  WriteImage("messi_mvg.jpg", img_mvg);

3）Image 转换为 cv::Mat

  // Read a grayscale image
  Image<unsigned char> img_mvg;
  bool bRet = ReadImage("messi.jpg", &img_mvg);

  // mvg Image -> cv Mat
  cv::Mat img_cv;
  cv::eigen2cv(img_mvg.GetMat(), img_cv);

  // show image
  cv::imshow("messi", img_cv);
  cv::waitKey();

转换后的图片结果：