题组|数学思维的层次递进

前言

在数学思维的培养和提升过程中，数学题组的建设，应该说有很大的帮助。各位可以利用下例体会一下。本博文也是用例子说明如何学习数学的问题。

题组案例1

• 〔对勾函数题组〕以下的题目是按照函数的难以程度，题目涉及到的知识点的多少排列，其求解难度也是由易到难；对勾型函数

[高一新课使用]已知函数\(f(x)=x+\cfrac{2}{x}\)，\(x\in (0,4)\)，求函数\(f(x)\)的最小值；

预备知识：对勾函数\(f(x)=x+\cfrac{2}{x}\)，\(x\in (0,4)\)，

则\(x\in (0,\sqrt{2}]\)上单调递减，\(x\in (\sqrt{2},4)\)上单调递增，

故\(f(x)_{min}=f(\sqrt{2})=2\sqrt{2}\)；

[高一新课使用]已知函数\(f(x)=x+\cfrac{2}{x}\)，\(x\in [\cfrac{1}{4},3]\)，求函数\(f(x)\)的最值；

分析：由上例可知[此例是限定区间]，函数在\([\cfrac{1}{4},\sqrt{2}]\)上单调递减，在\([\sqrt{2},3]\)上单调递增，如图所示，

故\(f(x)_{\min}=f(\sqrt{2})=2\sqrt{2}\)；

\(f(x)_{\max}=\max\{f(\cfrac{1}{4})，f(3)\}=8\cfrac{1}{4}=\cfrac{25}{4}\)；

[高一高二使用]已知函数\(f(x)=x^2+\cfrac{2}{x^2}\)，\(x\in (0,\sqrt{2})\)，求函数\(f(x)\)的最小值；

提示：和引例2相比，仅仅多增加了考点：使用换元法，

令\(x^2=t\)，则由\(x\in (0,\sqrt{2})\)，得到\(x^2=t\in (0,2)\)，

故问题转化为已知函数\(g(t)=t+\cfrac{2}{t}\)，\(t\in (0,2)\)，求函数\(g(t)\)的最小值；仿上例完成即可；

[高三一轮使用]已知函数\(f(x)=x^2-ax+2>0\)在\(x\in (0,\sqrt{2})\)上恒成立，求参数\(a\)的取值范围；

提示：和引例2相比，多增加了考点：不等式恒成立模型和分离参数法，由于\(x\in (0,\sqrt{2})\)

则分离参数得到，\(a<\cfrac{x^2+2}{x}\)，即\(a<x+\cfrac{2}{x}\)在\(x\in (0,\sqrt{2})\)上恒成立，

令\(x+\cfrac{2}{x}=h(x)\)，\(x\in (0,\sqrt{2})\)，仿上求其最小值或最小值 极限 即可。

由于\(x\in (0,\sqrt{2})\)，\(f(x)> f(\sqrt{2})=2\sqrt{2}\)，故\(a\leqslant 2\sqrt{2}\).

[高三专题拟使用]已知命题“当\(x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2>0\)为真命题”，求参数\(a\)的取值范围；

提示：和引例2相比，多增加了考点：命题的真假判断，转化与划归，恒成立命题模型，分离参数法；

由于当\(x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2>0\)为真命题，

故函数\(f(x)=x^2-ax+2>0\)在\(x\in (0,\sqrt{2})\)时恒成立，分离参数得到

\(a<\cfrac{x^2+2}{x}\)，即\(a<x+\cfrac{2}{x}\)在\(x\in (0,\sqrt{2})\)上恒成立，

令\(x+\cfrac{2}{x}=h(x)\)，\(x\in (0,\sqrt{2})\)，仿上求其最小值或最小值 极限 即可。

由于\(x\in (0,\sqrt{2})\)，\(f(x)> f(\sqrt{2})=2\sqrt{2}\)，故\(a\leqslant 2\sqrt{2}\).

[高三专题拟使用]若命题“\(\exists x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2\leqslant 0\)为假命题”，求参数\(a\)的取值范围；

提示：本题目多增加了考点：全称命题和特称命题的否定，恒成立命题模型，分离参数法；

原命题[特称命题]为假命题，则该命题的否定[全称命题]为真命题；

由题目可知，\(\not\exists x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2\leqslant 0\)能成立，

则命题“当\(\forall x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2>0\)为真命题”，至此，仿引例5完成；

[高三专题拟使用]若命题“当\(x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2>0\)为假命题”，求参数\(a\)的取值范围；

提示：本题目多增加了考点：全称命题和特称命题的否定，能成立模型，转化与划归，分离参数，

由题目可知，命题“\(\forall x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2>0\)为假命题”，[全称命题，假命题]

则命题“\(\exists x\in (0,\sqrt{2})\)时，函数\(f(x)=x^2-ax+2\leqslant0\)为真命题”，[特称命题，真命题]

即函数\(f(x)=x^2-ax+2\leqslant 0\)在\(x\in (0,\sqrt{2})\)时能成立；分离参数得到，

\(a\geqslant \cfrac{x^2+2}{x}\)，即\(a\geqslant x+\cfrac{2}{x}\)在\(x\in (0,\sqrt{2})\)上能成立，

令\(x+\cfrac{2}{x}=h(x)\)，\(x\in (0,\sqrt{2})\)，仿上求其最小值或最小值极限即可。

由于\(x\in (0,\sqrt{2})\)，\(f(x)> f(\sqrt{2})=2\sqrt{2}\)， 故\(a> 2\sqrt{2}\). 解释

[高考模拟考试拟使用]若命题\(“\exists x\in (0,2]\)，不等式\(e^{2x}+e^{-2x}-a(e^x-e^{-x})<0”\)为假命题，求参数\(a\)的取值范围；

提示：和引例7相比，多增加了考点：函数的储备和函数的变形运算；

[知识储备回顾：注意函数\(y=e^x-e^{-x}\)在\(x\in (0,2]\)上单调递增且恒为正]

由题可知，命题\(“\forall x\in (0,2]\)，不等式\(e^{2x}+e^{-2x}-a(e^x-e^{-x})\geqslant 0”\)为真命题，

即\((e^x-e^{-x})a\leqslant e^{2x}+e^{-2x}\)在\(x\in (0,2]\)上恒成立，

即\(a\leqslant \cfrac{e^{2x}+e^{-2x}}{e^x-e^{-x}}\)在\(x\in (0,2]\)上恒成立，

令\(\cfrac{e^{2x}+e^{-2x}}{e^x-e^{-x}}=g(x)\)，需要求解函数\(g(x)\)的最小值或最小值的极限；

化简得到，\(g(x)=\cfrac{e^{2x}+e^{-2x}}{e^x-e^{-x}}=\cfrac{(e^{x}-e^{-x})^2+2}{e^x-e^{-x}}\)

\(=e^x-e^{-x}+\cfrac{2}{e^x-e^{-x}}\)，

令\(t=e^x-e^{-x}\)，由于\(x\in (0,2]\)时函数\(t=e^x-e^{-x}\)单调递增，则\(t\in (0,e^2-e^{-2}]\)，

则函数\(g(x)=h(t)=t+\cfrac{2}{t}\)，\(t\in (0,e^2-e^{-2}]\)，

由上述储备可知，函数\(h(t)\)在区间\((0,\sqrt{2}]\)上单调递减，在区间\([\sqrt{2},e^2-e^{-2}]\)上单调递增，

故\(g(x)_{\min}=h(t)_{\min}=h(\sqrt{2})=2\sqrt{2}\)，

故\(a\leqslant 2\sqrt{2}\)，即所求的\(a\)的取值范围为\((-\infty,2\sqrt{2}]\)；

解后反思：当得到\(g(x)=e^x-e^{-x}+\cfrac{2}{e^x-e^{-x}}\)，自然还可以使用均值不等式来求解最小值；

[高考模拟考试拟使用]若命题\(“\exists x\in (0,2]\)，不等式\(e^{2x}+e^{-2x}-a(e^x+e^{-x})<0”\)为假命题，求参数\(a\)的取值范围；

提示：和引例8相比，本题仅仅是函数形式的不同和储备函数的不同；

[知识储备回顾：注意函数\(y=e^x+e^{-x}\)在\(x\in (0,2]\)上单调递增且恒为正]

由题可知，命题\(“\forall x\in (0,2]\)，不等式\(e^{2x}+e^{-2x}-a(e^x+e^{-x})\geqslant 0”\)为真命题，

即\((e^x+e^{-x})a\leqslant e^{2x}+e^{-2x}\)在\(x\in (0,2]\)上恒成立，

即\(a\leqslant \cfrac{e^{2x}+e^{-2x}}{e^x+e^{-x}}\)在\(x\in (0,2]\)上恒成立，

令\(\cfrac{e^{2x}+e^{-2x}}{e^x+e^{-x}}=h(x)\)，需要求解函数\(h(x)\)的最小值或最小值的极限；

化简得到，\(h(x)=\cfrac{e^{2x}+e^{-2x}}{e^x+e^{-x}}=\cfrac{(e^{x}+e^{-x})^2-2}{e^x+e^{-x}}\)

\(=e^x+e^{-x}-\cfrac{2}{e^x+e^{-x}}\)，

令\(t=e^x+e^{-x}\)，由于\(x\in (0,2]\)时函数\(t=e^x+e^{-x}\)单调递增，则\(t\in (2,e^2+e^{-2}]\)，

则函数\(h(x)=m(t)=t-\cfrac{2}{t}\)，\(t\in (2,e^2+e^{-2}]\)，

函数\(h(t)\)在区间\((2,e^2+e^{-2}]\)上单调递增，

故\(h(x)_{\min}=m(t)_{\min}\rightarrow m(2)=2-\cfrac{2}{2}=1\)，

即所求的\(a\)的取值范围为\((-\infty,1]\)；

题组案例2

函数与导数相关

(已知单调性求参数的取值范围)已知函数\(f(x)=x^3-ax-1\)，

(1).讨论函数\(f(x)\)的单调性；

分析：用导数法求解，\(f'(x)=3x^2-a\) ，作出导函数的简图(三种代表情形)，

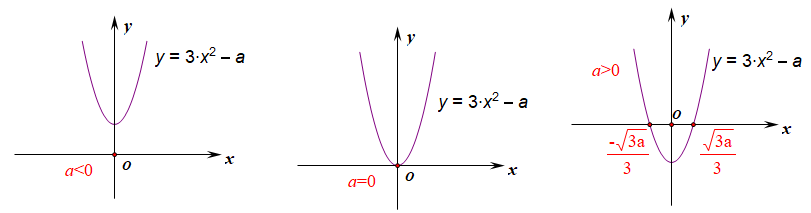
当\(a\leq 0\)时，\(f'(x)\ge 0\)，故在\((-\infty，+\infty)\)上单调递增；

当\(a>0\)时，令\(f'(x)=0\)，得到\(x=\pm \cfrac{\sqrt{3a}}{3}\)，故\(x\in (-\infty， -\cfrac{\sqrt{3a}}{3})\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；

\(x\in (-\cfrac{\sqrt{3a}}{3}，\cfrac{\sqrt{3a}}{3})\)时，\(f'(x)<0\)，\(f(x)\searrow\)；\(x\in (\cfrac{\sqrt{3a}}{3}，+\infty)\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；

(2).若函数\(f(x)\)在\(R\)上是增函数，求\(a\)的取值范围。

分析：由于函数\(f(x)\)在\(R\)上是增函数，即\(f'(x)\geqslant 0\)在\(R\)上恒成立，且恒满足\(f'(x)\neq 0\)，即\(f(x)\)不为常函数；

则\(f'(x)=3x^2-a\geqslant 0\)恒成立，分离参数得到，

\(a\leqslant 3x^2\)在\(R\)上恒成立，而\((3x^2)_{min}=0\)，

则\(a\leqslant 0\)，又因为当\(a=0\)时，函数不为常函数，故参数\(a\)的取值范围是\(a\in (-\infty,0]\)。

函数\(f(x)=x^3-ax-1\)，若函数\(f(x)\)在\((1，+\infty)\)上是增函数，求\(a\)的取值范围。

分析： \(f'(x)=3x^2-a\ge 0\)在\((1，+\infty)\)上恒成立，故\(a\leq 3x^2\)在\((1，+\infty)\)上恒成立，需要求\(y=3x^2\)在\((1，+\infty)\)上的最小值或者最小值极限为3，故有\(a\leq 3\)；

函数\(f(x)=x^3-ax-1\)，若函数\(f(x)\)在\((-1，1)\)上是减函数，求\(a\)的取值范围。

分析： \(f'(x)=3x^2-a\leq 0\)在\((-1，1)\)上恒成立，

故\(a\ge 3x^2\)在\((-1，1)\)上恒成立，

需要求\(y=3x^2\)在\((-1，1)\)上的最大值或者最大值极限为3，故有\(a\ge 3\)；

[恰成立命题]函数\(f(x)=x^3-ax-1\)，若函数\(f(x)\)的单调递减区间是\((-1，1)\)，求\(a\)的值。

分析：由第一问可知函数在\((-\cfrac{\sqrt{3a}}{3}，\cfrac{\sqrt{3a}}{3})\)上单调递减，

现已知单调递减区间是\((-1，1)\)，故有两个区间相等，

即\(\cfrac{\sqrt{3a}}{3}=1\)，解得\(a=3\)；

函数\(f(x)=x^3-ax-1\)，若函数\(f(x)\)在\((-1，1)\)上不单调，求\(a\)的取值范围。

解法1：补集思想，由上述解题过程可知

当单增时，\(a\leq 0\)；当单减时，\(a\ge 3\)，故其补集则\(0<a<3\)时必然不单调。

故\(a\)的取值范围为\(a\in (0，3)\)。

解法2： 函数\(f(x)\)在区间\((-1，1)\)上有增有减，即函数\(y=f'(x)\)在\((-1，1)\)上至少有一个变号零点，

当有一个变号零点时，\(f'(-1)\cdot f'(1)<0\)，解得\(a\in \varnothing\)；

当有两个变号零点时，结合函数\(f'(x)=3x^2-a\)的图像的对称性可知，

转化为函数\(y=f'(x)\)在\((0，1)\)上有一个变号零点，故\(f'(0)\cdot f'(1)<0\)，

解得\(0<a<3\)。

综上可知，\(0<a<3\)。

题组案例3

已知集合 \(A=\{x\mid x^2-3x+2=0, x\in R\}\)， \(B=\{x\mid 0<x<6, x\in N\}\)，则满足条件 \(A\subseteq M\subseteq B\)的集合\(M\)有几个？

分析：由题意可知，集合 \(A=\{1，2\}\)，集合 \(B=\{1，2，3，4，5\}\)，又由于 \(A\subseteq M\subseteq B\)，

则集合\(M\)的元素最少有两个，应该是用元素\(1\)，\(2\)保底，在此基础上，再从\(3\)，\(4\)，\(5\)三个元素中选取部分元素添加进去即可，

添加的元素最少应该是\(0\)个，最多是三个，故本题目等价于集合\(\{3，4，5\}\)的所有子集的个数\(C_3^0\)\(+\)\(C_3^1\)\(+\)\(C_3^2\)\(+\)\(C_3^3\)，故应该是\(2^3=8\)个；

为便于理解，列举如下：\(\{1，2\}\)、\(\{1，2，3\}\)、\(\{1，2，4\}\)、\(\{1，2，5\}\)、\(\{1，2，3，4\}\)、\(\{1，2，3，5\}\)、\(\{1，2，4，5\}\)、\(\{1，2，3，4，5\}\)；

解后反思：注意符号语言 \(A\subseteq M\subseteq B\) 向文字语言的转化。

题组案例4

限定条件下的均值不等式求最值；

题组案例5

正切给出方式；