转化与化归思想

前言

化归思想：根据熟知的数学结论和已知掌握的数学题目解法，把数学问题化生疏为熟练、化困难为容易、化整体为局部、化复杂为简单的解决问题的思想方法；转化思想：根据熟知的数学结论和已知掌握的数学题目解法，把数学问题化空间为平面、化高维为低维、化复杂为简单解决问题的思想方法。

使用场景

• 数形之间的相互转化，

• 未知向已知的转化，

• 模型向模型的转化

• 复数问题实数化，

• 立体问题平面化，

• 实数问题有理数化，

• 视角上的转化 比如证明\(AB\perp CD\)需要转化为\(CD\perp AB\)，以及\(V_{A-BCD}=V_{D-ABC}\)，即等体积法，等面积法。

• 维度上的转化，降维处理的素材，立体问题平面化，直线的参数方程二维坐标问题一维化，复数问题实数化，空间两点间的距离公式的推导三维到一维，二维到一维；

• 抽象问题具体化

等价转化

已知单调性求参数的取值范围；

• 已知函数\(f(x)\)在区间\((a，b)\)内单调递增，等价转化为\(f'(x)\geqslant 0\)在区间\((a，b)\)内恒成立且\(f'(x)=0\)在区间\((a，b)\)内不恒成立(即需要保证\(f(x)\)不是常函数，否则不符合题意，因为常函数没有单调性)，故求得参数的取值范围后，还需要对端点值作以验证，否则会产生错误的多余的解；而学生则容易错误转化为\(f'(x)>0\)在区间\((a，b)\)内恒成立，这样必然不包含区间的端点值，这样又会产生漏解；

存在单调性求参数的取值范围；

• 已知函数\(f(x)\)存在单调递增区间\((a，b)\)，等价转化为\(f'(x)>0\)在区间\((a，b)\)有解或者能成立；而学生则容易错误转化为\(f'(x)\ge 0\)在区间\((a，b)\)内能成立或有解，这样必然会产生错误的多余的解；

已知函数在闭区间上不单调，求参数的取值范围；

• 函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上不单调，则实数\(a\)的取值范围是_________。 \((-3，1)\)

由题可知\(f(x)\)不单调，则导函数\(y=f'(x)\)在区间\((-1，2)\)上至少有一个变号零点，而不是在区间\([-1，2]\)上至少有一个变号零点；

典例剖析

【2018福建龙岩市高三质检】若不等式\((x-a)^2+(x-lna)^2>m\)对任意\(x\in R\)，\(a\in (0，+\infty)\)恒成立，则实数\(m\)的取值范围是______________。

分析：检索自己的数学知识储备，我们能发现，不等式的左端的结构和平面内两点间的距离公式非常接近，

故我们主动联想，向两点间的距离公式的几何意义做靠拢，从而转化为求两点间的距离的最小值的平方。

解法1：表达式\((x-a)^2+(x-lna)^2\)的几何意义是直线\(y=x\)上的点\((x，x)\)到曲线\(y=lnx\)上的点\((a，lna)\)距离的平方，

如果令\(f(x)=(x-a)^2+(x-lna)^2\)，则由\(m<f(x)\)对任意\(x\in R\)，\(a\in (0，+\infty)\)恒成立，

即需要我们求\(f(x)\)的最小值；这样题目首先转化为以下的题目：

直线\(y=x\)上的动点为\(P\)，函数\(y=lnx\)上的动点是\(Q\)，求\(|PQ|\)的最小值。【等价题目】直线\(y=x\)上的点为\(P(x，x)\)，函数\(y=lnx\)上的点是\(Q(a，lna)\)，求\(\sqrt{(x-a)^2+(x-lna)^2}\)的最小值。

解：设和直线\(y=x\)平行且和函数\(y=lnx\)相切的直线为\(y=x+m\)，

切点为\(P_0(x_0，y_0)\)，则有

\(\begin{cases} y_0=x_{0}+ m \\ y_0=lnx_0 \\ f'(x_0)=\cfrac{1}{x_0}=1\end{cases}\)；

从而解得\(x_0=1，y_0=0，m=-1\)

所以所求的点点距的最小值，就转化为切点\(P_0(1，0)\)到直线\(y=x\)的点线距，或者两条直线\(y=x\)，\(y=x-1\)的线线距了。

此时\(|PQ|_{min}=\cfrac{\sqrt{2}}{2}\)；

由上述题目可知，\(f(x)_{min}=(\cfrac{\sqrt{2}}{2})^2=\cfrac{1}{2}\)，

故实数\(m\)的取值范围是\(m<\cfrac{1}{2}\)，即\(m\in (-\infty,\cfrac{1}{2})\)。

【2019届宝鸡市高三理科数学质量检测一第12题】设函数\(f(x)=(x-a)^2+(lnx^2-2a)^2\)，其中\(x>0\)，\(a\in R\)，存在\(x_0\)，使得\(f(x_0)\leq \cfrac{4}{5}\)成立，则实数\(a\)等于【\(\qquad\)】

$A.1$ $B.\cfrac{1}{5}$ $C.\cfrac{2}{5}$ $D.\cfrac{1}{2}$

分析：由于题目告诉我们，存在\(x_0\)，使得\(f(x_0)\leq \cfrac{4}{5}\)成立，

则需要我们求解函数\(f(x)\)的最小值，最容易想到的就是利用导数求解函数的最小值，

这个最小值中会含有参数\(a\)，让其小于等于\(\cfrac{4}{5}\)，求解即可。

但是观察函数的特征，你会感觉这可能不是一个很好的选择。

那么有没有更好的选择呢，详细观察所给的函数结构特征，发现其和平面内任意两点见的距离公式很接近，

所以我们可以这样考虑：

函数\(f(x)\)的最小值应该是点\((x，lnx^2)\)和点\((a，2a)\)之间的最小距离的平方，再次转化为

函数\(y=g(x)=lnx^2=2lnx\)上的动点\((x，y)\)与函数\(y=h(x)=2x\)上的动点\((m，n)\)之间的最小距离的平方，

从而问题转化为先求解曲线\(y=2lnx\)上的动点到直线\(y=2x\)的最小距离了。

利用平行线法，设直线\(y=2x+m\)与曲线相切于点\((x_0，y_0)\)，

则有\(g'(x_0)=\cfrac{2}{x_0}=2\)，解得\(x_0=1\)，

代入\(y=2lnx\)，得到\(y_0=0\)，即切点为\((1，0)\)点，

代入\(y=2x+m\)，得到\(m=-2\)

即切线为\(y=2x-2\)，此时函数\(f(x)\)的最小值，也就是曲线上的点\((1，0)\)到直线\(y=2x\)的点线距的平方，

也是两条直线\(y=2x\)和\(y=2x-2\)之间的线线距的平方，其中线线距\(d=\cfrac{|2|}{\sqrt{2^2+1^2}}=\cfrac{2}{\sqrt{5}}\)

故\(d^2=\cfrac{4}{5}\)，说明这样的\(x_0\)是存在的且唯一的，\(x_0=1\)，

那么\(a\)为多少?该如何求解呢？由于\(a\)是使得函数\(f(x)\)取得最小值的参数，

即本题目中应该是点\((1，0)\)在直线\(y=2x\)上的垂足的横坐标。

由于过点\((1，0)\)和\(y=2x\)垂直的直线为\(y-0=-\cfrac{1}{2}(x-1)\)，

联立\(\left\{\begin{array}{l}{y=2x}\\{y=-\cfrac{1}{2}(x-1)}\end{array}\right.\)，解得\(x=\cfrac{1}{5}\)，

即\(a=\cfrac{1}{5}\)，故选\(B\)。

甲、乙两人约定某天晚上\(7:00 \sim 8:00\)之间在某处会面，并约定甲早到应等乙半小时，而乙早到无需等待甲即可离去，那么两个人能会面的概率是【\(\qquad\)】

$A.\cfrac{1}{3}$ $B.\cfrac{1}{8}$ $C.\cfrac{3}{8}$ $D.\cfrac{5}{9}$

分析：如右图所示，令\(7:00\)对应0，\(8:00\)对应1，设甲乙两人到达的时刻分别为\(x，y\)，则其相当于在区间\([0，1]\)上取值一样，“约定甲早到应等乙半小时”即\(y-x\leq \cfrac{1}{2}\)，即\(x-y \ge -\cfrac{1}{2}\)，“乙早到无需等待甲即可离去”意味着\(x-y>0\)，那么两人会面应该满足条件\(-\cfrac{1}{2}\leq x-y \leq 0\)，

即右图中的阴影部分，所以所求的概率为\(P=1-\cfrac{\cfrac{1}{2}\times \cfrac{1}{2}\times \cfrac{1}{2}+\cfrac{1}{2}\times 1 \times 1}{1}=\cfrac{3}{8}\).

本题目的难点有以下三个：

①到底该是用一维来刻画还是用二维来刻画；两个刻画时刻的数轴的呈现方式，到底该平行还是垂直，还是斜交。

②关于时刻的转化，\(7:00\)对应数值\(0\)，\(8:00\)对应数值\(1\)，则\(7:00 \sim 8:00\)任一时刻的到达对应区间[0，1]的任意取值。半小时对应数字\(\cfrac{1}{2}\).

③将甲、乙两人会面的文字条件转化为数学语言，即线性不等式组。

【解后反思】①本题目通过设置两个变量\(x\)，\(y\)，将已知的文字语言转化为\(x\)，\(y\)所满足的不等式(数学语言)，进而转化为坐标平面内的点\((x，y)\)的相关约束条件，从而把时间这个长度问题转化为平面图形的二维面积问题，进而转化为面积型几何概型。

②若题目中涉及三个相互独立的变量，则需将其转化为空间几何体的体积问题加以求解。

已知点\(M\)在圆\(C：x^2+y^2-4y+3=0\)上，点\(N\)在曲线\(y=1+lnx\)上，则线段\(MN\)的长度的最小值为_______。

提示：曲线\(y=1+lnx\)的切线为\(y=x\)，则原问题转化为点\((cos\theta，2+sin\theta)\)到直线\(x-y=0\)的点线距。\(d_{min}=\sqrt{2}-1\)。

对函数式或者方程式的化简会简化思维

(2017\(\cdot\)全国卷3理科第12题)【函数的零点】已知函数\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})\)有唯一的零点，则\(a\)的值为【\(\qquad\)】

$A.-\cfrac{1}{2}$ $B.\cfrac{1}{3}$ $C.\cfrac{1}{2}$ $D.1$

解法1️⃣：分离常数法，本题目就不适宜使用此法；

由\(f(x)=0\)得到\(a(e^{x-1}+e^{-x+1})=-x^2+2x\)，分离得到\(a=\cfrac{-x^2+2x}{e^{x-1}+e^{-x+1}}=h(x)\)，

你应该能感觉到函数\(h(x)\)若要用导数分析其单调性，那会是相当的难，故分离参数的思路一般在这个题目中，就自然舍弃了。

解法2️⃣：由题目可知方程\(f(x)=0\)仅有一解，即\(a(e^{x-1}+e^{-x+1})=-x^2+2x\)仅有一解，

即函数\(y=a(e^{x-1}+e^{-x+1})\)与函数\(y=-x^2+2x\)的图像仅有一个交点。参考图像

手工怎么作图呢，函数\(y=-x^2+2x\)的图像大家应该会的，故重点说\(y=a(e^{x-1}+e^{-x+1})\)的图像。

令函数\(g(x)=y=e^x+\cfrac{1}{e^x}=e^x+e^{-x}\)，则是偶函数，\(g(0)=2\)，

当\(x\ge 0\)时，\(g'(x)=e^x-e^{-x}\)，\(g'(x)\)单调递增，

故\(g'(x)\ge g'(0)=0\)，则函数\(g(x)\)在\([0，+\infty)\)上单调递增，又由偶函数可知，在\((-\infty，0]\)上单调递减，

这样我们就做出了函数\(g(x)=e^x+\cfrac{1}{e^x}\)的图像，然后将其向右平移一个单位，得到\(y=e^{x-1}+e^{-x+1}\)的图像，

前边的系数\(a\)的作用有两个，其一控制张角大小，其二控制函数最低点的位置，

就像函数\(y=a|x|\)中的\(a\)的作用一样的，所以我们就能用手工做出函数\(y=a(e^{x-1}+e^{-x+1})\)的图像，

要使得函数\(y=a(e^{x-1}+e^{-x+1})\)与函数\(y=-x^2+2x\)的图像仅有一个交点，

就需要函数\(y=a(e^{x-1}+e^{-x+1})\)的最小值\(a(e^{1-1}+e^{-1+1})=2a\)和函数\(y=-x^2+2x\)的最大值\(-1^2+2\times1=1\)相等，

故\(2a=1\)，解得\(a=\cfrac{1}{2}\)。故选\(C\).

解法3️⃣：构造函数法+函数性质法；

函数\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})=(x-1)^2+a[e^{x-1}+e^{-(x-1)}]-1\)，

令\(t=x-1\)，则\(g(t)=f(x-1)=t^2+a(e^t+e^{-t})-1\)，

由于\(g(-t)=t^2+a(e^t+e^{-t})-1=g(t)\)，故\(g(t)\)为偶函数，

由于函数\(f(x)\)有唯一零点，则函数\(g(t)\)也有唯一零点，

又函数\(g(t)\)是偶函数，即函数\(g(t)\)与\(t\)轴仅有一个交点，则\(g(0)=0\)，

代入得到\(2a-1=0\)，即\(a=\cfrac{1}{2}\)；故选\(C\).

解法4️⃣：函数\(f(x)=0\Leftrightarrow\) \(a(e^{x-1}+e^{-(x-1)})=-x^2+2x\)

\(e^{x-1}+e^{-(x-1)}\ge 2\sqrt{e^{x-1}\cdot e^{-(x-1)}}=2\)，当且仅当\(x=1\)时取到等号；

\(-x^2+2x=-(x-1)^2+1\leq 1\)；

若\(a>0\)时，\(a(e^{x-1}+e^{-(x-1)})\ge 2a\)，

要使\(f(x)\)仅有一个零点，则必有\(2a=1\)，解得\(a=\cfrac{1}{2}\)；

若\(a<0\)，则函数\(f(x)\)的零点不唯一，

综上，\(a=\cfrac{1}{2}\)；故选\(C\).

解法5️⃣：由\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})\)，

得到\(f(2-x)=(2-x)^2-2(2-x)+a(e^{2-x-1}+e^{-(2-x)+1})=x^2-2x+a(e^{x-1}+e^{-x+1})\)，

所以\(f(2-x)=f(x)\)，故\(x=1\)是函数\(f(x)\)图像的对称轴。

由题意可知，函数\(f(x)\)有唯一的零点，

故只能是\(x=1\)，

即\(f(1)=1^2-2\times1+a(e^{1-1}+e^{-1+1})=0\)，

解得\(a=\cfrac{1}{2}\)，故选\(C\).

解法6️⃣：我们一般这样转化，由函数\(f(x)\)有唯一的零点，

得到方程\(x^2-2x=-a(e^{x-1}+e^{-x+1})\)有唯一解，注意到方程的右端，

我们可以和对勾函数做以联系，令\(x-1=t\)，则\(x=t+1\)，

故原方程就转化为\((t+1)^2-2(t+1)=-a(e^t+e^{-t})\)，为了便于做出图像，

还需要再代换，令\(e^t=x\)，则\(x>0\)且\(t=lnx\)，

这样方程就又转化为\(ln^2x-1=-a(x+\cfrac{1}{x})\)，

在同一个坐标系中，分别做出函数\(y=ln^2x-1\)和\(y=-a(x+\cfrac{1}{x})\)的图像，

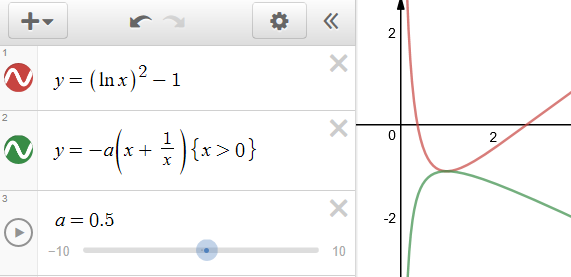
由图像可知对勾函数前面的系数必须满足\(-a=-\cfrac{1}{2}\)，即 \(a=\cfrac{1}{2}\)，故选 \(C\).

【2020届宝鸡质检1文数第12题】若过点\(P(-1,m)\)可作曲线\(f(x)=-x^3+6x^2\)的三条切线，则实数\(m\)的取值范围是【\(\qquad\)】

$A.-19< m < 8$ $B.-20 < m < 7$ $C.m < -19或m > 8$ $D.m < -20或m > 7$

法1：从形的角度分析；用导数工具分析函数\(f(x)\)的单调性，做出其简图，如图所示，

当点\(P\)在直线\(x=-1\)的下端[无穷远处]时，我们做不出过点\(P\)的三条切线，故可以排除\(C\)和\(D\)两个选项；

比较选项\(A\)和\(B\)，我们考虑\(m=7\)，此时点\(P\)位于点\(B\)处，若\(m>7\)，我们更加做不出过点\(P\)的三条切线，

故选\(B\)；

法2：从数的角度入手计算；\(f'(x)=-3x^2+12x\)，设经过点\(P\)的直线和函数\(f(x)\)相切于点\(Q(x_0，y_0)\)，

[不着急考虑有三条切线的问题，到时候写出切线方程，让其有三个解即可]

则\(\left\{\begin{array}{l}{k=f'(x_0))=-3x_0^2+12x_0①，斜率角度}\\{y_0=-x_0^3+6x_0^2②，切点在曲线上}\end{array}\right.\)

又由于切线方程为\(y-y_0=f'(x_0)(x-x_0)\)，将上述条件代入得到，

\(y-(-x_0^3+6x_0^2)=(-3x_0^2+12x_0)(x-x_0)\)，又由于动点\(P(-1,m)\)在切线上，则有

\(m-(-x_0^3+6x_0^2)=(-3x_0^2+12x_0)(-1-x_0)\)，整理得到，\(m=2x_0^3-3x_0^2-12x_0\)，

[此处注意，虽说上述结果只有一个表达式，其实它可以包含切线的三个位置]

因此，函数\(y=m\)和函数\(g(x)=2x^3-3x^2-12x\)的图像应该有三个不同的交点；

由于\(g'(x)=6x^2-6x-12=6(x^2-x-2)=6(x+1)(x-2)\)，

故函数\(g(x)\)在\((-\infty，-1)\)单调递增，在\((-1，2)\)单调递减，在\((2，+\infty)\)单调递增，

显然\(g(x)_{极大}=g(-1)=7\)，\(g(x)_{极小}=g(2)=-20\)，

做出两个函数的简图，如图所示，

由图可知，\(-20<m<7\)，故选\(B\)。

【抽象问题具体化】从一堆产品(正品与次品都多于\(2\)件)中任取\(2\)件，观察正品件数和次品件数，则下列说法：

①“恰好有\(1\)件次品”和“恰好\(2\)件都是次品”是互斥事件；

②“至少有\(1\)件正品”和“全是次品”是对立事件；

③“至少有\(1\)件正品”和“至少有\(1\)件次品”是互斥事件但不是对立事件；

④“至少有\(1\)件次品”和“全是正品”是互斥事件也是对立事件；

其中正确的有【① ② ④】；

分析：假设正品有\(A、B、C\)三件，次品有\(D、E、F\)三件[具体化时，数目刚满足题意即可，越少越好]，依次得到选项中的各事件；

在选项①中，“恰好有\(1\)件次品”包括\((A,D)\)，\((A,E)\)，\((A,F)\)，\((B,D)\)，\((B,E)\)，\((B,F)\)，\((C,D)\)，\((C,E)\)，\((C,F)\)共9个基本事件；“恰好\(2\)件都是次品”包括\((D,E)\)，\((D,F)\)，\((E,F)\)共3个基本事件，这两个事件是互斥事件，故①正确；

在选项②中，“至少有\(1\)件正品”包括\((A,B)\)，\((A,C)\)，\((B,C)\)、\((A,D)\)，\((A,E)\)，\((A,F)\)，\((B,D)\)，\((B,E)\)，\((B,F)\)，\((C,D)\)，\((C,E)\)，\((C,F)\)共12个基本事件；“全是次品”包括\((D,E)\)，\((D,F)\)，\((E,F)\)共3个基本事件，这两个事件的交集为空集，并集为全集[\(C_6^2=15\)]，因此是对立事件，故①正确；

在选项③中，“至少有\(1\)件正品”包括\((A,B)\)，\((A,C)\)，\((B,C)\)、\((A,D)\)，\((A,E)\)，\((A,F)\)，\((B,D)\)，\((B,E)\)，\((B,F)\)，\((C,D)\)，\((C,E)\)，\((C,F)\)共12个基本事件；“至少有\(1\)件次品”包括\((A,D)\)，\((A,E)\)，\((A,F)\)，\((B,D)\)，\((B,E)\)，\((B,F)\)，\((C,D)\)，\((C,E)\)，\((C,F)\)，\((D,E)\)，\((D,F)\)，\((E,F)\)共12个基本事件；这两个事件并不是互斥事件，故③错误；

在选项④中，“至少有\(1\)件次品”包括\((A,D)\)，\((A,E)\)，\((A,F)\)，\((B,D)\)，\((B,E)\)，\((B,F)\)，\((C,D)\)，\((C,E)\)，\((C,F)\)，\((D,E)\)，\((D,F)\)，\((E,F)\)共12个基本事件；“全是正品”包括\((A,B)\)，\((A,C)\)，\((B,C)\)共3个基本事件，这两个事件的交集为空集，并集为全集[\(C_6^2=15\)]，故④正确；

综上所述，填写① ② ④

解题策略：抽象问题具体化。

【宝鸡市二检文理科第12题】已知函数\(f(x)=a^x\)与\(g(x)=log_ax(a>0且a \neq 1)\)的图像有两个公共点，则实数\(a\)的取值范围是【\(\qquad\)】

$A.(0，e^{\frac{1}{e}})$ $B.(1，e^{\frac{2}{e}})$ $C.(1，\sqrt{e})$ $D.(1，e^{\frac{1}{e}})$

分析：先做出如右图所示的图像，从形上分析，由于函数\(f(x)=a^x\)与\(g(x)=log_ax(a>0且a \neq 1)\)互为反函数，其图像关于直线\(y=x\)对称，

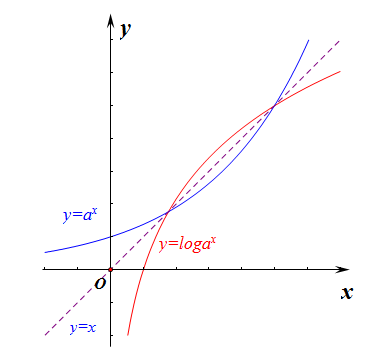
故两条曲线相交时，直线\(y=x\)必然也会过他们的交点，这样我们将图形简化一下，

即要保证两条曲线有两个交点，只需要一区一直两条线有两个交点就可以了，

此时我们从形上已经不好把握了，需要转换到数的角度进行计算。

即函数\(y=a^x\)与函数\(y=x\)的图像有两个交点，也即方程\(a^x=x\)要有两个不同的实数根。

两边同时取自然对数，得到\(lna^x=lnx\)，即\(xlna=lnx\)，注意到图像的交点的\(x\neq 0\)，

故分离参数得到\(lna=\cfrac{lnx}{x}\)，

则要方程使\(lna=\cfrac{lnx}{x}\)有两个不同的根，需要函数\(y=lna\)和\(g(x)=\cfrac{lnx}{x}\)要有两个交点，这样又转换到形了。

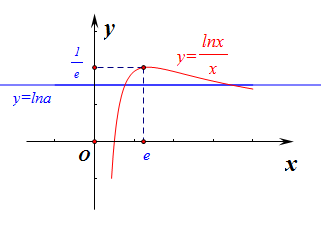
以下用导数方法，判断函数\(g(x)=\cfrac{lnx}{x}\)的单调性，得到在\((0，e)\)上单调递增，在\((e，+\infty)\)上单调递减，做出其函数图像如右图所示，

故有\(0<lna<\cfrac{1}{e}\)，即\(ln1<lna<lne^{\frac{1}{e}}\)，故\(a\in (1，e^{\frac{1}{e}})\)，选\(D\).

解后反思：①.数到形，形到数，二者之间的转换在高三数学的学习中非常普遍。②.熟练掌握函数\(f(x)=\cfrac{lnx}{x}\)，以及\(g(x)=lnx\pm x\)，\(h(x)=x\cdot lnx\)等的函数的图像和性质，在解题中会有不小的惊喜。③.在分离常数时，可以分离得出\(lna=\cfrac{lnx}{x}\)，还可以分离得到\(a=e^{\frac{lnx}{x}}\)，但是明显第一种分离方式更有利于计算，此处使用了整体思想。

大小转化

据气象部门预报，在距离某码头正西方向\(400km\)处的热带风暴中心正以\(20km/h\)的速度向东北方向移动，距离风暴中心\(300km\)以内的地区为危险区，该码头处于危险区内的时间是_____小时。

[法1]：解三角形法，设风暴移动的时间为\(t\)小时， 半径为\(300km\)的\(\odot B\)代表风暴以及殃及的范围；

则要使得码头不处于危险内，则需要\(AB>300\)；若\(AB\leqslant 300\)，则此刻码头一定在危险区内；

由题可知，\(AB^2=OA^2+OB^2-2\times OA\times OB\times cos45^{\circ}\)

即\(AB^2=400^2+400t^2-2\times20t\times400\times\cfrac{\sqrt{2}}{2}\)，

令\(AB^2\leqslant 300^2\)，即\(400^2+400t^2-2\times20t\times400\times\cfrac{\sqrt{2}}{2}\leqslant 300^2\)，

整理得到，\(400t^2-2\times20t\times400\times\cfrac{\sqrt{2}}{2}+400^2-300^2\leqslant 0\)

先变形为\(400t^2-2\times20t\times400\times\cfrac{\sqrt{2}}{2}+(400+300)(400-300)\leqslant 0\)

再变形为\(4t^2-2\times20t\times4\times\cfrac{\sqrt{2}}{2}+700\leqslant 0\)

再变形为\(t^2-2\times20t\times\cfrac{\sqrt{2}}{2}+175\leqslant 0\)

即\(t^2-20\sqrt{2}t+175\leqslant 0\)，接下来不应该考虑十字相乘法分解，应该考虑公式法。

对方程\(t^2-20\sqrt{2}t+175=0\)而言，其求根公式为

\(t=\cfrac{20\sqrt{2}\pm\sqrt{(20\sqrt{2})^2-4\times 175}}{2\times1}=\cfrac{20\sqrt{2}\pm 10}{2}=10\sqrt{2}\pm 5\)

解得\(10\sqrt{2}-5\leqslant t \leqslant 10\sqrt{2}+5\)

即当时间\(t=10\sqrt{2}-5\)时开始，码头进入危险区，当\(t=10\sqrt{2}+5\)时开始，码头脱离危险区，

所以码头处于危险区的时间为\(10\sqrt{2}+5-(10\sqrt{2}-5)=10\).

解后反思：本题目的难点比较多，①转化为解三角形模型；②对\(AB^2 \leqslant 300^2\)的理解；③解不等式，十字相乘法变换为公式法；④对\(t=10\sqrt{2}\pm 5\)的理解；

[法2]：平面几何法，将风暴理解为一个质点，将码头扩大为一个半径为\(300km\)的圆\(\odot A\)，

则当风暴沿着射线\(OD\)运动时，码头处于危险区的距离为图中的线段\(CD\)，

在\(Rt\triangle OAE\)中，容易知道\(AE=200\sqrt{2}\)，

则由相交弦定理可知，\(DE^2=(300-200\sqrt{2})\times (300+200\sqrt{2})=100^2\)，

故\(DE=100\)，\(CD=200\)，可知风暴作用于码头的距离是\(200km\)，

故码头处于危险区的时间为\(\cfrac{200}{20}=10\)小时。

动静转化

如果满足\(\angle ABC=60^{\circ}\)，\(AC=12\)，\(BC=k\)的三角形\(\Delta ABC\)恰有一个，那么\(k\)的范围是多少？

解法1️⃣：从数的角度入手，由正弦定理\(\cfrac{k}{sinA}=\cfrac{12}{sin60^{\circ}}\)，

得到方程\(k=8\sqrt{3}sinA，A\in(0，\cfrac{2\pi}{3})\)有一个解，或者两个函数图像有一个交点，数形结合求解即可。

由图可知，满足题意的三角形恰有一个，则\(k\in(0，12]\)或\(k=8\sqrt{3}\)。

解法2️⃣：从形的角度入手，动静元素互相换位，即理解为让长度为\(12\)的边变化，让长度为\(k\)的边不变化。

如图，以点\(C\)为圆心画弧，当\(12\)小于点\(C\)到边\(AB\)的高度\(k\times\cfrac{\sqrt{3}}{2}\)时，

即\(k\times\cfrac{\sqrt{3}}{2}>12\)时，解得\(k>8\sqrt{3}\)，此时三角形是不存在的；

当\(12\)等于点\(C\)到边\(AB\)的高度\(k\times\cfrac{\sqrt{3}}{2}\)时，

即\(12=k\cfrac{\sqrt{3}}{2}\)，解得\(k=8\sqrt{3}\)，三角形是唯一的；

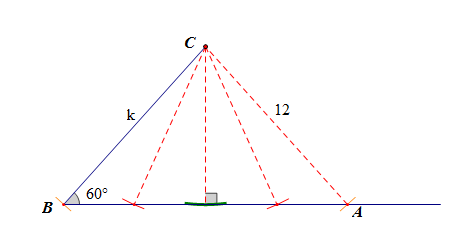
当\(12\)大于点\(C\)到边\(AB\)的高度\(k\cdot\cfrac{\sqrt{3}}{2}\)时，三角形是两个的，

即\(12>k\times \cfrac{\sqrt{3}}{2}\)，解得\(k<8\sqrt{3}\)；

当\(12\)大于或等于边\(BC\)时，三角形是唯一的，即\(0<k\leqslant 12\)，

综上可知，当\(k=8\sqrt{3}\)或\(k\in(0，12]\)时，满足条件的三角形恰好只有一个。

【解后反思】①动静互换，体现了思维的灵活性；②是否可以这样想，有一种从形入手分析的思路，必然就会有一种从数入手的思路与之对应。

图形转化

【2015\(\cdot\)全国卷Ⅰ】在平面四边形\(ABCD\)中，\(\angle A=\angle B=\angle C=75^{\circ}\)，\(BC=2\)，则\(AB\)的取值范围是___________。

分析：本题目非常特别，依据题意我们做出的图形是平面四边形，

当我们将边\(AD\)平行移动时，题目的已知条件都没有改变，故想到将此静态图变化为动态图，

平行移动\(AD\)时，我们看到了两个临界位置，即四边形变化为三角形的两个状态，

其一是四边形变化为三角形\(ABF\)，此时应该有\(BF<AB\)；

其二是四边形变化为三角形\(ABE\)，此时应该有\(BE>AB\)；

故动态的边\(AB\)的范围是\(BF<AB<BE\)，从而求解。

解答：如图所示，延长\(BA\)与\(CD\)交于\(E\)，过\(C\)做\(CF//AD\)交\(AB\)于\(F\)，则\(BF<AB<BE\)；

在等腰三角形\(CFB\)中，\(\angle FCB=30^{\circ}\)，\(CF=BC=2\)，由余弦定理得到\(BF=\sqrt{6}-\sqrt{2}\)；

在等腰三角形\(ECB\)中，\(\angle CEB=30^{\circ}\)，\(\angle ECB=75^{\circ}\)，\(BE=CE，BC=2\)，

由正弦定理得到\(BE=\sqrt{6}+\sqrt{2}\)；

故\(\sqrt{6}-\sqrt{2}<AB<\sqrt{6}+\sqrt{2}\)

解后反思引申：

1、求\(CD\)的取值范围；

分析：由上述的动态图可知，\(0<CD<CE=BE=\sqrt{6}+\sqrt{2}\)；

2、求\(AD\)的取值范围；

分析：由上述的动态图可知，\(0<AD<CF=BC=2\)；

3、求四边形\(ABCD\)的周长的取值范围；

分析：四边形\(ABCD\)的周长介于\(\Delta BCF\)的周长和\(\Delta BCE\)的周长之间，

故其取值范围是\((4+\sqrt{6}-\sqrt{2}，2(\sqrt{6}+\sqrt{2})+2)\)；

4、求四边形\(ABCD\)的面积的取值范围；

分析：四边形\(ABCD\)的面积介于\(\Delta BCF\)的面积和\(\Delta BCE\)的面积之间，

\(S_{\Delta BCF}=\cfrac{1}{2}\times 2\times 2\times sin30^{\circ}=1\)；

\(S_{\Delta BCE}=\cfrac{1}{2}\times (\sqrt{6}+\sqrt{2})\times (\sqrt{6}+\sqrt{2})\times sin30^{\circ}=2+\sqrt{3}\)；

故其取值范围是\((1，2+\sqrt{3})\)；

数形转化

【数向形的转化】【2018西安八校联考第5题】已知\(O\)是坐标原点，点\(A(2，1)\)，点\(M(x，y)\)是平面区域\(\begin{cases}&y\leq x\\&x+y\leq 1\\&y\ge -1\end{cases}\)内的一个动点，则\(\overrightarrow{OA}\cdot \overrightarrow{OM}\)的最大值是多少？

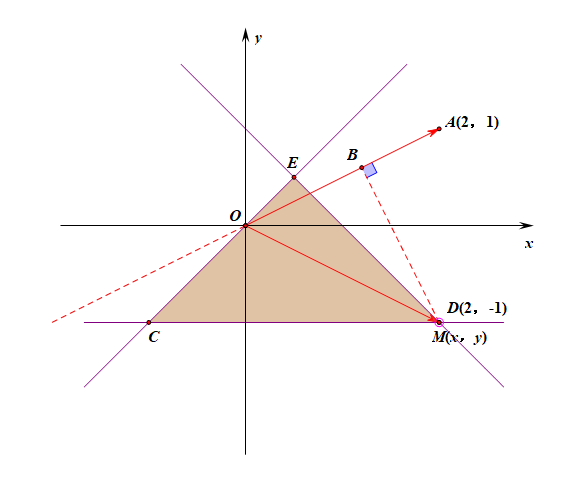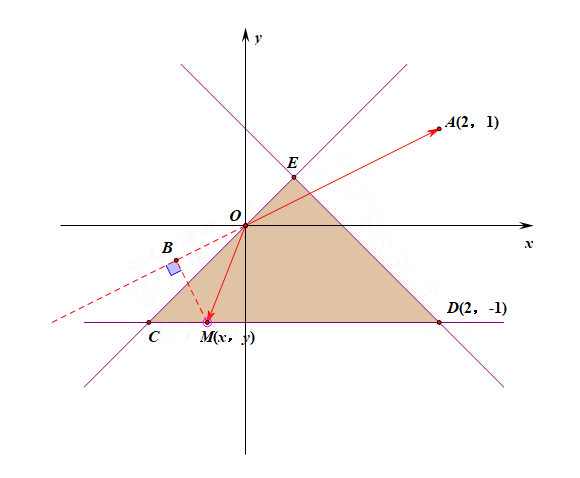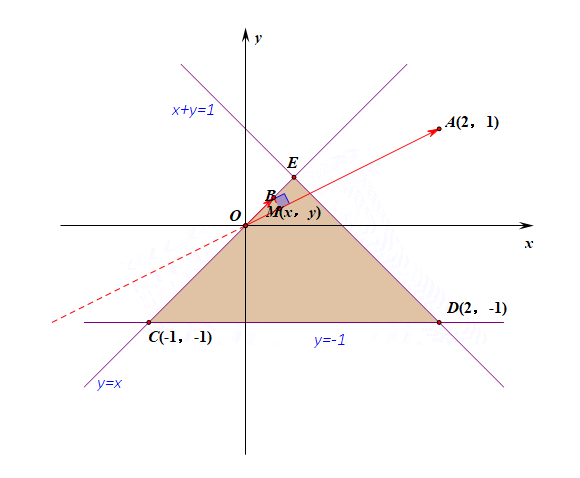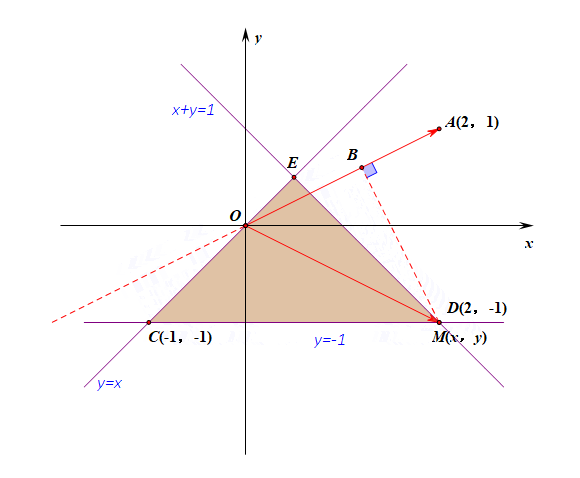
法1：利用向量的坐标运算得到，\(\overrightarrow{OA}\cdot \overrightarrow{OM}=2x+y\)，故转化为求\(2x+y\)的最大值，即求\(z=2x+y\)的最大值，用线性规划的常规方法解决即可。

法2：利用向量的投影的几何意义求解，说明：点\(M\)是三角形区域内部及边界上的一个动点，动画只做了点\(M\)在边界上的情形；

注：图中有向线段\(OB\)是向量\(\overrightarrow{OM}\)在向量\(\overrightarrow{OA}\)方向上的投影，它是可正，可负，可零的；

\(\overrightarrow{OA}\cdot \overrightarrow{OM}=|\overrightarrow{OA}|\cdot |\overrightarrow{OM}|\cdot cos\theta\)，其中\(|\overrightarrow{OA}|\)是个定值，

故只需要求\(|\overrightarrow{OM}|\cdot cos\theta\)的最大值，而\(|\overrightarrow{OM}|\cdot cos\theta\)的几何意义是\(\overrightarrow{OM}\)在\(\overrightarrow{OA}\)方向上的投影，

由图形可知，当点\(M(x，y)\)位于点\((2，-1)\)时投影\(|\overrightarrow{OM}|\cdot cos\theta\)最大，故将点\((2，-1)\)代入\(\overrightarrow{OA}\cdot \overrightarrow{OM}=3\)。

变式题1：求\(\overrightarrow{OA}\cdot \overrightarrow{OM}\)的最小值是多少？

分析：由上图可以看出，当两个向量的夹角为钝角时，其投影是负值，故当点\(M\)位于点\(C\)时，其内积最小，

此时将点\((-1，-1)\)代入得到\(\overrightarrow{OA}\cdot \overrightarrow{OM}=-3\)。

变式题2：求向量\(\overrightarrow{OM}\)的投影的绝对值最小时的动点\(M\)的轨迹方程？

分析：当其夹角为\(90^{\circ}\)时，有向线段\(OB=0\)，故向量\(\overrightarrow{OM}\)的投影的绝对值最小\(0\)；

此时，点\(M\)在三角形区域内部且和直线\(OA\)垂直，故其轨迹为\(y=-2x\),\((-1\leqslant y\leqslant 0)\)

【形向数的转化】【2025届高三数学训练题】设直线 \(x=t\) 与函数 \(f(x)\)\(=\)\(x^2\) ，函数 \(g(x)\)\(=\)\(\ln x\) 的图像分别交于点 \(M\)、\(N\)，则 \(|MN|\) 的最小值为 【\(\qquad\)】

$A.1$ $B.\cfrac{1}{4}+\ln2$ $C.\cfrac{5}{4}-\ln\cfrac{\sqrt{5}}{2}$ $D.\cfrac{1}{2}+\cfrac{1}{2}\ln 2$

分析：当我们作出如下的图形时，应该能看到用形来考虑最小值是行不通的，这涉及到两条曲线，不好思考，这时候能看到 \(M(t,t^2)\)，\(N(t,\ln t)\)，

故 \(|MN|\)\(=\)\(\sqrt{(t-t)^2+(t^2-\ln t)^2}\)\(=\)\(|t^2-\ln t|\)\(=\)\(t^2\)\(-\)\(\ln\)\(t\)，故求 \(|MN|\) 的最小值，即求函数 \(h(t)\)\(=\)\(t^2\)\(-\)\(\ln\)\(t\) 的最小值问题了 .

解：由题目可知，构造 \(h(x)\)\(=\)\(f(x)\)\(-\)\(g(x)\)\(=\)\(x^2\)\(-\)\(\ln\)\(x\)，\(x\)\(>\)\(0\)，

则 \(h'(x)\)\(=\)\(2x\)\(-\)\(\cfrac{1}{x}\)\(=\)\(\cfrac{2x^2-1}{x}\)，令 \(h'(x)\)\(=\)\(0\)，解得 \(x\)\(=\)\(\cfrac{\sqrt{2}}{2}\)，此处舍去负值，

即 \(x\)\(=\)\(\cfrac{\sqrt{2}}{2}\) 是函数的极小值点，也是最小值点，代入得到 \(h(\cfrac{\sqrt{2}}{2})\)\(=\)\(\cfrac{1}{2}\)\(+\)\(\cfrac{1}{2}\)\(\ln\)\(2\)，故选 \(D\) .

相等不等转化

已知\(a，b\in R^{+}，a+b-ab+3=0\)，求：①、求\(ab\)的范围；②、求\(a+b\)的范围；

分析：①、求\(ab\)的范围；

由题目可知，\(-3+ab=a+b\)，又由均值不等式可知\(a+b\geqslant 2\sqrt{ab}\)，

则有\(ab-2\sqrt{ab}-3\geqslant 0\)，即\((\sqrt{ab})^2-2\sqrt{ab}-3\geqslant 0\)

分解因式得到，\((\sqrt{ab}+1)(\sqrt{ab}-3) \geqslant 0\)

解得\(\sqrt{ab}\leqslant -1\) 或 \(\sqrt{ab}\geqslant 3\)

又\(a，b\in R^{+}\)，故 \(\sqrt{ab}\geqslant 3\) (当且仅当\(a=b=3\)取到等号)

给\(\sqrt{ab}\geqslant 3\)两边同时平方，得到\(ab\geqslant 9\)，即\(ab\in [9,+\infty)\)

②、求\(a+b\)的范围；

分析：\(\because a+b+3=ab \leq (\cfrac{a+b}{2})^2，令t=a+b\)

则转化为\(t^2-4t-12 \ge 0\)，解得\(t \leq -2\)(舍去) 或 $t \ge 6 $

故 \(a+b \ge 6 (当且仅当a=b=3取到等号)\)

【评析】代数式中同时有\(a+b\)和\(ab\)型，两元\(a+b，ab\)常常转化集中为一元\(a+b\)或\(ab\)，这样就好处理多了。

进退转化