机器学习课程笔记 1.2
上一篇 -> 机器学习课程笔记 1.1。
第1讲 机器学习(Machine Learning, ML)简介
5. 对线性变换函数的分析
- 我们在学习机器学习时用的是线性模型作为例子去理解, 后续其他模型训练本质和步骤也基本如此, 但不同模型函数有自身的缺陷, 下图示意了线性模型的缺陷。
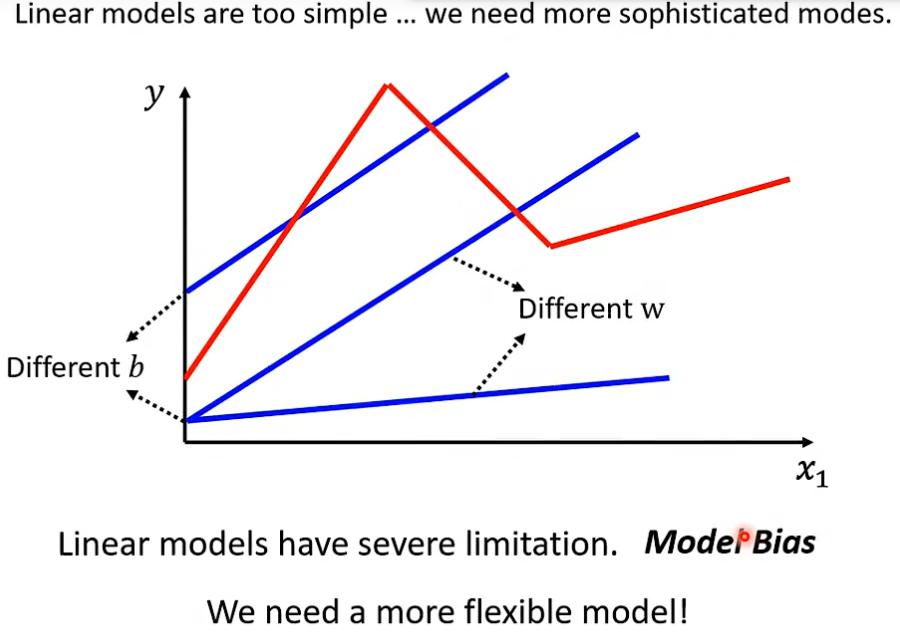
- 线性模型过于简单, 仅在有限的区域内进行变换, 所以有很多限制, 对复杂的事物规律无法很好学习参数, 也因此我们需要更复杂和灵活的模型函数。
6. 非线性函数举例
6.1 Sigmoid函数
1. 例子
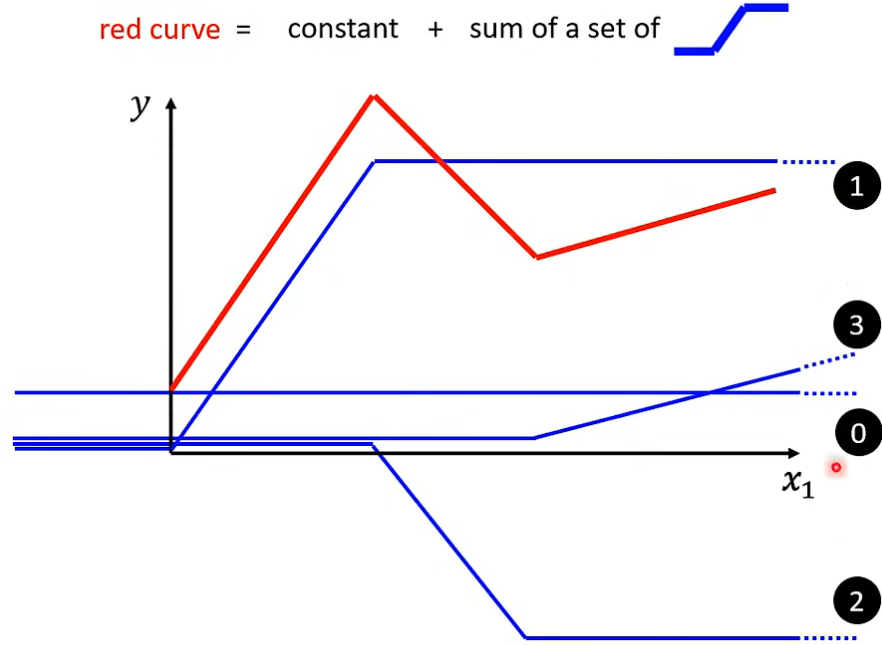
- 之前线性函数无法很好拟合的曲线, 通过 0 + 1 + 2 + 3 四条非线性曲线可以得到, 即通过 常数项 + 非线性变换函数学习到。
进一步扩展到平滑曲线, 也可以通过选点使用相同方式无限趋近原曲线。
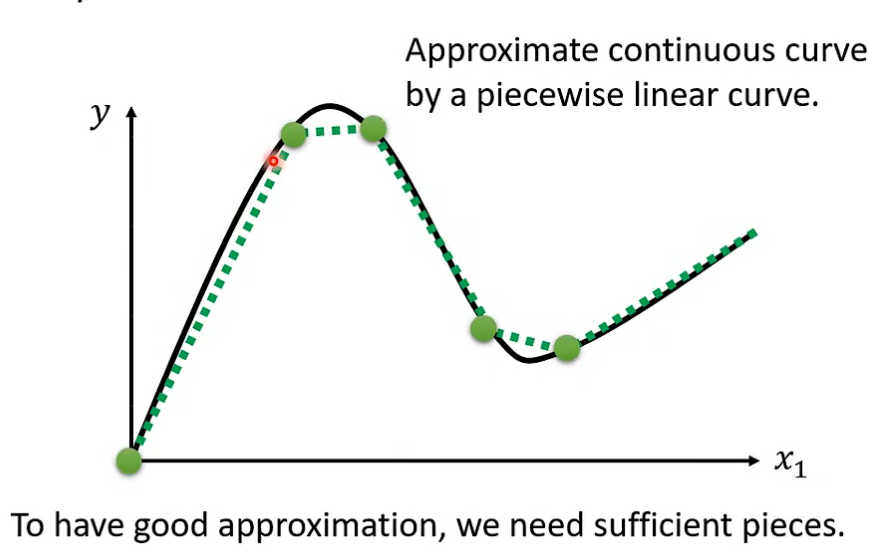
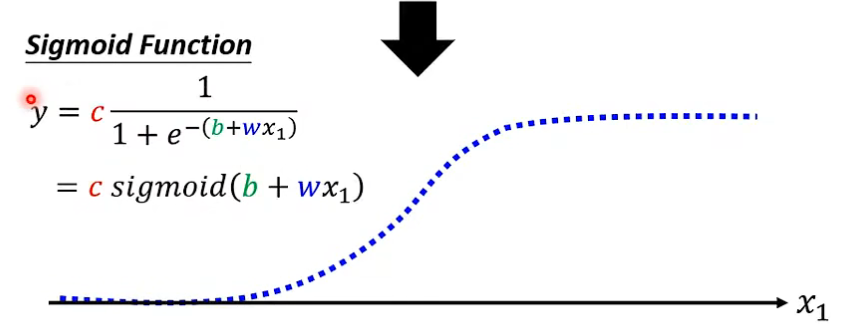
2. 给出这个非线性函数
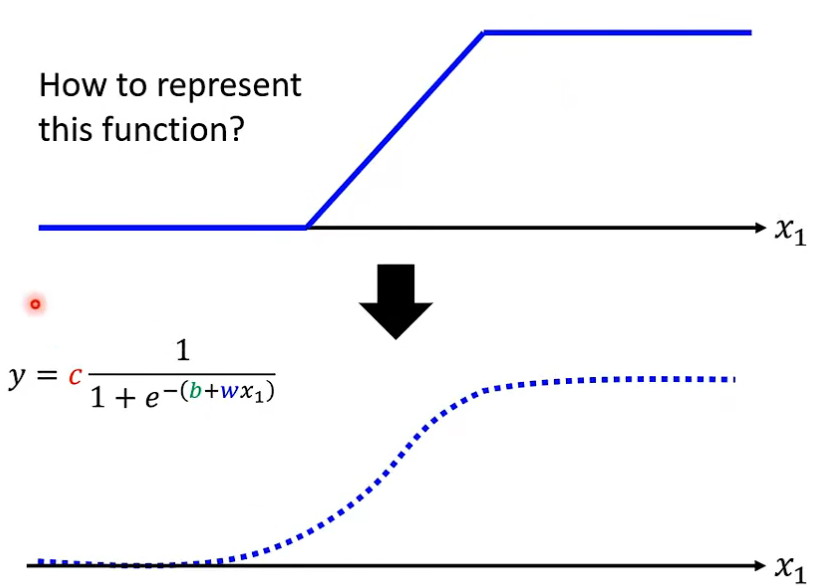
- 这条函数曲线称为 \(sigmoid\) 函数, 公式为:$$y=c\frac{1}{1+e^{-\left( b+wx_1 \right)}}$$
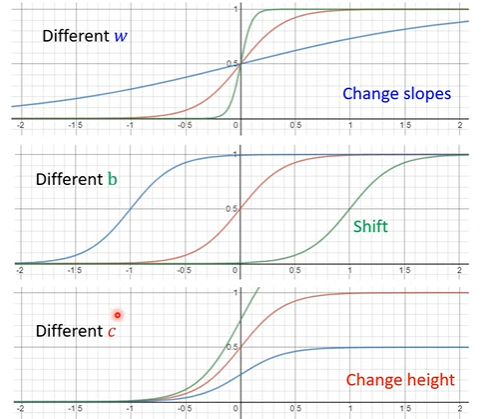
- 通过不同的参数, 可以实现不同的非线性曲线。
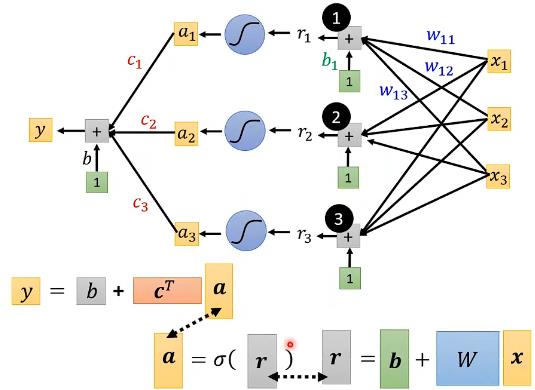
3. 计算过程
4. 损失函数
- 而除了 \(x\) 外的所有未知参数我们可以统称为 \(\theta\)。
- 则此处的损失函数可以写为 \(L(\theta)\)。
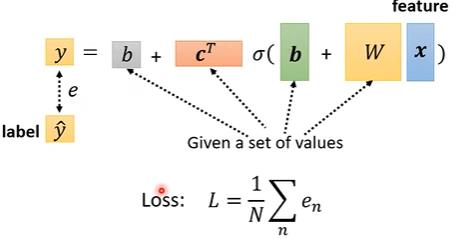
5. 参数优化
- 也是将原先的参数换为 \(\theta\), 利用优化器,如梯度下降GD等方法更新迭代未知参数, 使损失函数可以最小, 步骤如同前面线性部分所讲。
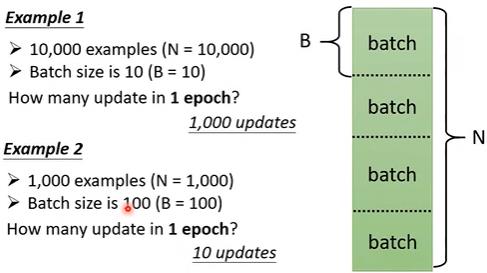
- 其次在使用GD时, 我们也可以使用批量梯度下降, 即将整个训练数据分为多个大小为 batch_size 的批次(batch)用于训练, 而所有 batch 训练一遍称为一次迭代(epoch)。其中 batch_size 和 epoch 都是人为可以设置的 超参数(hyperparameter)。
6.2 ReLU函数
1. 简介
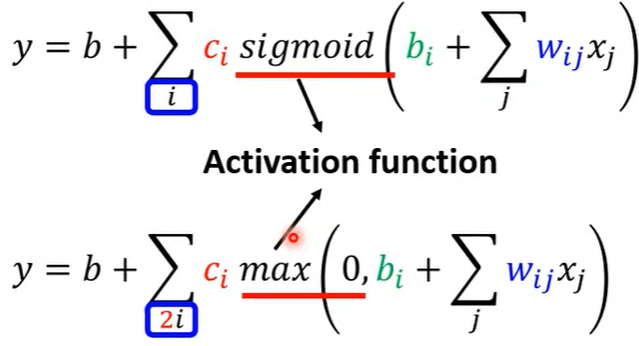
- Rectified Linear Unit(ReLU), 公式为:
\[max\left( 0,\,\,b+wx_1 \right)
\]
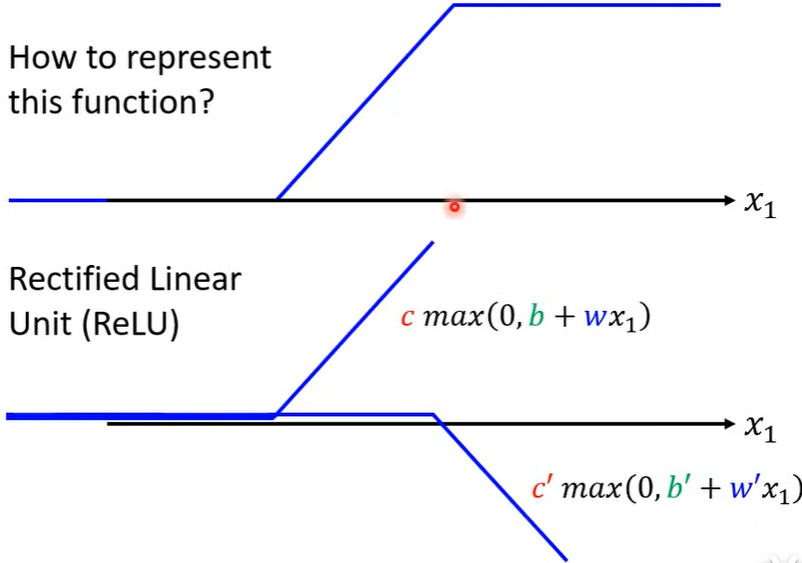
2. Sigmoid -> ReLU
- 两者都是激活函数(Activation function)。
- 两个 合适的ReLU 可以转化为 (非平滑sigmoid) Hard-Sigmoid。
3. 计算过程
4. 损失函数
- 与sigmoid时一样,只是激活函数换为 ReLU。
- 除了 \(x\) 外的所有未知参数我们可以统称为 \(\theta\)。
- 则此处的损失函数可以写为 \(L(\theta)\)。
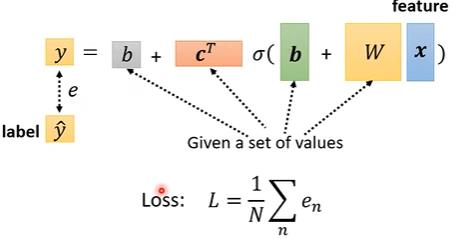
5. 参数优化
- 也是将原先的参数换为 \(\theta\), 利用优化器,如梯度下降GD等方法更新迭代未知参数, 使损失函数可以最小。
6.3 神经元 Neuron
1. 简介
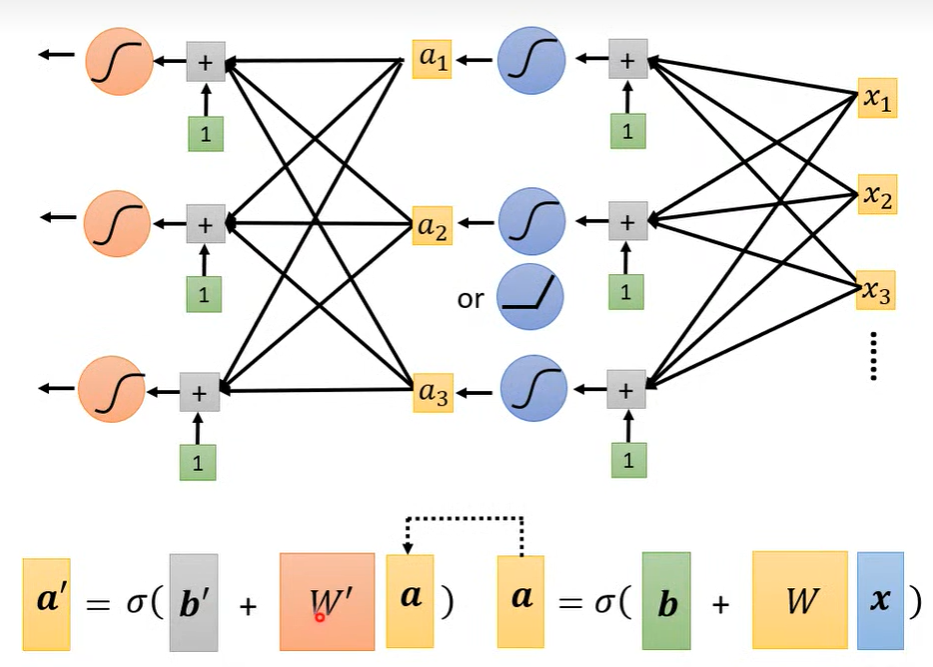
- 像sigmoid或者ReLU这样的, 每个激活函数可以看作一个神经元, 多个神经元可以构成神经网络(Neural Network)。
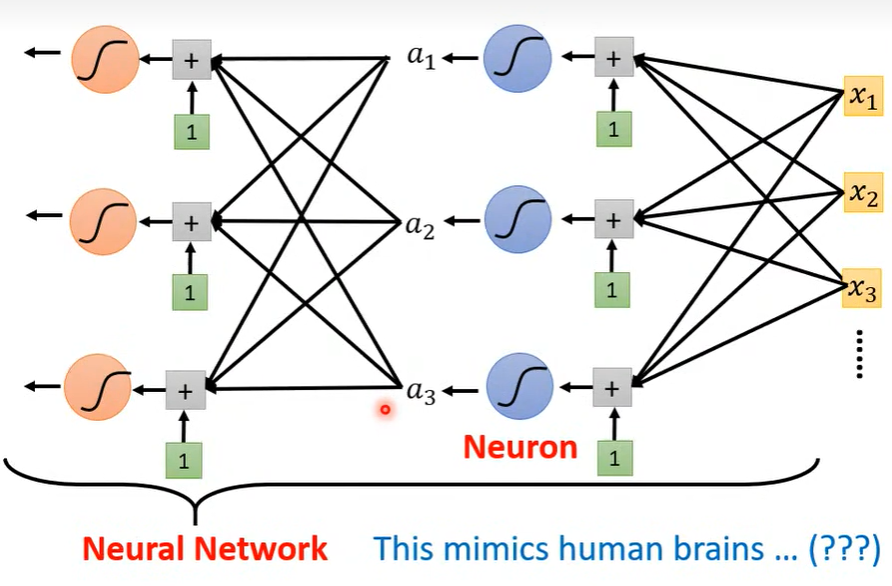
2. 深度神经网络
- 并列的一组神经元可以组成一层 隐藏层(hidden layer), 那么一直往下进行的具有多层 hidden layer 就意味着更深(Deep)。
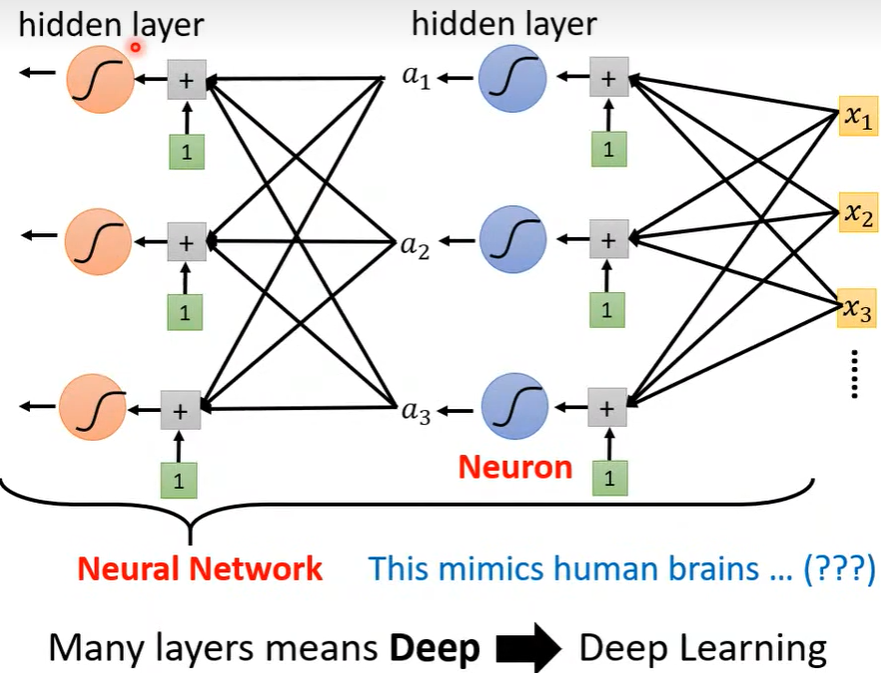
- 各种深度学习模型
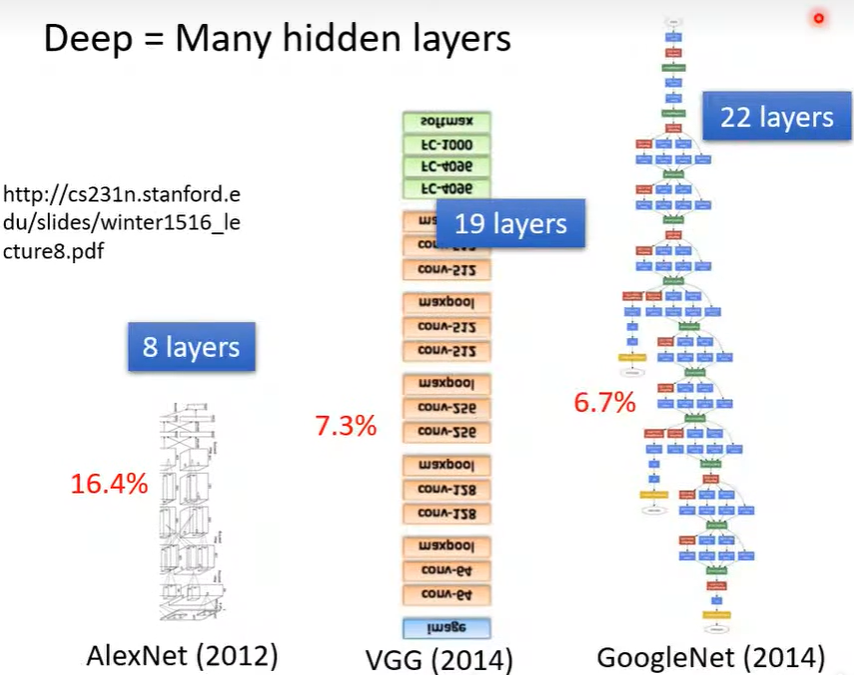

- 越深会有众多参数需要计算, 也可能会过拟合(Overfitting), 所以能这么深也需要特殊的结构才可以, 后续再说。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号