机器学习课程笔记 1.1
上一篇 -> 机器学习课程笔记 0。
第1讲 机器学习(Machine Learning, ML)简介
1. 机器学习理解
通过各种方式寻找一种函数, 可以完成事物的转换。
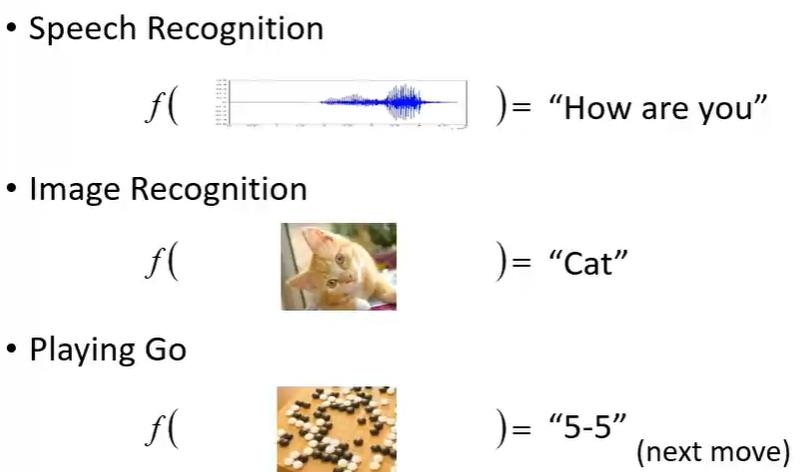
2. 不同的函数
1. 回归 Regression
- 通过历史数据, 学习参数拟合函数, 总结趋势, 预测未来数据。

2. 分类 Classification
- 通过不同类别的数据, 学习参数拟合函数, 总结类别识别方法, 做出正确分类。

- AlphaGo 也可以看出是 从 19x19 的类别中选出一个正确类别作为落子位置。
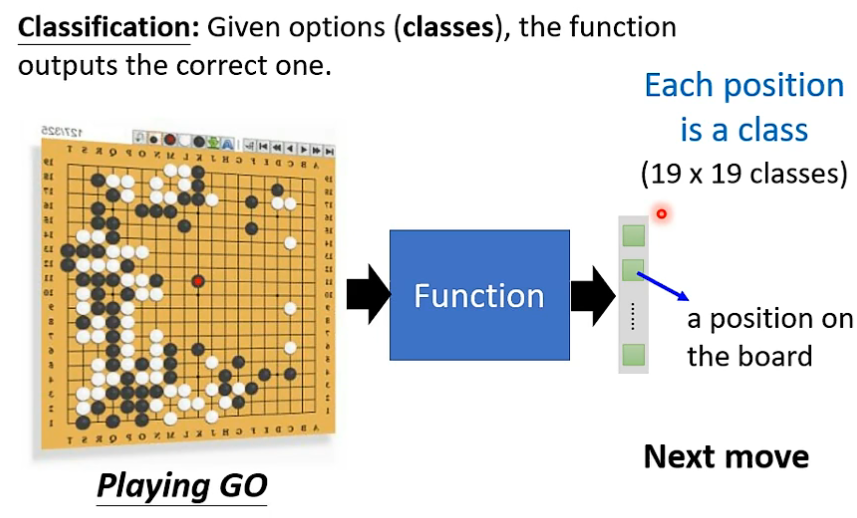
3. 其他
- 除了分类和回归, 还有一些聚类任务等。
- 这些任务, 可以被称为结构化学习任务 Structured Learning。

3. 寻找函数的方式
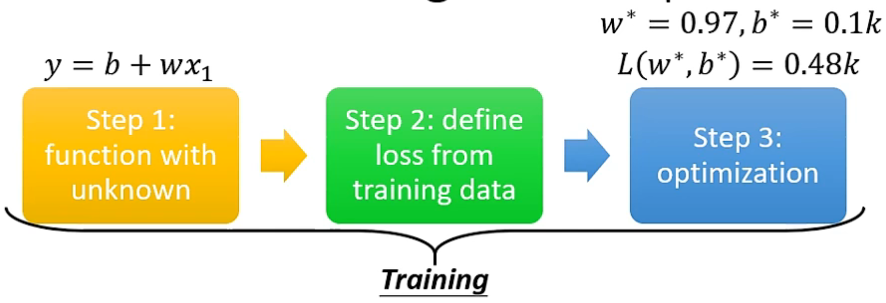
1. 步骤1 设置带有未知参数的函数
- 以通过历史视频浏览量, 预测后期视频浏览量为例子。

- 其中的 \(y = wx + b\) 就是我们所设的函数, 即模型 model, \(w\) 和 \(b\) 就是未知参数 weight 和 bias, 而 历史数据就是特征 features。
2. 步骤2 定义损失函数
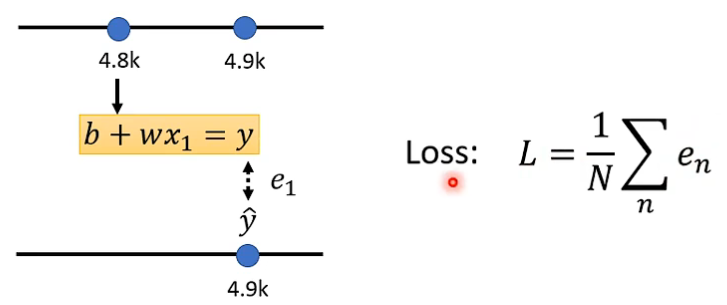
- 损失函数是衡量未知参数求得的model结果与feature的标签label之间差异 \(e\) 的相关函数, 即 \(L(b, w)\)。
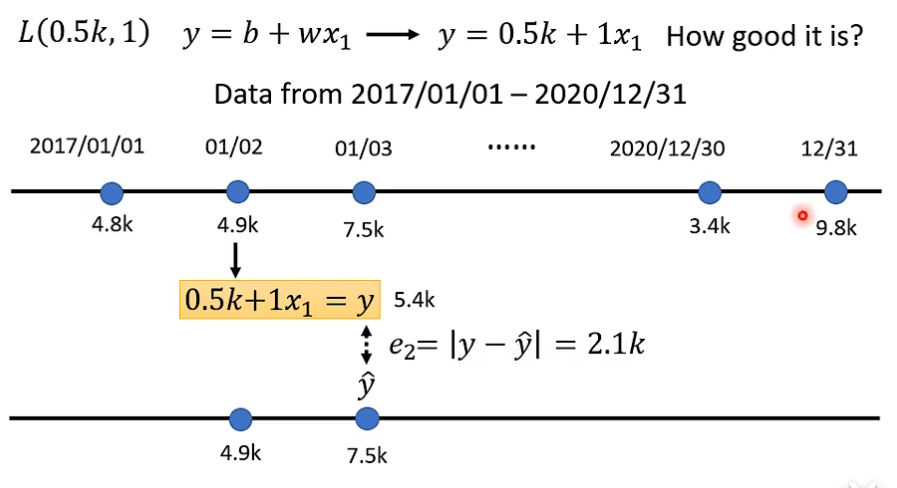
- 通过损失函数值的大小看所设置的 weight 和 bias 是否足够好。
-
每一天的 \(loss\) 加和求平均, 得到总体的 \(Loss\)。
-
计算差异常用方法有
- \(e = |y - \hat{y}|\), \(Loss\) 为 mean absolute error(MAE)。
- \(e = (y - \hat{y})^2\), \(Loss\) 为 mean square error(MSE)。
- 如果 \(y 与 \hat{y}\) 是概率分布, 会使用交叉熵 Cross-entropy。
根据调整 weight 和 bias 得出两者与 \(Loss\) 的等高线图, 越红表示差异性越大, 越蓝表示越好。
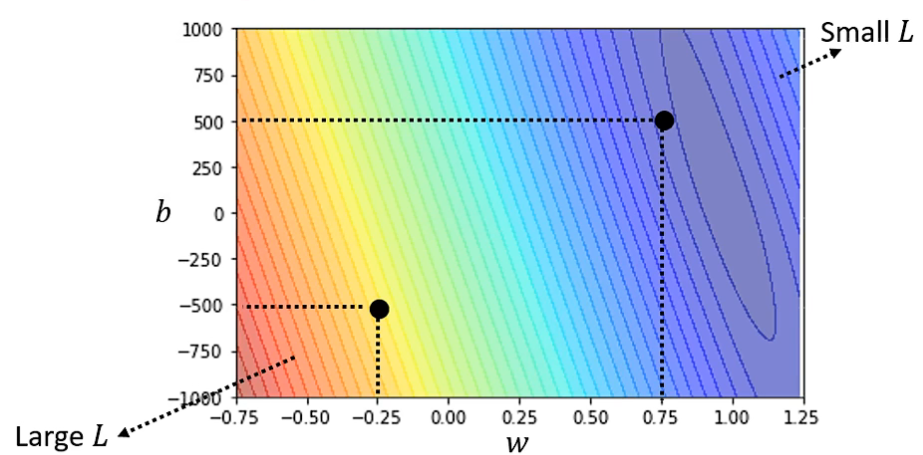
3. 步骤3 优化参数 Optimization
- 通过某种方式, 选出可以使 \(Loss\) 最小的一组 weight 和 bias, 即 \(w^*, b^* = arg\,\,\underset{w,b}{min}\,\,L\)。
- 常用方法 梯度下降 Gradient Descent:
先看一个参数 \(w\)-
首先选取一个随机的 \(w^0\)。
-
计算此时的梯度 $$\frac{\partial L}{\partial w}|_{w=w^0}$$
-
通过加负梯度更新参数大小, 即负增加, 正减小。$$w_{i+1}=w_i-\eta \cdot \frac{\partial L}{\partial w}|_{w=w^i}$$
-
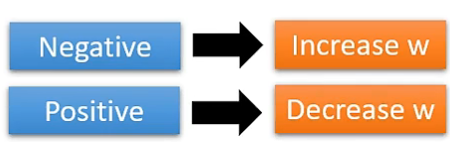
- \(\eta\) 为每次调整的幅度, 称为学习率 learning rate, 是可以手动调整的超参数 hyperparameters。

扩展到两个参数 \(w\) 和 \(b\)

4. 机器学习总结
- 通过各种方式寻找一种函数, 可以完成事物的转换。
1. 函数
- Regression 回归
- Classification 分类
- Structured Learning 结构化学习任务(聚类)
2. 寻找方式
- 步骤1 设置带有未知参数的函数
- 步骤2 定义损失函数
- 步骤3 优化参数 Optimization


 浙公网安备 33010602011771号
浙公网安备 33010602011771号