机器学习课程笔记 2

上一篇 -> 机器学习课程笔记 1.2。

第2讲 训练不如意的原因与处理

1. 局部最优解(local minima) 与 鞍点(saddle point)

• 训练到一定程度, loss 很大却不再下降 或者 一开始就 梯度很小, loss 几乎不下降。

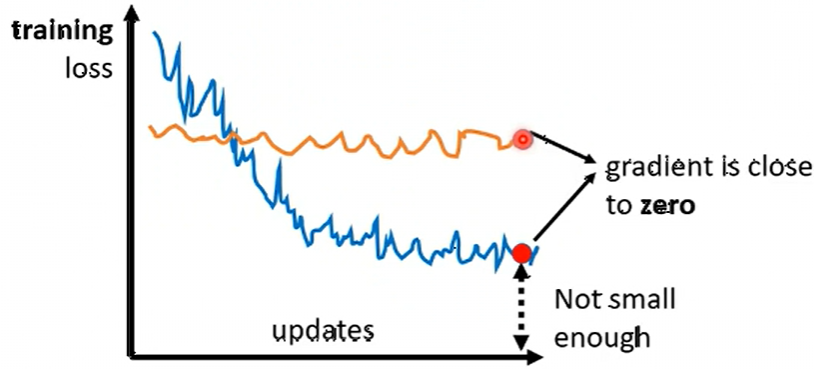
• 两种基本原因
  • 局部最优解(local minima)
    处于此时的最低点。
  • 鞍点(saddle point)
    某一方向上的最低点, 但换个方向有更小者。

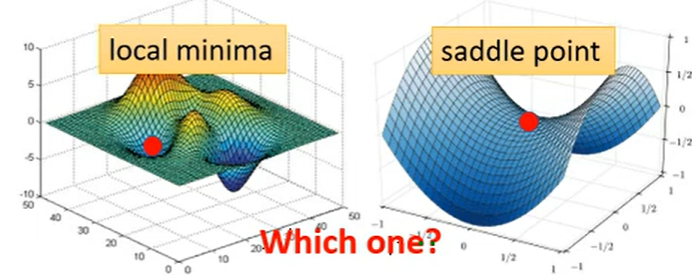
如何判断属于哪一种？

已知由泰勒公式可以满足近似关系

\[L\left( \theta \right) \approx L\left( \theta ^{\prime} \right) +\left( \theta -\theta ^{\prime} \right) g+\frac{1}{2}\left( \theta -\theta ^{\prime} \right) ^TH\left( \theta -\theta ^{\prime} \right) \]

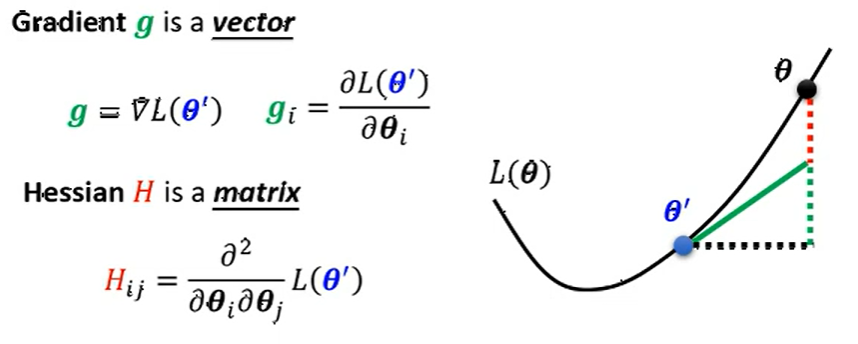
简单理解 \(g\) 是 loss 对 \(\theta^{\prime}\) 的一阶导数, \(H\) 是loss 对 \(\theta^{\prime}\) 的二阶导数, 也称为 Hessian 矩阵。而当点位于上述两种情况时, 一阶导数部分为0, 则看属于哪种情况需要比较二阶导数, 也就是 比较 Hessian 矩阵部分。

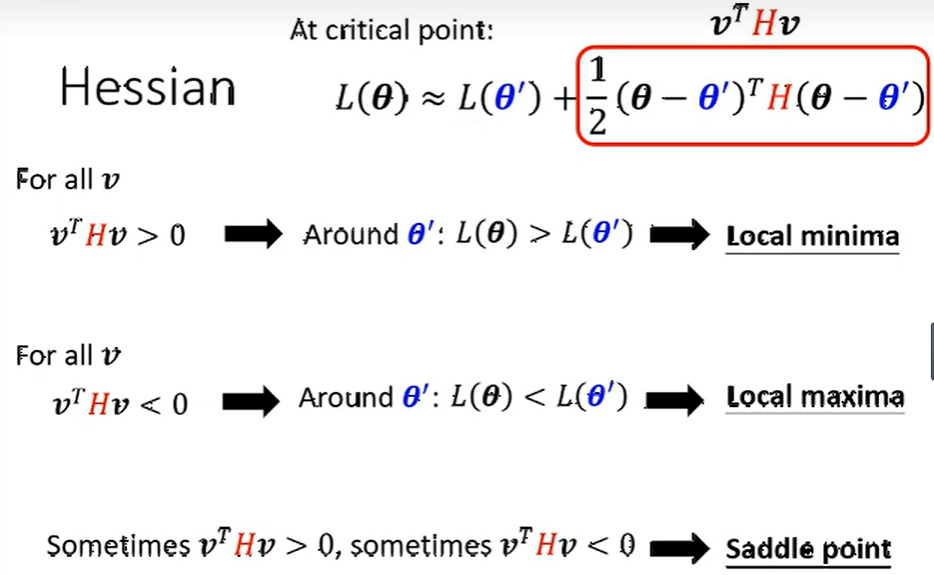
在二阶导数部分, 如果代入任何临近 \(\theta\) 结果恒小于0, 则\(\theta^{\prime}\) 处为局部最小值, 相反恒大于0为局部最大值; 而对于在0左右反复横跳的, 即为鞍点。
而二阶导数部分中, \((\theta-\theta^{\prime})\) 的平方恒大于0, 则决定结果的权利就落在了 Hessian矩阵上。所以求出其二阶导数Hessian矩阵, \(H>0\) 为局部最小值; \(H<0\) 为局部最大值; 有时\(H>0\), 有时\(H<0\) 为鞍点。

• 简单例子

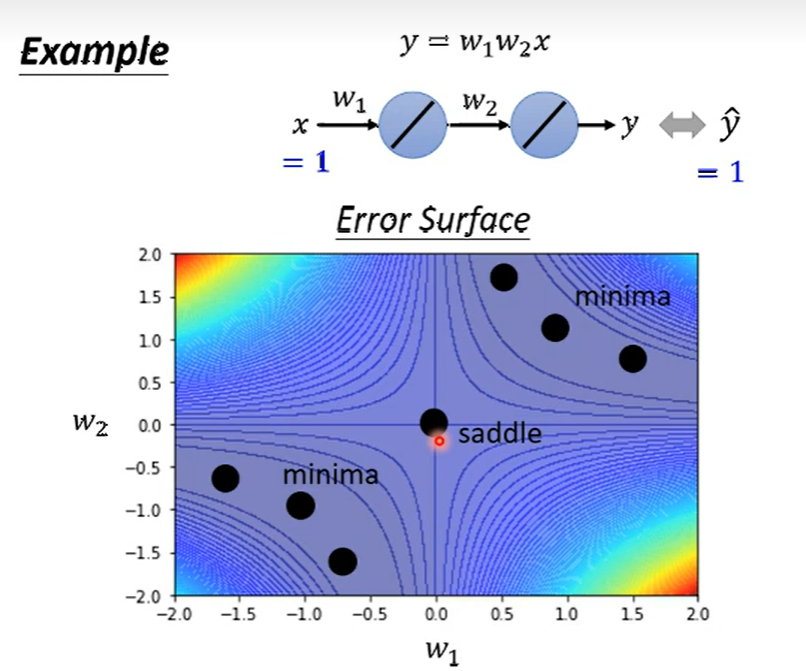
• 写出一阶导数部分, 已知 \(w_1=0, w_2=0\)。

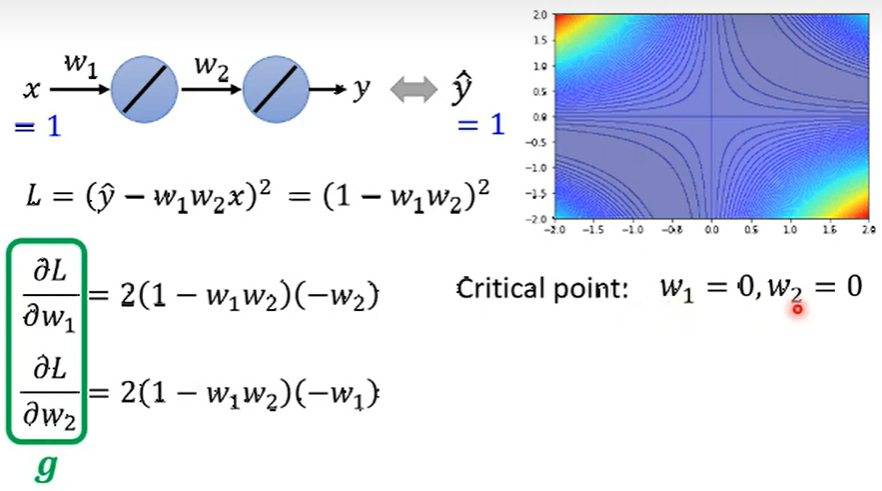
• 写出二阶导数部分, 并带入 \(w_1, w_2\)。

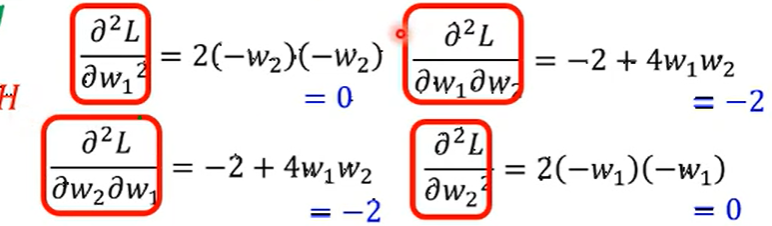
• 根据解写出 Hessian 矩阵

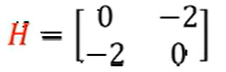
• 求解 Hessian 矩阵的特征值

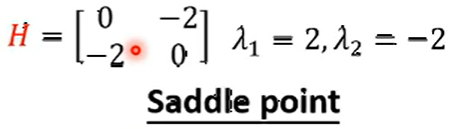
• 有正有负, 所以为鞍点。

由前面鞍点的介绍可知, 鞍点其他方向可以有更小的loss。
所以当知道为鞍点时, 可以继续按照 负特征值的特征向量的方向 继续调整参数, 来获取更小的 loss。
但现实由于 Hessian 矩阵的计算量太大, 实际不会这么应用。
而且当你有很多参数时, 局部最小值也会很稀有，很有价值。

2. 批次(batch) 与 动量(momentum)

2.1 batch

• 回顾

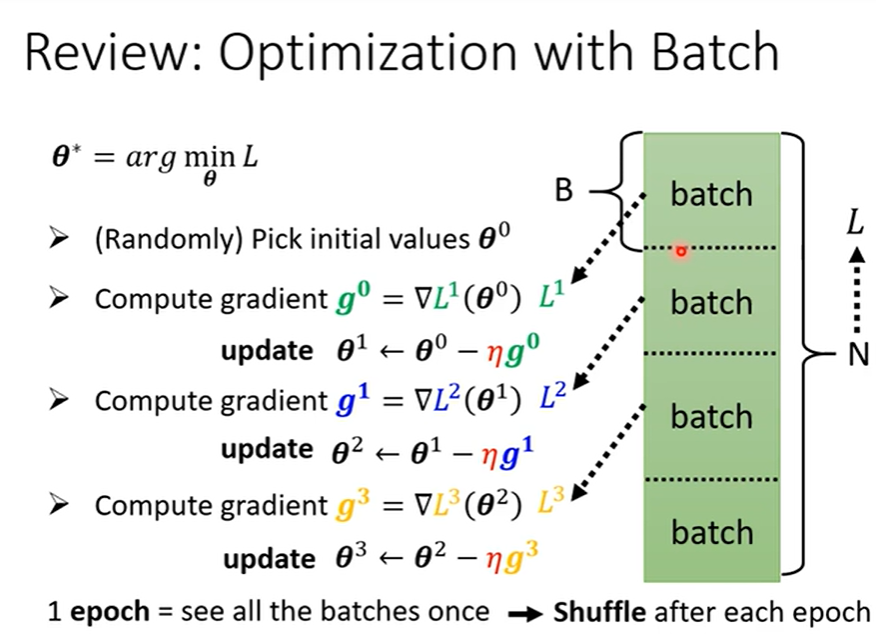
• 为何要用batch？

不用 batch 或者 bach_size = N（N 为样本总数）, 意味着将所有的样本看完, 才完成一轮更新，虽然很稳定，但当样本过大时，消耗的时间太多；而使用单例样本 或 batch = 1，意味着看一个样本算完成一次更新，虽然时间短，但每个样本的不同导致梯度下降的不稳定。

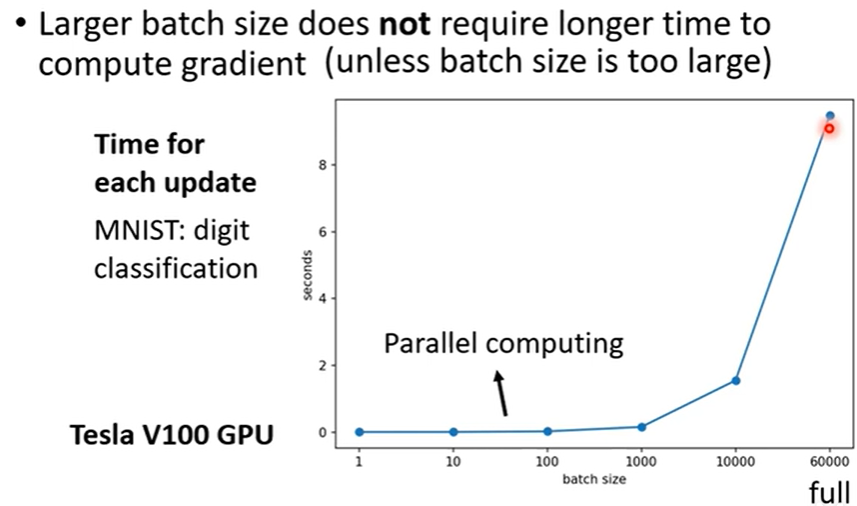
所以对大样本取适中的 batch_size 得到 batch 来训练，既可以节省时间，还能稳定下降梯度。

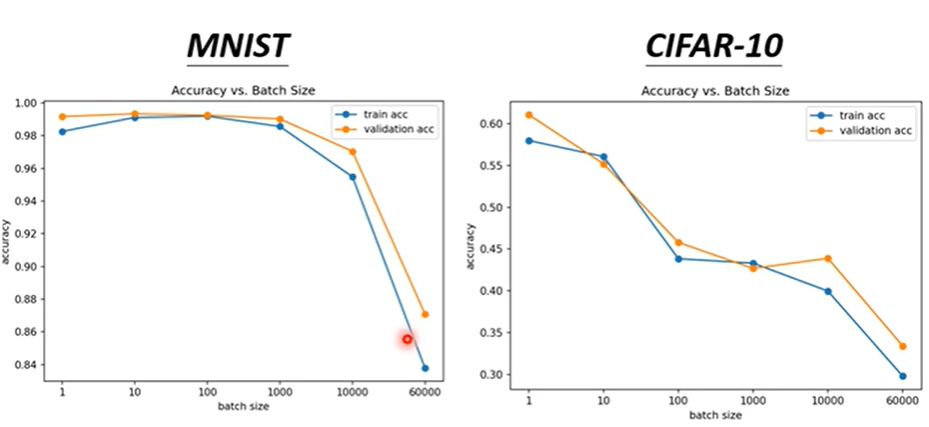
但不排除小的batch效果更好，如上图。
主要原因是优化器的选择导致。梯度更新稳定意味着进入局部最小值和鞍点出来的可能性较低，而小批量的具有波动的性质，更容易跳出其中。

所以小还是大，可以看下图比较。

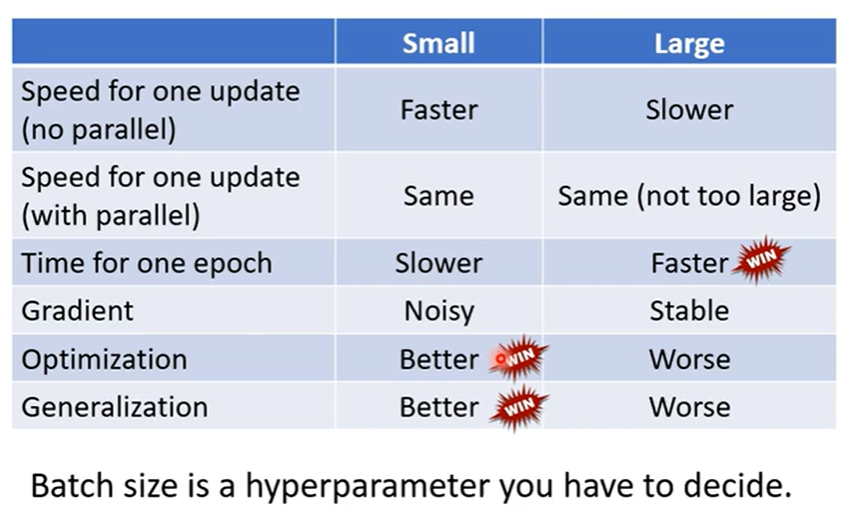
2.2 monentum 动量

• 简单来说
  为原先梯度下降的方向保留一定值，作为后续参数更新的修正。有点类似于现实世界的运动物体的惯性。

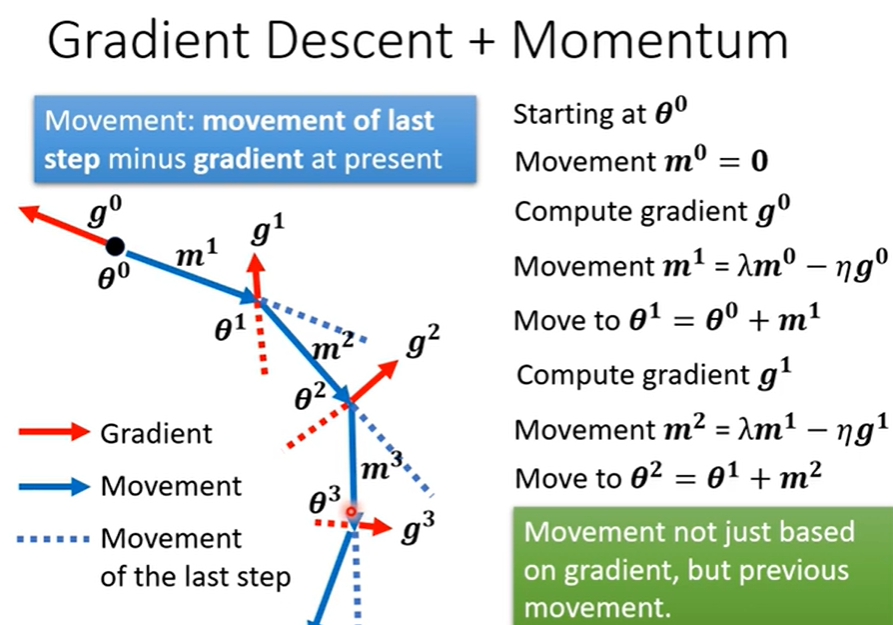
3. 自适应学习率 Adaptive Learning Rate

• 参数更新除了与梯度有关还与学习率 \(\eta\) 有关。

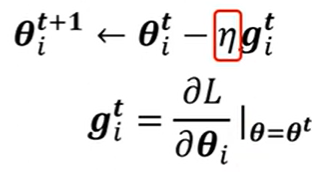
• 所以根据情况自动调整 \(\eta\) 也很重要。

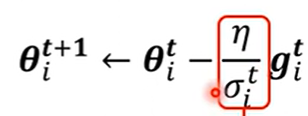
• 常见方法之 Adagrad
  \(\eta\) 除以每次梯度的均方根(Root Mean Square, RMS)
  这样的优化器也称为 Adagrad。

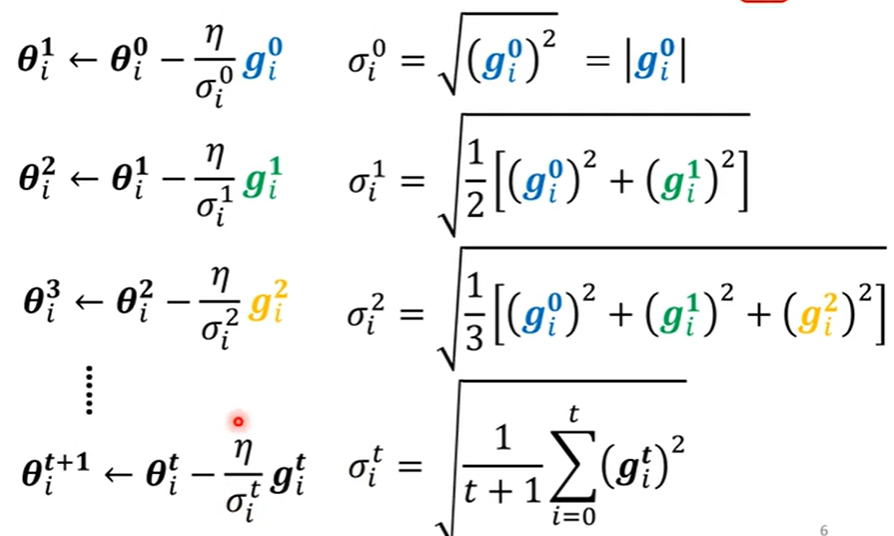
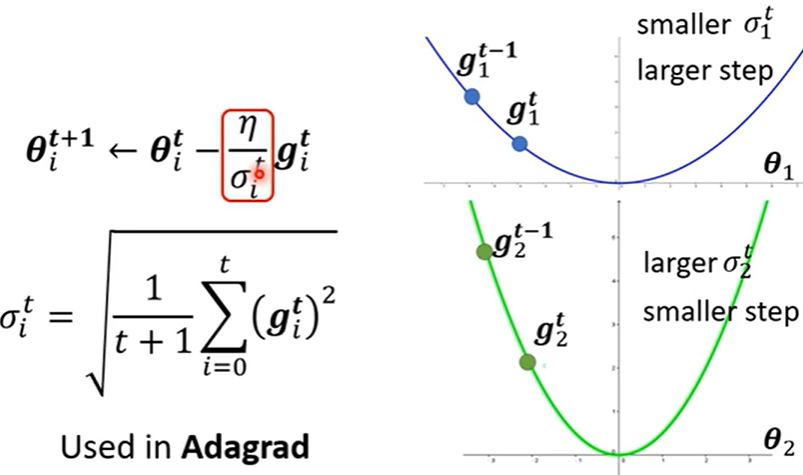
• 原理
  为了不错过最低点，当梯度很大, RMS就大，进一步 \(\eta\) 相除就会变小，更新幅度就变小；反之，更新梯度大。

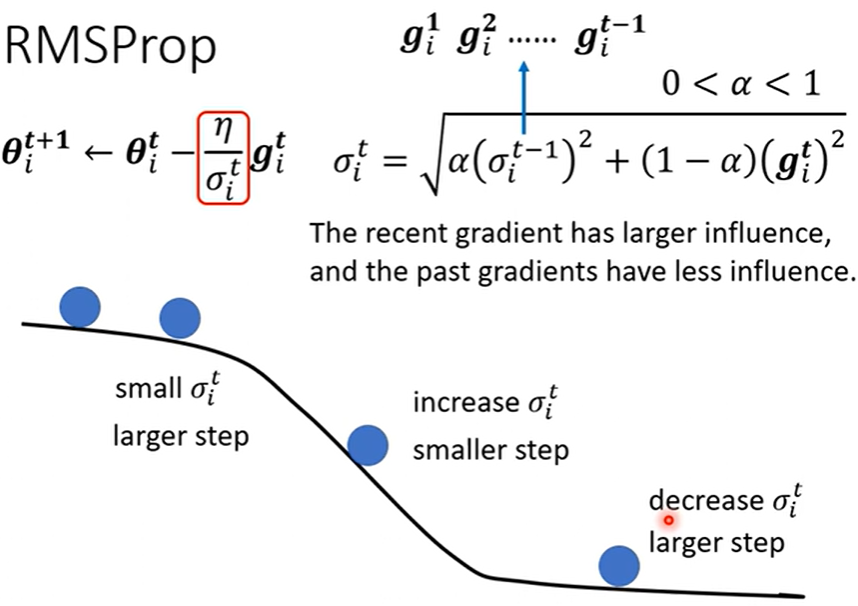
• 常见方法之 RMSProp
  Adagrad 存在一个缺点，即他的梯度是统一看待并累计的，这样每个时刻的梯度对学习率的调整是同样权重的，则不管大的小的，统一规划为均值去调，这样就导致学习率的调整过于均衡。
  所以提出了给相邻时刻梯度权重 \(\alpha\) 的 RMSProp 优化器。

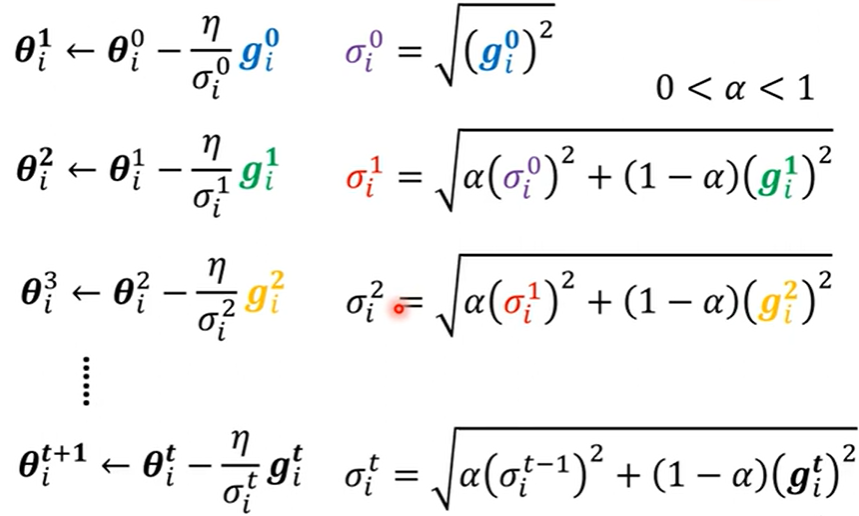
• 原理
  加入权重后，可以让近期的梯度对学习率的调整有更大的影响，进而学习率调整的更加准确。

• 现实常用 Adam
  Adam 其实就是 RMSProp + Momentum。
  即 RMSProp 部分调整学习率，Monentum 部分调整梯度。

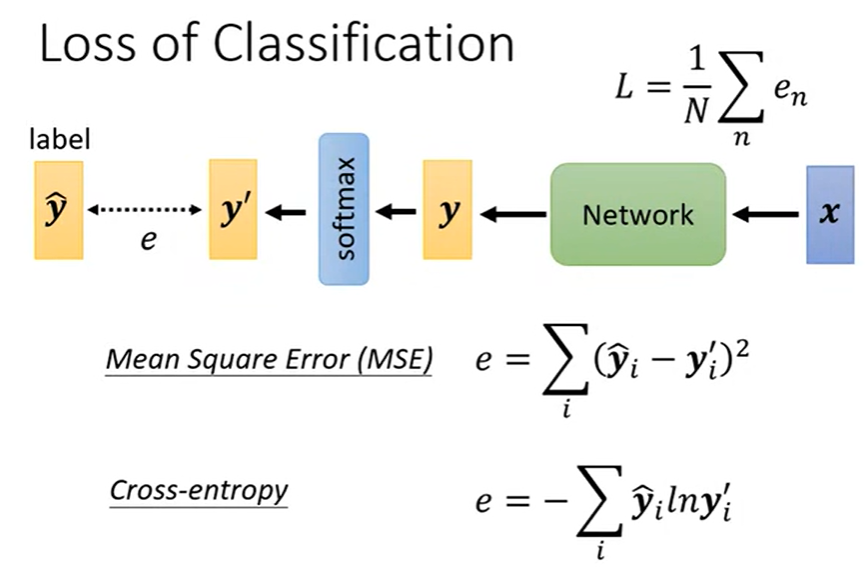
4. 损失函数 Loss

分类常用交叉函数 Cross Entropy。

下一篇 -> 机器学习课程笔记 3。