摘要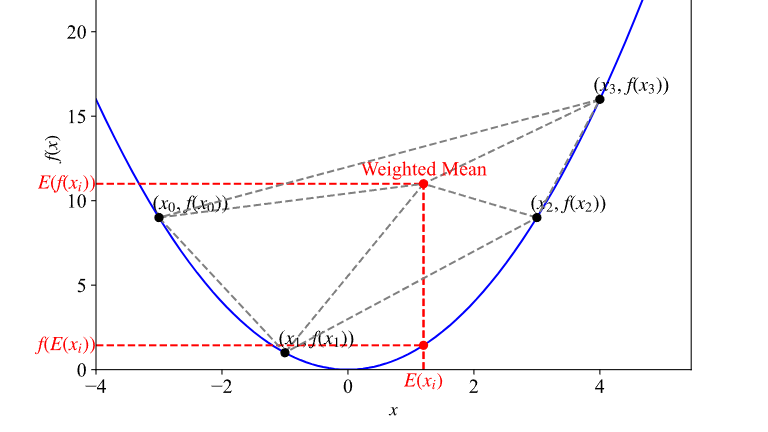：Jenson不等式描述对于一个凸函数，期望值与函数作用后的期望值之间的关系。本文对其进行可视化以获取直观理解。 对于积分为1的非负函数$p(x)$，即 $\displaystyle\int_{-\infty}^{\infty}p(x) dx = 1$ 假设$f(x)$为下凸函数，$g(x)$为任意可 阅读全文

摘要：Deep Variational Information Bottleneck (VIB) 变分信息瓶颈 论文阅读笔记。本文利用变分推断将信息瓶颈框架适应到深度学习模型中，可视为一种正则化方法。 变分信息瓶颈 假设数据输入输出对为$(X,Y)$，假设判别模型$f_\theta(\cdot)$有关于$ 阅读全文

摘要：在深度学习中，我们通常对模型进行抽样并计算与真实样本之间的损失，来估计模型分布与真实分布之间的差异。并且损失可以定义得很简单，比如二范数即可。但是对于已知参数的两个确定分布之间的差异，我们就要通过推导的方式来计算了。 下面对已知均值与协方差矩阵的两个多维高斯分布之间的KL散度进行推导。当然，因为便于 阅读全文

摘要：傅里叶（Fourier）级数是三角级数（每项都是三角函数）的一种。因为项数无限，且其中任意两个不同函数项之积在$[-\pi,\pi]$上的积分为0，所以可以作为希尔伯特空间的一个正交系。傅里叶级数可以拟合很多周期函数。 三角函数系的正交性 三角函数系 $1,\cos x,\sin x,\cos 2x 阅读全文

摘要：下面介绍的各种熵尽管都与数据分布的混乱度相关，但是建议把相对熵（KL散度）和交叉熵单独拿出来理解。交叉熵和相对熵是针对同一个随机变量，它们是机器学习里额外定义的用来评估两个分布差异的方式，无法用韦恩图进行观察；而后面的条件熵等则是针对不同的随机变量之间的关系（可以看完本文再回来看这句话）。 信息熵 阅读全文