04.神经网络
神经网络概述
人工神经网络(Artificia NeuralNetwork，简写为ANN)也简称为神经网络(NN)，是一种模仿生物神经网络结构和功能的计算模型。人脑可以看做是一个生物神经网络，由众多的神经元连接而成。各个神经元传递复杂的电信号，树突接收到输入信号，然后对信号进行处理，通过轴突输出信号。下图是生物神经元示意图:
那怎么构建人工神经网络中的神经元呢?
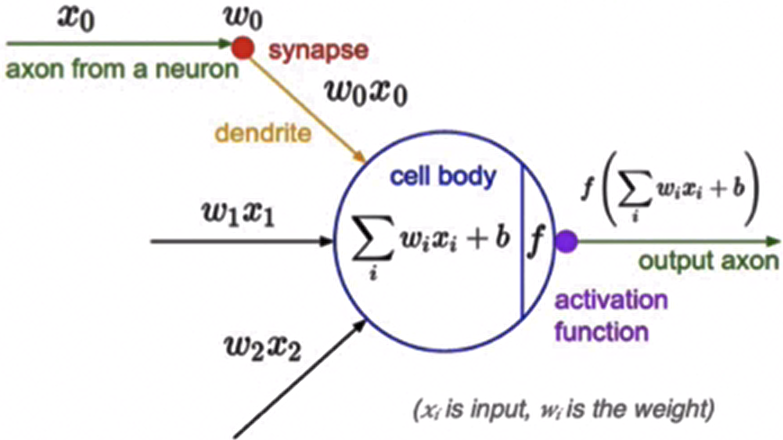
受生物神经元的启发，人工神经元接收来自其他神经元或外部源的输入，每个输入都有一个相关的权值(w)，它是根据该输入对当前神经元的重要性来确定的，对该输入加权并与其他输入求和后经过一个激活函数f，计算得到该神经元的输出。
那接下来我们就利用神经元来构建神经网络，相邻层之间的神经元相互连接，并给每一个连接分配一个强度，如下图所示:
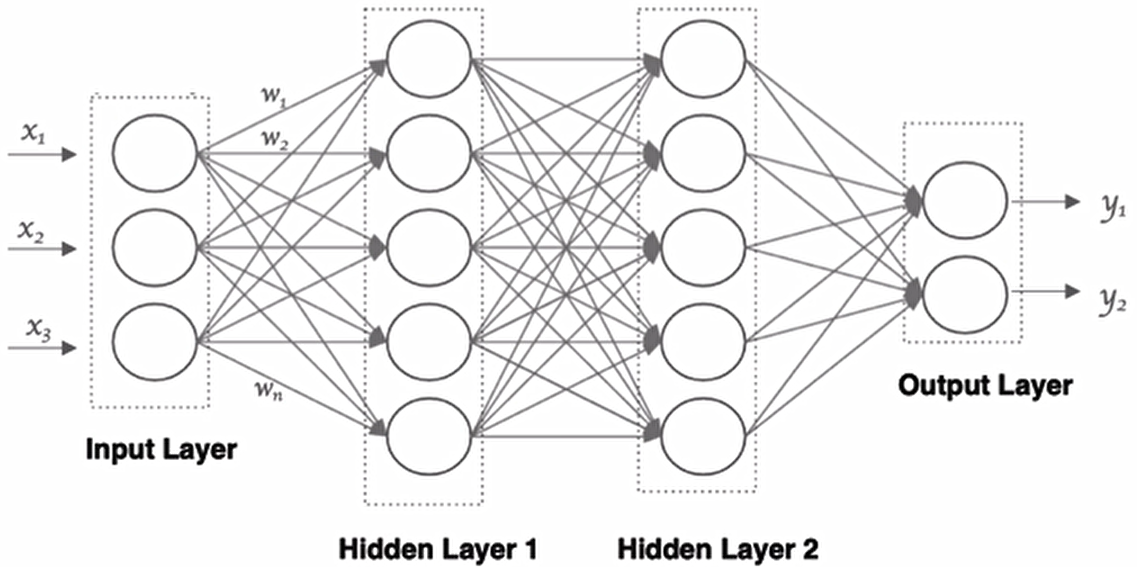
神经网络中信息只向一个方向移动，即从输入节点向前移动，通过隐藏节点，再向输出节点移动网络中没有循环或者环。其中的基本构件是:
- 输入层:即输入x的那一层
- 输出层:即输出y的那一层
- 隐藏层:输入层和输出层之间都是隐藏层
特点是：
- 同一层的神经元之间没有连接。
- 第N层的每个神经元和第N-1层的所有神经元相连(这就是ful connected的含义)，第N-1层神经元的输出就是第N层神经元的输入。
- 每个连接都有一个权值。
损失函数
优化算法
激活函数
参数初始化
神经网络的搭建
接下来我们来构建如下图所示的神经网络模型:
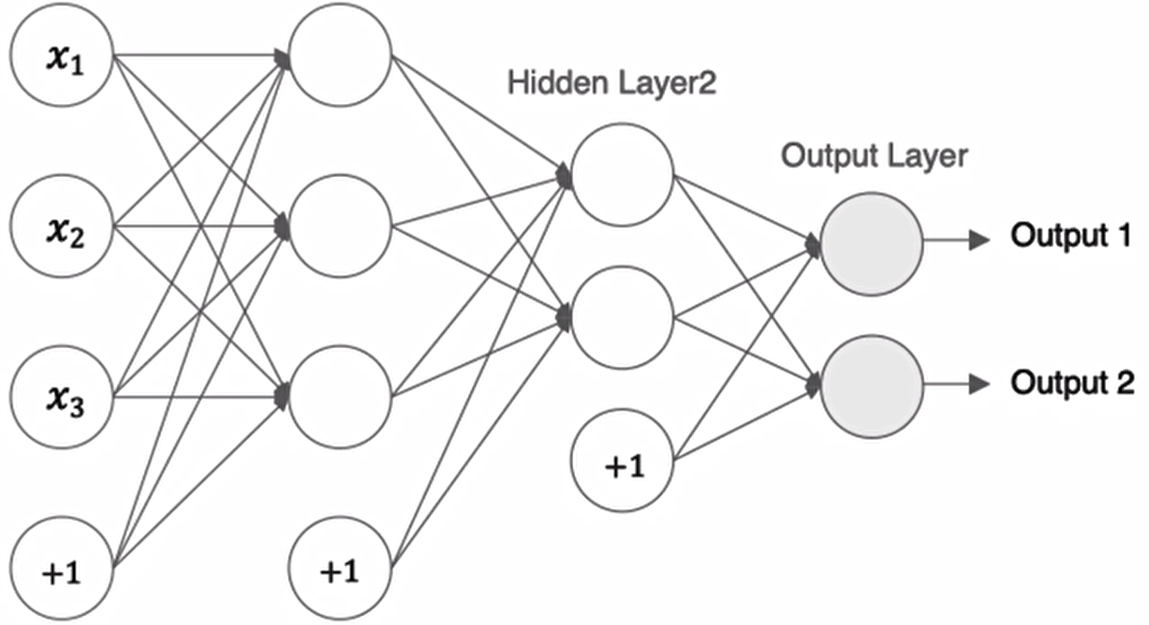
tf.Keras中构建模有两种方式，一种是通过Sequential构建，一种是通过Model类构建。前者是按一定的顺序对层进行堆叠，而后者可以用来构建较复杂的网络模型。首先我们介绍网络全连接层的构建:
tf.keras.layers.Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform',bias_initializer='zeros )- 主要参数:
- units:当前层中包含的神经元个数
- Activation:激活函数，relu,sigmoid等
- kernel_initializer:权重的初始化方式，默认是Xavier初始化
- use_bias:是否使用偏置，默认使用偏置
- bias_initializer: 偏置的初始化方式，默认为0
通过Sequential构建
Sequential() 提供一个层的列表，就能快速地建立一个神经网络模型，实现方法如下所示:
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
# 定义一个Sequential模型，包含三层
model=keras.Sequential([
# 指定输入层参数的形状
layers.Input(shape=(3,1)),
# 第一层，激活函数为：relu，权重初始化函数：glorot_uniform
layers.Dense(3,activation='relu',kernel_initializer='glorot_uniform',use_bias=True, name='layers1'),
# 第二层，激活函数为：relu，权重初始化函数：glorot_uniform
layers.Dense(2,activation='relu',kernel_initializer='glorot_uniform',use_bias=True, name='layers2'),
# 第三层，激活函数为：sigmoid，权重初始化函数：glorot_uniform
layers.Dense(2,activation='sigmoid',kernel_initializer='glorot_uniform',use_bias=True, name='layers3')
])
model.summary()Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ layers1 (Dense) │ (None, 3, 3) │ 6 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layers2 (Dense) │ (None, 3, 2) │ 8 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layers3 (Dense) │ (None, 3, 2) │ 6 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 20 (80.00 B)
Trainable params: 20 (80.00 B)
Non-trainable params: 0 (0.00 B)
model.summary()在 TensorFlow/Keras 中的作用是直观展示神经网络的结构和参数信息，是模型调试和分析的核心工具。核心功能详解参照文末：model.summary()上表Param列的参数个数计算方法：参数总数 = (输入特征数 × 神经元数量) + 神经元数量（偏置）
6=1*3+3
8=3*2+2
6=2*2+2
生成拓扑图：
keras.utils.plot_model(
model,
to_file='model.png', # 输出文件名
show_shapes=True, # ★ 关键：显示维度
show_dtype=True, # 显示数据类型
show_layer_names=True, # 显示层名称
rankdir='TB', # 方向: TB(上下)/LR(左右)
expand_nested=False, # 是否展开嵌套模型
dpi=100 # 图像分辨率
)
keras.utils.plot_model()是比model.summary()更强大的模型可视化工具。它生成模型结构的图形化表示，尤其适合理解复杂神经网络架构。详细解析参照文末：keras.utils.plot_model()
通过这种sequential的方式只能构建简单的序列模型，较复杂的模型没有办法实现
通过function APl构建
tf.keras 提供了 Functional API，建立更为复杂的模型，使用方法是将层作为可调用的对象并返回张量，并将输入向量和输出向量提供给 tf.keras.Model的 inputs 和 outputs 参数，实现方法如下:
# 定义输层c
input=tf.keras.layers.Input(shape=(3,1))
# 隐藏层1：激活函数为relu，其他参数默认
x=tf.keras.layers.Dense(3,activation='relu',name='layer1')(input)
# 隐藏层2：激活函数为relu，其他参数默认
x=tf.keras.layers.Dense(3,activation='relu',name='layer2')(x)
#:输出层：激活函数为sigmoid
output=tf.keras.layers.Dense(2,activation='sigmoid',name='layer3')(x)
# 使用Model来创建模型，明确指定输入和输出
model=tf.keras.Model(inputs=input,outputs=output,name='FunctionAPI_Model')
# 展示模型结果
model.summary()Model: "FunctionAPI_Model"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ input_layer_4 (InputLayer) │ (None, 3, 1) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layer1 (Dense) │ (None, 3, 3) │ 6 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layer2 (Dense) │ (None, 3, 3) │ 12 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layer3 (Dense) │ (None, 3, 2) │ 8 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 26 (104.00 B)
Trainable params: 26 (104.00 B)
Non-trainable params: 0 (0.00 B)通过model的子类构建
通过model的子类构建模型，此时需要在_init_中定义神经网络的层，在call方法中定义网络的前向传播过程，实现方法如下:
#定义Model子类
class MyModel(tf.keras.Model):
#在init方法中定义网络层结构
def __init__(self):
super(MyModel,self).__init__()
# 隐藏层1：激活函数为relu，其他参数默认
self.dense1=tf.keras.layers.Dense(3,activation='relu',name='layer1')
# 隐藏层2：激活函数为relu，其他参数默认
self.dense2=tf.keras.layers.Dense(3,activation='relu',name='layer2')
#:输出层：激活函数为sigmoid
self.dense3=tf.keras.layers.Dense(2,activation='sigmoid',name='layer3')
# 在call方法中完成前向传播
def call(self,inputs):
x=self.dense1(inputs)
x=self.dense2(x)
outputs=self.dense3(x)
return outputs
# 实例化模型
model=MyModel()
# 设置一个输入，调用模型（否则无法使用summary（））
x=tf.ones((1,3))
y=model(x)
print(y)
# 展示模型结果
model.summary()tf.Tensor([[0.5141676 0.5086074]], shape=(1, 2), dtype=float32)
Model: "my_model_9"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ layer1 (Dense) │ (1, 3) │ 12 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layer2 (Dense) │ (1, 3) │ 12 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ layer3 (Dense) │ (1, 2) │ 8 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 32 (128.00 B)
Trainable params: 32 (128.00 B)
Non-trainable params: 0 (0.00 B)注意，使用这种方法创建的模型，无法使用keras.utils.plot_model来绘制拓扑图（只会绘制一个结果，不会绘制出整个架构）
keras.utils.plot_model(
model,
to_file='model.png', # 输出文件名
show_shapes=True, # ★ 关键：显示维度
show_dtype=True, # 显示数据类型
show_layer_names=True, # 显示层名称
rankdir='TB', # 方向: TB(上下)/LR(左右)
expand_nested=False, # 是否展开嵌套模型
dpi=100 # 图像分辨率
)
神经网络的优缺点
1.优点
- 精度高，性能优于其他的机器学习方法，甚至在某些领域超过了人类C
- 可以近似任意的非线性函数
- 随之计算机硬件的发展，近年来在学界和业界受到了热捧，有大量的框架和库可供调用
2.缺点
- 黑箱，很难解释模型是怎么工作的
- 训练时间长，需要大量的计算力
- 网络结构复杂，需要调整超参数
- 小数据集上表现不佳，容易发生过拟合
补充内容
model.summary()
核心功能详解
1. 模型结构可视化
- 层级展示：按顺序列出所有层（输入层、隐藏层、输出层）
- 层级类型：显示每层的类别（Dense, Conv2D, LSTM, Dropout 等）
- 拓扑连接：清晰展示数据流的走向（例如通过
Output Shape变化）
2. 参数统计
- 参数数量 (Param #)：
- 可训练参数（权重 W + 偏置 b）
- 不可训练参数（如 BatchNormalization 的冻结参数）
- 计算公式：
Dense层：Params = (输入神经元数 × 输出神经元数) + 输出神经元数（偏置）Conv2D层：Params = (kernel宽 × kernel高 × 输入通道数 × 输出通道数) + 输出通道数（偏置）
3. 维度变化
- Output Shape：
- 显示数据经过每层后的维度变化
- 例如：
(None, 128)表示 (批大小, 特征维度)
4. 资源概览
- 总参数量 (Total params)：所有层参数总和
- 可训练参数量 (Trainable params)：被优化的参数
- 非训练参数量 (Non-trainable params)：冻结参数（如迁移学习中的预训练层）
输出示例分析
-
结构解读：
- 第 1 层：全连接层（128 个神经元），接收
(None, 784)输入（784 维特征） - 第 2 层：Dropout 层（不改变维度）
- 第 3 层：输出层（10 个神经元，适合十分类）
- 第 1 层：全连接层（128 个神经元），接收
-
参数计算：
dense_1：(784 输入 × 128 神经元) + 128 偏置 = 100,480dense_2：(128 输入 × 10 神经元) + 10 偏置 = 1,290
-
资源总结：
- 总计 101,770 个可训练参数
- 无冻结参数
为什么需要它？
| 场景 | 用途 |
|---|---|
| 模型调试 | 快速发现层维度不匹配错误（如 Conv2D 输出尺寸计算错误） |
| 资源优化 | 识别参数量爆炸的层（如过度复杂的 Dense 层） |
| 架构理解 | 可视化数据流的维度变化（尤其 RNN/CNN 的序列处理） |
| 迁移学习 | 检查冻结参数的数量 |
| 论文/报告 | 提供标准的模型结构描述格式 |
进阶使用技巧
-
自定义输出：
-
获取参数细节：
-
可视化工具扩展：
何时使用？
- 模型构建完成后立即调用
- 加载预训练模型后验证结构
- 出现维度相关错误时诊断问题
- 模型部署前评估计算复杂度
📌 注意：需在模型编译 (
model.compile()) 后调用，否则可能丢失参数量信息（部分层在编译时才确定维度）
keras.utils.plot_model()
核心功能与优势
1. 图形化拓扑结构
- 生成类似流程图的模型结构图
- 显示层级连接关系（单路径/多输入输出/分支结构）
- 直观展示数据流动方向
2. 多层信息集成
| 显示内容 | 说明 | 启用参数 |
|---|---|---|
| 层名称 | 每层的标识名 | 默认显示 |
| 层类型 | Dense/Conv2D/LSTM等 | 默认显示 |
| 输入输出维度 | 每层的 tensor shape | show_shapes=True |
| 数据类型 | float32/int64 等 | show_dtype=True |
| 参数数量 | 每层的可训练参数量 | 需自定义 |
3. 复杂架构支持
- 完美可视化：
- 多输入/多输出模型
- 分支结构（如 Inception 模块）
- 残差连接（ResNet 跳跃连接）
- 共享权重层
- 子模型嵌套
关键参数详解
tf.keras.utils.plot_model(
model,
to_file='model.png', # 输出文件名
show_shapes=True, # ★ 关键：显示维度
show_dtype=False, # 显示数据类型
show_layer_names=True, # 显示层名称
rankdir='TB', # 方向: TB(上下)/LR(左右)
expand_nested=False, # 是否展开嵌套模型
dpi=96 # 图像分辨率
)示例输出与应用场景
1. 简单全连接网络
2. 复杂CNN架构 (启用show_shapes=True)
plot_model(cnn_model, show_shapes=True, rankdir='LR')3. 多输入/输出模型
plot_model(multi_io_model)相比 model.summary() 的核心优势
| 特性 | plot_model() |
model.summary() |
|---|---|---|
| 架构理解 | 图形化拓扑 (⭐️⭐️⭐️⭐️⭐️) | 文本列表 (⭐️⭐️⭐️) |
| 复杂结构展示 | 支持分支/循环 (⭐️⭐️⭐️⭐️⭐️) | 线性描述 (⭐️⭐️) |
| 维度可视化 | 直观显示 shape 变化 | 需自行脑补 |
| 多输入/输出支持 | 清晰展示接口 | 文本混乱 |
| 分享与展示 | 可直接嵌入论文/报告 | 需额外说明 |
高级技巧
导出矢量图 (论文级质量)
plot_model(model, to_file='model.svg') # SVG格式可无损缩放自定义样式
# 安装graphviz后使用DOT语言定制
plot_model(model, show_shapes=True, rankdir='LR', dpi=200)嵌套模型展开
# 显示子模型内部结构
plot_model(meta_model, expand_nested=True)使用场景推荐
- 模型设计阶段：快速验证架构合理性
- 学术论文写作：自动生成出版级结构图
- 团队协作：直观展示模型设计方案
- 调试复杂模型：精确定位维度不匹配的层
- 技术分享/教学：可视化讲解神经网络
⚠️ 依赖项：需安装 Graphviz
You must install pydot (`pip install pydot`) for `plot_model` to work.You must install graphviz (see instructions at https://graphviz.gitlab.io/download/) for `plot_model` to work.安装方法：
pip install pydot && apt-get install graphviz # Linux brew install graphviz # MacOS choco install graphviz # Windows (管理员模式)
如果命令方式安装失败：
通过官方安装器手动安装（推荐）
下载安装包：
https://graphviz.org/download/#windows
→ 选择Stable Windows install packages中的 graphviz-13.0.1 (64-bit) EXE installer [sha256]双击下载的
.exe文件安装
- 安装时勾选 ✅ "Add Graphviz to the system PATH"
验证安装：
dot -V # 应显示版本：dot - graphviz version 13.0.1
浙公网安备 33010602011771号