06.优化算法

前面我们学习了神经网络权重W和偏移b的初始化方法，也知道了不同场景下损失函数的计算方法，那么如何根据损失函数来优化神经网络的参数W和b呢？

梯度下降算法【回顾】

假设需要一条直线来回归拟合三个点：

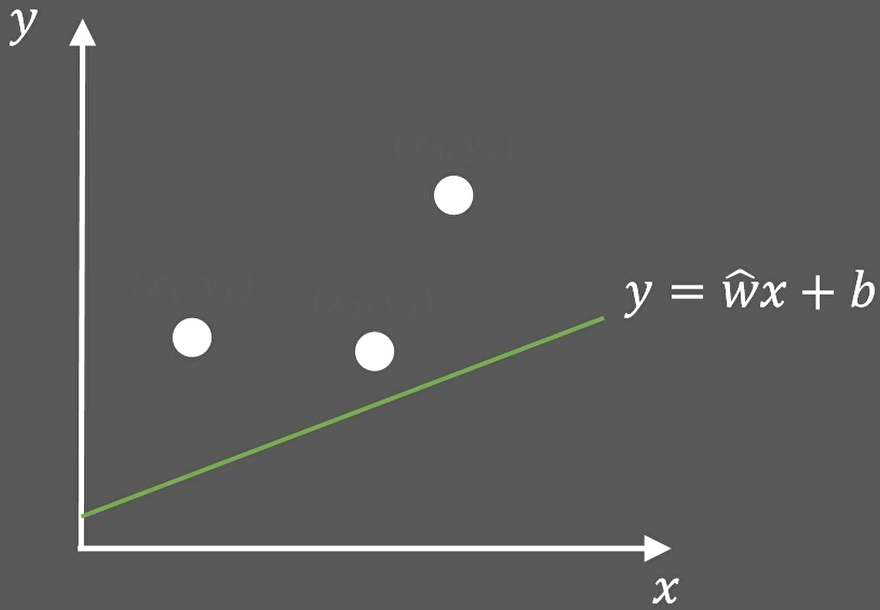
假设直线的斜率w已知，现在要找到一个最好的截距b，使得三个点到直线的距离之和最小：

我们使用最小二乘法表示上面的距离之和：

那么上面的函数就是损失函数，它的大小代表预测值和真实值之间的误差大小。我们的目标就是找到一个b,使这个“误差”也就是损失函数的值最小，这样得到的直线拟合效果最好，我们把直线方程带入损失函数：

上面式子变形为：

从上面的式子可以看出，损失函数L，其实是关于b的一个二次函数。我们假设这个二次函数图像如下，那么我们就可以找到让损失函数最小的b值：

假设一开始我们随便给定一个b值，那么我们如何去求是损失函数最小的那个b值呢？我们可以利用“梯度方向是函数增大最快的方向”这个理论，让b沿着梯度的反方向移动指定长度（ε：学习率，是人为设定的参数，用来控制梯度下降的步长），就会得到新的L：

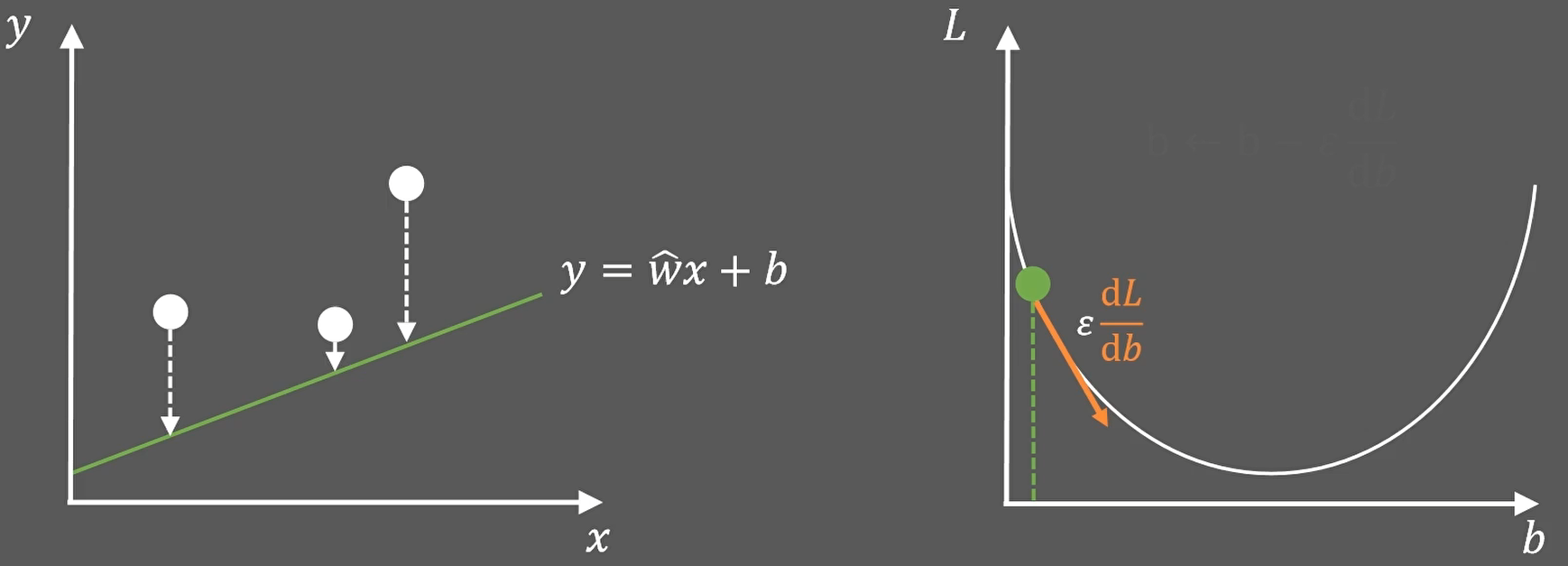
这样，如果L值如果确实比之前更小了，那么就更新b值。

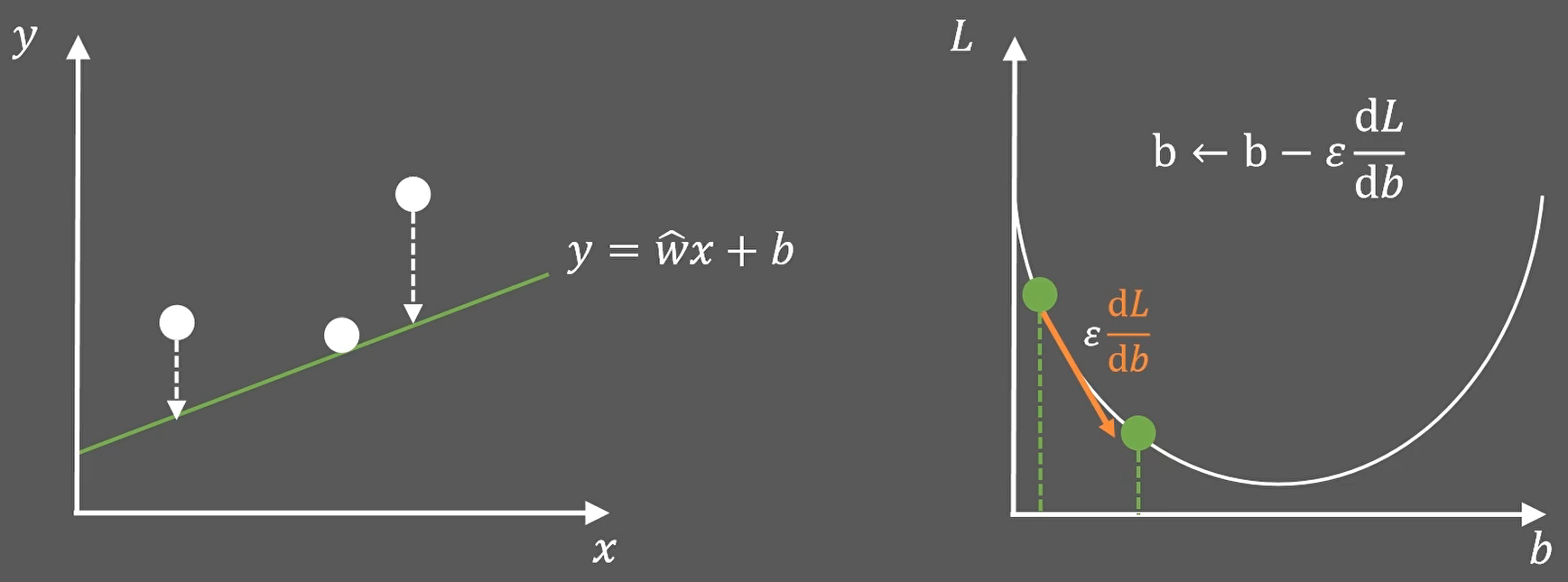
循环往复，直至L取得最小值（本案例中，也就是梯度为0时）：

至此优化过程结束，我们也找到了对应的最优的b值。这就是梯度下降算法；

梯度下降法简单来说就是一种寻找使损失函数最小化的方法。从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向。

现在假设我们要拟合更多的点，拟合线段的形状也从直线变成了曲线，方程也更复杂：

对应的损失函数是：

其中θ就是我们要优化的目标，我们对θ求梯度，并使用g来表示：

那么θ沿着梯度的负方向移动，就可以使损失函数变小了：

ε：学习率，是人为设定的参数，用来控制梯度下降的步长

当然，上面的θ对应到更复杂的曲线函数，其实也就是我们常说的参数数组：ω

在上图中我们展示了一维和多维的损失函数，损失函数呈碗状。在训练过程中损失函数对权重的偏导数就是损失函数在该位置点的梯度。我们可以看到，沿着负梯度方向移动，就可以到达损失函数底部，从而使损失函数最小化。这种利用损失函数的梯度迭代地寻找局部最小值的过程就是梯度下降的过程。

按照上面的思路可以求解出最优解，但是每次参数更新，都需要计算所有样本的梯度值，然后求和、求均值、作差：

在样本量很大时，会带来很大的内存开销，并且收敛速度缓慢。那么如何解决这个问题呢？

答案很简单，那就是每次只用少部分数据参与计算：

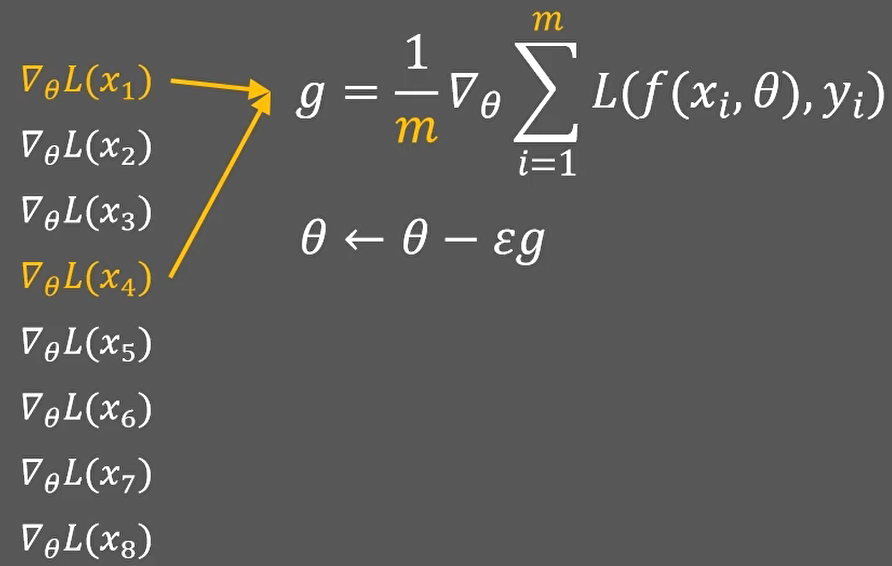
我们假设每次都从n个样本里随机选择m个样本，而且每次都不重复;

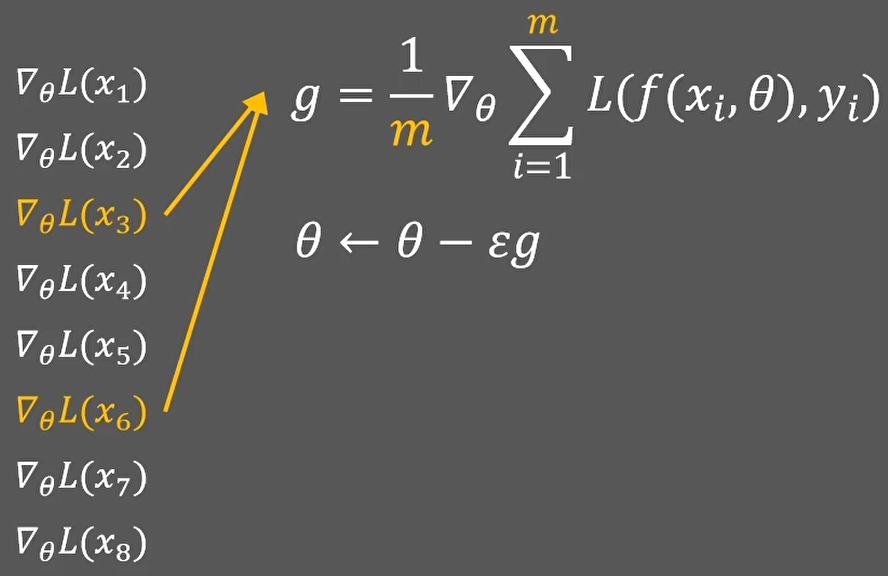
这种改进方法就是小批量梯度下降。m=1的时候就是随机梯度下降。

在样本方差较小的时候，使用少部分样本，虽然会引入噪声，但是仍然可以按照正常的趋势来收敛函数。

经典梯度下降方法分类

根据在进行迭代时使用的样本量，将梯度下降算法分为以下三类:

梯度下降算法	定义	缺点	优点
BGD（批量梯度下降）	每次迭代时需要计算每个样本上损失函数的梯度并求和	计算量大、迭代速度慢	全局最优化
SGD（随机梯度下降）	每次迭代时只采集一个样本，计算这个样本损失函数的梯度并更新参数	准确度下降、存在噪音、非全局最优化	训练速度快、支持在线学习
MBGD（小批量梯度下降）	每次迭代时，我们随机选取一小部分训练样本来计算梯度并更新参数	准确度不如 BGD、非全局最优解	计算小批量数据的梯度更加高效、支持在线学习

经典梯度下降方法API

在tf.keras中实现经典梯度下降的方法：

tf.keras.optimizers.SGD(
    learning_rate=0.1,momentum=0,nesterov=False,name='SGD',**kwards
)

在 TensorFlow 的 Keras API 中，你可以通过 tf.keras.optimizers 模块来实例化不同的优化器，其中就包括 SGD（随机梯度下降）。

需要注意的是，Keras 中并没有直接提供名为 BGD（批量梯度下降）以及MBGD的优化器类，这是因为 BGD 和MBGD实际上是 SGD 的两种情况.

在模型训练时，model.fit(batch_size=？)方法，通过将批量大小（batch_size）设置为整个数据集的大小即可实现BGD；将 batch_size 设置为一个较小的值（如 32、64、128 等）即可实现MBGD。

详情参照下面的综合案例。

简单示例代码：

import tensorflow as tf
# 1. 实例化优化器
opt = tf.keras.optimizers.SGD(learning_rate=0.1)
# 2. 定义要调整的参数
var = tf.Variable([1.0])
# 3. 使用 GradientTape 计算梯度
with tf.GradientTape() as tape:
    # 在 tape 上下文中定义损失函数
    loss = (var ** 2) / 2  # 直接计算，无需 lambda 包装
# 4. 计算梯度
grads = tape.gradient(loss, [var])
# 5. 应用梯度更新参数
opt.apply_gradients(zip(grads, [var]))
# 6. 查看更新后的值
print(var.numpy())  # 输出: [-0.9] 因为 1.0 - 0.1 * 1.0 = -0.9

[0.9]

💡 快速理解梯度更新原理

在您原始代码中，var = tf.Variable([1.0])，损失为 f(var) = var²/2：

梯度 = ∂f/∂var = var

当 var=1.0 时，梯度=1.0

更新公式: var_new = var - learning_rate * gradient

=> var_new = 1.0 - 0.1 * 1.0 = 0.9

第一次更新后，var 变为 0.9

再次运行代码会继续更新：0.9 - 0.1 * 0.9 = 0.81

综合案例：

下面我将展示如何在 Keras 中使用这三种梯度下降方法：

import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.optimizers import SGD

# 加载示例数据集（MNIST 手写数字）
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# 数据预处理
x_train = x_train / 255.0
x_test = x_test / 255.0
y_train = tf.keras.utils.to_categorical(y_train, 10)
y_test = tf.keras.utils.to_categorical(y_test, 10)

# 构建简单的神经网络模型
def create_model():
    model = Sequential([
        Flatten(input_shape=(28, 28)),
        Dense(128, activation='relu'),
        Dense(64, activation='relu'),
        Dense(10, activation='softmax')
    ])
    return model

# 1. 使用 BGD（批量梯度下降）
# 在 Keras 中，通过将 batch_size 设置为整个数据集大小来实现 BGD
model_bgd = create_model()
model_bgd.compile(
    optimizer=SGD(learning_rate=0.01),  # 使用 SGD 优化器
    loss='categorical_crossentropy',
    metrics=['accuracy']
)

# 训练时将 batch_size 设置为数据集大小（这里是 60000）
# 注意：实际应用中，如果数据集很大，BGD 会非常慢
history_bgd = model_bgd.fit(
    x_train, y_train,
    epochs=5,
    batch_size=60000,  # 整个训练集的大小
    validation_data=(x_test, y_test)
)

# 2. 使用 SGD（随机梯度下降）
# 在 Keras 中，将 batch_size 设置为 1 来实现真正的 SGD
model_sgd = create_model()
model_sgd.compile(
    optimizer=SGD(learning_rate=0.01),  # 使用 SGD 优化器
    loss='categorical_crossentropy',
    metrics=['accuracy']
)

# 训练时将 batch_size 设置为 1
history_sgd = model_sgd.fit(
    x_train, y_train,
    epochs=5,
    batch_size=1,  # 每次只使用一个样本更新参数
    validation_data=(x_test, y_test)
)

# 3. 使用 MBGD（小批量梯度下降）
# 在 Keras 中，将 batch_size 设置为一个较小的值（如 32、64、128 等）
model_mbgd = create_model()
model_mbgd.compile(
    optimizer=SGD(learning_rate=0.01),  # 使用 SGD 优化器
    loss='categorical_crossentropy',
    metrics=['accuracy']
)

# 训练时使用常见的 batch_size（如 64）
history_mbgd = model_mbgd.fit(
    x_train, y_train,
    epochs=5,
    batch_size=64,  # 小批量样本
    validation_data=(x_test, y_test)
)

# 比较三种方法的训练过程
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(history_bgd.history['loss'], label='BGD')
plt.plot(history_sgd.history['loss'], label='SGD')
plt.plot(history_mbgd.history['loss'], label='MBGD')
plt.title('Training Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(history_bgd.history['accuracy'], label='BGD')
plt.plot(history_sgd.history['accuracy'], label='SGD')
plt.plot(history_mbgd.history['accuracy'], label='MBGD')
plt.title('Training Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()

plt.tight_layout()
plt.show()

查看训练过程

Epoch 1/5
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 782ms/step - accuracy: 0.0791 - loss: 2.3416 - val_accuracy: 0.0817 - val_loss: 2.3378
Epoch 2/5
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 230ms/step - accuracy: 0.0807 - loss: 2.3346 - val_accuracy: 0.0826 - val_loss: 2.3307
Epoch 3/5
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 227ms/step - accuracy: 0.0827 - loss: 2.3278 - val_accuracy: 0.0856 - val_loss: 2.3238
Epoch 4/5
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 239ms/step - accuracy: 0.0855 - loss: 2.3211 - val_accuracy: 0.0891 - val_loss: 2.3171
Epoch 5/5
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 236ms/step - accuracy: 0.0884 - loss: 2.3146 - val_accuracy: 0.0924 - val_loss: 2.3104
Epoch 1/5
60000/60000 ━━━━━━━━━━━━━━━━━━━━ 76s 1ms/step - accuracy: 0.8887 - loss: 0.3587 - val_accuracy: 0.9599 - val_loss: 0.1302
Epoch 2/5
60000/60000 ━━━━━━━━━━━━━━━━━━━━ 74s 1ms/step - accuracy: 0.9675 - loss: 0.1076 - val_accuracy: 0.9639 - val_loss: 0.1134
Epoch 3/5
60000/60000 ━━━━━━━━━━━━━━━━━━━━ 77s 1ms/step - accuracy: 0.9779 - loss: 0.0720 - val_accuracy: 0.9748 - val_loss: 0.0841
Epoch 4/5
60000/60000 ━━━━━━━━━━━━━━━━━━━━ 80s 1ms/step - accuracy: 0.9820 - loss: 0.0559 - val_accuracy: 0.9603 - val_loss: 0.1320
Epoch 5/5
60000/60000 ━━━━━━━━━━━━━━━━━━━━ 77s 1ms/step - accuracy: 0.9846 - loss: 0.0478 - val_accuracy: 0.9719 - val_loss: 0.1024
Epoch 1/5
938/938 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - accuracy: 0.6309 - loss: 1.3100 - val_accuracy: 0.8911 - val_loss: 0.4083
Epoch 2/5
938/938 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.8915 - loss: 0.3975 - val_accuracy: 0.9102 - val_loss: 0.3172
Epoch 3/5
938/938 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9102 - loss: 0.3163 - val_accuracy: 0.9211 - val_loss: 0.2784
Epoch 4/5
938/938 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9174 - loss: 0.2882 - val_accuracy: 0.9277 - val_loss: 0.2514
Epoch 5/5
938/938 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9268 - loss: 0.2549 - val_accuracy: 0.9313 - val_loss: 0.2338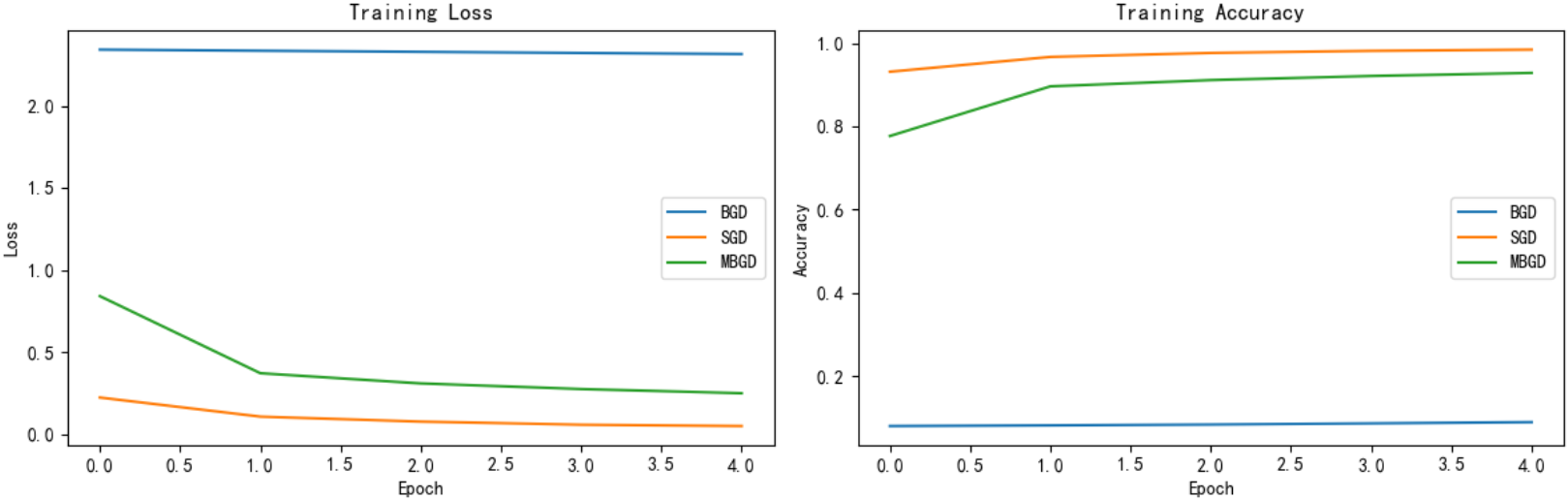

经典梯度下降方法的问题及优化方法

梯度下降算法在进行网络训练时，会遇到收敛速度慢、鞍点、局部极小值、无线震荡等等，这些问题，那我们怎么改进SGD呢?

在这里我们介绍几个比较常用的，在经典三类基础梯度下降方法上的优化：

动量算法(Momentum)

[məˈmentəm]

深度学习网络训练往往是一个非凸的优化过程。在参数空间里，分布着各种山脊和山谷。在梯度下降过程中，如果学习率设置过大，（步长过大），那么参数就会无限循环（在极值点附近来回震荡）：

按照上面的情况，很难收敛到最低点。

如果学习率太小，那么每次训练之后得到的效果都太小，增大训练的时间成本。如果，学习率太大，那就有可能直接跳过最优解，进入无限的训练中。

解决思路：如果能够给每次梯度更新时，添加一些阻尼就好了（可能就不会跳过最优解了），在下一次梯度更新时，我们不仅要计算新的梯度，还要保留上一次一部分的梯度：

我们把保留的历史梯度称为动量，这个改进方法也被称为“使用动量的随机梯度下降”。

物理理解：

参数的移动，受到来自梯度的一个“力”，但是它任然要保留原始运动状态的一部分速度，这样运动起来才更符合物理规律，这也是动量的物理含义。

数学表述：

逻辑：给梯度更新 “加惯性”，保留一部分上一轮的更新方向，公式：

作用：减少梯度震荡（如 SGD 来回波动），加速收敛（尤其在 “长平坡” 区域）。

为什么在“长平坡”区域SGD会慢？

在标准SGD中，更新公式是：参数更新 = 学习率 × 当前梯度。

问题：如果梯度很小（“平坡”），更新步长也很小，导致每次参数只移动一点点。

结果：优化器需要很多次迭代才能通过这个区域，收敛速度慢（收敛指找到损失函数的最小值）。

动量算法如何加速收敛，尤其在“长平坡”区域？

动量算法（如SGD with Momentum）通过引入一个“动量项”（momentum term）来模拟物理中的惯性：

动量公式：更新方向不只看当前梯度，还加权平均过去梯度（指数加权移动平均）。

简单来说：动量项会“记住”和“积累”过去梯度的方向。

在“长平坡”区域的作用：

虽然当前梯度小，但方向相对一致（例如一直为正或负），动量项会累积这些微小但方向一致的梯度，形成一个较大的“推动力”。

这就像在斜坡上推雪球：在平坡上，雪球越滚越大（动量积累），速度越来越快（步长增大），帮助你更快下坡。

效果：

减少慢速蠕动：在平坡上，SGD可能每步只移动0.001，动量算法可能每步移动0.1（因为累积的动量放大了一致的梯度）。

加速通过平坡：整体收敛更快（实验证明，动量算法可让收敛速度提升几倍或更多）。

类似在震荡区域（如“陡峭山谷”）时，动量也能平滑方向变化，减少来回震荡。

API

在tf.keras中使用Momentum算法仍使用功能SGD方法，但要设置momentum参数，实现过程如下:

import tensorflow as tf

# 1. 实例化优化器 (带动量)
opt = tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9)

# 2. 定义参数
var = tf.Variable([1.0])
var0 = var.numpy()

# 3. 第一次更新 (重新计算梯度)
with tf.GradientTape() as tape:
    loss1 = (var ** 2) / 2
grads1 = tape.gradient(loss1, [var])
opt.apply_gradients(zip(grads1, [var]))
var1 = var.numpy()

# 4. 第二次更新 (用新的变量值重新计算)
with tf.GradientTape() as tape:
    loss2 = (var ** 2) / 2
grads2 = tape.gradient(loss2, [var])
opt.apply_gradients(zip(grads2, [var]))
var2 = var.numpy()

# 5. 输出结果
print(f'初始值: {var0}')
print(f'第一次更新后: {var1}')
print(f'第二次更新后: {var2}')
print(f'第一次更新步长: {var1 - var0}')
print(f'第二次更新步长: {var2 - var1}')

初始值: [1.]
第一次更新后: [0.9]
第二次更新后: [0.71999997]
第一次更新步长: [-0.10000002]
第二次更新步长: [-0.18]

步长增大：动量优化会累积历史梯度（第二次步长大于第一次）
梯度变化：第二次更新基于新位置(0.9)重新计算梯度

动态跟踪优化过程：

import tensorflow as tf
# 1. 实例化优化器 (带动量)
opt = tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9)

var = tf.Variable([1.0])
for step in range(10):
    with tf.GradientTape() as tape:
        loss = (var ** 2) / 2
    grads = tape.gradient(loss, [var])
    opt.apply_gradients(zip(grads, [var]))
    print(f"Step {step+1}: var={var.numpy()}, loss={loss.numpy()}")

Step 1: var=[0.9], loss=[0.5]
Step 2: var=[0.71999997], loss=[0.40499997]
Step 3: var=[0.486], loss=[0.25919998]
Step 4: var=[0.22680002], loss=[0.118098]
Step 5: var=[-0.02915996], loss=[0.02571912]
Step 6: var=[-0.25660795], loss=[0.00042515]
Step 7: var=[-0.43565035], loss=[0.03292382]
Step 8: var=[-0.5532235], loss=[0.09489562]
Step 9: var=[-0.60371697], loss=[0.15302812]
Step 10: var=[-0.58878934], loss=[0.18223709]

另外还有一种动量算法Nesterov accelerated gradient(NAG)，使用了根据动量项**预先估计**的参数，在Momentum的基础上进一步加快收敛，提高响应性，该算法实现依然使用SGD方法，要设置nesterov设置为true.

AdaGrad

2011年诞生的算法

先看一下原始的梯度下降方式更新参数的方式：

ε：学习率，是人为设定的参数，用来控制梯度下降的步长

一般情况，我们希望神经网络最开始快速找到收敛方向，会设置一个比较大的学习率，而随着训练过程的深入，我们在训练后期最重要的目标是找到最优解，而不能再盲目追求速度了，而是让网络更加细致的优化，防止损失函数剧烈震荡。

解决的方法就是，学习率也需要随着训练的进行而变化。所以我们需要给学习率设置一个初始值，然后每隔一段时间就降低学习率。

但是如果依靠手动调整学习率，不现实。那么能不能让学习率随着梯度的变化动态调整呢？

于是我们可以尝试引入一个新的变量r（r是梯度大小随时间的积累量）：

如果把根号r（√r）放在学习率的分母上，那么梯度波动很大的时候（说明一下子快要下到底了），学习率就会快速的下降（赶紧减小学习率，小步向前），而梯度波动很小的时候，学习率下降也会慢一些：

分母中的δ是一个极小数值，如10^(-6），用来防止分母为0，稳定数值计算

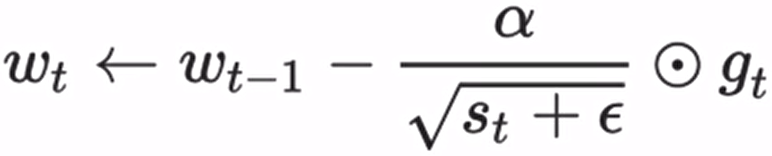
其中a是学习率，ε是为了维持数值稳定性而添加的常数如10^(-6）。这里开方、除法和乘法的运算都是按元素运算的。这些按元素运算使得目标函数自变量中每个元素都分别拥有自己的学习率

API
在tf.keras中的实现方法是:

tf.keras.optimizers.Adagrad(learning_rate=0.1,initial_accumulator_value=0.1,epsilon=1e-07)

参数详解：

参数名称 作用 默认值 影响范围 调整建议 典型场景

参数名称	作用	默认值	影响范围	调整建议	典型场景
learning_rate (学习率)	控制参数更新的基础幅度	0.001	全局更新。在 Adagrad 中，实际学习率会随时间衰减。	↑ 收敛慢时增大 ↓ 震荡时减小	常见于 Adagrad 0.01-0.1 (Adagrad 需更高学习率，通常比其他优化器(SGD/Adam)的学习率更大)
initial_accumulator_value (初始累加值)	初始化梯度平方累加器 G 的初始值	0.1	训练初期稳定性实际学习率 = learning_rate / sqrt(G + epsilon) 当 G≈初始值0.1时：实际学习率 ≈ 0.1 / √0.1 ≈ 0.316	↑ 震荡时增大(0.5) ↓ 缓慢时减小(0.01) 值越大 → 初始学习率越小，稳定性越好值越小 → 初始学习率越大，收敛越快	决定实际初始学习率： `实际学习率 = learning_rate / sqrt(initial_accumulator_value)+epsilon`
epsilon (极小值)	防止分母为零的稳定项	1e-07	极小梯度区域	基本无需调整 ↑ 数值错误时略增大(1e-06)	训练初期当累加值≈0时提供数值保护

learning_rate
(学习率)

控制参数更新的基础幅度

0.001

全局更新。

在 Adagrad 中，实际学习率会随时间衰减。

↑ 收敛慢时增大
↓ 震荡时减小

常见于 Adagrad

0.01-0.1 (Adagrad 需更高学习率，通常比其他优化器(SGD/Adam)的学习率更大)

initial_accumulator_value
(初始累加值)

初始化梯度平方累加器 G 的初始值

0.1

训练初期稳定性

实际学习率 = learning_rate / sqrt(G + epsilon)

当 G≈初始值0.1时：实际学习率 ≈ 0.1 / √0.1 ≈ 0.316

↑ 震荡时增大(0.5)
↓ 缓慢时减小(0.01)

值越大 → 初始学习率越小，稳定性越好
值越小 → 初始学习率越大，收敛越快

决定实际初始学习率：
实际学习率 = learning_rate / sqrt(initial_accumulator_value)+epsilon

epsilon
(极小值) 防止分母为零的稳定项 1e-07 极小梯度区域基本无需调整
↑ 数值错误时略增大(1e-06) 训练初期当累加值≈0时
提供数值保护

示例代码：

# 1. 实例化优化器
opt = tf.keras.optimizers.Adagrad(learning_rate=0.1,initial_accumulator_value=0.1,epsilon=1e-07)

# 2. 定义要调整的参数
var = tf.Variable([1.0])
# 3. 使用 GradientTape 计算梯度
with tf.GradientTape() as tape:
    # 在 tape 上下文中定义损失函数
    loss = (var ** 2) / 2 
# 4. 计算梯度
grads = tape.gradient(loss, [var])
# 5. 应用梯度更新参数
opt.apply_gradients(zip(grads, [var]))
# 6. 查看更新后的值
print(var.numpy())  # [0.9046537]

思考：AdaGrad算法里，学习率的变化之和梯度有关，可能会导致学习率过早变小，而且不好控制。所以2012年提出了RMSprop算法。

RMSprop

AdaGrad算法在迭代后期由于学习率过小,较难找到最优解。为了解决这一问题，RMSProp算法对AdaGrad算法做了一点小小的修改：在r更新的公式中加入了可以手动调节的rho

作用：解决 “学习率一刀切” 问题，让更新更平滑，适合非凸优化。

最终自变量每个元素的学习率在迭代过程中就不再一直降低。RMSProp有助于减少抵达最小值路径上的摆动，并允许使用一个更大的学习率ε，从而加快算法学习速度。

API

在tf.keras中的实现方法是:

tf.keras.optimizers.RMSprop(learning_rate=0.1,rho=0,momentum=0,epsilon=1e-07,centered=False,name='RMSprop',**kwargs)

示例代码：

# 1. 实例化优化器
opt = tf.keras.optimizers.RMSprop(learning_rate=0.1)

# 2. 定义要调整的参数
var = tf.Variable([1.0])
# 3. 使用 GradientTape 计算梯度
with tf.GradientTape() as tape:
    # 在 tape 上下文中定义损失函数
    loss = (var ** 2) / 2 
# 4. 计算梯度
grads = tape.gradient(loss, [var])
# 5. 应用梯度更新参数
opt.apply_gradients(zip(grads, [var]))
# 6. 查看更新后的值
print(var.numpy())  # [0.6837724]

Adam（使用较多，小白首选）

2014年提出

Adam 优化算法(Adaptive Moment Estimation，自适应矩估计)将Momentum和 RMSProp 算法结合在一起。

并且上面两个参数分别可以通过参数beta_1和beta_2控制，并且会在训练之初，修正这两个参数，让他们比较大，帮助算法快速收敛：

最终的参数更新公式为：

建议的参数设置的值:

学习率ε:需要尝试一系列的值，来寻找比较合适的
B1:常用的缺省值为 0.9
B2:建议为 0.999
e:默认值1e-8

在tf.keras中实现的方法是：

tf.keras.optimizers.Adam(learning_rate=0.1,beta_1=0.9,beta_2=0.999,epsilon=1e-07)

示例代码：

# 1. 实例化优化器
opt = tf.keras.optimizers.Adam(learning_rate=0.1)

# 2. 定义要调整的参数
var = tf.Variable([1.0])
# 3. 使用 GradientTape 计算梯度
with tf.GradientTape() as tape:
    # 在 tape 上下文中定义损失函数
    loss = (var ** 2) / 2 
# 4. 计算梯度
grads = tape.gradient(loss, [var])
# 5. 应用梯度更新参数
opt.apply_gradients(zip(grads, [var]))
# 6. 查看更新后的值
print(var.numpy())  # [0.900001]

梯度下降算法总结

梯度下降算法(Gradient Descent,GD)，深度学习核心之一
随机梯度下降算法(Stochastic Gradient Descent,SGD)
动量(Moment)
自适应学习 AdaGrad和RMSProp 算法
动量 & 自适应学习 Adam

反向传播算法(BP算法）

先看一个线性拟合的例子：

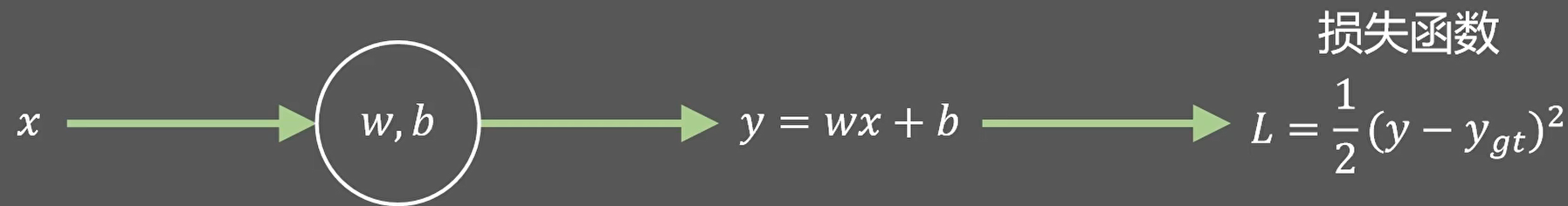
y_gt：真实值

假设已知：

假设真实值是0.8，那么损失函数L=（1.4-0.8）²/2=0.18

那么我们该如何调整优化w和b呢？

根据上面讲的梯度下降算法，我们需要计算损失函数L相对于w和b的梯度值，也就是L相对于w和b的偏导数，然后沿着梯度的反方向更新两个参数就可以了：

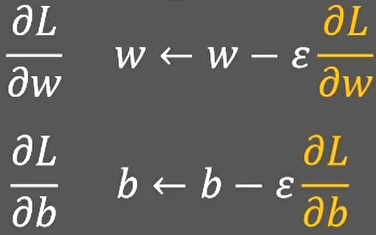
为了更容易计算w和b的偏导，我们先计算一个中间量，就是L对y的偏导，这样L对w的偏导就可以写作，L对y的偏导乘以y对w的偏导，这就是“链式法则”。

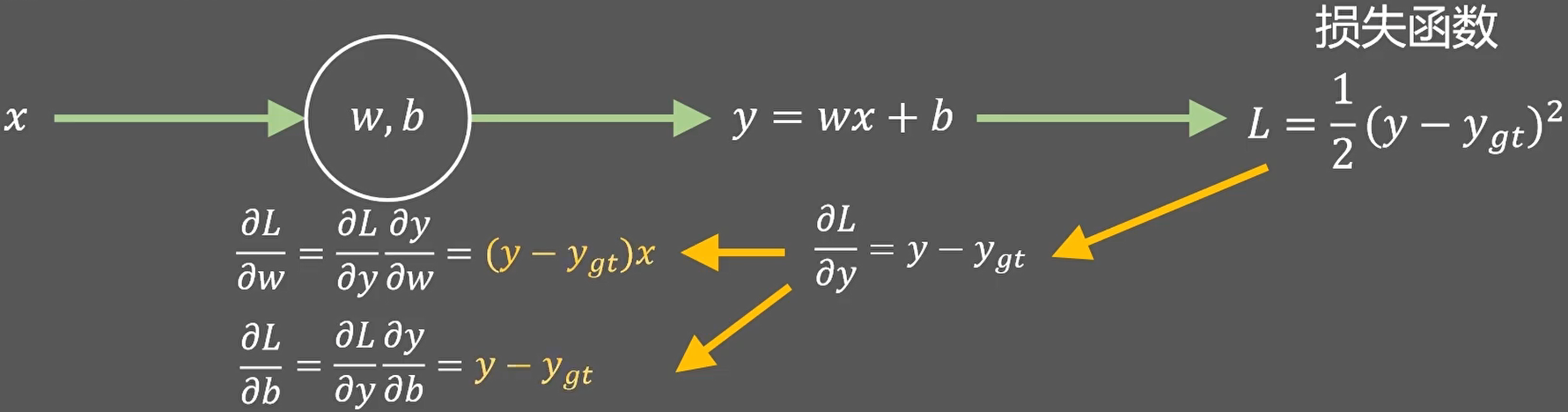
通过这种从后向前的求解方式，我就可以得到参数梯度的解析式了。

将y和y_gt以及x带人上述解析式得：

假设学习率为0.1，经过梯度下降算法后，新的w和b就更新成0.71和0.14了，然后可以计算新的y值为：1.205，更加靠近真实值0.8。而且损失函数更小了=0.082。

这种从后往前计算参数梯度值的方法就是反向传播算法。

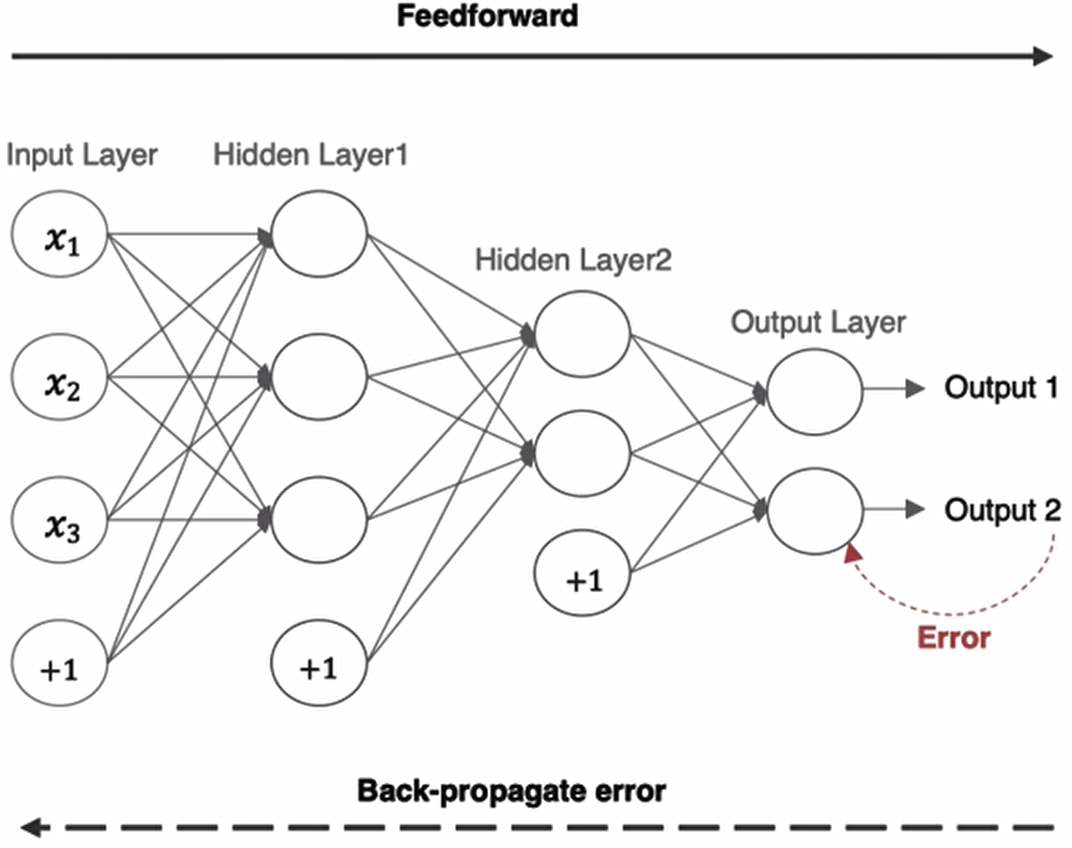
在网络的训练过程中经过前向传播后得到的最终结果跟训练样本的真实值总是存在一定误差，这个误差便是损失函数。想要减小这个误差，就用损失函数ERROR（LOSS），从后往前，依次求各个参数的偏导，这就是反向传播(Back Propagation)。

现在假设在多层神经网络中，存在如下变换：

为了得到w1,b1,w2,b2这四个参数的梯度，我们可以从后向前，计算出损失函数L对于每一个参数的梯度值：

上面黄色标注的梯度值是上一步已经计算出来的梯度值，不需要重复计算了！

所以我们可以这样理解：

反向传播算法，就是神经网络加速计算参数梯度值的方法！

然而计算机中的实际计算过程却并非如此。在计算机中，反向传播算法一般是使用计算图的方式进行模块化运算：

观察上面的式子我们不难发现，一个复合函数，无论如何嵌套，都可以拆分成最简单的相加或相乘运算。只不过每个单元输入的变量不同而已。这种由单元运算和变量构成的流程图也被称为计算图。

我们现在利用计算图来反向求出损失函数对于每个变量的梯度表达式（随便看下，有省略步骤，别被绕晕了，理解思路就行）：

黄色的值就是前面步骤已经计算出的值，绿色的值是向前传播时求得的值。这些值都是已知的。因此可以直接计算出L对于w1,b1,w2,b2这四个参数的梯度值，然后就可以进行参数更新了。

在深度学习框架中，所有的单元运算都有定义好的向前传播和向后传播函数，这样就可可以利用反向传播算法来更新数以亿计的网络参数了，以torch框架为例：

利用反向传播算法对神经网络进行训练，与梯度下降算法相结合，对网络中所有权重（w）计算损失函数的梯度，并利用梯度值来更新权值，以最小化损失函数。

总结

反向传播算法(Back-Propagation, BP)，深度学习核心之一
加速计算参数梯度值的方法
计算图(Computation Graphs)

扩展内容

前向传播与反向传播

前向传播指的是数据输入的神经网络中，逐层向前传输，一直到运算到输出层为止。

在网络的训练过程中经过前向传播后得到的最终结果跟训练样本的真实值总是存在一定误差，这个误差便是损失函数。想要减小这个误差，就用损失函数ERROR，从后往前，依次求各个参数的偏导，这就是反向传播(Back Propagation)。

反向传播算法另一种讲解

反向传播算法利用链式法则对神经网络中的各个节点的权重（w）进行更新。我们通过一个例子来给大家介绍整个流程，假设当前前向传播的过程如下图所以:

计算损失函数，并进行反向传播：

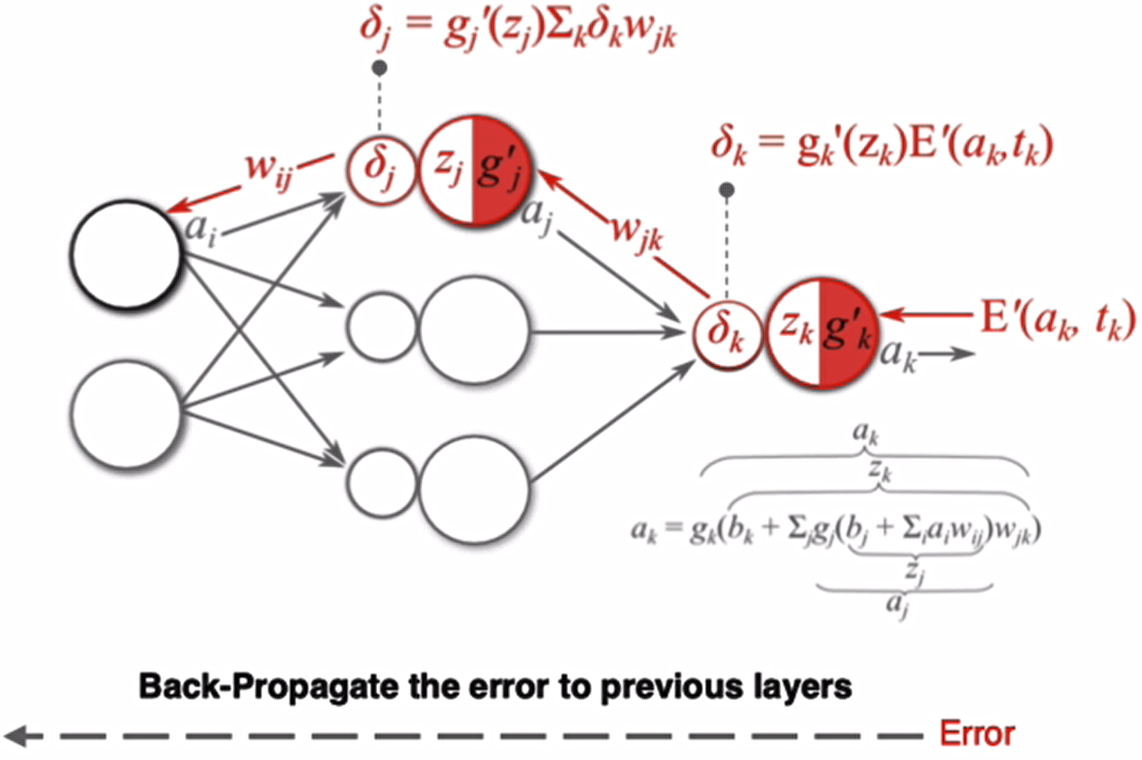
计算梯度值：

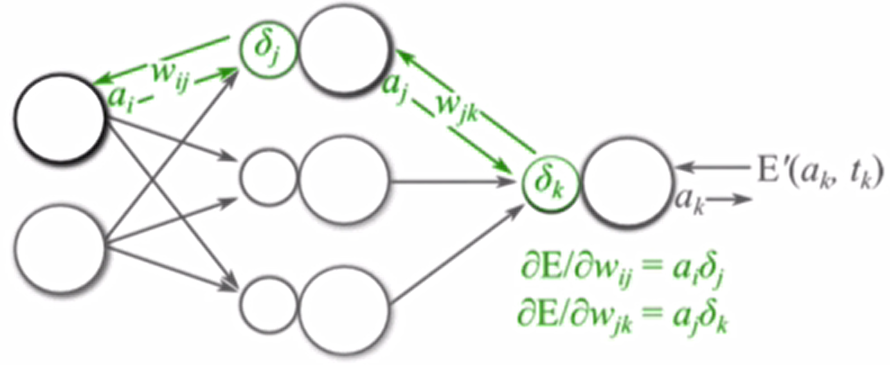
输出层梯度值：

隐藏层梯度值：

偏置的梯度值：

参数更新：

输出层权重：

隐藏层权重：

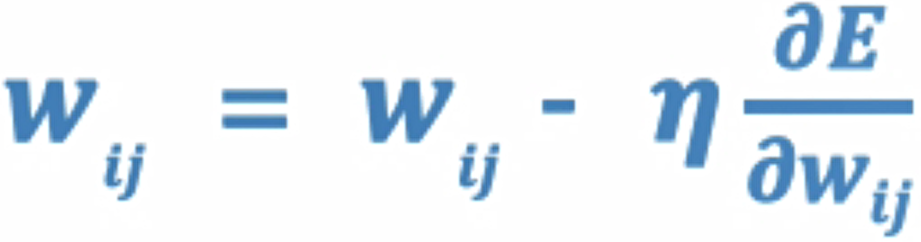
偏置更新：

重复上述过程完成模型训练，整个流程如下表：

链式法则

求导的链式法则本质上就是复合函数求导的规则，不过要更精准理解，得区分不同场景下的表现：

1. 单变量函数：链式法则 = 复合函数求导规则

对单变量复合函数

，链式法则明确了求导方法：

也就是 “外函数对中间变量的导数，乘以内函数对自变量的导数” 。比如

，拆成

（外函数，

是内函数），导数就是

。这时候，链式法则完全等同于单变量复合函数的求导规则，是一回事。

2. 多变量函数：链式法则是复合函数求导的 “拓展版”

当涉及多变量复合函数（比如

），链式法则会更复杂：

这其实是 “复合函数求导规则在多变量场景的推广” ，本质还是通过 “逐层求导再传递” 的逻辑，把复杂复合关系拆解成简单导数的组合。比如神经⽹络里的多层感知机，每层的参数更新就依赖多变量链式法则（反向传播算法的数学基础）。

3. 总结：链式法则是复合函数求导的 “通用解法”

对单变量复合函数，链式法则 直接就是求导规则 ，一步拆成内外函数导数相乘。
对多变量复合函数，链式法则 拓展了求导规则 ，变成 “各中间变量导数的加权和”，但核心逻辑（逐层拆解、传递导数）不变。

所以可以说：链式法则是复合函数求导的核心规则体系 ，涵盖了单变量、多变量等不同场景下复合函数的求导方法，是微积分里处理 “函数嵌套求导” 的通用武器～

链式法则详解

反向传播算法是利用链式法则进行梯度求解及权重更新的。对于复杂的复合函数，我们将其拆分为-系列的加减乘除或指数，对数，三角函数等初等函数，通过链式法则完成复合函数的求导。为简单起见，这里以一个神经网络中常见的复合函数的例子来说明这个过程.令复合函数 f(x;w,b)为:

其中x是输入数据，w是权重，b是偏置。我们可以将该复合函数分解为:

并进行图形化表示，如下：

整个复合函数 f(x;w,b)关于参数w和b的导数可以通过 f(x;w,5)与参数w和b之间路径上所的导数连乘来得到，即:

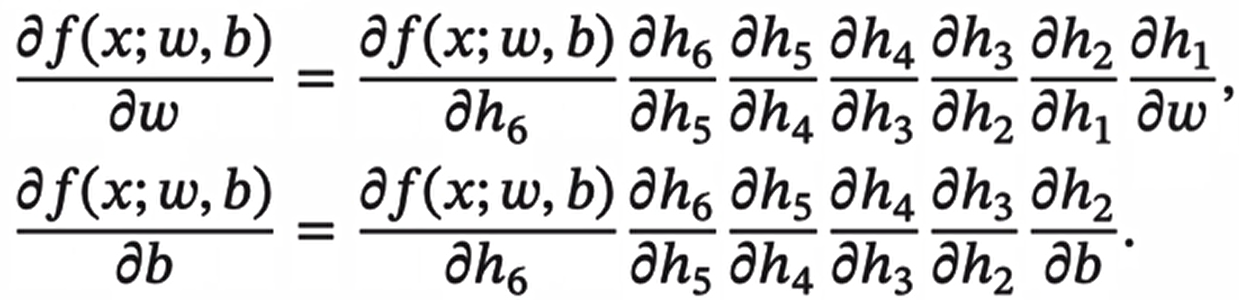
以w为例，当x=1,w=0,b=0时，可以得到:

常用函数的导数：

学习率退火

在训练神经网络时，一般情况下学习率都会随着训练而变化，这主要是由于，在神经网络训练的后期，如果学习率过高，会造成loss的振荡，但是如果学习率减小的过快，又会造成收敛变慢的情况。

分段常数衰减

分段常数衰减是在事先定义好的训练次数区间上，设置不同的学习率常数。刚开始学习率大一些之后越来越小，区间的设置需要根据样本量调整,，一般样本量越大区间间隔应该越小。

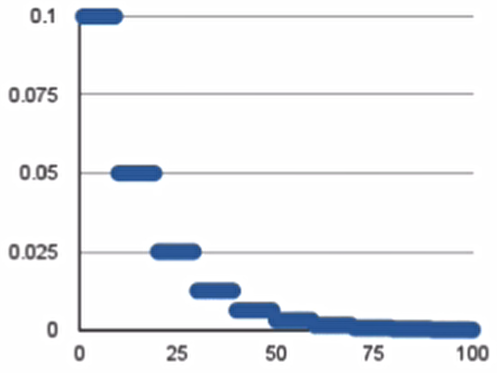
在tf.keras中实现的方法是：

tf.keras.optimizers.schedules.PiecewiseConstantDecay(boundaries,values)

参数：

Boundaries:设置分段更新的step值
Values:针对不用分段的学习率值

例子:对于前100000步，学习率为1.0，对于接下来的100000-110000步，学习率为0.5，之后的步骤学习率为0.1:

#设置的分段的step值
boundaries =[100000,1100001]
# 不同的step对应的学习率
values =[1.0,0.5,0.1]
# 实例化进行学习的更新
learning_rate_fn = keras.optimizers.schedules.PiecewiseConstantDecay(boundaries,values)

指数衰减

指数衰减可以用如下的数学公式表示

其中，t表示迭代次数，a₀,k是超参数

在tf.keras中实现的方法是：

tf.keras.optimizers.schedules.ExponentialDecay(initial_learning_rate,decay_steps,decay_rate)

具体实现是：

def decay_learning_rate():
    return initial_learning_rate*decay_rate^(step/decay_steps)

参数:

Initial_learning_rate:初始学习率，a0
decay_steps: k值
decay_rate:指数的底

1/t衰减

1/t衰减可以用如下的数学公式表示:

其中，t表示迭代次数，a0,k是超参数

参数:

Initial_learning_rate:初始学习率，a0
decay_step/decay_steps: k值

总结

知道梯度下降算法

一种寻找使损失函数最小化的方法:批量梯度下降，随机梯度下降，小批量梯度下降

理解神经网络的链式法则

复合函数的求导

掌握反向传播算法(BP算法)神经网络进行参数更新的方法

知道梯度下降算法的优化方法动量算法，adaGrad,RMSProp,Adam

了解学习率退火

分段常数衰减，指数衰减，1/t衰减

动量法相关知识概念扩充（了解）

指数加权平均

假设给定一个序列，例如北京一年每天的气温值，图中蓝色的点代表真实数据

这时温度值波动比较大，那我们就使用加权平均值来进行平滑，如下图红线就是平滑后的结果:

计算方法如下所示：

其中Yt为t时刻时的真实值，St为t加权平均后的值，β为权重值。红线即是指数加权平均后的结果。
上图中β设为0.9，那么指数加权平均的计算结果为:

S₁=Y₁
S₂=0.9S₁+ 0.1Y₂

...

S₉₉ =0.9S₉₈ + 0.1Y₉₉

S₁₀₀ =0.9S₉₉ + 0.1Y₁₀₀

...

那么第100天的结果就可以表示为：
S₁₀₀=0.1Y₁₀₀+0.1*0.9Y₉₉+0.1*(0.9)²Y₉₈ +...

指数加权平均

动量梯度下降(Gradient Descent with Momentum)计算梯度的指数加权平均数，并利用该值来更新参数值。动量梯度下降法的整个过程为：

β是动量系数，通常设置为0.9:

与原始梯度下降算法相比，动量梯度的下降更平滑：

posted @ 2025-06-28 11:13 指尖下的世界阅读(13) 评论(0) 收藏举报

刷新页面返回顶部

指尖下的世界

今日事今日毕,今日无事早休息.

06.优化算法

梯度下降算法【回顾】

经典梯度下降方法分类

经典梯度下降方法API

简单示例代码：

综合案例：

经典梯度下降方法的问题及优化方法

动量算法(Momentum)

AdaGrad

RMSprop

Adam（使用较多，小白首选）

梯度下降算法总结

反向传播算法(BP算法）

扩展内容

前向传播与反向传播

反向传播算法另一种讲解

链式法则

链式法则详解

学习率退火

分段常数衰减

指数衰减

1/t衰减

动量法相关知识概念扩充（了解）