05.损失函数

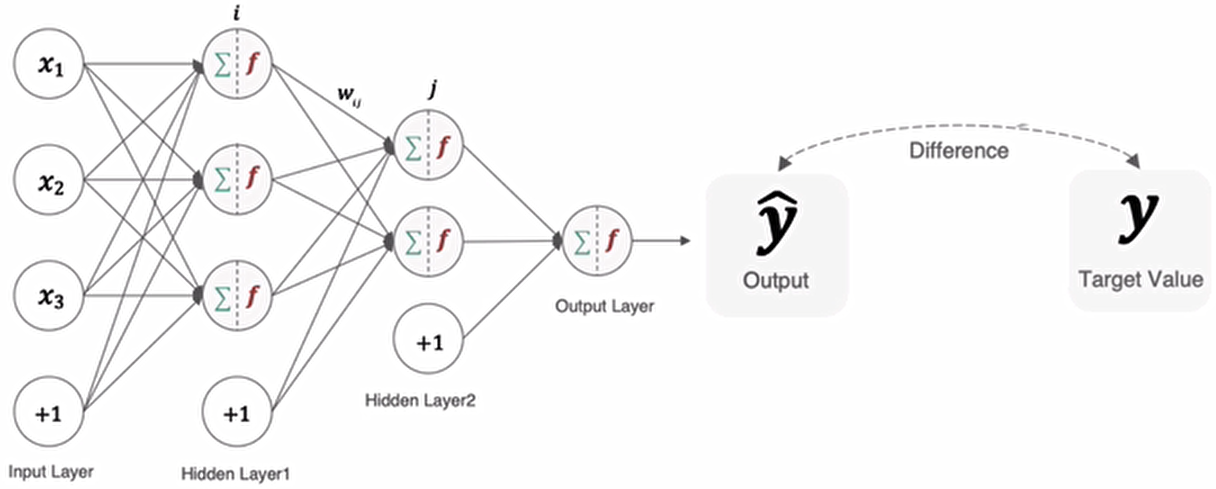
在深度学习中,损失函数是用来衡量模型参数的质量的函数,衡量的方式是比较网络输出和真实输出的差异，损失函数在不同的文献中名称是不一样的，主要有以下几种命名方式:

分类任务

在深度学习的分类任务中使用最多的是交叉熵损失函数，所以在这里我们着重介绍这种损失函数。

多分类任务

在神经网络中，输出层的原始输出（未经过激活函数的数值）被称为logits（可以理解为 “类别分数”，取值范围为 (-∞, +∞)，不满足概率的归一化要求）。为了将 logits 转换为符合要求的概率分布，多分类任务通常使用softmax 函数。softmax直白来说就是将网络输出的logits通过softmax函数，就映射成为(0,1)的值，而这些值的累和为1(满足概率的性质)，那么我们将它理解成概率，选取概率最大(也就是值对应最大的)节点，作为我们的预测目标类别。所以多分类的交叉熵损失也叫做softmax损失，它的计算方法是:

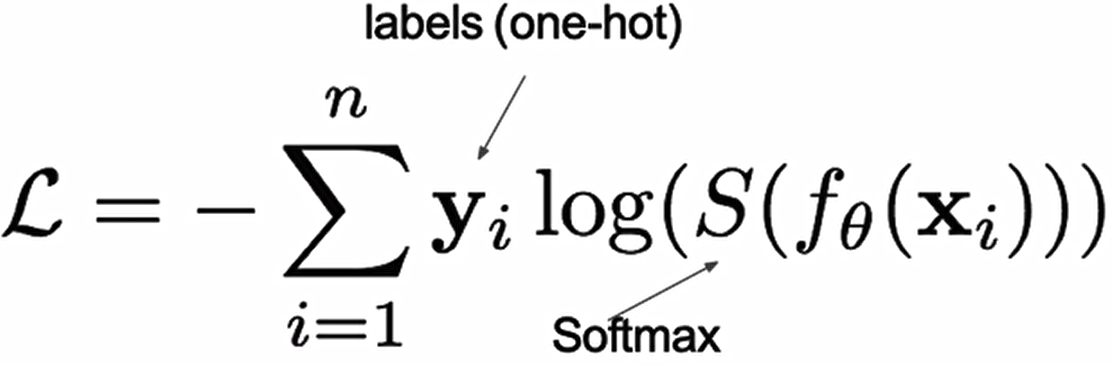
其中，y是样本x属于某一个类别的真实概率（要么1要么0），而f(x)是样本属于某一类别的预测分数，S是softmax函数，将f(x)转换为总和是1的概率，

例子:

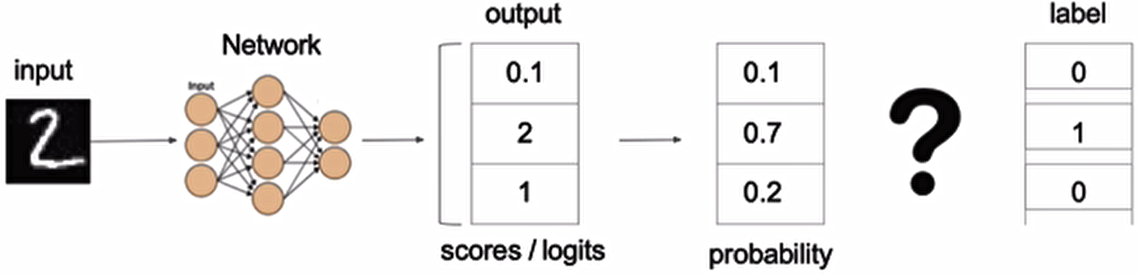
上图中的交叉熵损失为：

从概率角度理解，我们的目的是最小化正确类别所对应的预测概率的对数的负值，如下图所示：

在tf.keras中使用CategoricalCrossentropy实现，如下所示：

# 设置真实值和预测值
y_true=[[0,1,0],[0,0,1]]
y_pre=[[0.1,0.8,0.1],[0.2,0.3,0.5]]
# 实例化交叉熵损失函数
cce=tf.keras.losses.CategoricalCrossentropy()
# 计算损失值
cce(y_true=y_true,y_pred=y_pre).numpy()

0.45814535

二分类任务

在处理二分类任务时，我们不在使用softmax激活函数，而是使用sigmoid激活函数，那损失函数也相应的进行调整，使用二分类的交叉熵损失函数:

其中，y是样本x属于某一个类别的真实概率，而y^是样本属于某一类别的预测概率，L用来衡量真实值与预测值之间差异性的损失结果。
在tf.keras中实现时使用BinaryCrossentropy()，如下所示:

# 设置真实值和预测值
y_true=[0,1]
y_pre=[0.1,0.9]
# 实例化交叉熵损失函数
cce=tf.keras.losses.BinaryCrossentropy()
# 计算损失值
cce(y_true=y_true,y_pred=y_pre).numpy()

0.105360545

回归任务

回归任务中常用的损失函数有以下几种:

MAE损失

Mean absolute loss(MAE)也被称为L1 Loss，是以绝对误差作为距离:

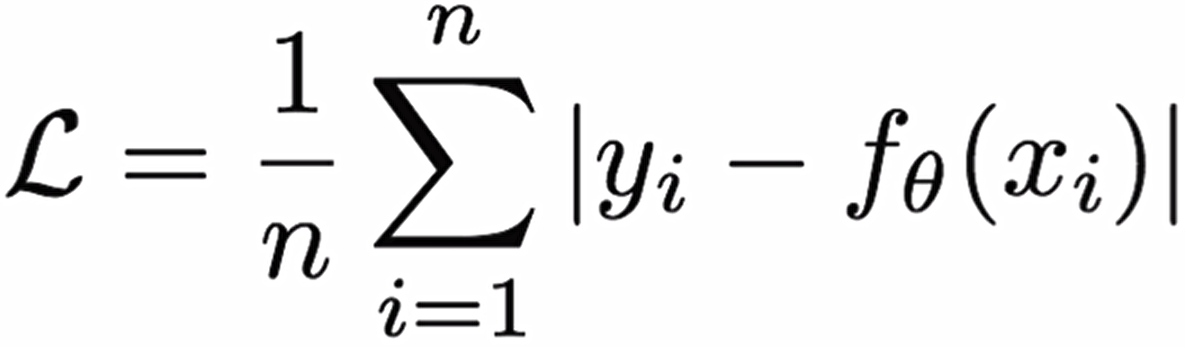
曲线如下：

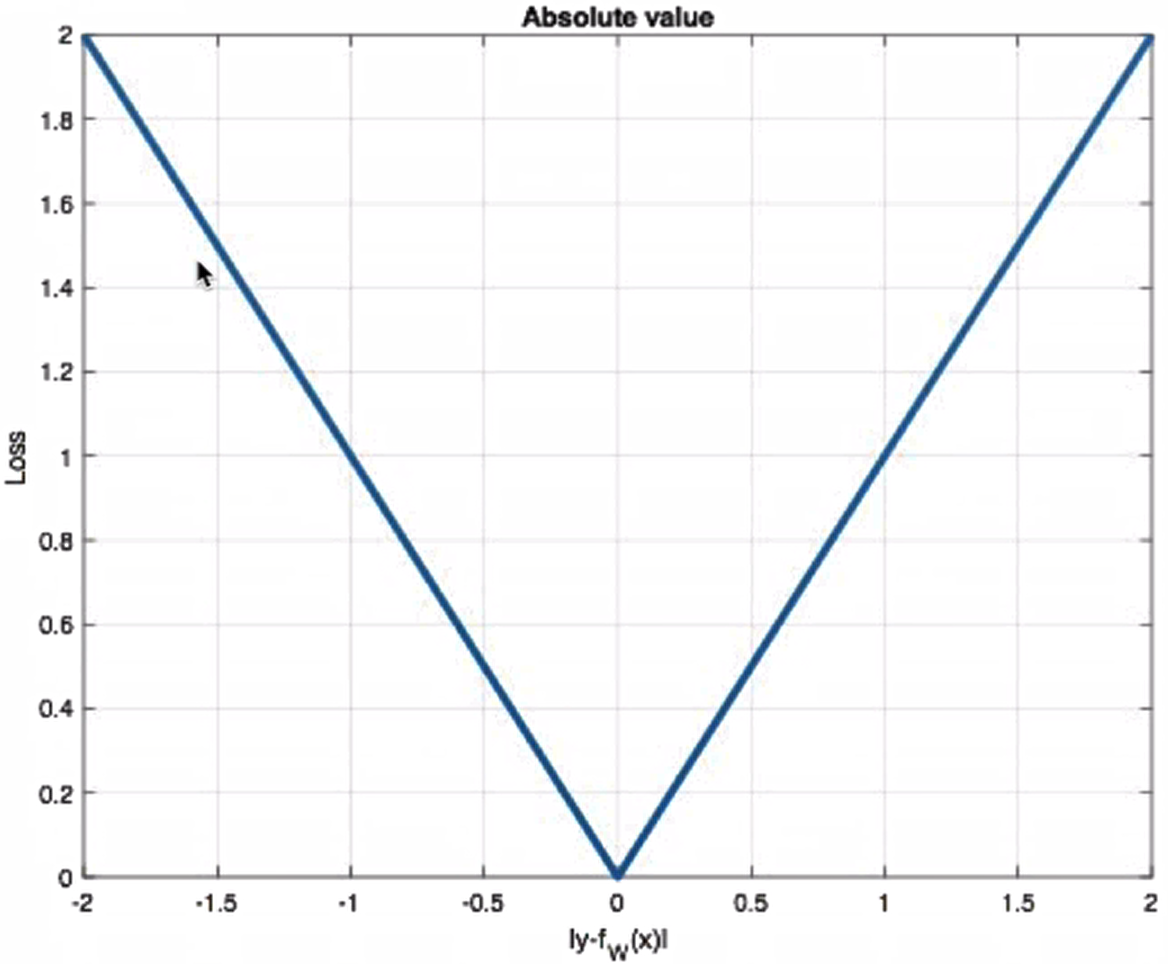
特点是:由于L1loss具有稀疏性，为了惩罚较大的值，因此常常将其作为正则项添加到其他loss中作为约束。L1loss的最大问题是梯度在零点不平滑，导致会跳过极小值。
在tf.keras中使用MeanAbsoluteError实现，如下所示:

# 设置真实值和预测值
y_true=[0,0]
y_pre=[1,1]
# 实例化交叉熵损失函数
cce=tf.keras.losses.MeanAbsoluteError()
# 计算损失值
cce(y_true=y_true,y_pred=y_pre).numpy()

1.0

MSE损失

Mean Squared Loss/ Quadratic Loss(MSEloss)也被称为L2loss，或欧氏距离，它以误差的平方和作为距离:

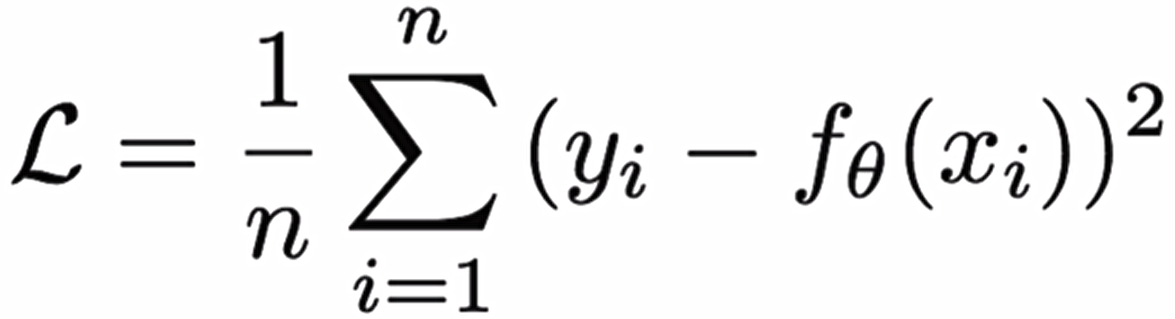
曲线如下：

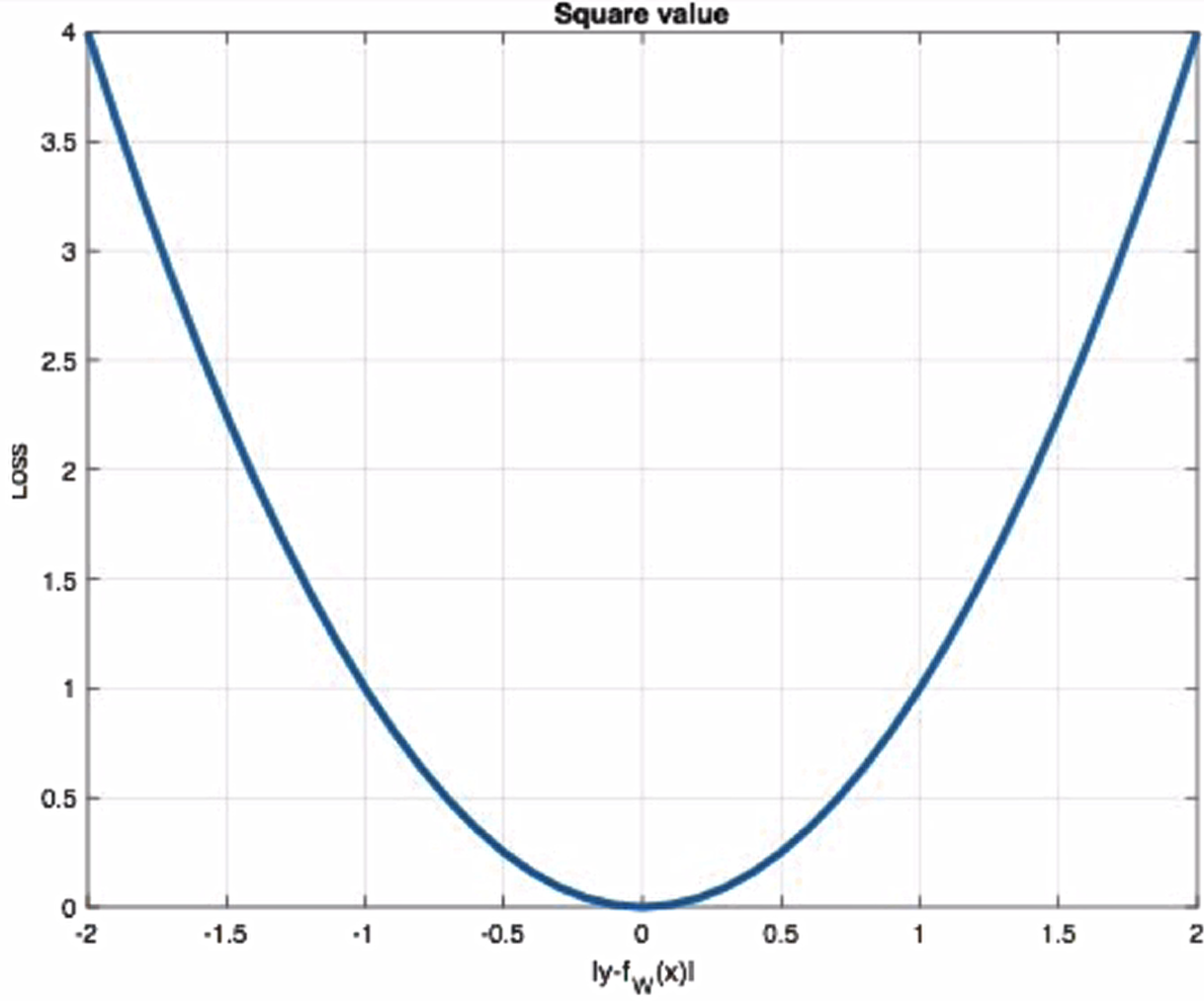
特点是:L2loss也常常作为正则项。当预测值与目标值相差很大时,梯度容易爆炸。在tf.keras中通过MeanSquaredError实现:

# 设置真实值和预测值
y_true=[0,0]
y_pre=[1,1]
# 实例化交叉熵损失函数
cce=tf.keras.losses.MeanSquaredError()
# 计算损失值
cce(y_true=y_true,y_pred=y_pre).numpy()

1.0

smooth L1 损失

Smooth L1损失函数如下式所示:

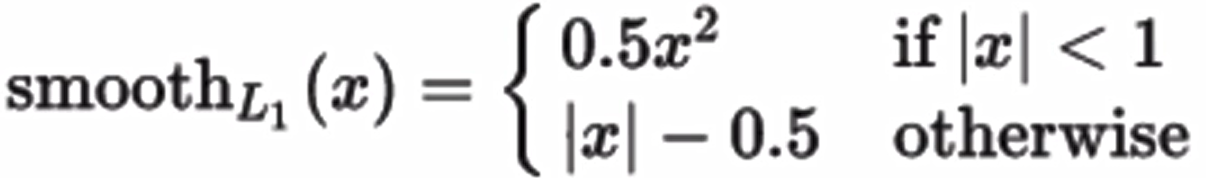
其中:x=f(x)-y 为真实值和预测值的差值

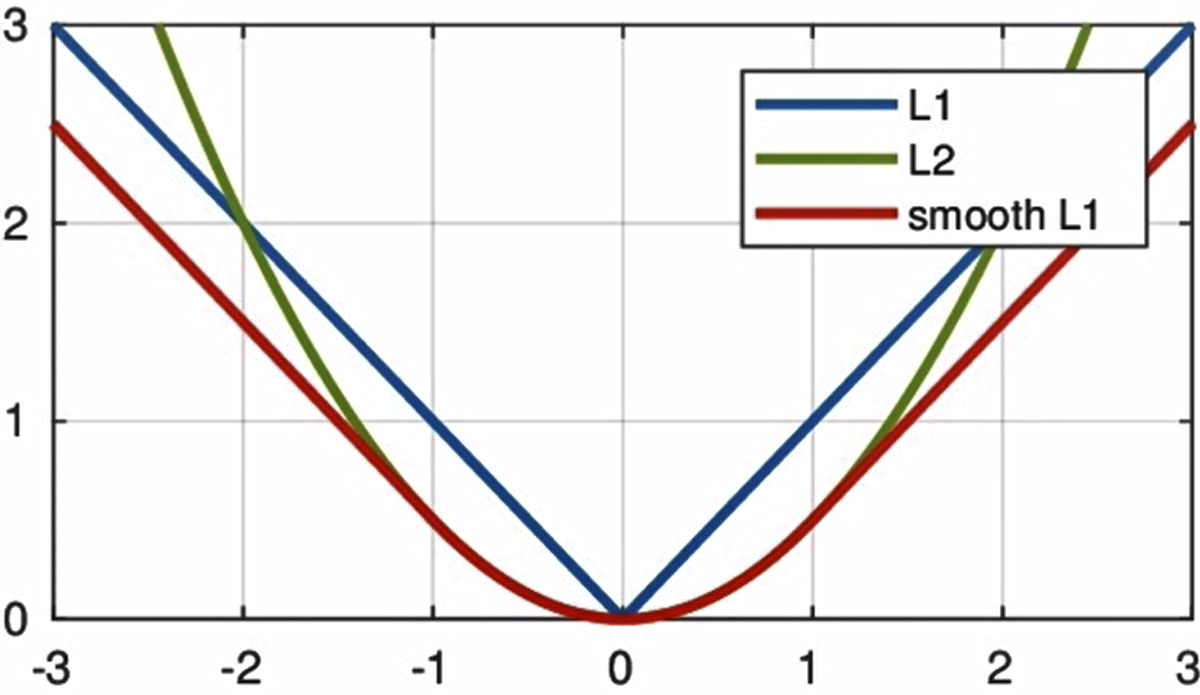
从上图中可以看出，该函数实际上就是一个分段函数，在[1,1]之间实际上就是L2损失，这样解决了L1的不光滑问题，在[1,1]区间外，实际上就是L1损失，这样就解决了离群点梯度爆炸的问题。通常在目标检测中使用该损失函数。
在tf.keras中使用Huber计算该损失，如下所示:

# 设置真实值和预测值
y_true=[0,0]
y_pre=[1,1]
# 实例化交叉熵损失函数
cce=tf.keras.losses.Huber()
# 计算损失值
cce(y_true=y_true,y_pred=y_pre).numpy()

0.5