07.激活函数
激活函数是神经网络中的核心组件,决定了神经元的输出形式和非线性特性。
一、认识激活函数
神经元是如何工作的?
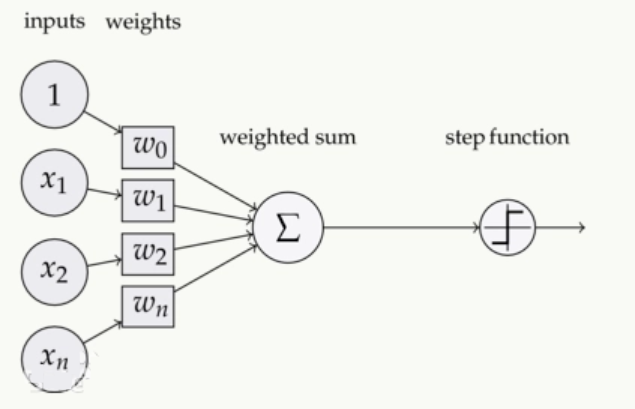
神经元接收到一个或多个输入,对他们进行加权并相加,总和通过一个非线性函数(激活函数)产生输出。
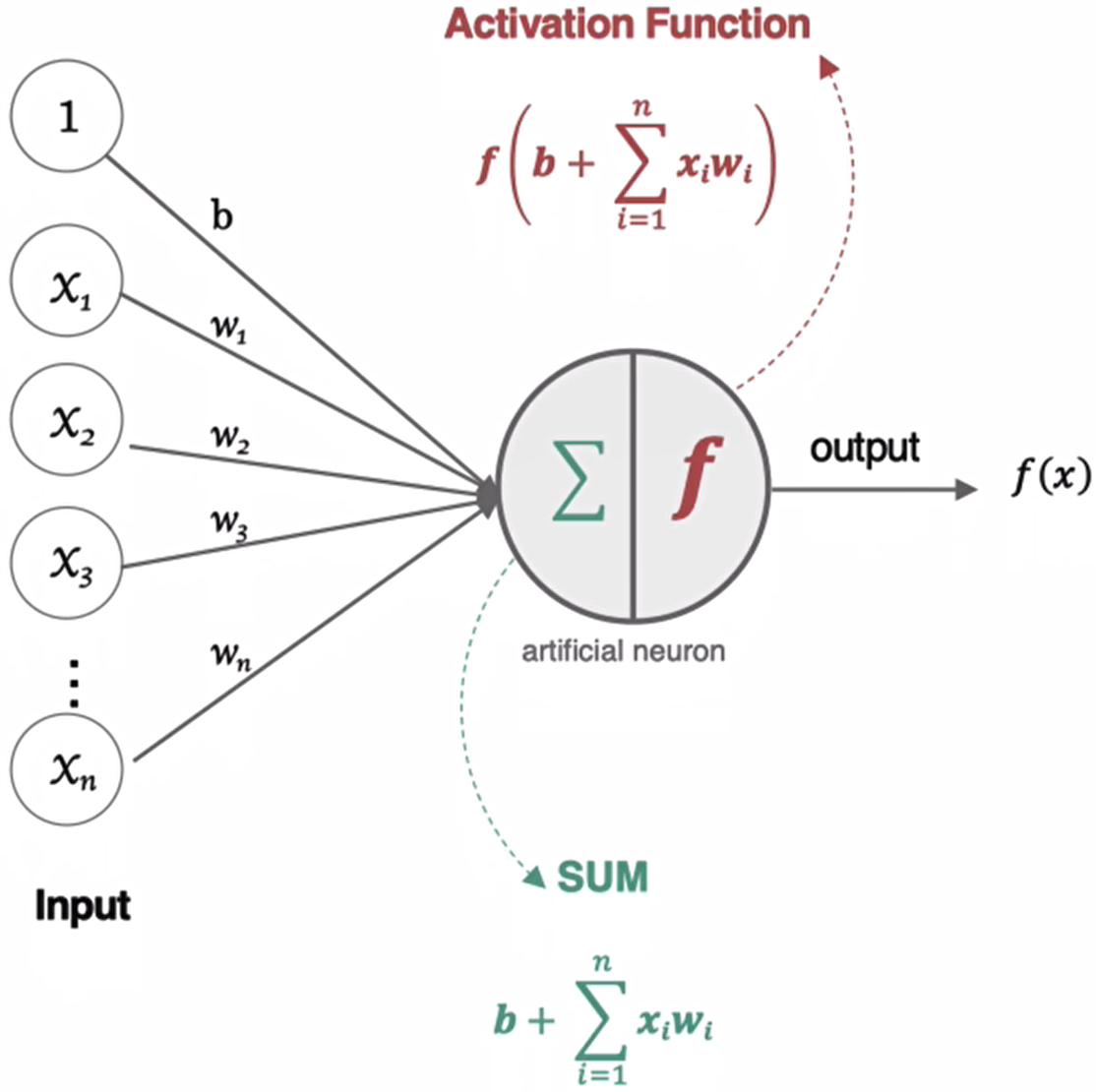
激活函数(Activation Function),就是在神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
在神经元中引入了激活函数,它的本质是向神经网络中引入非线性因素的,通过激活函数,神经网络就可以拟合各种曲线。如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,引入非线性函数作为激活函数,那输出不再是输入的线性组合,可以逼近任意函数。
为什么激活函数要是非线性的?理解:
给定一个线性变换可以把x的值映射到一条直线上:y1=w1x+b1
如果y1在经过线性变换得到y2,那么x和y2也是线性关系:
也就是说无论使用多少次线性变换:
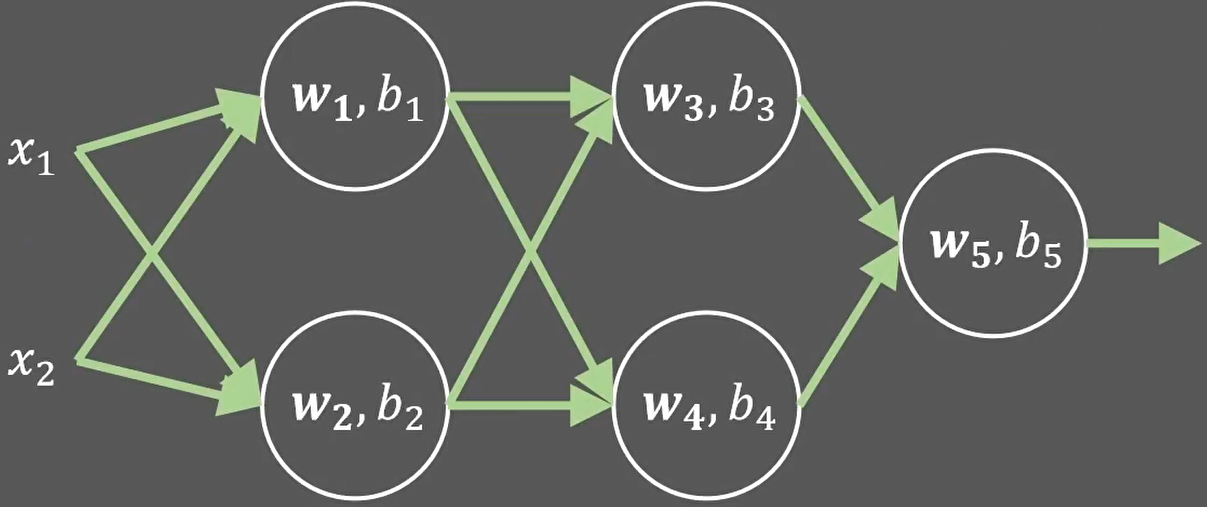
或者把他们叠加成神经网络:
最终只能解决线性问题。
那么应该怎么修改才能让他们解决非线性问题呢?
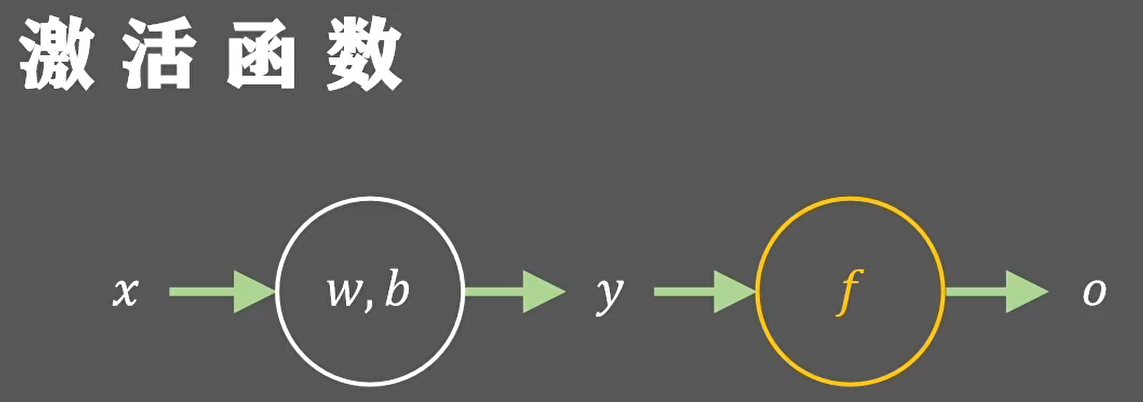
答案就是在线性单元后面再增加一个非线性函数就可以了:
如下图,在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
作用:
- 引入非线性:没有激活函数,神经网络只是线性变换的叠加(无论多少层,等效于单层线性模型)。
- 控制输出范围:例如将输出压缩到0-1(Sigmoid)或-1到1(Tanh)。
- 梯度传播:合适的激活函数能缓解梯度消失或爆炸问题,加速训练。
性质
- 非线性:让模型表现能力更强
- 单调性,可微性,输出值范围是有限的
- 常见的激活函数:Sigmoid Tanh Relu 等
对激活函数的要求
- 连续可导(因为反向传播和梯度进行参数更新时,需要计算出相关导数)
- 定义域是R(为了数值稳定,要能够映射所有实数)
- 单调递增的S型曲线(因为只是对结果进行缩放,不能改变原有输入的响应状态)
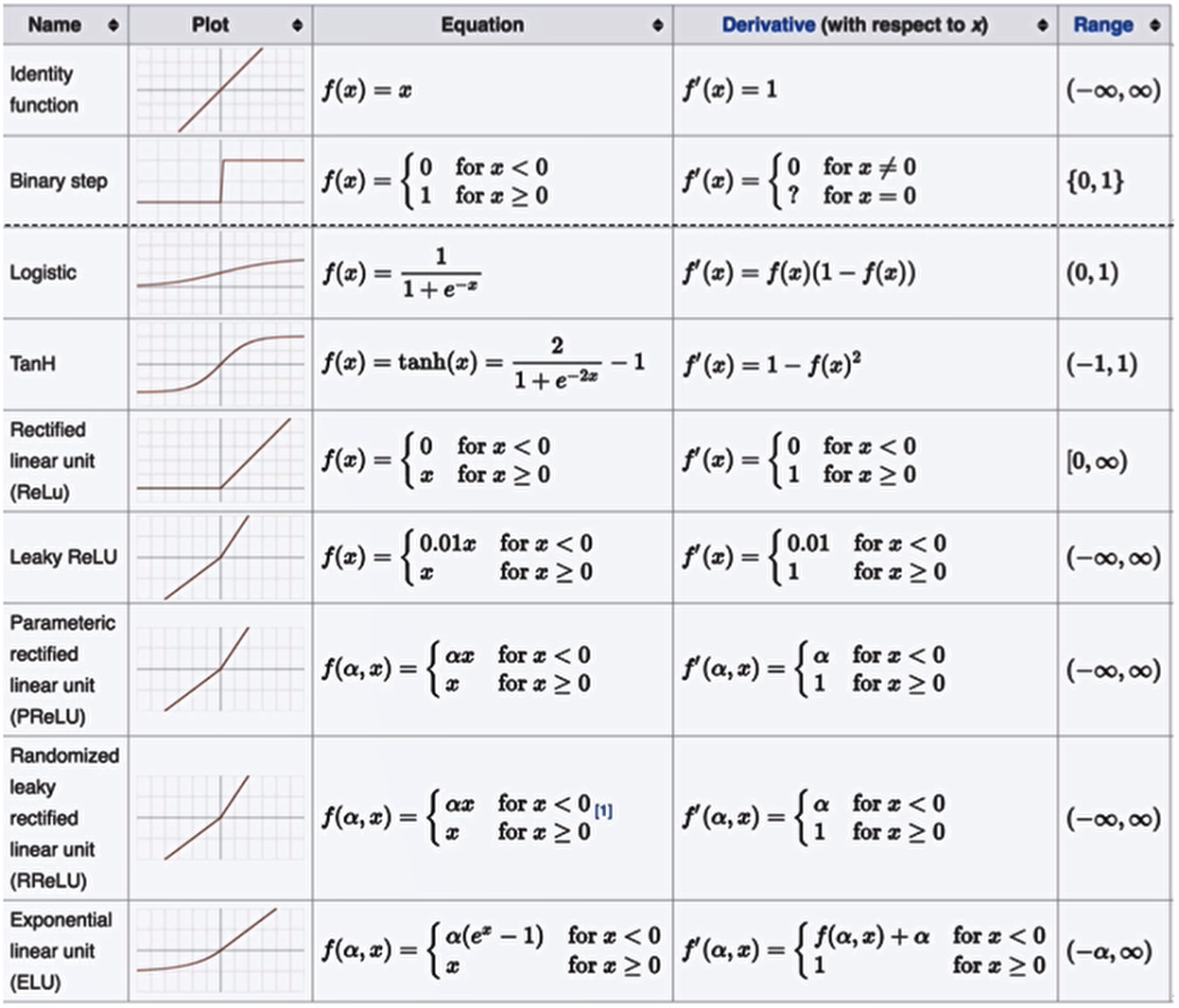
二、常见激活函数详解
1. Sigmoid(Logistic函数)
Sigmoid 是常用的非线性的激活函数,能够把连续值压缩到0-1区间上。

sigmoid 在定义域内处处可导,且两侧导数逐渐趋近于0。如果X的值很大或者很小的时候,那么函数的梯度(函数的斜率)会非常小,在反向传播的过程中,导致了向低层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说,sigmoid 网络在 5层之内就会产生梯度消失现象。而且,该激活函数并不是以0为中心的,所以在实践中这种激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。
- 公式:
- 输出范围:(0, 1):非零均值函数

-
特点:
- 常用于二分类输出层,表示概率。
- 梯度在两端饱和(导数趋近0),导致梯度消失。
- 计算量大(含指数运算)。
-
梯度公式(推导后):
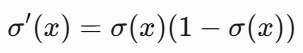
- 缺点1:杀死梯度,非原点中心对称(会导致优化更新会产生阶梯式情况)
梯度消失现象:
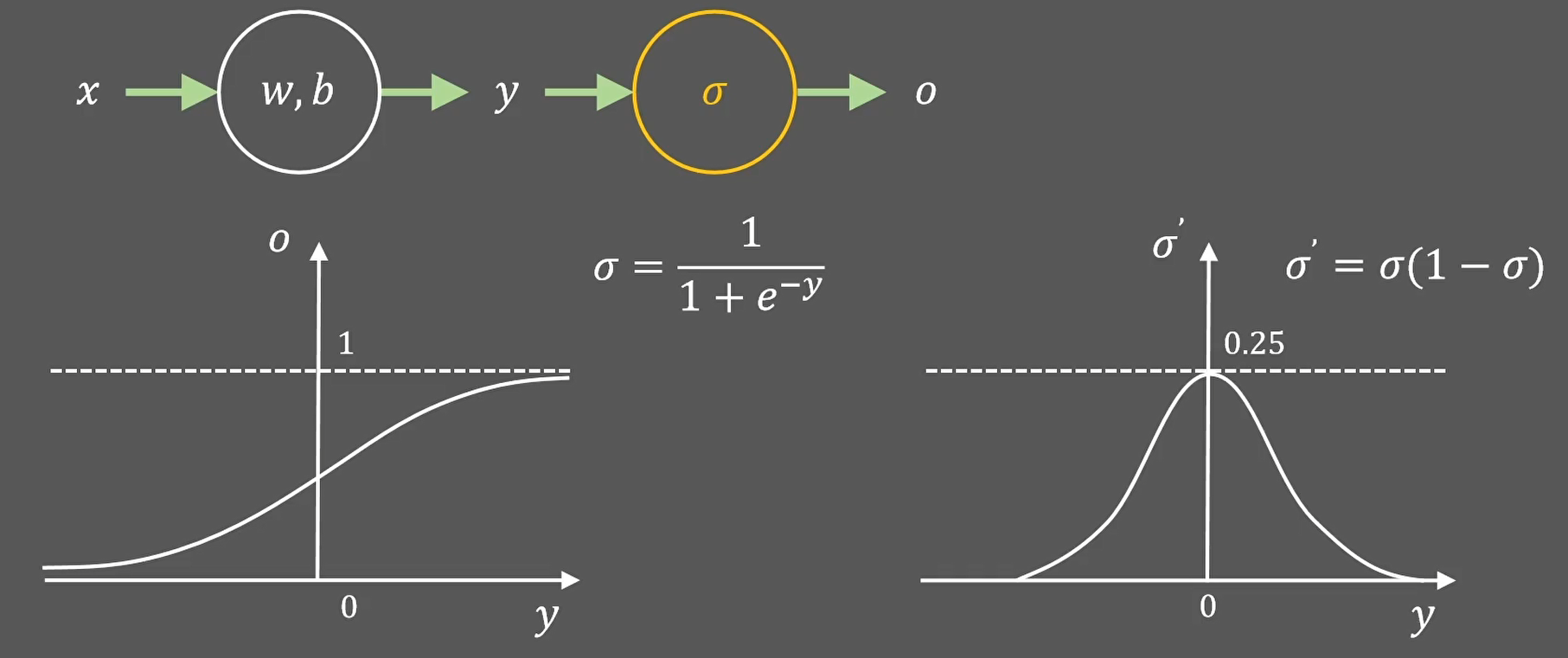
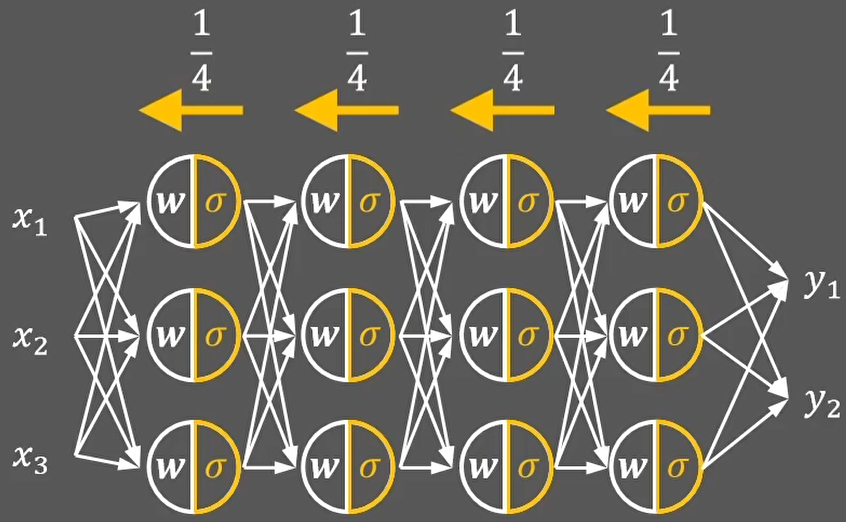
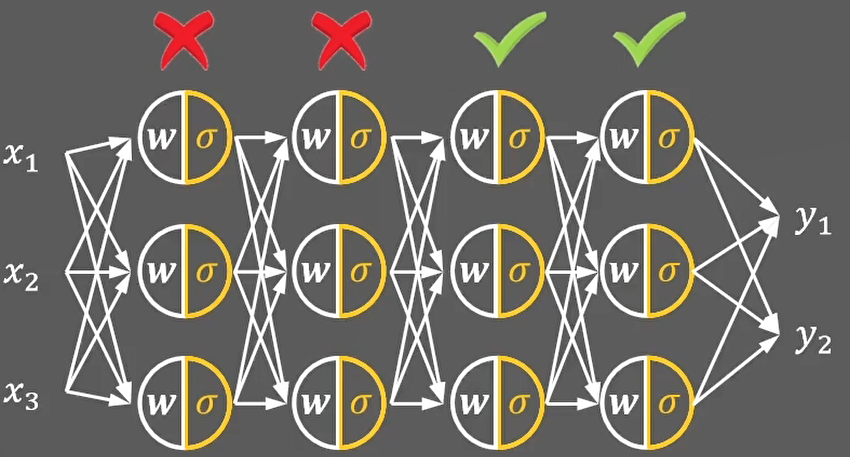
从上面的图可看出,sigmoid函数在输入值很大的时候,导数趋近于0,这一类函数也被称为饱和函数。 并且sigmoid的导数最大才是0.25,这就导致神经网络在反向传播时,如果网络深度比较大,最前面的层的导数几乎为0,导致参数(几乎)不被更新(因为参数的更新的幅度其实就是梯度值乘以学习率,梯度为0,参数更新也就停止了):
四层网络就等价于两层网络(参数不更新的情况下,该层的输出也就一直不变,相当于这些层没有作用):
这就是梯度消失现象。
- 缺点2:导致权值强制同向(同正同负),导致神经网络收敛缓慢
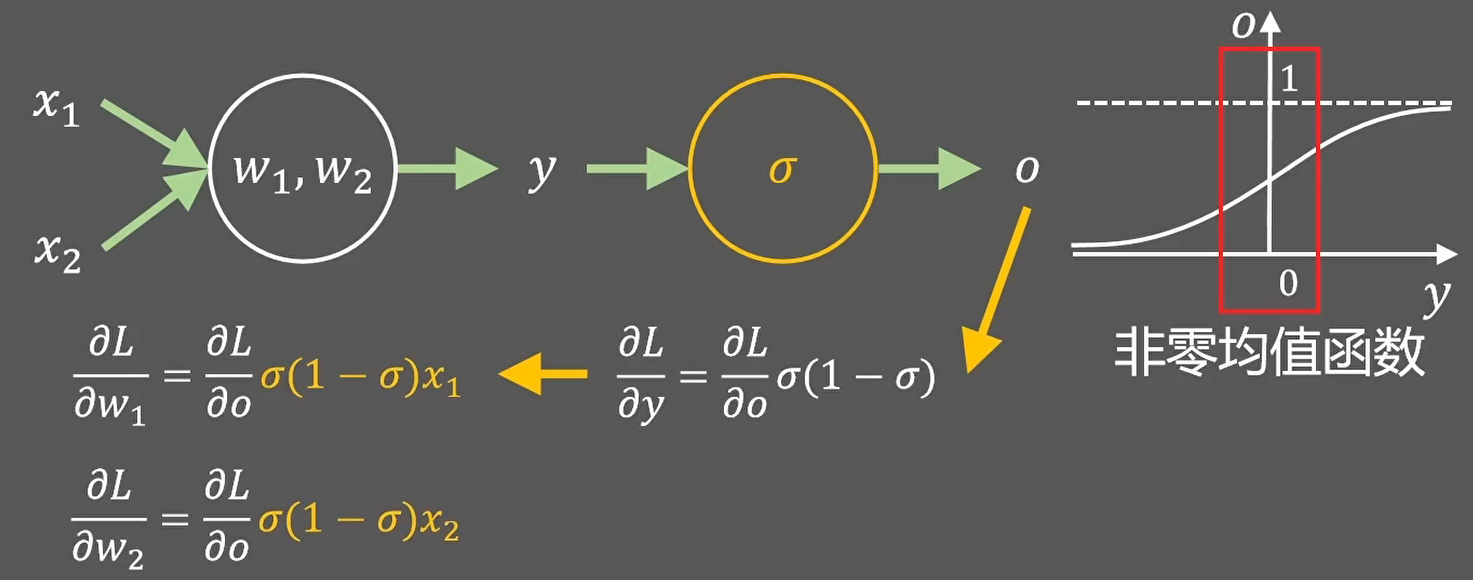
上面的w1和w2的梯度符号,始终一致,被强制的同时正向或者反向更新,导致神经网络更慢的收敛到预定位置。
- 代码示例:
import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(-10,10,1000)
y=tf.nn.sigmoid(x)
plt.plot(x,y)
plt.grid()
plt.show()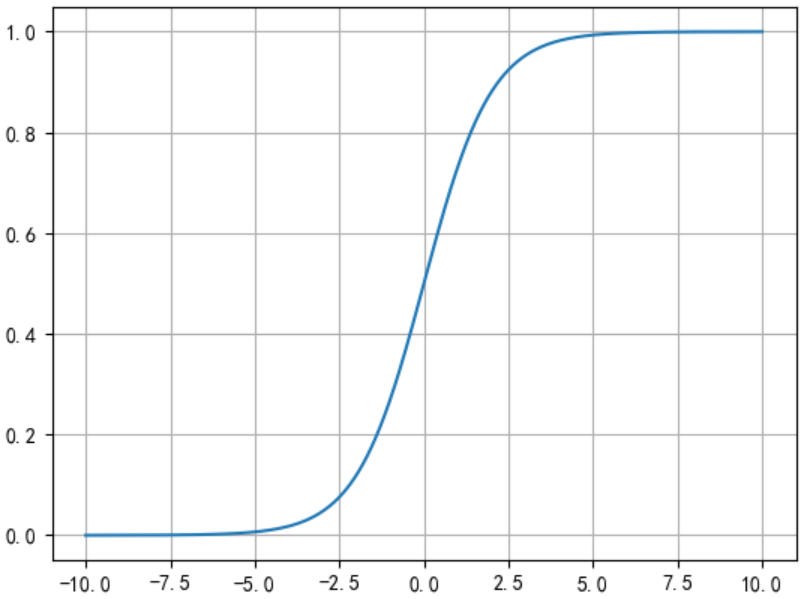
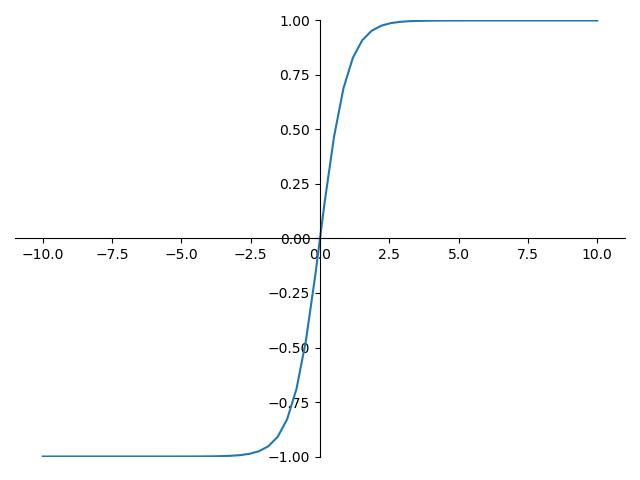
2. Tanh(双曲正切)
tanh也是一种非常常见的激活函数。与sigmoid相比,它是以0为中心的,使得其收敛速度要比sigmoid快,减少迭代次数。然而,从图中可以看出,tanh两侧的导数也为0,同样会造成梯度消失。
使用时可在隐藏层使用tanh函数,在输出层使用sigmoid函数。
- 公式:
-
特点:
- 中心对称(输出以0为中心),适合隐藏层。
- 梯度消失问题依然存在,但比Sigmoid稍好。
-
梯度公式:
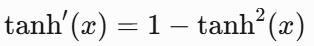
- 代码示例:
x=np.linspace(-10,10,1000)
y=tf.nn.tanh(x)
plt.plot(x,y)
plt.grid()
plt.show()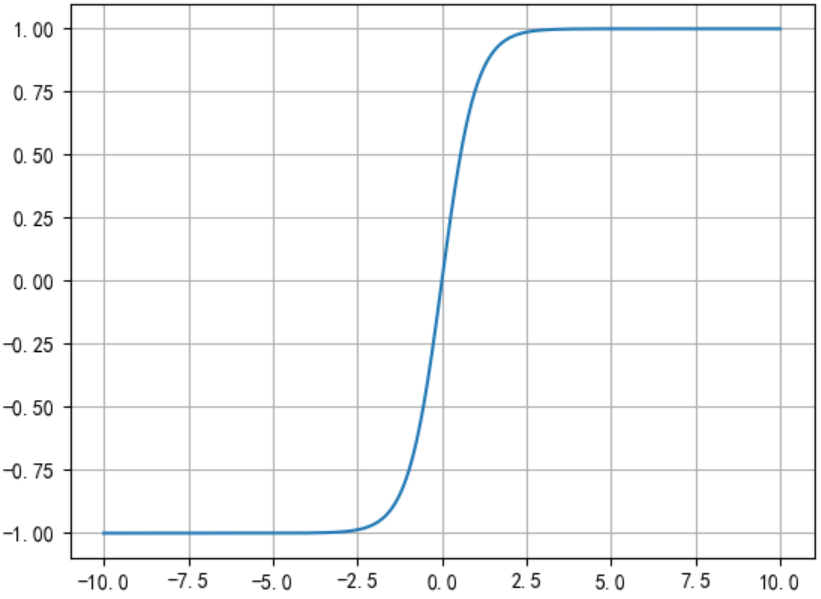
3. ReLU
(Rectified Linear Unit):修正线性单元
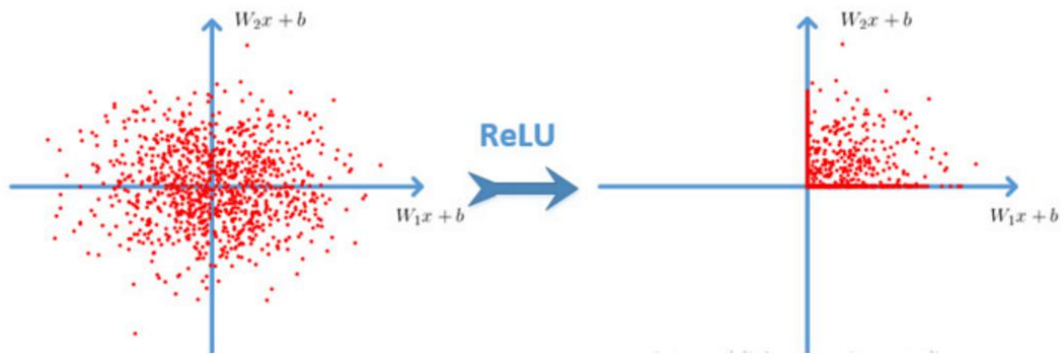
ReLU是目前最常用的激活函数。从图中可以看到,当x<0时,ReLU导数为0,而当x>0时,则不存在饱和问题。所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。然而,随着训练的推进,部分输入会落入小于0区域,导致对应权重无法更新。这种现象被称为“神经元死亡”。
与sigmoid相比,RELU的优势是:
-
- 采用sigmoid函数,计算量大(指数运算),反向传播求误差梯度时,求导涉及除法,计算量e相对大,而采用Relu激活函数,整个过程的计算量节省很多。
- sigmoid函数反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
- Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
-
公式:
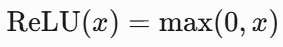
-
输出范围:[0, +∞)
-
梯度公式:
-
优点:
- 计算简单,加速收敛(梯度在正区间为1,避免梯度消失)。
-
公式简单实用
-
解决了梯度消失现象
-
计算速度更快
- 稀疏性
- 信息耦合程度低
表达维度尺寸可变
稀疏表达线性可分
保持特征的表达能力
- 信息耦合程度低
-
- 负数输入时梯度为0,神经元永久失效(杀死小于0的神经元)(可通过初始化或2013年提出的Leaky ReLU缓解)。
实现方法为:
x=np.linspace(-10,10,1000)
y=tf.nn.relu(x)
plt.plot(x,y)
plt.grid()
plt.show()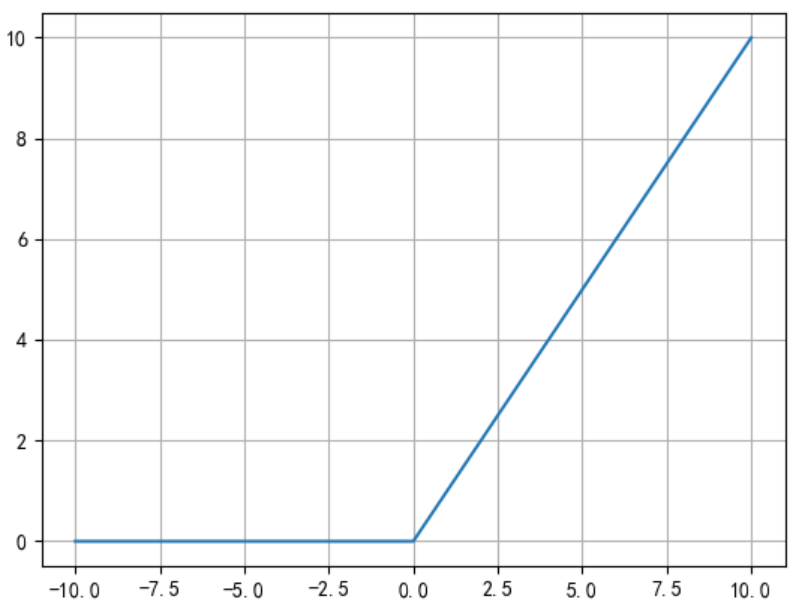
如果你对relu存在疑惑,或者不明白“分段线性函数”怎么就可以拟合任意非线性函数呢?可以参照文末:RELU原理详解
4. Leaky ReLU
Leaky ReLU是对ReLU的优化,解决了Relu会杀死一部分神经元的情况:
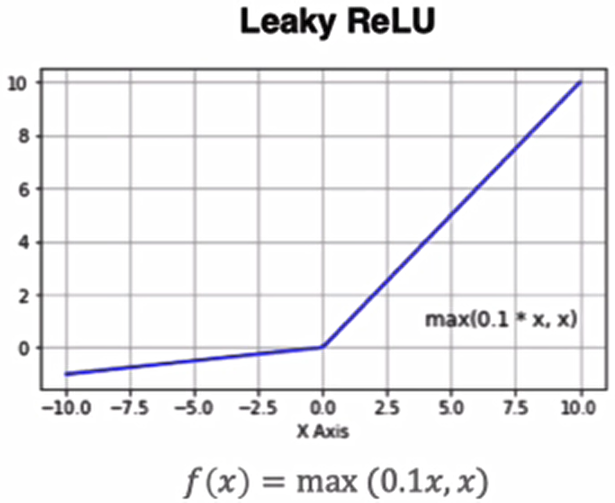
- 公式:

(通常 )
- 特点:
- 解决Dead ReLU问题,允许负区间有微小梯度。
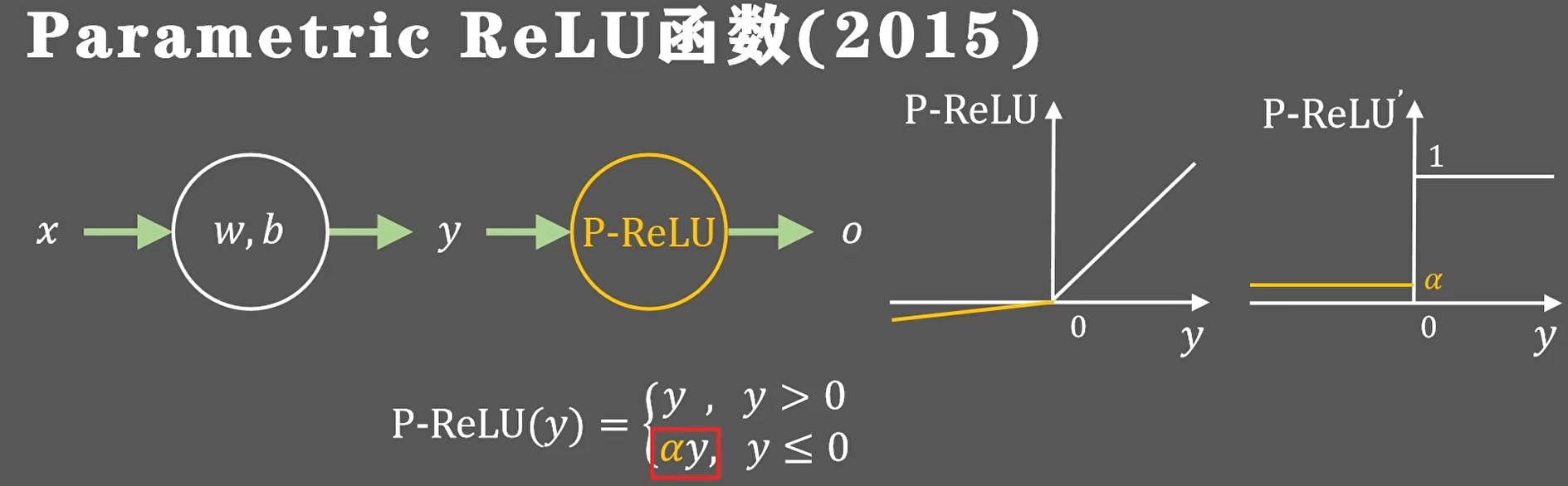
- 变种:Parametric ReLU(PReLU),将作为可学习参数。
- 代码示例:
x=np.linspace(-10,10,1000)
y=tf.nn.leaky_relu(x)
plt.plot(x,y)
plt.grid()
plt.show()
parametric relu
同样为了解决relu神经元坏死的问题,2015年提出了parametric relu激活函数,它将负半轴的梯度值更换成了可以动态学习调整的参数,是否保留稀疏性或者抑制神经元,都要通过训练过程来确定。
5. Softmax
softmax用于多分类的输出层中,它是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来。
- 公式:
softmax直白来说就是将网络输出的logits通过softmax函数,就映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们将它理解成概率,选取概率最大(也就是值对应最大的)节点,作为我们的预测目标类别。
- 输出范围:(0, 1),且和为1
- 特点:
- 用于多分类输出层,表示概率分布。
- 指数运算可能引发数值不稳定(实际实现时需做数值优化)。
- 代码示例:
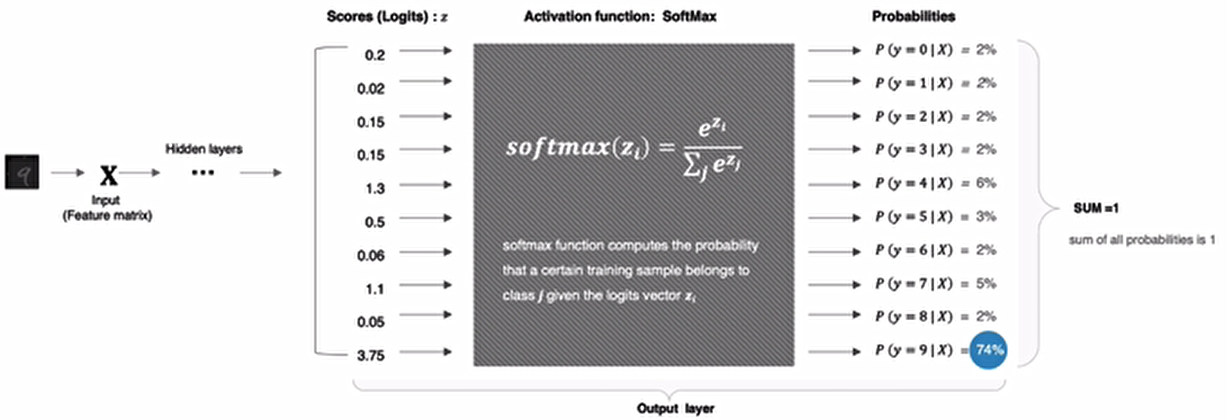
以上图中数字9的分类结果为例给大家进行演示:
# 数字对应的score
scores=tf.constant([0.2,0.02,0.15,1.3,0.5,0.06,1.1,0.05,3.75])
# 将其送入softmax计算分类结果
y=tf.nn.softmax(scores)
# 打印结果
print(y)tf.Tensor(
[0.02167152 0.01810157 0.02061459 0.06510484 0.02925349 0.01884031 0.05330333 0.01865285 0.7544575 ], shape=(9,), dtype=float32)其他激活函数
三、选择激活函数的指南
1. 隐藏层
- 首选ReLU:简单高效,缓解梯度消失,适合大多数情况。如果你使用了Relu,需要注意一下Dead Relu问题,避免出现大的梯度从而导致过多的神经元死亡。
- 尝试Leaky ReLU或ELU:如果模型存在Dead ReLU问题(如训练初期梯度更新缓慢)。
- 避免Sigmoid/Tanh:除非特殊需求(如压缩输出到特定范围)。(可以尝试使用tanh激活函数)
2. 输出层
- 回归任务:线性激活(无激活函数)。 线性激活即恒等映射 (Identity Function) 效果等同于
f(x) = x。 - 二分类:Sigmoid。
- 多分类:Softmax。
- 多标签分类:对每个输出用Sigmoid。
四、激活函数的数学意义
1. 非线性与模型能力
- 万能近似定理:一个包含足够多神经元的单隐藏层网络,配合非线性激活函数,可以逼近任意连续函数。
- 非线性激活函数使神经网络能够学习复杂模式(如图像、语言)。
2. 梯度传播分析
- Sigmoid/Tanh的导数在输入绝对值较大时趋近0,导致梯度消失。
- ReLU在正区间的导数为1,梯度直接传递,缓解梯度消失问题。
五、等价代码(Python)
import numpy as np
# Sigmoid
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# ReLU
def relu(x):
return np.maximum(0, x)
# Softmax(数值稳定实现)
def softmax(x):
x_exp = np.exp(x - np.max(x)) # 减去最大值防止溢出
return x_exp / np.sum(x_exp, axis=0)
# 示例
x = np.array([2.0, 1.0, 0.1])
print("Sigmoid:", sigmoid(x)) # 输出: [0.88, 0.73, 0.52]
print("ReLU:", relu(x)) # 输出: [2.0, 1.0, 0.0]
print("Softmax:", softmax(x)) # 输出: [0.66, 0.24, 0.10]六、常见问题解答
1. 为什么ReLU比Sigmoid更常用?
- 计算高效,梯度传播稳定,加速模型训练。
- Sigmoid易导致梯度消失,尤其在深层网络中。
2. 如何解决Dead ReLU问题?
- 使用Leaky ReLU或Parametric ReLU。
- 采用He初始化(初始化权重时考虑ReLU特性)。
3. 所有层都需要激活函数吗?
- 输出层可能不需要(如回归任务)。
- 隐藏层必须使用非线性激活函数(否则网络退化为线性模型)。
七、扩展:新型激活函数
Swish(Google提出):
![]()
-
- 比ReLU更平滑,实验表现更好。
GELU(高斯误差线性单元):
![]()
-
- 其中是标准正态分布的累积分布函数,被用于Transformer等模型。
八、总结
- 核心作用:引入非线性,控制输出范围,影响梯度传播。
- 推荐选择:隐藏层用ReLU或其变种,输出层根据任务选择。
- 避坑指南:避免Sigmoid/Tanh用于隐藏层,注意Dead ReLU问题。
理解激活函数是掌握神经网络设计的关键一步!如果遇到具体问题(如模型不收敛),可以优先检查激活函数的选择和初始化方法。
补充知识
RELU原理详解
你的疑问非常有洞察力!ReLU 的核心特性确实看似矛盾:它本身是分段线性的,在非负区间就是一个线性函数,但其在网络中的应用却能带来非线性表达能力。 这涉及对整体网络非线性和单层变换非线性的理解。让我们一步步解开这个矛盾:
关键点:非线性的来源是层间的堆叠与复合
-
单层 ReLU 是分段线性的,但整体网络是非线性的:
- 当你单独看一层用 ReLU 作为激活函数的线性变换(
Output = ReLU(W * X + b))时,在输入空间的不同区域:W * X + b >= 0的区域:输出Output = W * X + b(严格的线性函数)W * X + b < 0的区域:输出Output = 0(常数函数,是特殊的线性函数)
- 这一层本身确实是分段线性的(包括“死区”)。
- 但是,深度神经网络由许多层组成。当上一层的分段线性输出作为下一层线性变换的输入时,下一层的权重矩阵会作用在上一层的输出上。
- 当你单独看一层用 ReLU 作为激活函数的线性变换(
-
ReLU 的“拐点”引入非线性因素:
- ReLU 唯一的非线性来源于它的阈值操作,即在
z = W * X + b = 0这个点上发生突变(从 0 变到线性增长)。 - 这个分段的边界(由权重 W 和偏置 b 决定)本身带来了非线性。权重决定了边界的位置和方向(一个超平面),它将输入空间分成两个区域(激活区和死区)。边界本身(即
W * X + b = 0这条线/面)是一个非线性决策边界在输入空间上的投影。 - 堆叠效应: 想象网络第一层用权重矩阵
W1和偏置b1定义了一组分界线,将输入空间划分成多个“半空间”区域。每个区域里,第一层的输出是线性或常数。这些输出(虽然本身分段线性)作为第二层的输入X2。第二层权重W2和偏置b2又在X2空间定义一组新的分界线(新的超平面),把X2空间(即第一层的输出空间)划分为新的激活区和死区。由于X2本身是输入X的非线性函数(因为经过了第一层的非线性划分),第二层的分界线在原始输入空间X里就变成了更复杂的、非线性的曲线/曲面。 - 随着层数的增加,这些线性区域(由每个 ReLU 的激活/死区决定)相互组合、嵌套,使得网络能够拟合极其复杂的非线性边界。理论上讲,足够多使用 ReLU 的隐藏层可以以任意精度逼近任何连续函数。非线性来自层间权重的组合和 ReLU 阈值的划分作用。
- ReLU 唯一的非线性来源于它的阈值操作,即在
ReLU 的梯度与训练
-
x >= 0时梯度为常数1: 这实际上是一个巨大优势。梯度为常数1意味着梯度可以毫无衰减地(不像 Sigmoid/Tanh 会衰减)穿过激活层传递回之前的层。这显著缓解了早期 Sigmoid/Tanh 激活函数在深层网络中容易遇到的梯度消失问题(即梯度随着反向传播回前面的层时变得越来越小甚至消失,导致前面的层权重无法有效更新)。常数梯度(在激活区)保证了信息能更有效地流向浅层。 -
x < 0时梯度为0(神经元“死亡”问题): 这是 ReLU 的主要缺点。如果一个神经元的输入加权和(z = W * X + b)在训练过程中大部分时间都是负的(导致该 ReLU 单元输出始终为 0),那么它的梯度就始终为 0,因此它的权重在反向传播时得不到更新。这个神经元可能永远“死掉”,不再参与学习。改进版本(如 Leaky ReLU、Parametric ReLU、ELU)就是为了解决这个问题,在负半轴引入一个小的非零斜率(如y = 0.01x对于 Leaky ReLU),确保即使神经元初始落入死区,也仍有微小的梯度流回,有机会“复活”并参与学习。
对比 Sigmoid/Tanh
- Sigmoid 和 Tanh 在大部分区域(尤其是两端饱和区)的导数都 趋近于 0。这对于多层网络来说非常不利。
- 想象深度网络:在反向传播时,梯度需要逐层相乘(链式法则)。如果每经过一个 Sigmoid 层,梯度就被乘以一个小于 1 的数(导数),层数一多,前面的层梯度就几乎变成零了,导致训练停滞(梯度消失)。
- ReLU 在正区将导数“固定”为 1,避开了这个乘法衰减陷阱(至少对于那些激活的神经元路径来说)。虽然负区导数为零也有问题(神经元死亡),但这通常不如梯度消失对深度训练的阻碍那么大。
结论:合理性的核心
- ReLU 提供的是划分非线性的潜力(通过其阈值操作),并依赖多层堆叠和权重学习来实现复杂的整体非线性函数。 单层或局部的“线性”性质被全局的组合覆盖。
- ReLU 梯度性质的设计(正区导数为 1)是为了解决训练深层网络的核心难题——梯度消失问题,这是神经网络能够训练至收敛的关键。 与训练效率和模型深度相比,局部的“非理想非线性”是一个可以接受的权衡,并且通过层堆叠得到了完美解决。
所以,这并非“不合理”,而是一种聪明的设计权衡:
- 代价: 输出分段线性(靠堆叠解决)、负半轴梯度为 0(改进变种缓解)。
- 收益: 简单、计算高效、正半轴无梯度衰减(解决深层训练瓶颈)、引入划分非线性的能力。
理解 ReLU “简单外表下(分段线性)如何通过组合产生强大非线性能力(全局)”是理解现代深度学习架构的关键一步。你的质疑恰恰触达了深度神经网络非线性的核心原理!

1. 无上界特性(Unbounded Output)
- 数学表达:
→ 当 时函数值无上限 - 实例:
假设某神经元输入 = 100,权重 → 输出 = 150 → 下一层输出 = 225 → 指数级增长
2. 梯度累积机制(关键难点)
- 前向传播:激活值持续增大
- 反向传播:梯度链式求导引发指数放大

3. ReLU的特殊性:导数恒为1的放大器
| 层数 | 梯度计算 | 累乘效果 |
|---|---|---|
| 第n层 | 梯度×1 | |
| 第n-1层 | 梯度×1×1 | |
| ... | ... | ... |
| k层后 | 无衰减! |
对比Sigmoid:
→ k层后梯度≈ → 指数衰减
二、循环网络(RNN)的灾难性场景
设时间步 的隐藏状态 ![]()
梯度沿时间反向传播:
∂L/∂W ∝ [∂h_T/∂h_{T-1}] · [∂h_{T-1}/∂h_{T-2}] · ... · [∂h_1/∂W]
↑ ↑ ↑
ReLU导数=1 ReLU导数=1 ReLU导数=1符号“∝”表示两者间的比例关系,主要用于正比例。具体来说,当说“y∝x”时,意味着物理量y与物理量x成正比关系,即y的变化与x的变化是同步的,比例常数可以是任意实数。
- 当 时,梯度累积 → 梯度毫无衰减
- 若权重矩阵 的特征值 → 梯度
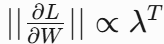 → 指数爆炸
→ 指数爆炸 - 浮点数溢出:当 时, > float32上限(3.4e38)
解决方案
-
参数初始化:
-
使用Xavier/Glorot初始化
-
或He初始化(抑制初始激活值,专为ReLU设计)
-
确保初始输出保持在合理范围
- 网络结构改进:
-
-
梯度裁剪:强制限制梯度最大值
-
optimizer = tf.keras.optimizers.Adam(clipvalue=1.0)-
- 批归一化(BatchNorm):标准化每层输入,控制激活值范围
| 方法 | 公式 | 效果 |
|---|---|---|
| BatchNorm | 约束每层输出分布 | |
| LayerNorm | 适用RNN/Transformer |
model.add(tf.keras.layers.BatchNormalization())-
- 残差连接:提供梯度直通路径
x = Conv2D(64, 3)(input)
x = BatchNormalization()(x)
x = ReLU()(x)
output = Add()([input, x]) # 残差连接-
- 权重正则化:惩罚大权重值
model.add(Dense(64, kernel_regularizer=l2(0.01)))为何其他激活函数无此问题
-
Sigmoid/Tanh:
-
输出有界(Sigmoid:0-1, Tanh:-1-1)
-
梯度最大0.25,不易爆炸
-
-
Leaky ReLU:
-
负区间有小的斜率,缓解神经元"死亡"问题
-
但仍无上界,可能梯度爆炸
-
-
Swish/Mish:
-
自门控机制,平滑过渡
-
理论上仍可能爆炸,但概率较低
-
实际应用建议
当使用ReLU时,必须配合以下至少一项:
-
合理的权重初始化
-
批归一化层
-
梯度裁剪
-
残差连接结构
特别是在循环神经网络(RNN/LSTM)中,梯度爆炸风险更高,通常需要:
# LSTM+梯度裁剪的典型实现
model = Sequential([
LSTM(128, return_sequences=True,
kernel_initializer='he_normal'),
BatchNormalization(),
LSTM(128, kernel_initializer='he_normal'),
Dense(10)
])
optimizer = Adam(clipnorm=1.0) # 梯度裁剪理解这个机制对调试神经网络至关重要——当训练出现NaN损失时,首先应该检查梯度爆炸问题!
遇到梯度爆炸时,优先检查:
- 网络深度/时间步是否过长
- 是否使用了He初始化
- ReLU后是否添加了归一化层


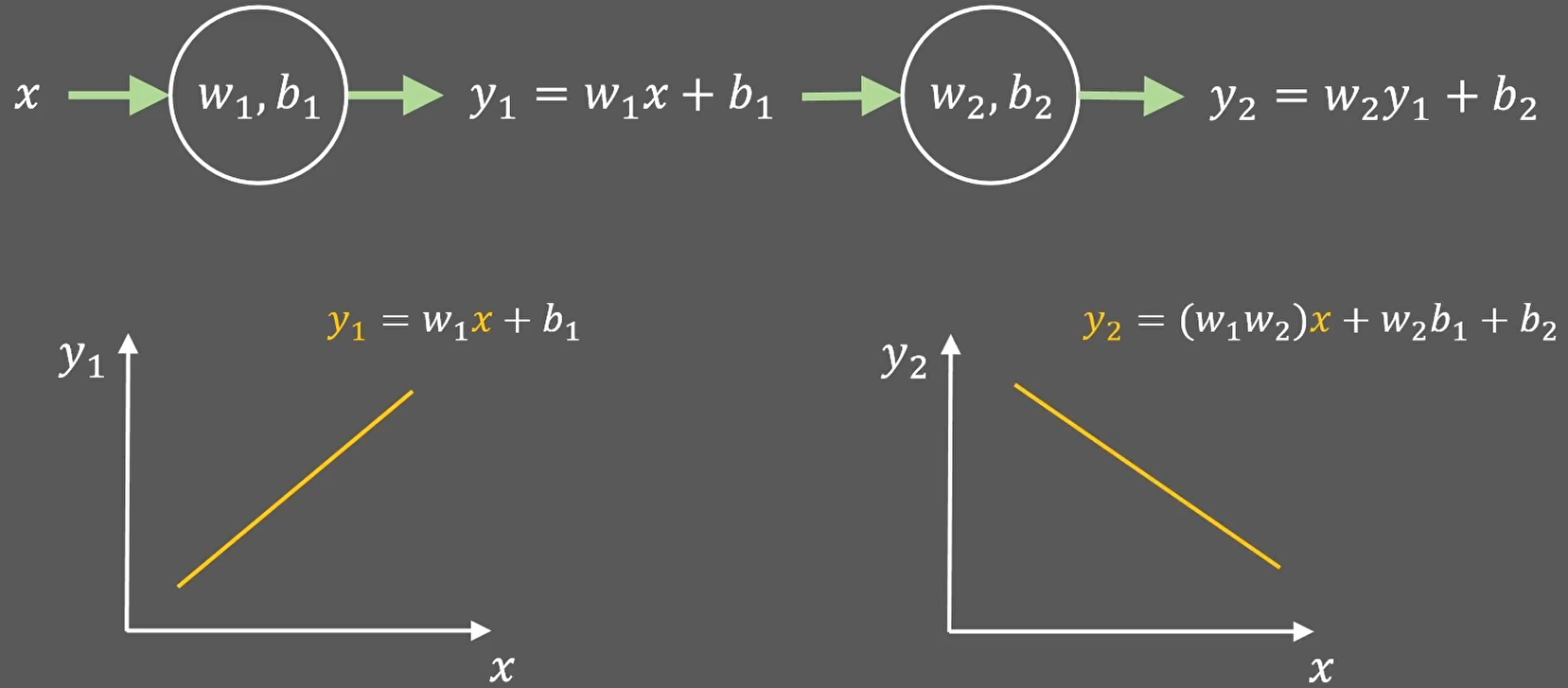

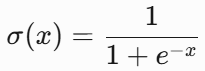
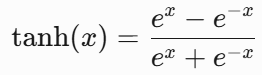

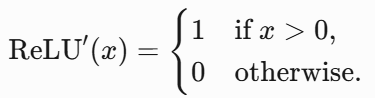
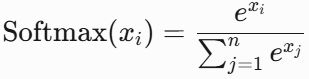
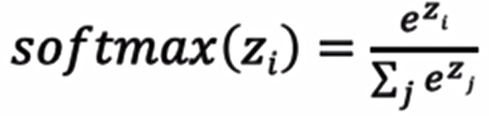


 浙公网安备 33010602011771号
浙公网安备 33010602011771号