会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
锦依卫Lijilai
华风夏韵,洛水天依
首页
新随笔
联系
管理
2020年7月28日
2018-2020全国卷Ⅱ数学考点整理
摘要: 2020全国卷Ⅱ 1.集合的关系及运算 2.任意角的三角函数 3.概率 4.等差数列求和 5.直线与圆的方程 6.特殊数列 7.三视图 8.双曲线 9.函数的单调性与奇偶性 10.球的性质 11.函数的单调性 12.信息题 13.平面向量运算 14.排列组合 15.复数的运算 16.立体几何、命题
阅读全文
posted @ 2020-07-28 09:13 锦依卫Lijilai
阅读(448)
评论(0)
推荐(0)
2020年7月24日
高中物理知识点1.0版
摘要: 链接: https://pan.baidu.com/s/1GDw3NewCrU1LA9Vie4ecyw 提取码: 8yn3
阅读全文
posted @ 2020-07-24 17:00 锦依卫Lijilai
阅读(211)
评论(1)
推荐(0)
2020年6月23日
高考数学一轮复习知识网络(持续更新)
摘要: 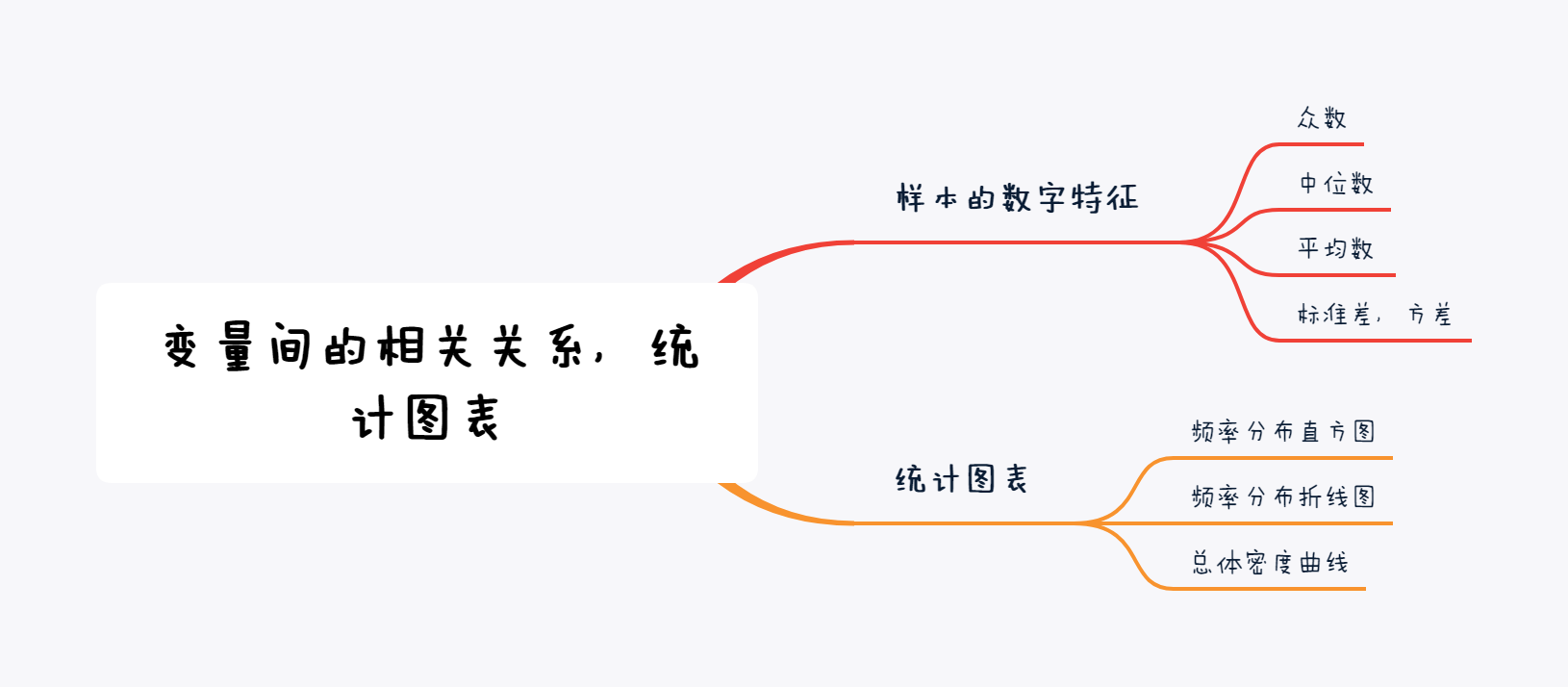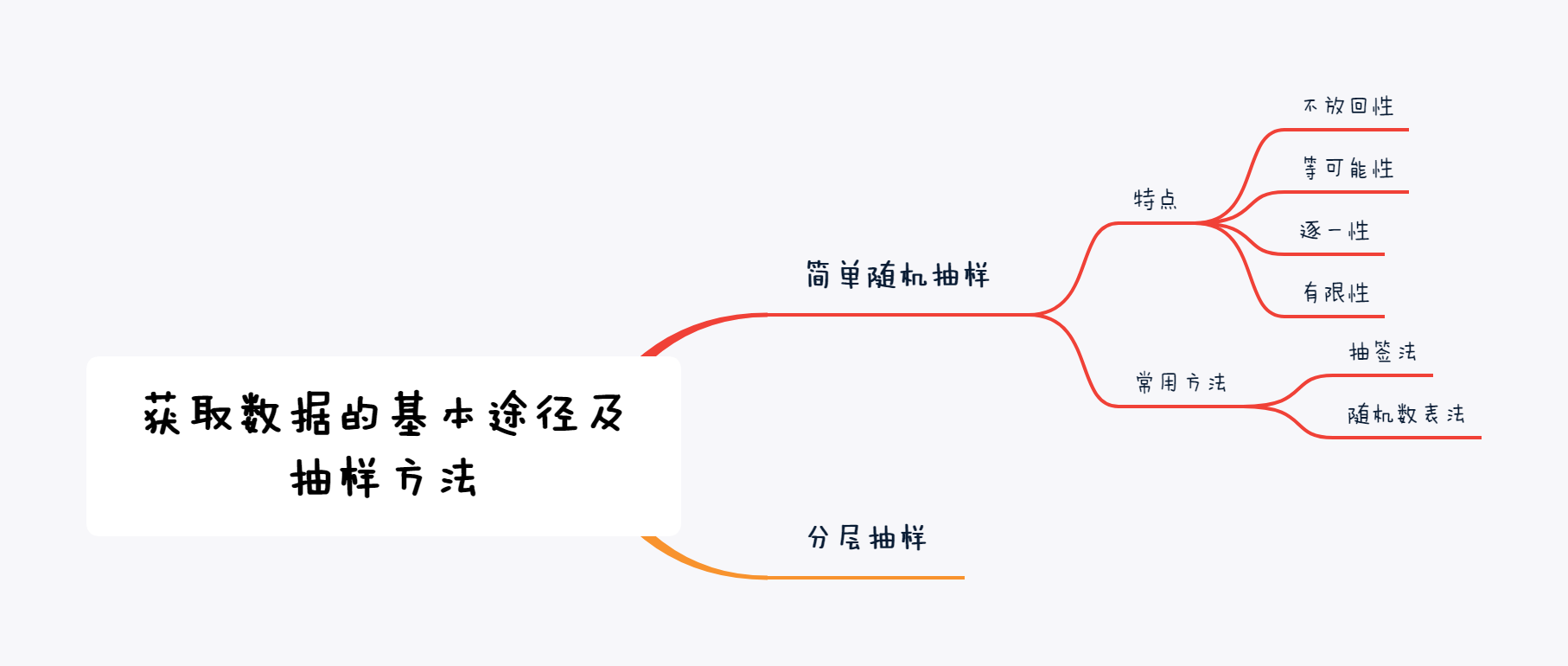
评论(0)
推荐(1)
2020年6月21日
退役记
摘要: 拖延了3个月终于退役了 既然退役了还是要按照传统写写感想。 第一次接触OI是19年9月吧,当时对OI一无所知hhhhh,主要是被教练钢哥(gg)在高一第一节信息课一顿安利,然后还发现我确实具有这方面的天赋,于是就去了。然后一步步见证了学OI的人数从70+到20+。。。 其实整个高一上学期就只是学了语
阅读全文
posted @ 2020-06-21 21:42 锦依卫Lijilai
阅读(307)
评论(1)
推荐(0)
2020年4月23日
POJ杂题题解
摘要: POJ1147 根据最后一列,可以确定答案中0/1的个数,同样第一列也确定了,因为每次操作之后得到的矩阵都是排过序的,不妨考虑一下把最后一列移到第一列,这样可以得到最后一列与第一列排序的对应关系,然后根据这个对应关系就可以知道每一行经过排序会发生什么变化,这样不断递推就可以求出整个矩阵了。由于只需要
阅读全文
posted @ 2020-04-23 16:15 锦依卫Lijilai
阅读(248)
评论(0)
推荐(0)
2020年4月22日
几何公式
摘要: 【三角形】: 1. 半周长 $p=\frac{a+b+c}{2}$ 2. 面积 $S=\frac{ah}{2}=\frac{ab\sin C}{2}=\sqrt{p(p a)(p b)(p c)}$ 3. 中线 $M_a=\frac{\sqrt{2b^2+2c^2 a^2}}{2}=\frac{\s
阅读全文
posted @ 2020-04-22 16:17 锦依卫Lijilai
阅读(736)
评论(0)
推荐(0)
2020年4月15日
FFT学习笔记
摘要: FFT学习笔记 FFT,快速傅里叶变换,是一种在$O(n\log n)$的时间内计算两个多项式乘积的算法。 前置芝士 复数 没学过的请自行翻阅高中数学选修2 2。 多项式的表示 给出一个多项式 $f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n $ 系数表示法 就是
阅读全文
posted @ 2020-04-15 21:07 锦依卫Lijilai
阅读(253)
评论(0)
推荐(0)
2020年4月4日
[SDOI2019] 快速查询
摘要: 首先,这是一道省选可以切的题(虽然我其实一开始并不会)。 分析6个操作,不难发现其实所有的操作要么是单点修改/查询,要么是整个序列的修改/查询。而众所周知,只对整个序列进行操作有些优美的性质。 首先我们维护3个标记,$add$,$mul$,$sum$,分别是加法标记,乘法标记,以及整个序列的和。类似
阅读全文
posted @ 2020-04-04 19:45 锦依卫Lijilai
阅读(156)
评论(0)
推荐(0)
2020年4月2日
[计蒜客 A1998]Ka Chang
摘要: 题意:给一棵根为1号结点的树,每个点有权值,初始是0,$Q$ 次操作,每次: 1. 对深度为 $L$ 的点全部加权值 $x$(根结点深度为0) 2. 输出子树权值和 $n,Q \leq 10^5$ 先考虑操作2,显然这是个树上子树统计问题,dfs序+线段树/树状数组就可以在$O(\log n)$复杂
阅读全文
posted @ 2020-04-02 18:53 锦依卫Lijilai
阅读(152)
评论(0)
推荐(0)
2020年3月17日
[Luogu P4318]完全平方数
摘要: 要求第$k$个不是完全平方数的正整数倍的数,直接求显然十分暴力,于是考虑一下二分答案。 二分之后,问题转化为求$[1,mid]$这段区间内有多少个无完全平方因子的整数。 先考虑一下完全平方数对答案的贡献,$2^2$可以对其所有的倍数产生贡献,$3^2$可以对其所有的倍数产生贡献,但是我们发现$6^2
阅读全文
posted @ 2020-03-17 08:10 锦依卫Lijilai
阅读(171)
评论(0)
推荐(0)
下一页
公告