几何公式

【三角形】:

1. 半周长 \(p=\frac{a+b+c}{2}\)

2. 面积 \(S=\frac{ah}{2}=\frac{ab\sin C}{2}=\sqrt{p(p-a)(p-b)(p-c)}\)

3. 中线 \(M_a=\frac{\sqrt{2b^2+2c^2-a^2}}{2}=\frac{\sqrt{b^2+c^2+2bc\cos A}}{2}\)

4. 角平分线 \(T_a=\frac{\sqrt{bc((b+c)^2-a^2)}}{b+c}=\frac{2bc\cos\frac{A}{2}}{b+c}\)

5. 高线 \(H_a=b\sin C=c\sin B=\sqrt{b^2-(\frac{a^2+b^2-c^2}{2a})^2}\)

6. 内切圆半径 \(r=\frac{S}{p}=\frac{a\sin \frac{B}{2}\sin \frac{C}{2}}{\sin \frac{B+C}{2}}=4R\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}=\frac{ab\sin C}{2}=\frac{\sqrt{p(p-a)(p-b)(p-c)}}{p}=p\tan \frac{A}{2}\tan \frac{B}{2}\tan \frac{C}{2}\)

7. 外接圆半径 \(R=\frac{abc}{4S}=\frac{a}{2\sin A}=\frac{b}{2\sin B}=\frac{c}{2\sin C}\)

【四边形】:

\(D_1\) , \(D_2\) 为对角线, \(M\)对角线中点连线, \(A\)为对角线夹角

1. \(a^2+b^2+c^2+d^2=D_1^2+D_2^2+4M^2\)

2. \(S=\frac{D_1D_2\sin A}{2}\)

(以下对圆的内接四边形)

3. \(ac+bd=D_1D_2\)

4. \(S=\sqrt{(p-a)(p-b)(p-c)(p-d)}\), \(p\)为半周长

【正 \(n\) 边形】:

\(R\) 为外接圆半径, \(r\) 为内切圆半径

1. 中心角 \(A=\frac{2\pi}{n}\)

2. 内角 \(C=\frac{(n-2)\pi}{n}\)

3. 边长 \(a=2\sqrt{R^2-r^2}=2R\sin \frac{A}{2}=2r\tan \frac{A}{2}\)

4. 面积\(S=\frac{nar}2=nr^2 \tan \frac{A}2=\frac{nR^2\sin A}2=\frac{na^2}{4\tan \frac{A}2}\)

【圆】:

1. 弧长 \(L=rA\)

2. 弦长 \(a=2\sqrt{2hr-h^2}=2r\sin\frac{A}2\)

3. 弓形高 \(h=r-\sqrt{\frac{r^2-a^2}4}=r(1-\cos\frac{A}2)=\frac{a\tan \frac{A}4}2\)

4. 扇形面积 \(S_1=\frac{rl}2=\frac{r^2A}2\)

5. 弓形面积 \(S_2=\frac{rl-a(r-h)}2=r^2\frac{A-\sin A}2\)

【棱柱】:

1. 体积 \(V=Ah\), \(A\) 为底面积,\(h\) 为高

2. 侧面积 \(S=lp\), \(l\) 为棱长, \(p\) 为直截面周长

3. 全面积 \(T=S+2A\)

【棱锥】:

1. 体积 \(V=\frac{Ah}3\),\(A\) 为底面积,\(h\) 为高

(以下对正棱锥)

2. 侧面积 \(S=\frac{lp}2\), \(l\) 为斜高, \(p\) 为底面周长

3. 全面积 \(T=S+A\)

【棱台】:

1. 体积 \(V=\frac{(A_1+A_2+\sqrt{A_1A_2})h}3\),\(A_1,A_2\) 为上下底面积,\(h\) 为高

(以下为正棱台)

2. 侧面积 \(S=\frac{(p_1+p_2)l}2\),\(p_1,p_2\)为上下底面周长,\(l\) 为斜高

3. 全面积 \(T=S+A_1+A_2\)

【圆柱】:

1. 侧面积 \(S=2\pi rh\)

2. 全面积 \(T=2\pi r(h+r)\)

3. 体积 \(V=\pi r^2h\)

【圆锥】:

1. 母线 \(l=\sqrt{h^2+r^2}\)

2. 侧面积 \(S=\pi rl\)

3. 全面积 \(T=\pi r(l+r)\)

4. 体积 \(V=\frac{\pi r^2h}3\)

【圆台】:

1. 母线 \(l=\sqrt{h^2+(r_1-r_2)^2}\)

2. 侧面积 \(S=\pi(r_1+r_2)l\)

3. 全面积 \(T=\pi r_1(L+r_1)+\pi r_2(L+r_2)\)

4. 体积 \(V=\frac{\pi(r_1^2+r_2^2+r_1r_2)h}3\)

【球】:

1. 全面积 \(T=4\pi r^2\)

2. 体积 \(V=\frac{4}{3}\pi r^3\)

【球台】:

1. 侧面积 \(S=2\pi r h\)

2. 全面积 \(T=\pi(2rh+r_1^2+r_2^2)\)

3. 体积 \(V=\frac{\pi h(3(r_1^2+r_2^2)+h^2)}6\)

【球扇形】:

1. 全面积 \(T=\pi r(2h+r_0)\), \(h\) 为球冠高, \(r_0\)为球冠底面半径

2. 体积 \(V=\frac{2}{3}\pi r^2h\)
   
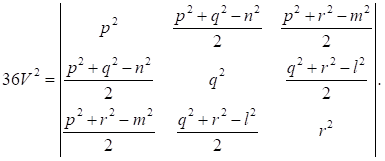
   Euler的任意四面体体积公式（已知边长求体积）
   

已知4点坐标求体积（其中四个点的坐标分别为\(（x_1,y_1,z_1）,（x_2,y_2,z_2）,（x_3,y_3,z_3）,（x_4,y_4,z_4）\)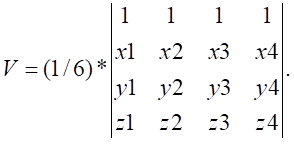

注意事项：

1. 注意舍入方式(\(0.5\) 的舍入方向);防止输出 \(-0\).

2. 几何题注意多测试不对称数据.

3. 整数几何注意xmult和dmult是否会出界;

符点几何注意eps的使用.

4. 避免使用斜率;注意除数是否会为 \(0\).

5. 公式一定要化简后再代入.

6. 判断同一个\(2\pi\) 域内两角度差应该是

\(abs(a_1-a_2)<\beta\ ||\ abs(a_1-a_2)>2\pi-\beta\);

相等应该是

\(abs(a_1-a_2)<eps\ ||\ abs(a_1-a_2)>2\pi-eps\)

7. 需要的话尽量使用atan2,注意:\(atan2(0,0)=0,atan2(1,0)=\frac{\pi}2,atan2(-1,0)=-\frac{\pi}2,atan2(0,1)=0,atan2(0,-1)=\pi\).

8. 叉积cross product \(= |\vec u|\times |\vec v| \times sin<\vec u,\vec v>\)

点积dot product \(= |\vec u|\times |\vec v| \times cos<\vec u,\vec v>\)

9. \((P_1-P_0)\times (P_2-P_0)\)结果的意义:

正: \((P_0,P_1)\) 在 \((P_0,P_2)\) 顺时针 \((0,\pi)\)内

负: \((P_0,P_1)\) 在 \((P_0,P_2)\) 逆时针\((0,\pi)\)内

0 : \((P_0,P_1)\) \((P_0,P_2)\) 共线,夹角为 \(0\) 或 \(\pi\)