回滚莫队
起因是学校老师不知道抽什么风,在比赛里(约 S 级)放了一道回滚莫队。作为一个只了解过基础莫队的蒟蒻,本蒟只好自学了一下回滚莫队。
回顾旧知
引入
你会发现,普通莫队中,我们对于扩展的要求比较高,要求我们可加可减。
但是,考虑一个问题,如果一个题加好写而减不好写(或减好写而加不好写),那我们还可以使用莫队吗?
P5906 【模板】回滚莫队&不删除莫队
我们发现,作为这道题,扩展还算可以,退位由于你不知道次大,所以最大死去后你需要重找,因此普通莫队不好写。(或者你可以i在扩展的时候加上什么神奇的线段树。)
由此引入:回滚莫队。
NEW:回滚莫队
当你发现莫队的扩展难写时,不妨想一想这种算法!
思想:
我们把我们的块分成两类:块内的和块际的(国内国际)。
设块长为 \(B\)。
块内的询问,我们直接处理回答即可,为 \(\mathcal O(B)\)。
块外的,为了减少我们删除的次数,我们将其按照左端点所在块分类(实际上如果你按莫队排序,那一类一定连在一起)。
对于一类的,我们将他以块的断点断开。当然,你也可以看成是我们把询问拆开为左右两个部分。
对于右边的部分,它的左端点一定都是分开的断点,而我们由于按端点从小到大排序了,所以这部分和原先普通莫队的扩展是同一个道理(在每一次询问时通过莫队扩展移至询问的右端点)。
对于左边这一部分,它相对无序,每次询问时直接向左做一个普通莫队扩展。
但由于会对当前原先就在右侧的莫对产生影响,所以我们要在每次左侧更新后恢复。
图解
过程见下四图:
(一)同一类需要处理的询问(左端点为同一块,按右端点从小到大排序):1、2、3。
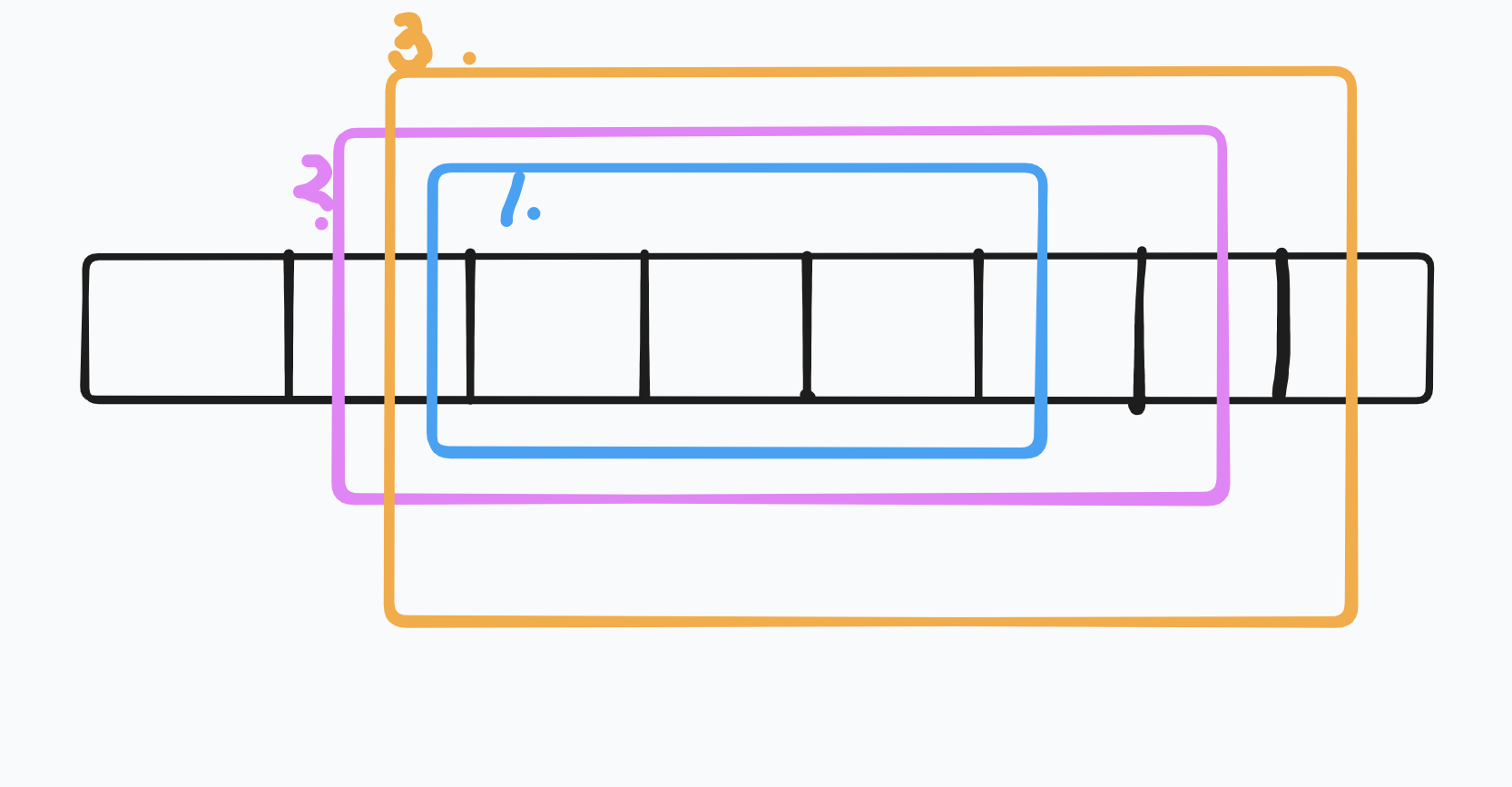
(二)先处理 1 询问。以断点 \(L\) 分开。分为左红和右绿两部分,右面直接让 \(r\) 扩展到达,左面用 \(l\) 去做,得到答案后将左红恢复。
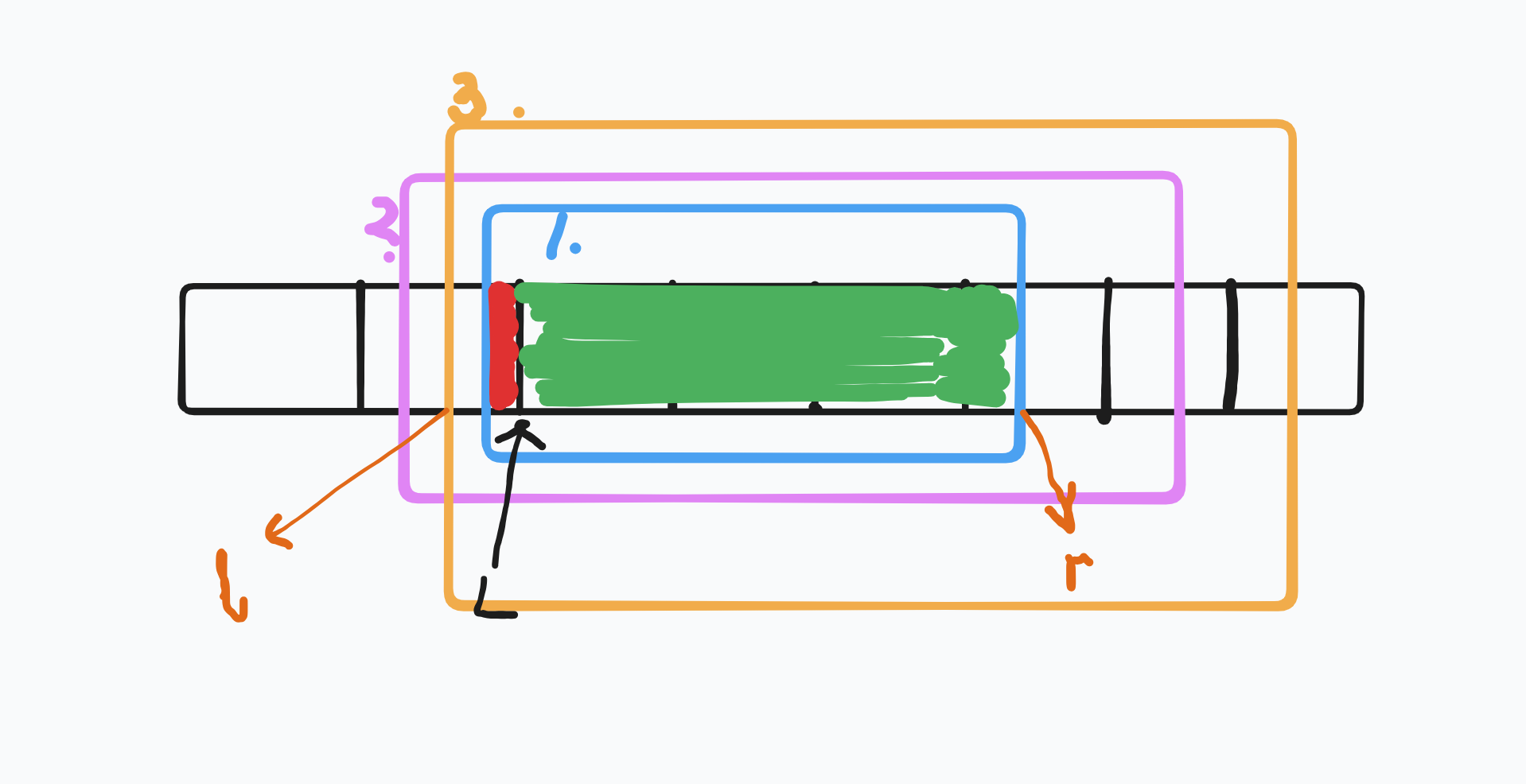
(三)处理 2 询问。右端点 \(r\) 直接由上一次的 \(r\) 向右拓展得到。左端点 \(l\) 依旧是从 \(L\) 从头扩展得到。
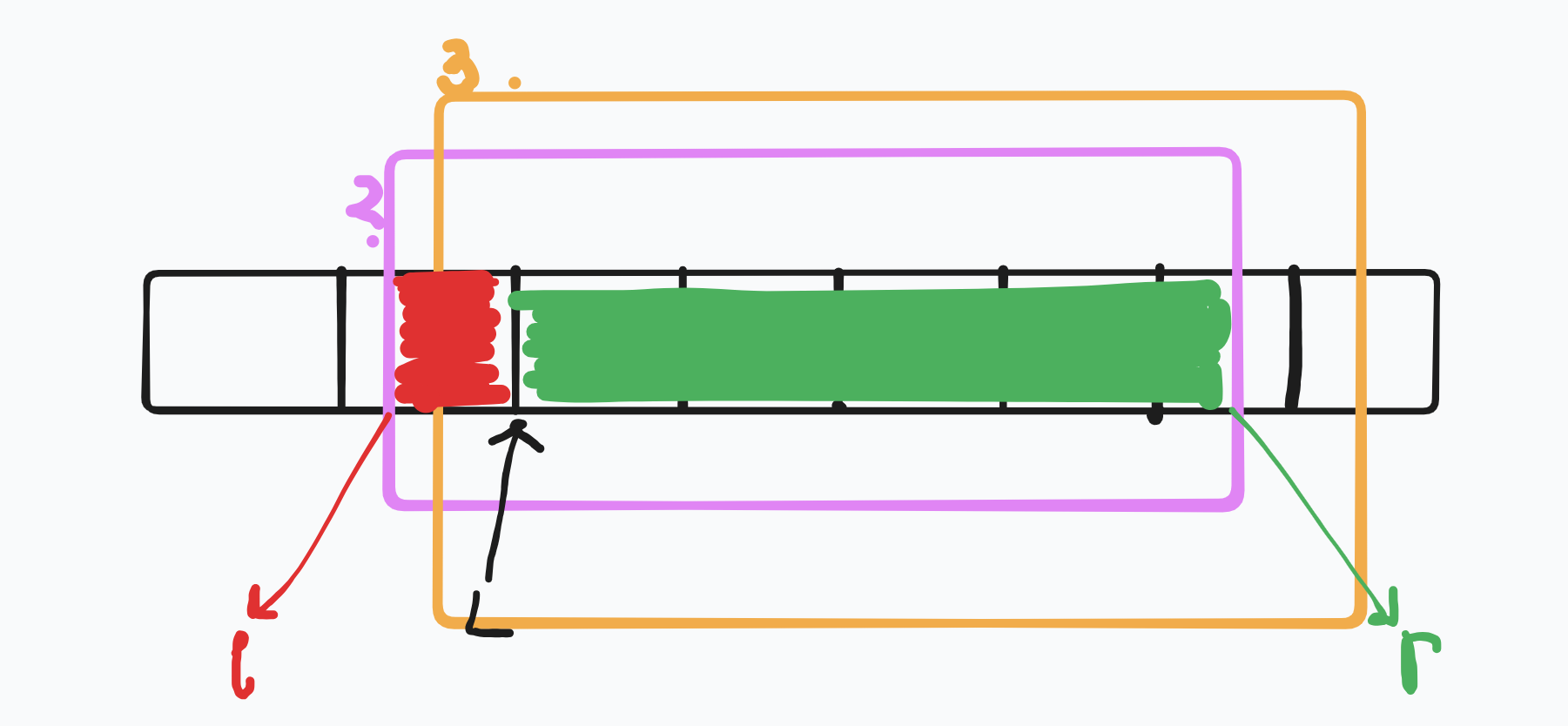
(四)处理 3 询问。\(r\) 右移拓展,\(l\) 重新计算。
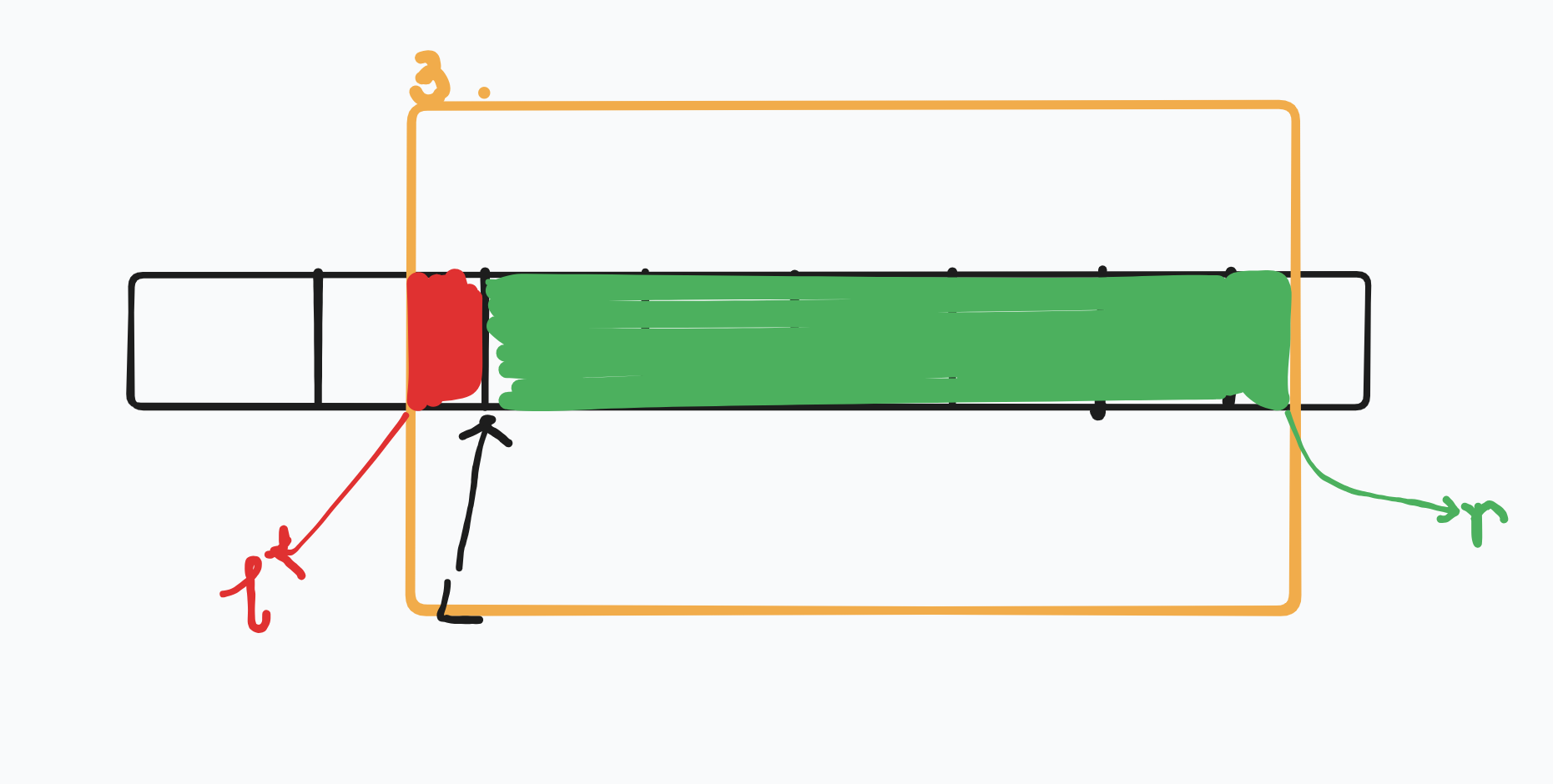
扩展
现在我们的主要矛盾就已经转为纯扩展怎么做。当然你可以用一些类似并查集、线段树的妙妙做法。
但他们都会带上一个 \(\log n\) 的复杂度。
这里我们讲一种 \(O(1)\) 的转移。
我们定义两个值域数组 \(h\) 和 \(t\),分别表示当前区间内 \(x\) 这个数第一次和最后一次出现的下标。
然后直接和当前答案取最大就可以了。
代码实现
#include <bits/stdc++.h>
using namespace std;
#define get(x) ((x-1)/S+1)
#define get_l(x) ((x-1)*S+1)
#define get_r(x) min(n, x*S) // 本人分块喜欢用宏定义
int n, m, S, M, cnt, kkk;
int a[200010], ans[200010], h[200010], t[200010];
struct Node { int id, l, r; } q[200010]; // 询问
pair<int, int> b[200010]; // 离散化的
stack<pair<int, pair<int, int> > > stk; // 复原用的栈
bool cmp(const Node& a, const Node& b) { return get(a.l) == get(b.l) ? a.r < b.r : get(a.l) < get(b.l); } // 莫队排序
void add(int j){ // 普通向右拓展的加法
if(!h[a[j]]) h[a[j]] = j;
t[a[j]] = j;
cnt = max(cnt, - h[a[j]] + t[a[j]]);
}
void add1(int j){ // l 单独向左做的扩展
stk.push({a[j], {t[a[j]], h[a[j]]}});
if(!t[a[j]]) t[a[j]] = j;
h[a[j]] = j;
kkk = max(kkk, - h[a[j]] + t[a[j]]);
}
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin>>n;
S = sqrt(n);
for (int i = 1; i <= n; i ++) cin >> a[i], b[i].first = a[i], b[i].second = i;
sort(b + 1, b + n + 1);
cin>>m;
for(int i = 1; i <= n; i ++) M = a[b[i].second] = a[b[i - 1].second] + (b[i].first != b[i - 1].first); // 离散化
for (int i = 1; i <= m; i ++) cin>>q[i].l>>q[i].r, q[i].id = i; // 离线
int blk = 0, l = 0, r = 0;
sort(q + 1, q + m + 1, cmp); // 莫队排序
for (int i = 1; i <= m; i++) {
if(get(q[i].l) == get(q[i].r)){ // 块内直接算
kkk = 0;
for(int j = 1; j <= M; j ++) h[j] = t[j] = 0; // 由于块内,之前与其左端点同一块的必然也是单独算,之前的对现在没用,直接清空
for(int j = q[i].l; j <= q[i].r; j ++){
if(!h[a[j]]) h[a[j]] = j;
t[a[j]] = j;
kkk = max(kkk, - h[a[j]] + t[a[j]]);
}
ans[q[i].id] = kkk;
continue;
}
if(blk != get(q[i].l)){ // 这是新的一块
cnt = 0;
for(int i = 1; i <= M; i ++) h[i] = t[i] = 0; // 清空
l = get_r(get(q[i].l));
r = l - 1;
blk = get(q[i].l);
}
while(r < q[i].r) add(++ r); // 从上次记录向右继续扩展
int p = l; kkk = 0;
while(p > q[i].l) add1(-- p); // 左端点单独重新扩展
ans[q[i].id] = max(cnt, kkk);
while(!stk.empty()){ // 恢复左端点操作前的数组
h[stk.top().first] = stk.top().second.second;
t[stk.top().first] = stk.top().second.first;
stk.pop();
}
}
for(int i = 1; i <= m; i ++) cout<<ans[i]<<'\n'; // 输出答案
return 0;
}
时间复杂度分析
让我们设块长为 \(B\)。
由于我们把询问拆成两部分,我们一部分一部分来看。
对于右端点直接连续扩展,有 \(\frac{n}{b}\) 块,每块最多让 \(r\) 右移 \(n\) 次,时间为 \(\mathcal O(n\frac{n}{b})\)。
对于左端点,有 \(q\) 次询问,每次询问最多向左跳 \(b\),时间为 \(\mathcal O(qb)\)。
综上,总的时间复杂度为 \(\mathcal O(n\frac{n}{b} + qb)\),由均值不等式可知,取 \(b = \dfrac{n}{\sqrt{b}}\),时间复杂度最优。
又一道例题 BZOJ P4358 permu
提示性给出方法:
Tips0
难以删除?回滚吧!Tips1
想一想再新增一个元素时,怎么求 $[l, r]$ 的最长值域连续段长度呢? 并查集?线段树?还是妙妙做法?Tips2
妙妙做法:两个数组 $pre_i$ 和 $nxt_i$ 记录此连续段头尾端点到 $i$ 的距离,更新 $i$。Tips3
你其实可以通过 $pre$ 和 $nxt$ 算出来头尾下标的。 尝试更新吧? 可能会有其他需要更新的吗?Solution
两个数组 $pre_i$ 和 $nxt_i$ 记录此连续段头尾端点到 $i$ 的距离。当前答案为:\(pre_i + nxt_i - 1\)。
当前头尾为:\(i - pre_i + 1\) 和 \(i + nxt_i - 1\)。
更新时,先更新 \(i\)(即当前点),再通过 \(i\) 更新两端的信息(这是因为只有两端的点对于下一段的拼接有作用)。
然后回滚就行。
Code
#include <bits/stdc++.h>
using namespace std;
#define get(x) ((x-1)/S+1)
#define get_l(x) ((x-1)*S+1)
#define get_r(x) min(n, x*S)
int n, m, S, cnt, kkk;
int a[50010], ans[50010], pre[50010], nxt[50010];
struct Node { int id, l, r; } q[50010];
bool vis[50010];
stack<Node> stk;
bool cmp(const Node& a, const Node& b) { return get(a.l) == get(b.l) ? a.r < b.r : get(a.l) < get(b.l); }
void add(int x){
pre[x] = pre[x - 1] + 1, nxt[x] = nxt[x + 1] + 1;
cnt = max(cnt, pre[x] + nxt[x] - 1);
pre[x + nxt[x] - 1] = nxt[x - pre[x] + 1] = pre[x] + nxt[x] - 1;
}
void add1(int x){
stk.push({x, pre[x], nxt[x]});
pre[x] = pre[x - 1] + 1, nxt[x] = nxt[x + 1] + 1;
kkk = max(kkk, pre[x] + nxt[x] - 1);
stk.push({x + nxt[x] - 1, pre[x + nxt[x] - 1], nxt[x + nxt[x] - 1]});
stk.push({x - pre[x] + 1, pre[x - pre[x] + 1], nxt[x - pre[x] + 1]});
pre[x + nxt[x] - 1] = nxt[x - pre[x] + 1] = pre[x] + nxt[x] - 1;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
cin>>n>>m;
S = sqrt(n);
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
int blk = 0, l = 0, r = 0;
sort(q + 1, q + m + 1, cmp);
for (int i = 1; i <= m; i++) {
if(get(q[i].l) == get(q[i].r)){
for(int j = q[i].l; j <= q[i].r; j ++) pre[a[j] + 1] = nxt[a[j] + 1] = pre[a[j] - 1] = nxt[a[j] - 1] = pre[a[j]] = nxt[a[j]] = 0;
for(int j = q[i].l; j <= q[i].r; j ++){
int x = a[j];
pre[x] = pre[x - 1] + 1, nxt[x] = nxt[x + 1] + 1;
ans[q[i].id] = max(ans[q[i].id], pre[x] + nxt[x] - 1);
pre[x + nxt[x] - 1] = nxt[x - pre[x] + 1] = pre[x] + nxt[x] - 1;
}
continue;
}
if(blk != get(q[i].l)){
cnt = 0;
for(int i = 1; i <= n; i ++) pre[i] = nxt[i] = 0;
l = get_r(get(q[i].l));
r = l - 1;
blk = get(q[i].l);
}
while(r < q[i].r) add(a[++ r]);
int p = l; kkk = 0;
while(p > q[i].l) add1(a[-- p]);
ans[q[i].id] = max(cnt, kkk);
while(!stk.empty()){
pre[stk.top().id] = stk.top().l;
nxt[stk.top().id] = stk.top().r;
stk.pop();
}
}
for(int i = 1; i <= m; i ++) cout<<ans[i]<<'\n';
return 0;
}
这两道题均为入门,回滚莫队可以更难,留与读者自己了解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号