一维理想器件的电势分布问题
研究背景
最近两三个月,本人在断断续续地学习一维MOS器件的数值模拟仿真 (仅Poisson方程),主要细节见
https://www.cnblogs.com/ghzhan/articles/17031958.html
https://www.cnblogs.com/ghzhan/articles/17368238.html
https://www.cnblogs.com/ghzhan/articles/17372907.html
当下图器件区域掺杂浓度分别为 1E20 - 5E19 - 1E20 时,器件电势分布和PLDOS如下图所示
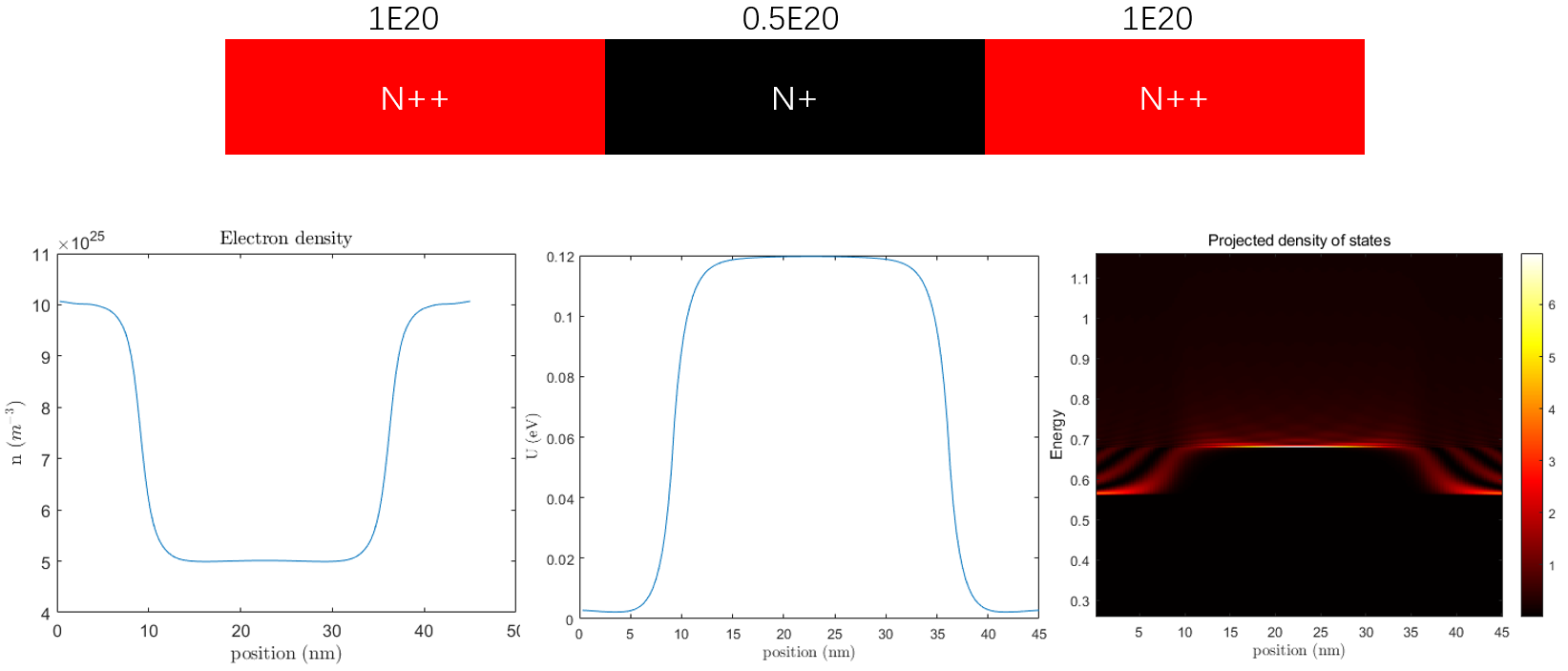
我将试着器件中间区域的掺杂浓度设为 0,即本征浓度时,得到器件电势分布如图所示,
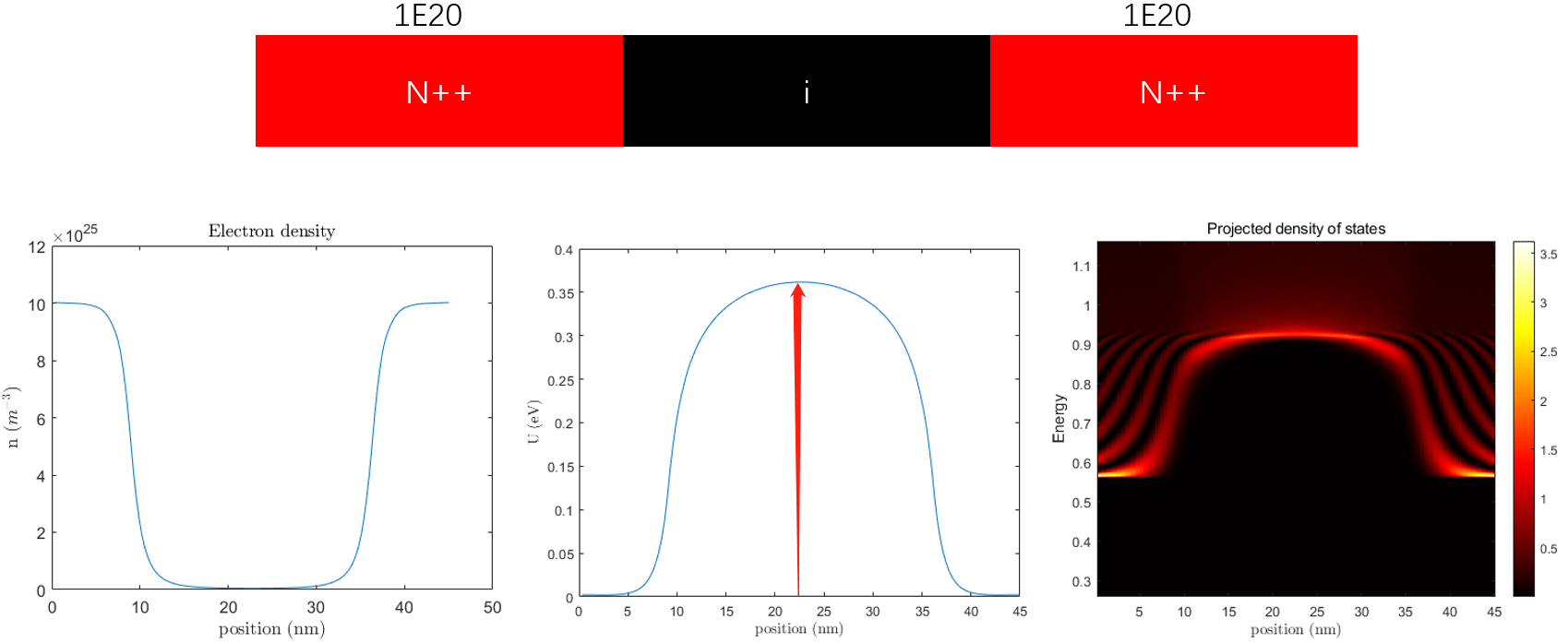
研究问题
最开始碰到这个问题,我尝试用不同的方法去检验我自己的逻辑是否自洽,便用了最简单的PN结去测试,测试的结果如下
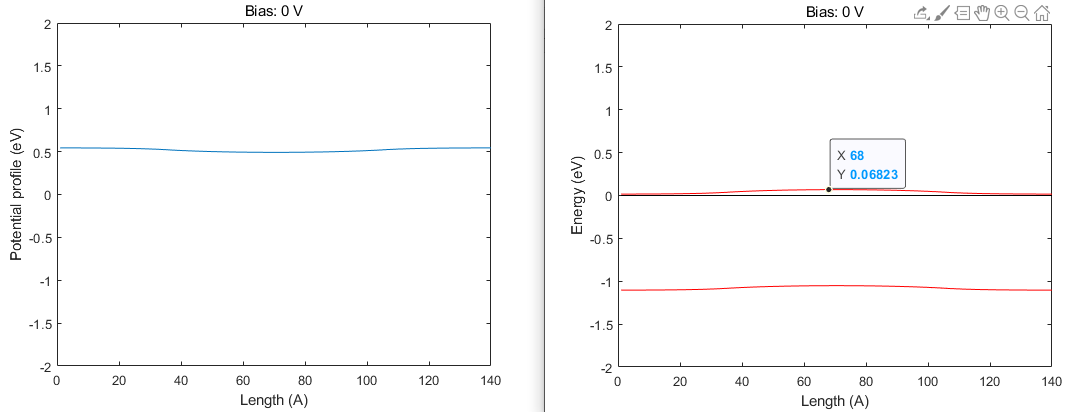
接着(....过了n天),我用比较成熟的程序例如 Sentaurus/GTS 去搭建这样的器件模型测试, 尝试着找到它们的联系, 最后也失败了,因为我没有搭建好这样的一维理想器件模型,直接是用的官方例子给的2D MOSFET, 这些器件都加了栅极Gate的模型(这个在仿真细节处理上很关键,后面我再讲).
接着(....又过了n天),我翻遍了github,找到一位韩国学者很早之前做的项目 (NEGF_DGMOS)[1],运行了他们的MATLAB源代码, 才渐渐地明白了...
我的核心问题是,器件中间是本征区域,为啥不是正好 Eg/2?
GTS 结果
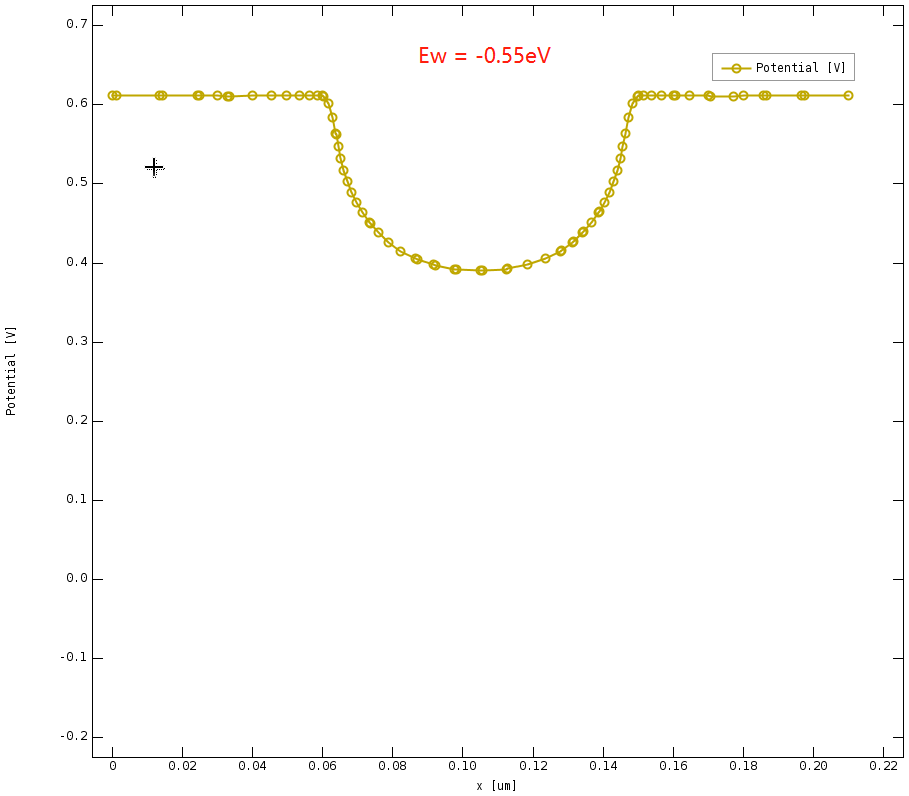
采用官方给出的二维N型MOSFET例子,Ew (与栅极功函数有关)分别设置 -0.55和 0 eV, 计算器件转移曲线
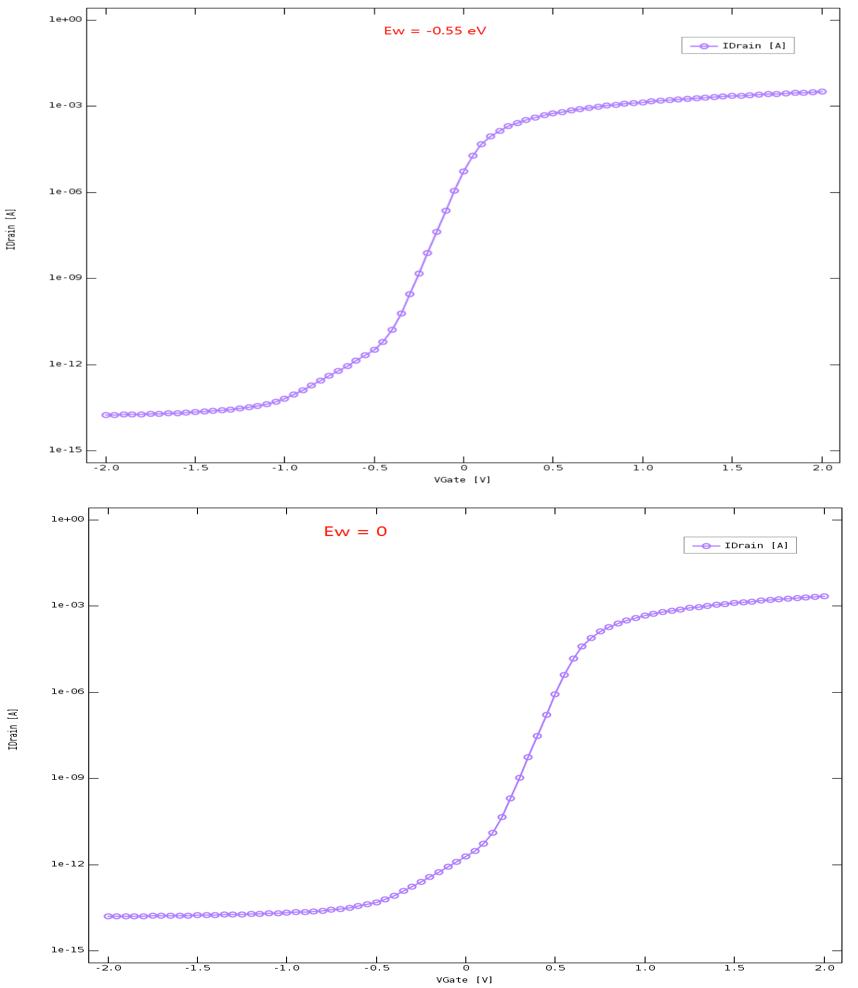
下面再来分析器件的电势分布, 先将栅极电压和源漏电压均设为 0 V.
当 Ew = -0.55 eV 时, 器件中央的电势分布为
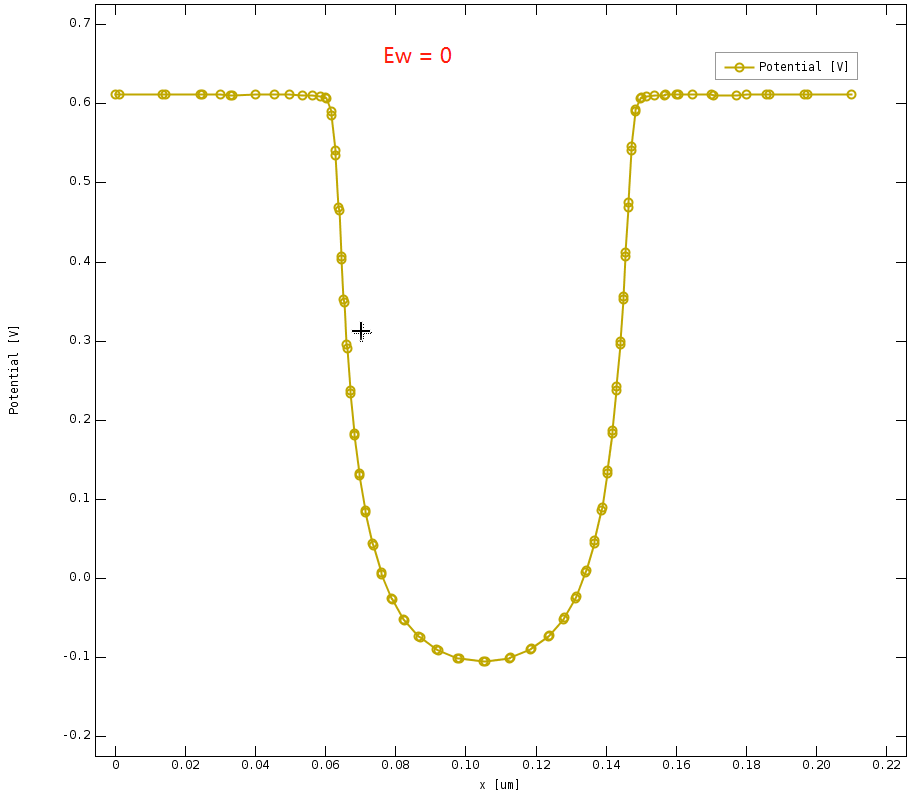
NEGF_DGMOS
NEGF_DGMOS 是二维 Double Gate 器件的NEGF仿真.
逐句地分析栅极电势部分源码. 因为对于器件模型数值计算,得必须设置好边界条件,栅极电势通常是采用第一类边界条件。
点击查看代码
%% bias
Vg_bias = 0.1; % Vgs [V]
% 陛加 - workfunction: 4.1 eV
% 角府能 - electron affinity: 4.05 eV, bandgap: 1.11 eV
% barrier height = 4.1 - (4.05 + 1.11/2) = -0.505 eV -> 0.505 V
Vg_barrier = 0.505; % [V]
Vgs = Vg_barrier + Vg_bias; % 霸捞飘
当设置 Vg_bias 为 0 时,栅极电势为 Vgs = 0.505 V, 切线在二维器件中央, 第一步Poisson方程初始化得到的电势分布为
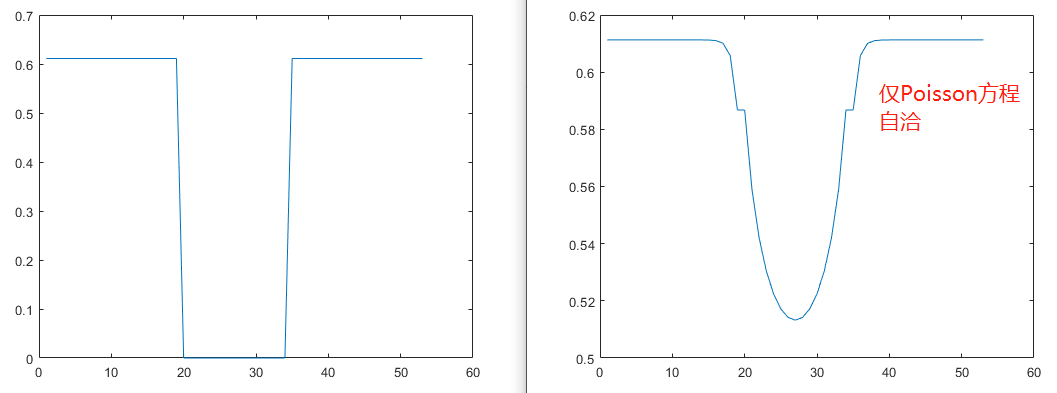
再根据NEGF方程计算电子密度,对电势进行迭代收敛,得到最终的电势分布为:
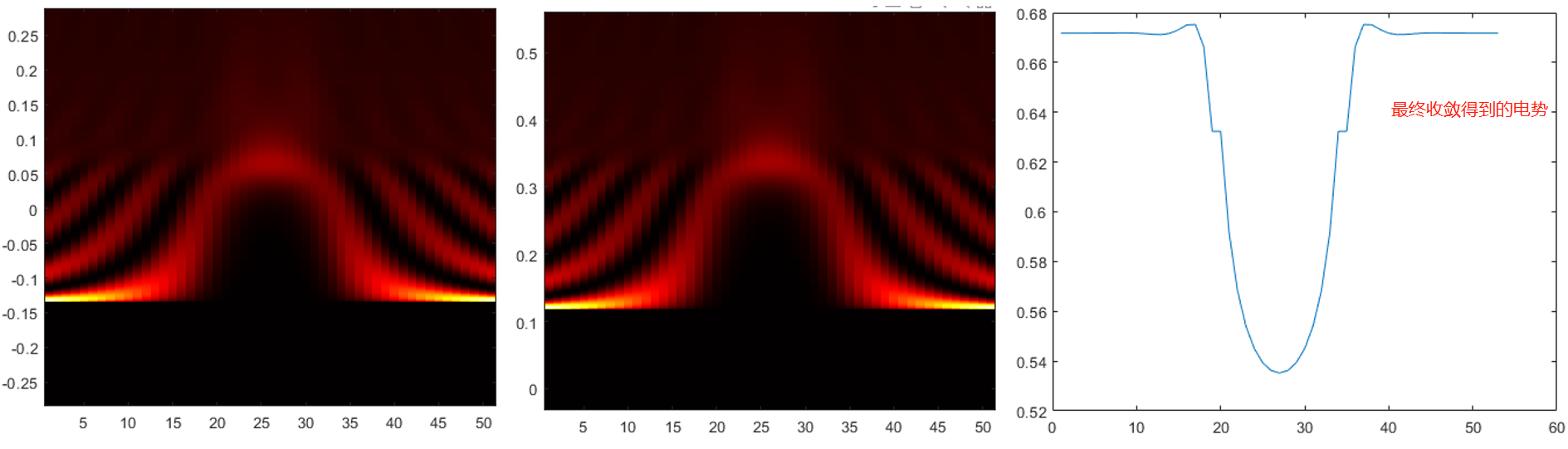
于是,我们再来设置 Vgs = 0, 初始化得到的电势为
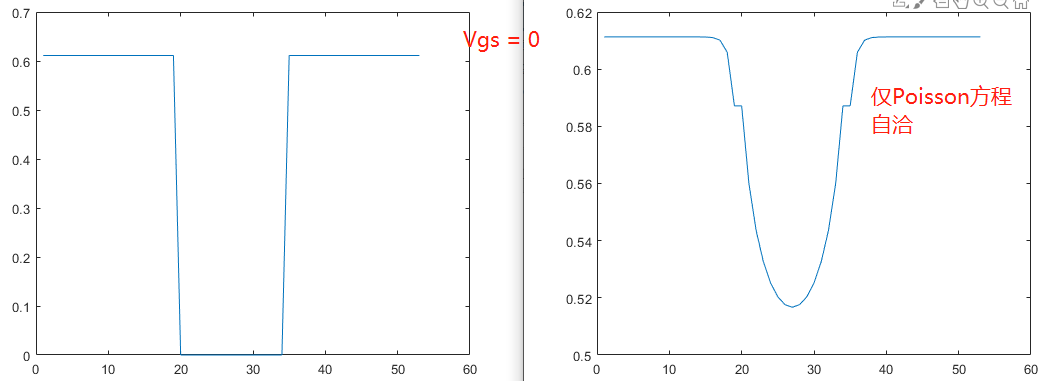
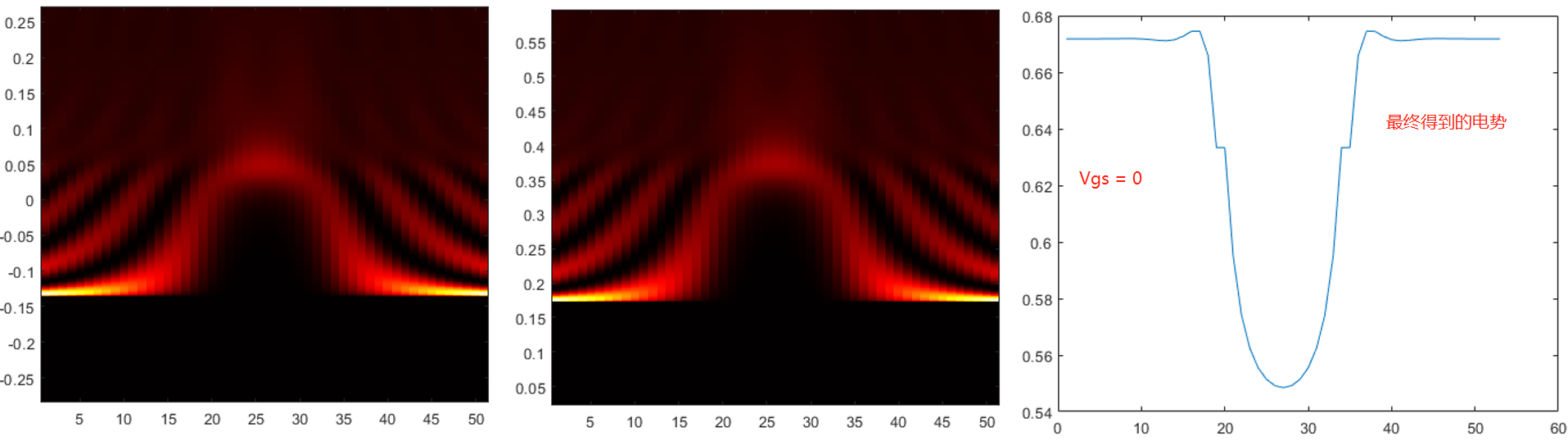
最终的电势分布为:
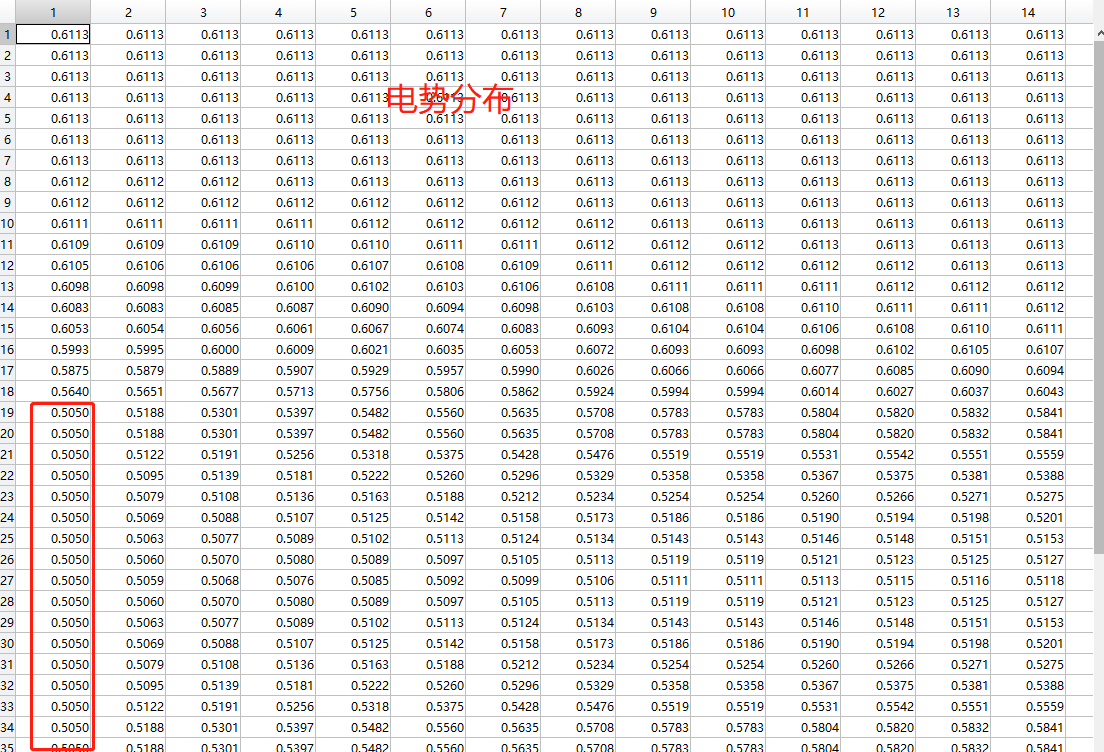
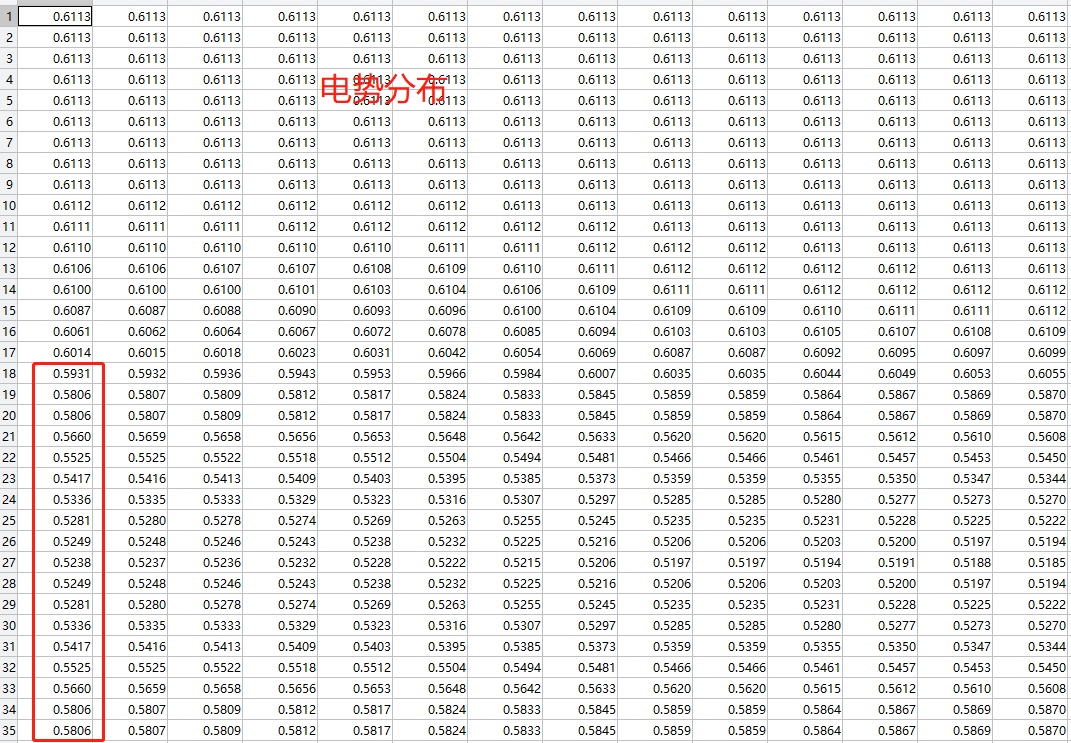
为了验证 Vgs = 0 V 在边界数值上不起作用, 我们不妨再设置 Vgs = 0.0001 V 来测试, 因为该栅压下的电势分布应该和 0V 接近. 第一步初始化得到的电势为
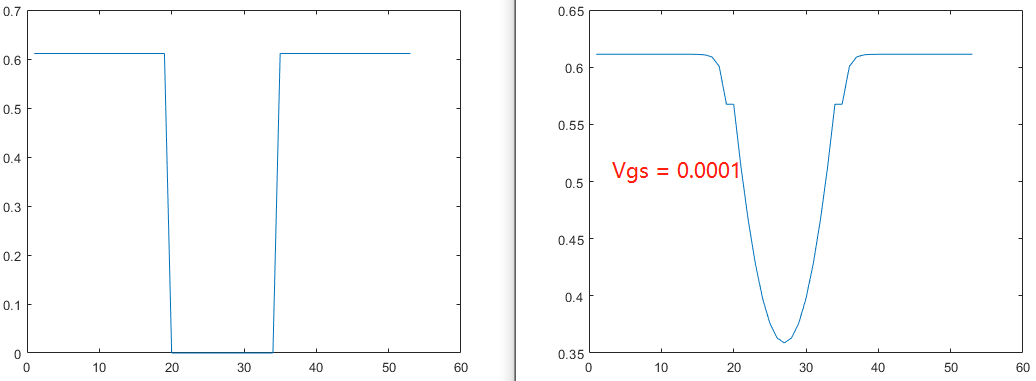
电势具体数值为:
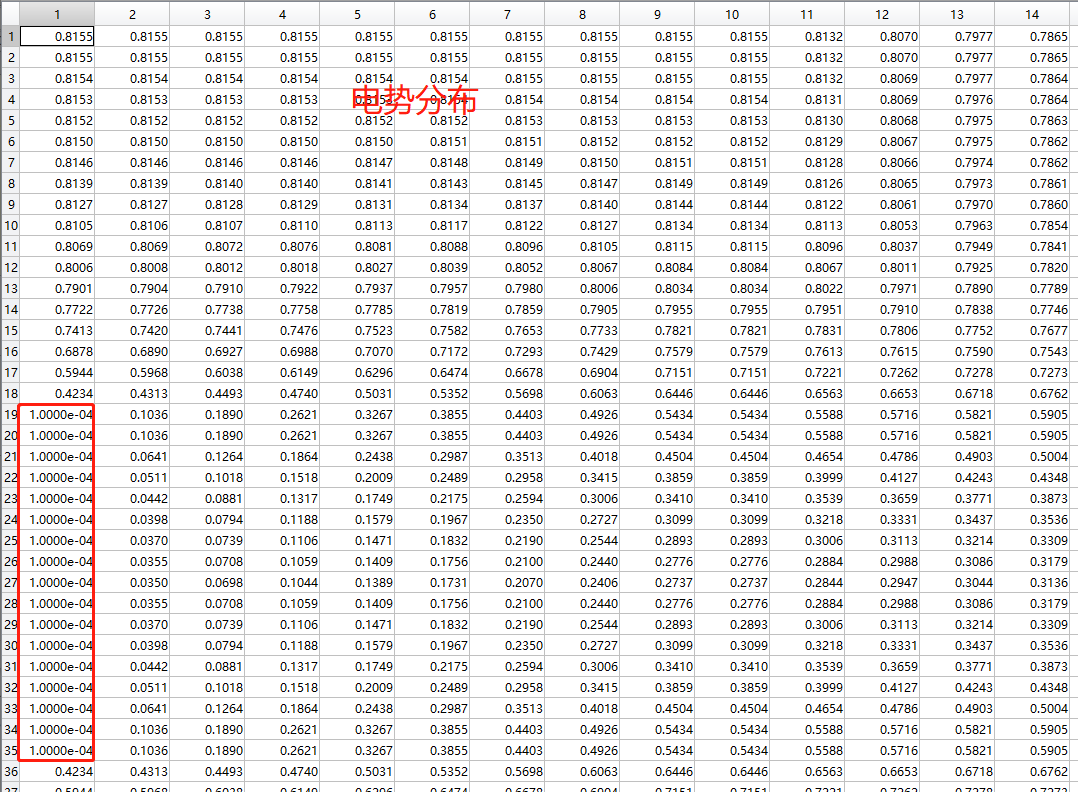
可以发现,栅极电势被限定为 0.0001 V. 这与 Vgs = 0 V的情况截然不同.
通过NEGF-Poisson方程自洽收敛,可以得到最终的电势分布为:
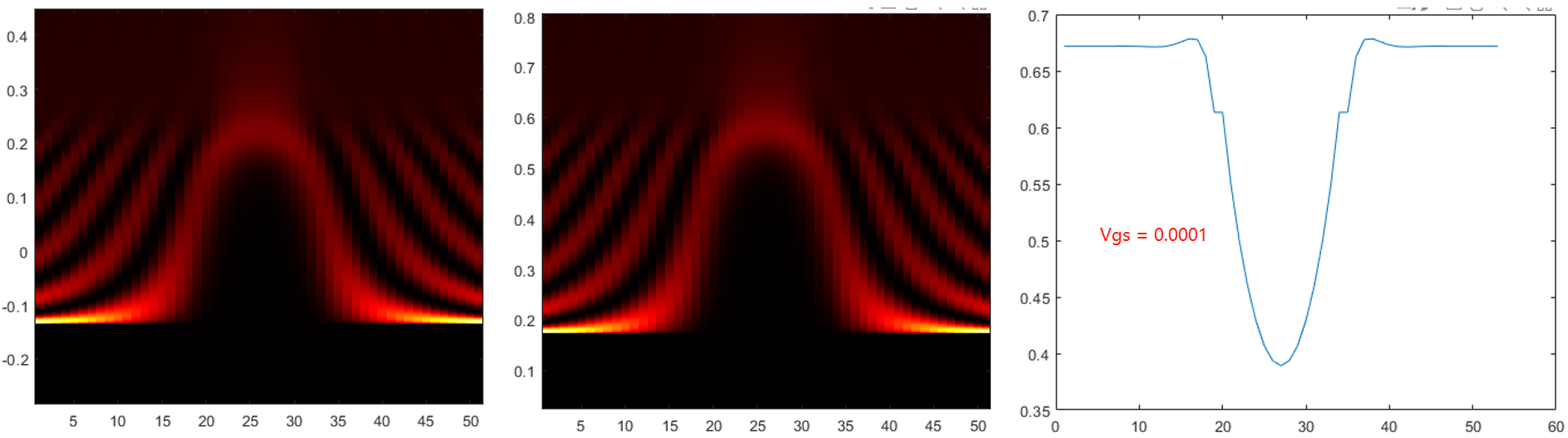
通过上述这个二维例子,能较好地解答我们之前的问题. 因为对于一维理想MOS器件,不存在栅极区域,即等同于该二维器件 Vgs = 0V的情况(没有栅极边界限制),二者本质上是一样的。根据 DGMOS 的数值仿真结果,其源漏与本征沟道区域电势差也不是 Eg/2, 这与一维理想器件仿真得到的电势分布趋势一致.
总结
对于一维理想器件模型,由于没有栅极边界条件,其电势分布需要通过Poisson方程自洽求得,重掺源漏与本征沟道电势差值并不是所谓的 Eg/2. 不过理论上,当本征沟道区域足够长时,其差值应该接近 Eg/2. 如下图:
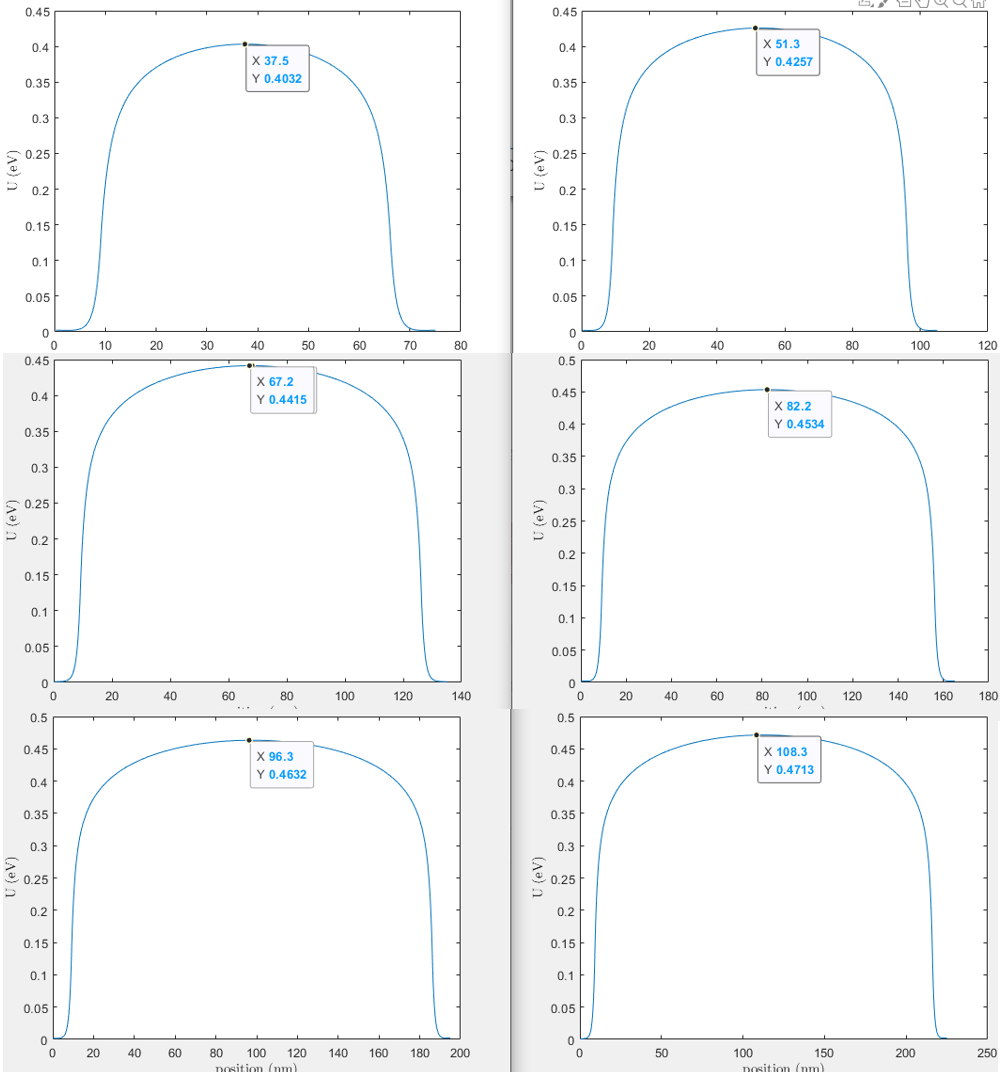
综上可知, 通过栅控(例如金属功函数,氧化层厚度,介电常数等)来调节器件内部的电势分布,从而实现所需要的功能.
参考文献
[1] https://github.com/SungHyunCha/NEGF_DGMOS
[2] https://docs.quantumatk.com/manual/Types/IVCharacteristics/IVCharacteristics.html
附件
点击查看代码1
%test Ec = 1.12/2;
clear
tic
%Constants (all MKS, except energy which is in eV)
hbar=1.054571817e-34;
q=1.602176634e-19; %C
epsil=10*8.854187817E-12;%F/m
kT=0.025852; %300K, eV
m=0.25*9.1093837015e-31;%kg
n0= m*kT*q/(2*pi*(hbar^2));
Ec = 1.12/2;
%inputs
a=3e-10;
t=(hbar^2)/(2*m*(a^2)*q);
beta=q*a*a/epsil;
NL=30;NC=90;NR=NL;
Np=NL+NC+NR;XX=a*1e9*[1:1:Np];
mu=Ec + 0.31251598;Fn=mu*ones(Np,1);
%mu=.0;Fn=mu*ones(Np,1);
Nd = 2*(n0^1.5)*Fhalf((mu-Ec)/kT);
Nd = Nd*[ones(NL,1);0.*ones(NC,1);ones(NL,1)];
%Nd=zeros(Np,1);
%mu=Ec + 0.15251598;Fn=mu*ones(Np,1);
%d2/dx2 matrix for Poisson solution
D2=-(2*diag(ones(1,Np)))+(diag(ones(1,Np-1),1))+(diag(ones(1,Np-1),-1));
D2(1,1)=-1;D2(Np,Np)=-1;%zero field condition
% Boundary conditions (Neumann homogeneous)
%D2(1,2)=2; D2(Np,Np-1)=2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Initial H00 H01 %%%%%%%%%%%%%%%%%%%%%%%%%%%%
W = 1;
H00 = zeros(W,W);
H01 = zeros(W,W);
for j = 1:W
H00(j,j) = 2*t + Ec;
H01(j,j) = -t;
if j < W
H00(j,j+1) = -t;
H00(j+1,j) = -t;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%% Band of each slice %%%%%%%%%%%%%%%%%%%%%%%%%%%%
Nk = 200;
i_E = linspace(-pi,pi,Nk);
res = zeros(Nk,W);
for i = 1:Nk
Ham = H00 + H01*exp(1j*i_E(i)) + H01'*exp(-1j*i_E(i));
val = eig(Ham);
res(i,:) = val';
end
figure;
plot(i_E,res);
%ylim([0,1]);
xlim([-pi,pi]);
xlabel('k');
ylabel('Energy [t]')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%% Initial Ham Full matrix %%%%%%%%%%%%%%%%%%%%%%%%%
L = Np;
Ham = zeros(W*L,W*L);
for j = 1:L
Ham(j*W-W+1:j*W,j*W-W+1:j*W) = H00;
if j < L
Ham(j*W-W+1:j*W,j*W+1:j*W+W) = H01;
Ham(j*W+1:j*W+W,j*W-W+1:j*W) = H01';
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Hamiltonian matrix
%T=(2*t*diag(ones(1,Np)))-(t*diag(ones(1,Np-1),1))-(t*diag(ones(1,Np-1),-1));
%energy grid
N_E=501;
E = linspace(-0.3+Ec,0.6+Ec,N_E);
dE = E(2)-E(1);
eta = 1e-8;
%self-consistent calculation
U=[zeros(NL,1);.2*ones(NC,1);zeros(NR,1)];%guess for U
dU=0;
LDOS = zeros(N_E,Np);
change = 10;
while change > 0.001
%from U to n
SigmaL=zeros(Np);SigmaR=zeros(Np);
n = zeros(Np,1);
for i_E = 1:N_E
f0 = 2*n0*log(1+exp((mu-E(i_E))/kT));
ck=1-((E(i_E)+1j*eta-U(1)-Ec)/(2*t));ka=acos(ck);
SigmaL(1,1)=-t*exp(1i*ka);%gam1=1i*(SigmaL-SigmaL');
ck=1-((E(i_E)+1j*eta-U(Np)-Ec)/(2*t));ka=acos(ck);
SigmaR(Np,Np)=-t*exp(1i*ka);%gam2=1i*(SigmaR-SigmaR');
G = inv(((E(i_E)+1j*eta)*eye(Np))- Ham - diag(U)-SigmaL-SigmaR);
A=1i*(G-G');
rhoE = f0*diag(A)/(2*pi);
n = n + ((dE/a)*real(rhoE));
LDOS(i_E,:) = diag(A)/(2*pi);
end
%correction dU from Poisson
D=zeros(Np,1);
for i_E = 1:Np
z =(Fn(i_E)-U(i_E) - Ec)/kT;
D(i_E,1)=2*(n0^1.5)*((Fhalf(z+.1)-Fhalf(z))/.1)/kT;
end
dN = n - Nd + ((1/beta)*D2*U);
dU = (-beta)*(inv(D2-(beta*diag(D))))*dN;
U = U + 1*dU;
%check for convergence
%ind=(max(max(abs(dN))))/(max(max(Nd)));
change = max(max(abs(dU)))
end
figure
plot(XX,n)
xlabel('position (nm)', 'Interpreter', 'latex');
ylabel('n ($m^{-3}$)', 'Interpreter', 'latex');
title('Electron density', 'Interpreter', 'latex');
set(gca,'Fontsize',12)
figure;
plot(XX,U)
xlabel('position (nm)', 'Interpreter', 'latex');
ylabel('U (eV)', 'Interpreter', 'latex');
figure;
imagesc(XX,E,LDOS);
xlabel('position (nm)', 'Interpreter', 'latex');
ylabel('Energy');
title('Projected density of states');
axis xy
colormap('hot');
colorbar
toc
save fig31
hold on
点击查看代码2 PN结
%%%%%%
% 2023/5/5
% n-i-n device test.
clear;
epsilon = 1.05*1e-12; %F/cm
q = 1.6*1e-19;% C
kT = 0.02585;% eV
n0 = 1.45*1e10; %cm^-3
theta = 1e-8; %cm
m = 140;
Na = 2e19; %cm^-3 3.7126e+19
Nd = Na;
Eg = 1.12;%eV
Vds = 0; % V Equilibrium
%Vds = 1; % V Positive voltage
%Vds = -1;% V Negative voltage
Vp = Vds/2; Vn = -Vds/2;
VP = Vp - kT*log(Na/n0);
VP = 0;
VN = Vn + kT*log(Nd/n0);
%%% pn
%Na = Na*[ones(m/2,1);zeros(m/2,1)];
%Nd = Nd*[zeros(m/2,1);ones(m/2,1)];
%%% p-i-n
Na = 0*[ones(m/4,1);zeros(m/2,1);zeros(m/4,1)];
Nd = [Nd*ones(m/4,1);0.0*Nd*ones(m/2,1);Nd*ones(m/4,1)];
V=zeros(m,1);
V(1:m/4,1)=VN; %VP has to be predefined as in (7)
V(3*m/4+1:m,1)=VN; %VN has to be predefined as in (8)
D2=-(2*diag(ones(1,m)))+(diag(ones(1,m-1),1))+(diag(ones(1,m-1),-1));
% Diriclet Boundary condition
V0 = [VN;zeros(m-2,1);VN];
% Neumann Boundary condition
%D2(1,1)=-1;D2(m,m)=-1;
%V0 = zeros(m,1);
beta = q*theta^2/epsilon;
%figure;
Error = 10;
while Error > 1e-15
%hold on;
%plot(V)
n = n0*exp((V-Vn)/kT);
%drho_dv = -2*n0/kT*cosh(V/kT);
drho_dv = -1/kT*n;%-n0/kT*exp((Vp-V)/kT);
%rho = Nd - Na - 2*n0*sinh(V/kT);
rho = Nd - n;
%%%% Newton-Raphon Method
M = D2 + diag(beta*drho_dv);
R = -(D2*V + V0 + beta*rho);
dv = M\R;
V = V + 0.1*dv;
Error = norm(dv,2)/sqrt(m);
end
theta = 1e8*theta;
figure;
plot(V);
xlabel('Length (A)');
ylabel('Potential profile (eV)');
ylim([-2,2])
title(['Bias: ', num2str(Vds),' V']);
figure;
plot(theta*[1:1:m],rho);
xlabel('Length (A)');
ylabel('charge density');
title(['Bias: ', num2str(Vds),' V']);
figure;
plot(theta*[1:1:m],n);
xlabel('Length (A)');
ylabel('electron density');
title(['Bias: ', num2str(Vds),' V']);
figure;
plot(theta*[1:1:m],-V+Eg/2,'r',theta*[1:1:m],-V-Eg/2,'r')
hold on
plot(theta*[1:1:m],Vn*ones(m,1),'k-',theta*[1:1:m],Vp*ones(m,1),'k-');
xlabel('Length (A)');
ylabel('Energy (eV)');
ylim([-2,2])
title(['Bias: ', num2str(Vds),' V']);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号