一维PN结的数值模拟(非平衡态)

写在前面

五一期间复习了一维 PN 结的poisson 方程数值模拟 (https://www.cnblogs.com/ghzhan/articles/17368238.html), 今天打算把非平衡态输运的情况也记录一下, 当然这些都是基于经典图像下的. 严格点的话，需要对 PN 结进行量子框架下的输运计算(例如DFT-NEGF等), 不过这些经典图像对理解传统器件输运已经足够了！

理想 PN 结非平衡态

对于非平衡态时, 其载流子浓度为:

$$n=n_i \mathbf{exp}(\frac{E_{Fn}-E_i}{k_0T})\\ p=n_i \mathbf{exp}(\frac{E_{i}-E_{Fp}}{k_0T})\\ n\cdot p = n_i^2\mathbf{exp}\frac{E_{Fn}-E_{Fp}}{k_0T}$$

其中, $n_i$ 是本征载流子浓度, $E_{Fn},E_{Fp}$ 分别是 PN 结两端的准费米能级. $E_i = -qV(x), E_{Fn}=-qV_n, E_{Fp}=-qV_p$. 且 $V_{p}-V_{n}= V_{ds}$, $V_{ds}$ 为 PN 结两端的偏压.

将上述载流子公式代入 Poisson 方程

$$\frac{d^2V}{dx^2} = -\frac{\rho}{\varepsilon} \\ \rho=q(p-n+N_d-N_a)\\ =q\left(n_i \mathbf{exp}(\frac{V_p-V}{k_0T/q})-n_i \mathbf{exp}(\frac{V-V_n}{k_0T/q}) + N_d -N_a\right)$$

$\partial \rho/\partial V$ 为:

$$\frac{\partial\rho}{\partial V}= -\frac{q^2n_i}{k_0T}\left(\mathbf{exp}(\frac{V-V_n}{k_0T/q} )+\mathbf{exp}(\frac{V_p-V}{k_0T/q})\right)$$

再根据 Newton-Raphason 方法迭代求解得到电势分布.

结果分析

平衡态时,

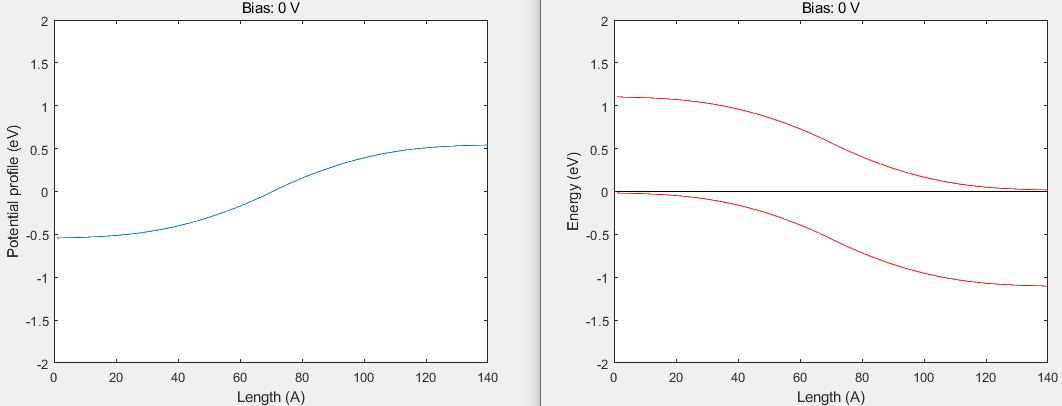
正偏 1V 时,

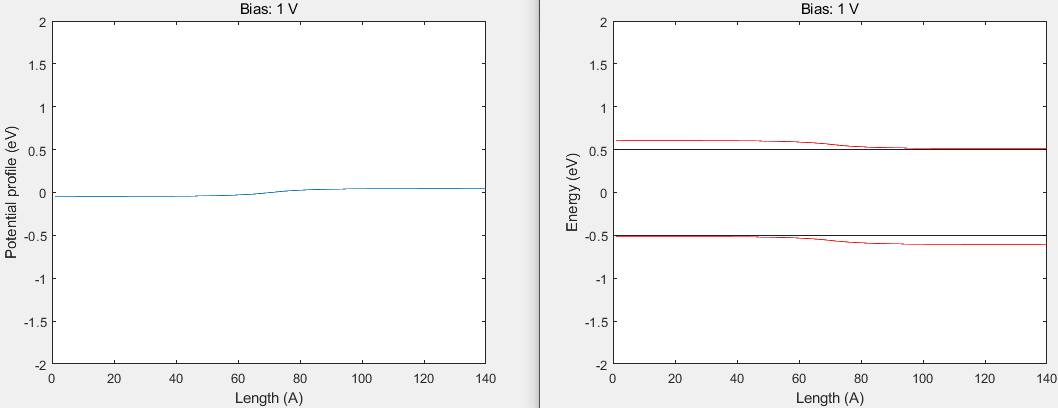
反偏 -1V 时,

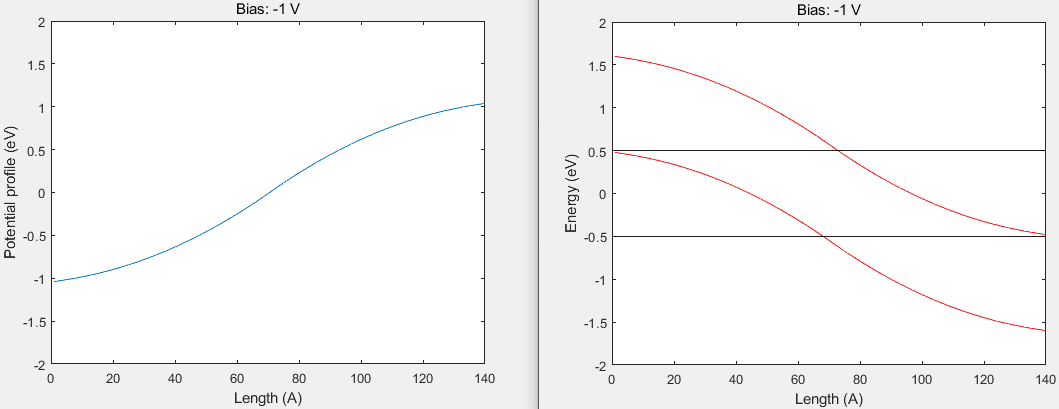
该结果与QuantumATK 官网例子大致相同. https://docs.quantumatk.com/tutorials/silicon_pn_junction/silicon_pn_junction.html

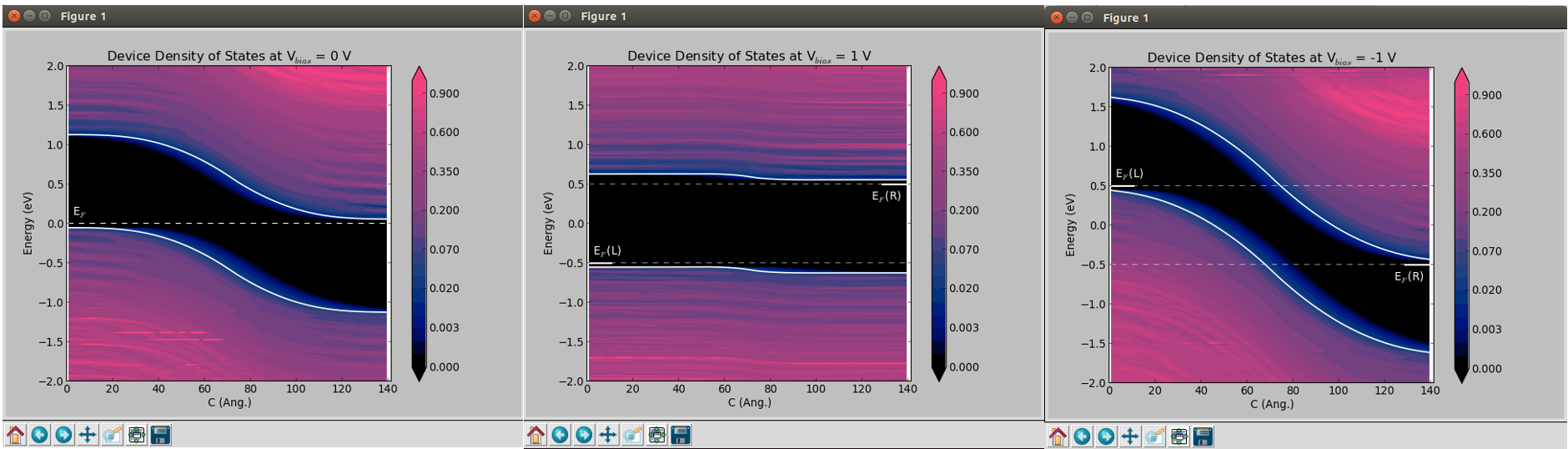
附件

点击查看代码

%%%%%%
% 2023/5/4
% The Newton-Raphson method for PN diode.
% This code is modified by ghzhan(ghzphysics@163.com) based on the Ref. 1.
% This code repoduce the results in the Ref1
% This code also repoduce the result on Website: https://docs.quantumatk.com/tutorials/silicon_pn_junction/silicon_pn_junction.html
% Ref 1: https://doi.org/10.7227/IJEEE.44.1.3
%
clear;
epsilon = 1.05*1e-12; %F/cm
q = 1.6*1e-19;% C
kT = 0.02585;% eV
n0 = 1.45*1e10; %cm^-3 
theta = 1e-8; %cm
m = 140;
Na = 2e19; %cm^-3
Nd = Na;
Eg = 1.12;%eV

%Vds = 0; % V Equilibrium
%Vds = 1; % V Positive voltage
Vds = -1;% V Negative voltage

Vp = Vds/2; Vn = -Vds/2;
VP = Vp - kT*log(Na/n0);
VN = Vn + kT*log(Nd/n0);

%%% pn
Na = Na*[ones(m/2,1);zeros(m/2,1)];
Nd = Nd*[zeros(m/2,1);ones(m/2,1)];
%%% p-i-n
%Na = Na*[ones(m/4,1);zeros(m/2,1);zeros(m/4,1)];
%Nd = Nd*[zeros(m/4,1);zeros(m/2,1);ones(m/4,1)];

V=zeros(m,1);
V(1:m/2,1)=VP;    %VP has to be predefined as in (7)
V(m/2+1:m,1)=VN;  %VN has to be predefined as in (8)
D2=-(2*diag(ones(1,m)))+(diag(ones(1,m-1),1))+(diag(ones(1,m-1),-1));
V0 = [VP;zeros(m-2,1);VN]; % Boundary condition
beta = q*theta^2/epsilon;

%figure;
Error = 10;
while Error > 1e-15
    %hold on;
    %plot(V)
    
    %drho_dv = -2*n0/kT*cosh(V/kT);
    drho_dv = -n0/kT*exp((V-Vn)/kT)-n0/kT*exp((Vp-V)/kT);
    %rho = Nd - Na - 2*n0*sinh(V/kT);
    rho = Nd - Na - n0*exp((V-Vn)/kT) + n0*exp((Vp-V)/kT);
    %%%% Newton-Raphon Method
    M = D2 + diag(beta*drho_dv);
    R = -(D2*V + V0 + beta*rho);
    dv = M\R;
    
    V = V + 0.1*dv;
    Error = norm(dv,2)/sqrt(m);
end

figure;
plot(V);
xlabel('Length (A)');
ylabel('Potential profile (eV)');
ylim([-2,2])
title(['Bias: ', num2str(Vds),' V']);

figure;
theta = 1e8*theta;
plot(theta*[1:1:m],-V+Eg/2,'r',theta*[1:1:m],-V-Eg/2,'r')
hold on
plot(theta*[1:1:m],Vn*ones(m,1),'k-',theta*[1:1:m],Vp*ones(m,1),'k-');
xlabel('Length (A)');
ylabel('Energy (eV)');
ylim([-2,2])
title(['Bias: ', num2str(Vds),' V']);