MBD笔记：放大器与滤波器模型设计

目录

本文主要基于Simulink，从模型设计角度讲解放大器、滤波器.

OP放大器的模型设计

OP放大器（Operational Amplifier，运算放大器，简称运放）：用于放大微小信号的基础单元. 电路图符号、实物图、引脚图：

img

OP放大器特点：具有很高的放大系数，在电路中结合反馈网络组成某种功能模块，其输出信号可以是输入信号的加减运算或微积分等数学运算的结果. 可由分立器件，如二极管、三极管、场效应管、晶闸管、IGBT等组成，也可在芯片中实现.

  • 与Simulink> Gain模块区别

OP放大器符号类似于Gain模块，都能放大信号.

区别：Gain模块放大的是一个信号，OP放大器放大的是同相输入（V1）和反向输入（V2）的差（差动输入）. OP放大器利用了反馈，而Gain模块没有.

  • 输入、输出关系

设OP放大器的放大系数A，输出V0，那么：

\[\tag{1} V_0=A\times (V_1-V_2) \]

A通常为\(1000~10^6\)，用分贝符号表示60~120dB.

OP放大器、放大系数

OP放大器常采用负反馈，即将输出返回至反相输入端，如下图：

img

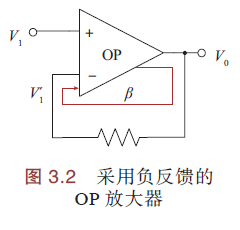
设反馈系数β，则OP放大器输出：

\[\begin{split} V_0 &= A\times (V_1-V_1'), V_1' = βV_0\\ \implies V_0 &= A\times (V_1-βV_0)\\ AV_1 &= V_0(1+Aβ)\\ \frac{V_0}{V_1} &= \frac{A}{1+Aβ} \tag{2} \end{split} \]

反馈系数β

\[β=\frac{输出电压}{反馈电压} \]

反馈系数β=1

β=1 <=> 反馈电路直接将输出返回至输入

OP放大器其电压跟随作用. 电压跟随电路：

img

\[\begin{split} \frac{V_0}{V_1} &= \frac{A}{1+βA}, 1\ll A\\ &= \frac{A}{1+A} ≈ \frac{A}{A}=1 \tag{3} \end{split} \]

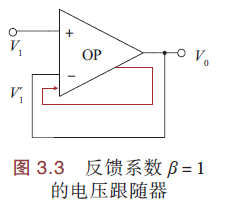
反馈系数β=0.5

\[\tag{4} \begin{split} \frac{V_0}{V_1} &= \frac{A}{1+βA}, 1\ll A\\ &= \frac{A}{1+0.5A} ≈ \frac{A}{0.5A}=2=\frac{1}{β} \end{split} \]

∵\(1\ll A\)
∴\(1+βA≈A\)
∴电路输出输入比值为\(1/β (0<β<1)\)

通过电阻的比率设置反馈系数β

如下图，电阻R1,R2串联，反馈系数β：

\[\begin{aligned} V_0 &= (R_1+R_2)i, V_1' = R_1\times i\\ V_1':V_0 &= R_1 : (R_1+R_2)\\ ∴β &= \frac{V_1'}{V_0}=\frac{R_1}{R_1+R_2} \tag{5} \end{aligned} \]

img

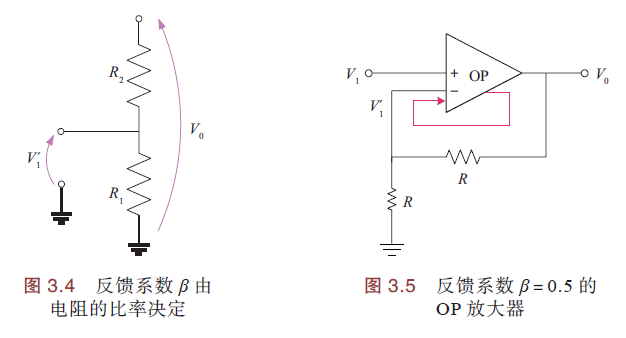
当反馈系数β=0.5时，可得\(R_1=R_2\)

用Simscape设计OP放大器模型

Simscape是MathWorks公司推出的物理系统建模和仿真工具，基于MATLAB/Simulink 平台. 能通过物理网络方式构建模型，而不是传统数学方程或信号流，从而更直观模拟机械、电气等物体系统的行为.

β=1的OP放大器模型

目的：验证β=1时，\(V_0,V_1\)是否符合电压跟随特性

Simulink模型文件名：Op001.slx

所用模块：

img
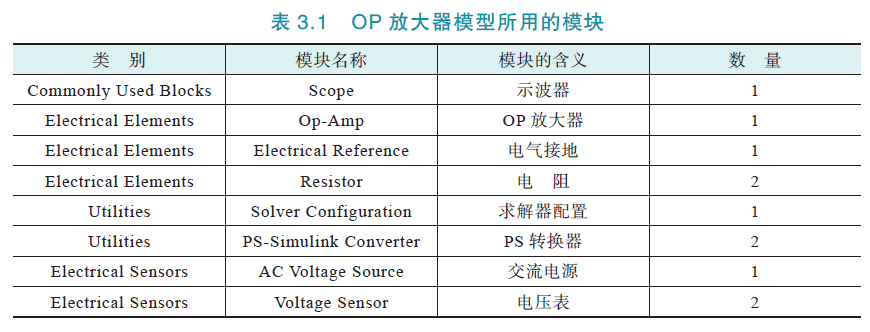
其中，
1）对于Simscape模型，通常必须包含Solver Configuration模块以启用局部求解器；
2）PS转换器模块 用于连接Simscape模块和Simulink模块，将物理信号转换Simulink输出信号，才能直连Simulink示波器或其他模块;

建模如下：

img
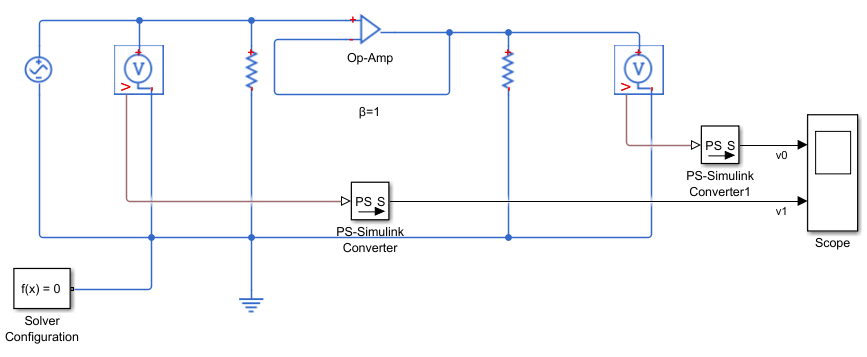
其中，停止时间设为为0.2（s）；AC Voltage Source（交流电源）振幅12V，频率10Hz（1Hz=2π rad/s）；2个电阻均设为100Ω；

仿真结果：
img
注：v0输出，v1输入

可看出输入电压、输出电压振幅±12V；因为交流电源频率10Hz且停止时间0.2s，所以运行波形运行了2个周期；β=1时放大系数为1，没有相位延时

β=0.5的OP放大器模型

文件：Op002.slx

反馈回路上，\(R_1=R_2=100Ω\)时，\(β=\frac{R_1}{R_1+R_2}=0.5\)

建模如下：

img

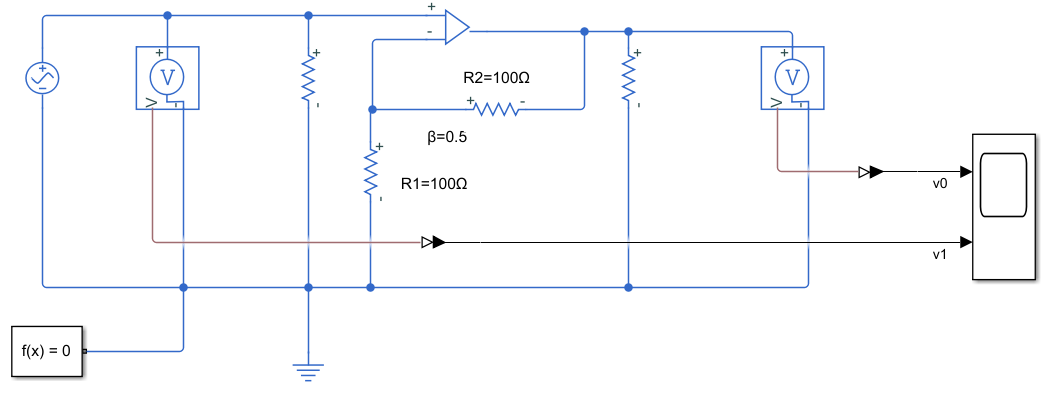
β=0.5时，电路放大系数2

仿真结果：

img

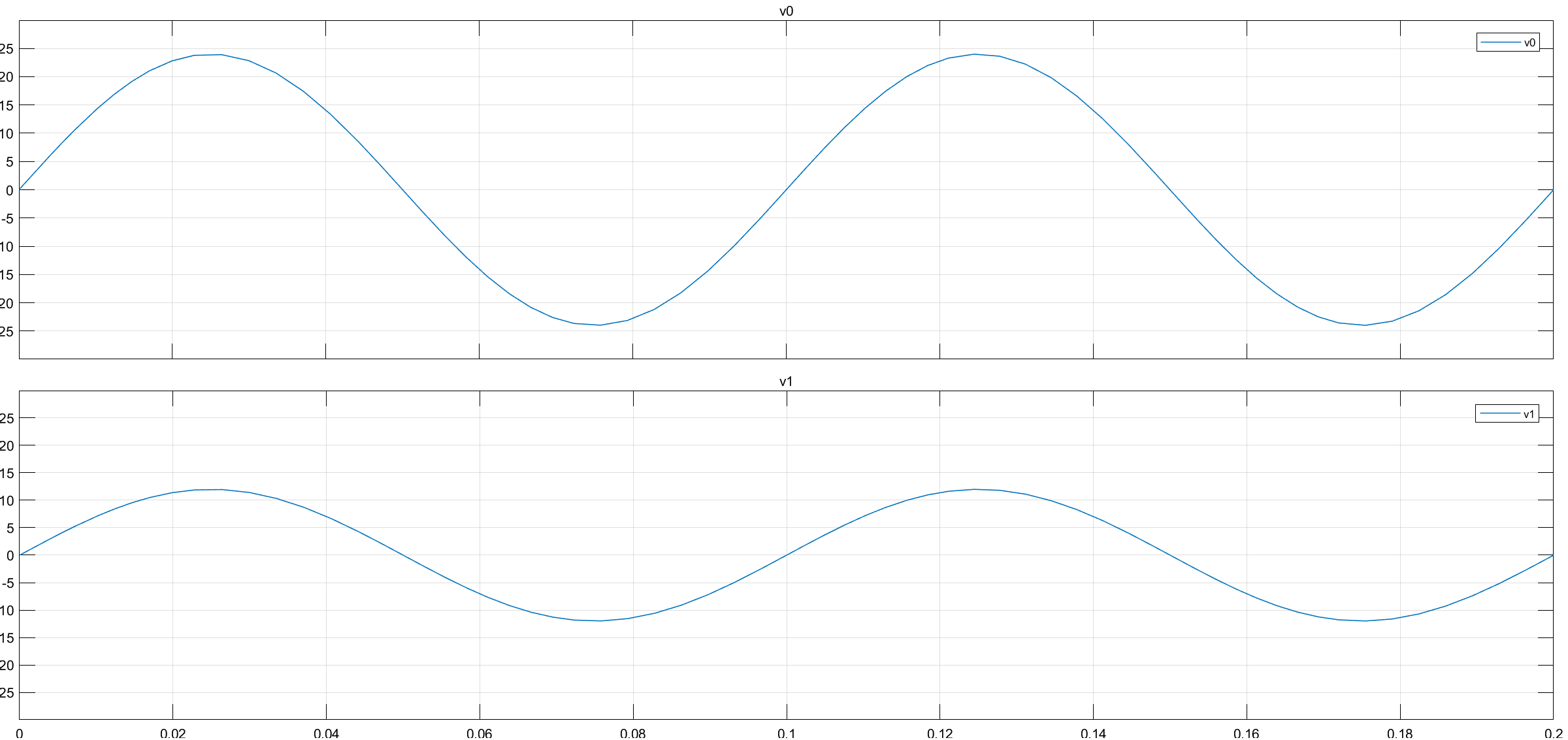
输入电压(v1)幅值12V，输出电压(v0)幅值24V.

β=1/3的OP放大器模型

文件：Op002.slx

反馈回路上，\(R_1=100Ω,R_2=200Ω\)时，\(β=\frac{R_1}{R_1+R_2}=1/3\)

仿真截图略. 此时，输出电压(v0)幅值是输入电压幅值(v1)的3倍

反相放大电路模型

反相放大电路原理如下图. OP放大器输入端极性与前面相反，同相输入端（+）接地.

img

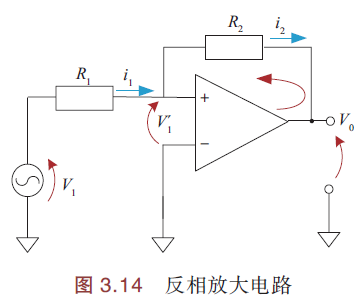
其中，

  • V1：输入电压；
  • V0：输出电压；
  • V1'：输入差分电压

OP放大器内阻极大，反相输入端电流0（虚断），\(i_1\)不流入OP放大器
∴\(i_1=i_2\)
∴

\[\tag{6} \begin{cases} i_1=\frac{V_1-V_1'}{R_1}\\ i_2=\frac{V_1'-V_0}{R_2} \end{cases} \]

此时，工作时OP放大器通信输入端（+）与反相输入端（-）的电位差为0（虚短）. 通信输入端（-）接地时，有
\(V_1'=0\)

\[∵i_1=i_2=\frac{V_1}{R_1}=\frac{-V_0}{R_2}\\ ∴\frac{V_0}{V_1}=-\frac{R_2}{R_1} \tag{7} \]

此时，放大倍数\(\frac{V_0}{V_1}=-\frac{R_2}{R_1}\)

仿真模型：

R1=100Ω，R2=200Ω，停止时间0.2s

img

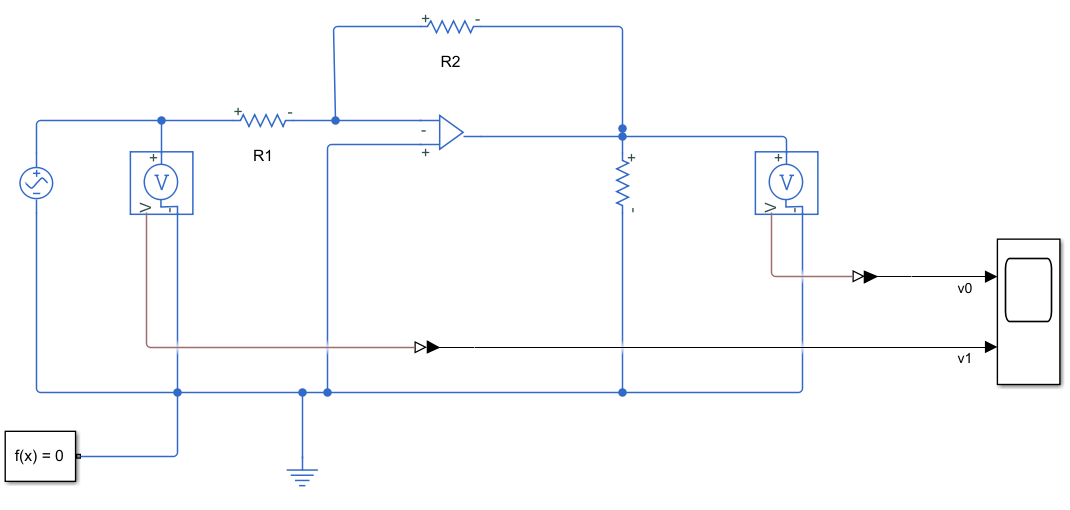
仿真结果：

img

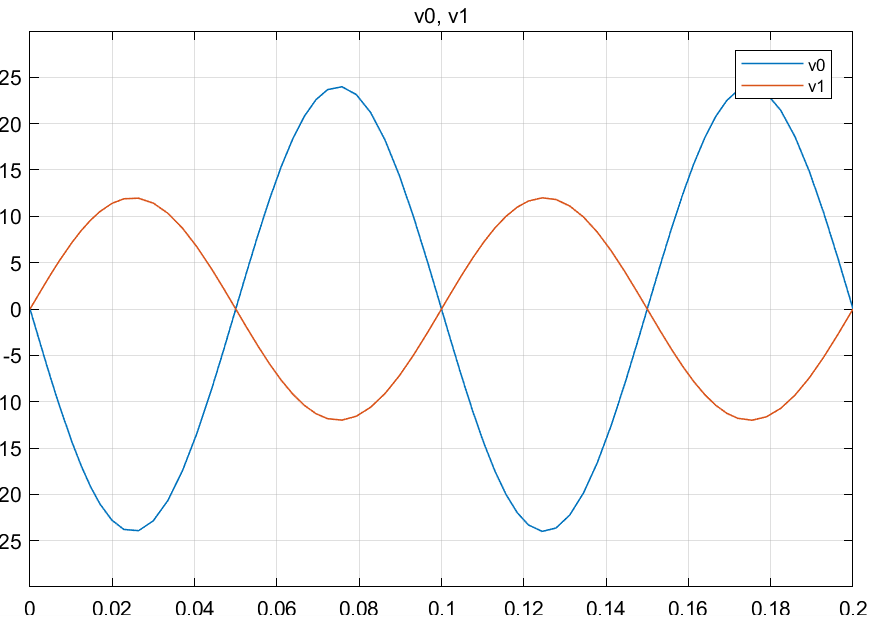
可以看到，输出电压(v0)振幅±24V，输入电压(v1)振幅±12V，振幅翻倍且相位相反. 由此确认反相放大电路功能.

增益和相位差

这部分讲OP放大器放大系数、相位差对应的幅频、相频特性.

增益 <=> 放大系数 <=> 分贝

频率特性、伯德图

向系统输入信号u(t)，会得到输入信号y(t).

系统输入、输出关系：

img

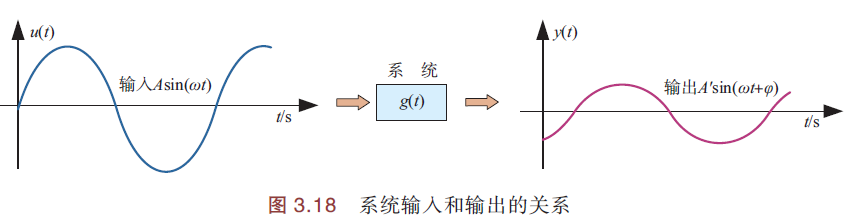
这里的g(t)就是系统的传递函数：\(g(t)=y(t)/u(t)\)

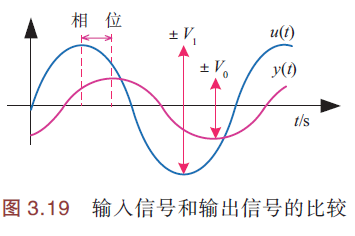
如下图，比较输入、输出信号，可以分析系统特性：

  • 增益 => 幅值变化：输出信号相对于输入信号的增减程度（<=> 放大系数 <=> 传递函数）
  • 相位差：输出信号与输入信号在时间上的偏差

img

伯德图

当系统输入频率变化的信号时，对增益和相位变化特性的分析被称为频率特性分析. 描述这些特性的分析曲线图，被称为伯德图（Bode plot），如下图：

img

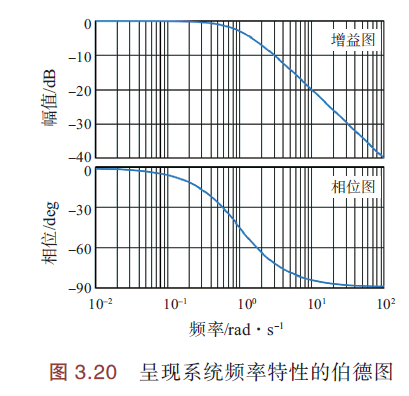
增益、分贝

在伯德图中，增益通常以分贝（decibel，dB）为单位. 分贝是一种对数尺度，用于量化电压、音压等物理量相对于基准值的大小.

使用分贝好处：可以将幅值乘法转换为加法，简化系统的频域分析、理解.

功率、电压、电流的分贝数

功率增益

设基准功率\(P_i\)，目标功率\(P_o\)，则功率增益（dB）：

\[\tag{8} G=10log_{10}\frac{P_o}{P_i} \space [dB] \]

单位分贝（dB），“分”（deci，简写d）表示 1/10；“贝”（bel，简写B）是发明家贝尔名字，1B=10dB

电压增益

根据欧姆定律，

\[\tag{9} V=iR\implies i=\frac{V}{R} \]

功率P：

\[\tag{10} P=Vi=\frac{V^2}{R}=i^2R \]

将(10)代入(8)，可得，

电压增益：

\[\tag{11} G=10log_{10}\frac{P_o}{P_i}=10log_{10}\frac{\frac{V_o^2}{R}}{\frac{V_i^2}{R}}=10log_{10}\Big(\frac{V_o}{V_i}\Big)^2=20log_{10}\frac{V_o}{V_i} \]

电流增益：

\[\tag{12} G=10log_{10}\frac{P_o}{P_i}=10log_{10}\frac{i_o^2R}{i_i^2R}=20log_{10}\frac{i_o}{i_i} \]

例如，前面反相放大电路一节示例中，\(\frac{V_0}{V_1}=-\frac{R_2}{R_1}=-2\). 那么，电压增益：

\[\tag{13} G=20log_{10}\frac{V_o}{V_i}=20log_{10}|\frac{V_0}{V_1}|=20log_{10}2=6.02(dB) \]

∴电压放大2倍 <=> 增益6.02dB

一些常见放大系数与增益对应关系：

img

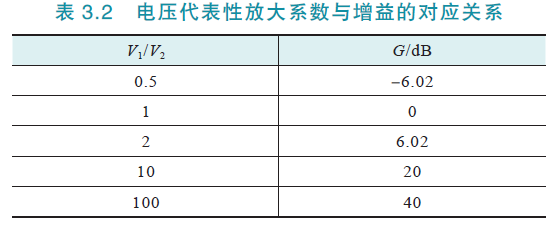
频率、滤波器

电容、电感

电容、电感是滤波基本元件. 如下图，连接交流电压时，电感、电容的阻抗Z（Ω）随交流电压的频率变化而变化.

img

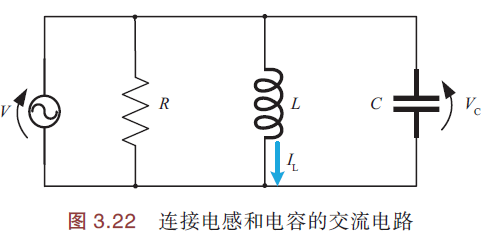
电感L的阻抗\(Z_L\)随着频率升高而增大：

\[\tag{14} Z_L=jωL=j2πfL \]

电容C的阻抗\(Z_C\)随着频率升高而减小：

\[\tag{15} Z_C=\frac{1}{jωC}=\frac{1}{j2πfC} \]

电感的阻抗

电路分析中，常设电流\(i(t)=Ie^{jωt}\)

由电感定义，感应电压\(v=L\frac{di}{dt}\)

∴

\[\tag{16} v(t) = L\frac{di(t)}{dt} = LIjωe^{jωt} = Ljωi(t) = Z_Li(t) \]

\[\tag{17} Z_L=Ljω \]

电容的阻抗

由电容定义，\(C=\frac{Q}{V}\)
由电流定义，\(I_C=\frac{dQ}{dt}=C\frac{dV_c}{dt}\)

∵电荷、电压随时间t变化
∴\(q(t)=Cv(t)\)

电容阻抗与频率成反比，证明：

\[i(t)=Ie^{jωt}\\ \frac{dq(t)}{dt}=C\frac{dv(t)}{dt}=i(t) \]

∴

\[\tag{18} \begin{split} v(t) &= \frac{1}{C}\int_0^t i(t)dt=\frac{1}{C}\int_0^t Ie^{jωt}dt \\ &=\frac{1}{jωC}I\int_0^t e^{jωt}d(jωt) \\ &=\frac{1}{jωC}I\Big[e^{jωt} \Big]_0^t \\ &=\frac{1}{jωC}I\Big(e^{jωt} - 1\Big) \\ &=\frac{1}{jωC}\Big[i(t)- I \Big] \end{split} \]

\[\tag{19} Z_C=\frac{1}{jωC} \]

阻抗的模型设计

对电容、低昂那的阻抗进行模型设计，研究阻抗与频率的关系.

由于要分析频率特性，因此以频率为横轴，观察电容、电感的阻抗（纵轴）.

  • 电感L：30mH
  • 电容C：500uF
  • 频率f：1~1000Hz

涉及的频率有3种形式：

1）角频率：\(1 rad/s=1/2πHz\)；
2）频率f：\(1Hz=1s^{-1}=2π rad/s\)；
3）转速N：\(1 rpm=1r/min=1min^{-1}=1/60s^{-1}=1/60Hz\)

其中，\(ω=2πf (rad/s)\)

文件名：impedance.slx

所用模块：

img

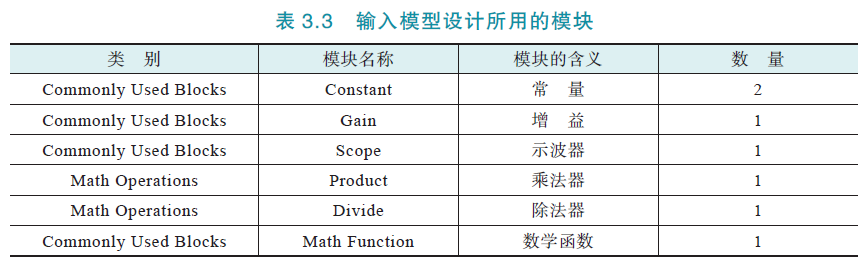
仿真模型：

img
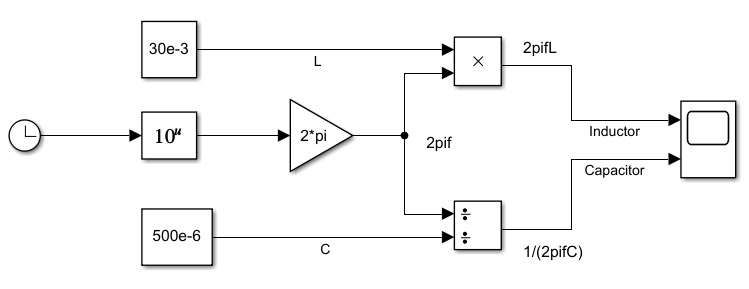
其中，
L：Constant参数为30e-3（30mH）
C：Constant参数为500e-6（500uF）
ω：Gain增益为2*pi（ω=2πf）
除法：Divide输入数为//
停止时间设为3s

仿真结果：

img
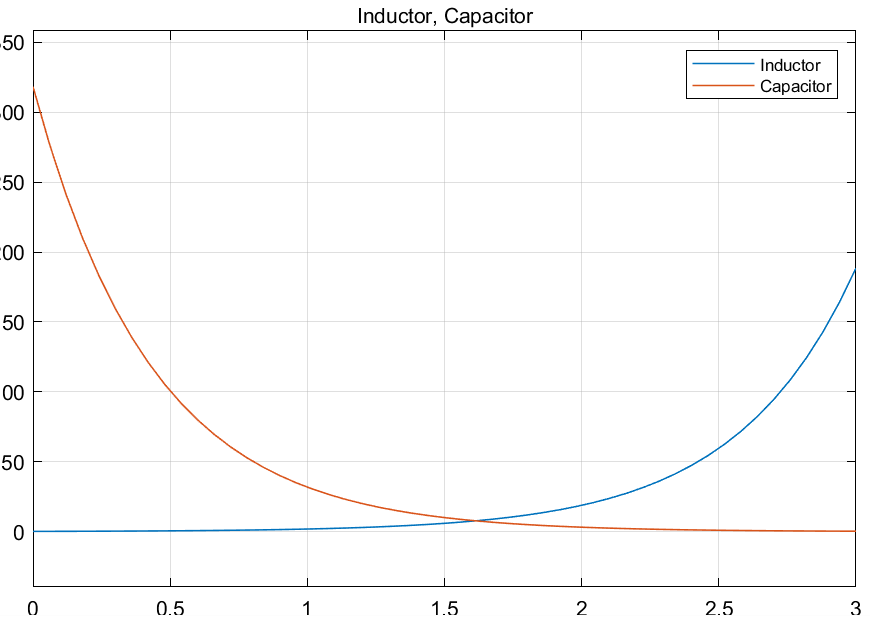
其中，横轴代表频率，可以表示频率f范围：1~1000Hz，如2，对应频率\(10^2=100Hz\)

可以看出，频率越高，电感的阻抗越高，电容的阻抗越低

滤波器种类

  1. 无源滤波器

又称LC滤波器，由电阻、电感、电容的无源元件组成. 这类滤波器不具备增益能力，即无法对信号进行放大. 将电感与电容串联形成低阻抗旁路，能对主要次谐波（如3次、5次、7次谐波）进行滤波.

常见无源滤波器：单调谐滤波器、双调谐滤波器、高通滤波器.

无源滤波器能有效滤除特定谐波成分，伯德图如下图：

img

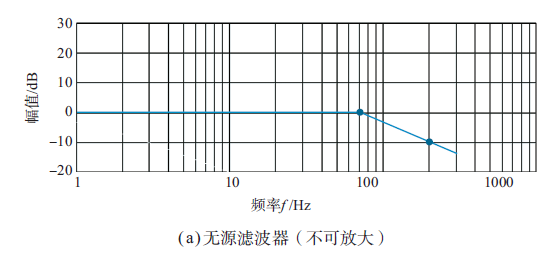
无源滤波器的频率响应曲线通常不平坦，实际中常级联不同阶数的滤波电路来改善效果

  1. 有源滤波器

在无源滤波器基础上，添加了OP放大器等有源元件，其输出信号的增益可以远大于1.

有源滤波器的频率响应曲线较平坦，可调整放大系数实现不同的滤波特性. 结合OP放大器高输入阻抗和低输出阻抗的特点，可以有效避免负载引起的信号衰减，获得更高的通信质量.

伯德图如下：

img

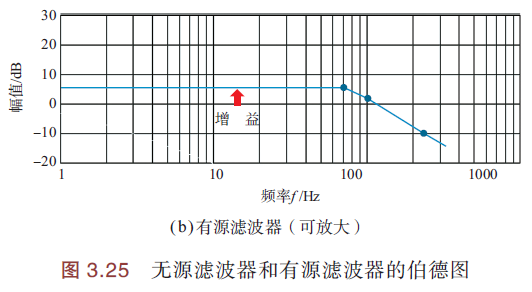
无源滤波器的模型设计

需要用Simscope.

原理

使用电阻、电容搭建的无源低通滤波器电路，如下图：

img

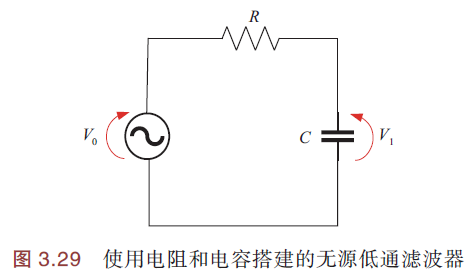
幅频特性，如下图：

img

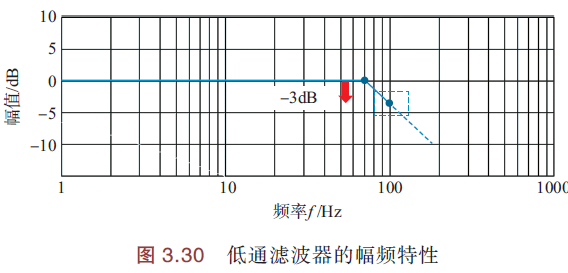
当截止频率\(f_C=100Hz\)时，频率<100Hz的信号可以通过，>100Hz的信号无法通过.

增益=0dB，表示输入对应输出的放大系数为1 => 无源滤波器没有信号放大功能，只有衰减功能.

输入电压\(V_0\)与输出电压\(V_1\)有分压关系，如下图(a). 电路中电阻R等效阻抗\(Z_R\)，电容C等效阻抗\(Z_C\)，如下图(b).

等效阻容电路：

img

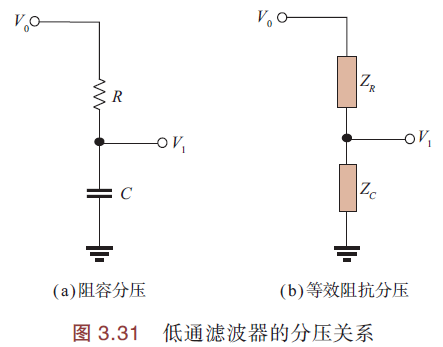
电阻、电容串联，流过的电流i相等. 由欧姆定律，

\[V_0=i(Z_R+Z_C)\\ V_1=iZ_C \]

放大系数G：

\[\frac{V_1}{V_0}=\frac{iZ_C}{i(Z_R+Z_C)}=\frac{Z_C}{Z_R+Z_C} \]

设输入电压\(V_0\)是频率的函数：\(V_0=Ve^{jωt}\)

因为电容阻抗不是固定值，而是取决于输入电压频率，所以放大系数G取决于输入电压频率：

\[\tag{20} \begin{split} G(jω) &=\frac{Z_C}{Z_R+Z_C}=\frac{\frac{1}{jωC}}{R+\frac{1}{jωC}}=\frac{1}{1+jωRC}\\ &=\frac{1-jωRC}{(1+jωRC)(1-jωRC)}=\frac{1-jωRC}{1+(ωRC)^2} \end{split} \]

增益是放大系数的绝对值，即\(|G(jω)|\)，但包含虚数，如何求模？

对于复数\(Z=a+bi\)，模长\(|Z|=\sqrt {a^2+b^2}\)
∴

\[\tag{21} \begin{split} |G(jω)| &= \sqrt{\Big[\frac{1}{1+(ωRC)^2} \Big]^2 + \Big[\frac{-ωRC}{1+(ωRC)^2} \Big]^2} \\ &= \sqrt{\frac{1+(ωRC)^2}{[1+(ωRC)^2]^2}} \\ &= \frac{1}{\sqrt{1+(ωRC)^2}} \end{split} \]

可知，\(ω\)⬆，增益⬇；\(ω=0\)时，增益\(20log_{10}|G(jω)|=0\)

下面求截止频率\(ω_C\). \(ω_C\)为\(ω=0\)时增益（0dB）下降3dB对应的频率，设\(ω=ω_C\)，则

\[\begin{aligned} 20log_{10}|G(jω_C)| &= 0-3 \\ log_{10}|G(jω_C)| &= \frac{-3}{20} \\ |G(jω_C)| &= 10^{\frac{-3}{20}} ≈ 0.7079 \\ ∴ \frac{1}{\sqrt{1+(ω_CRC)^2}} &= 0.7079\\ \frac{1}{1+(ω_CRC)^2} &= 0.7079^2 ≈ \frac{1}{2} \\ ω_CRC &= 1 \\ ω_C &= 2πf=\frac{1}{RC} \tag{22} \end{aligned} \]

∴

\[\tag{23} f=\frac{1}{2πRC} \]

注意：增益-3dB，意味着功率减半，电压衰减为原来的\(1/\sqrt 2\).

再看相位θ，根据(20)，放大系数G(jω)是一个复数，由实部、虚部组成.

如下图，对于复数\(z=a+bi\)，有

\[tanθ=\frac{b}{a}\\ \implies θ=tan^{-1}\frac{b}{a} \]

对于\(G(jω)\)，

\[\tag{24} \begin{aligned} a &=\frac{1}{1+(ωRC)^2},b=\frac{-ωRC}{1+(ωRC)^2}\\ θ &=tan^{-1}\frac{b}{a}=\frac{-ωRC}{1}=tan^{-1}(-ωRC)\\ \end{aligned} \]

img

模型设计

低通滤波器的设计方法：根据截止频率\(f_C\)确定R、C，再根据设计要求使用Simscape设计模型.

设计要求：

  • 滤波器类别：无源低通滤波器
  • 截止频率：\(f_C=100Hz\)
  • 电源电压：AC幅值12V
  • 电阻：R=100Ω

由(23)，电容：

\[C=\frac{1}{2πRf}=\frac{1}{2π*100*100}=16 μF \]

文件：passiveLow.slx

所用模块：

img

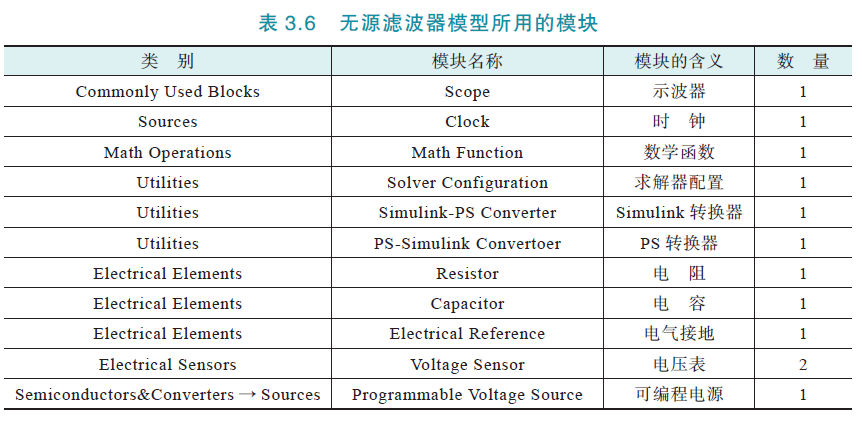
仿真模型：

img

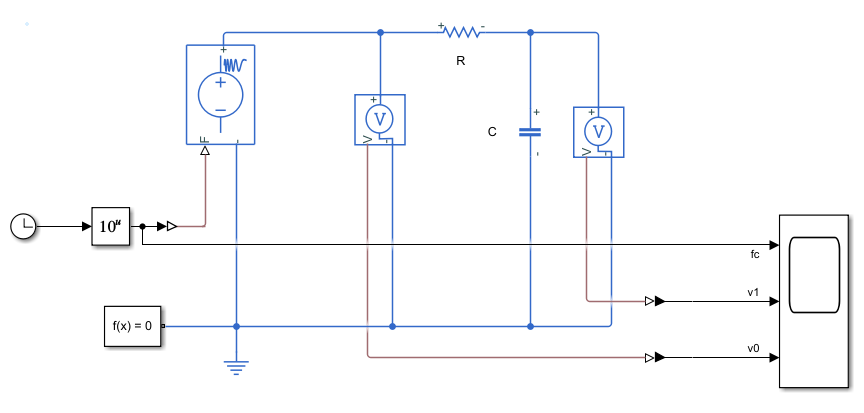
其中，可编程电源AC voltage peak magnitude（电压幅值）设为12V，AC frquency configuration（频率配置）设为“External”；停止时间3s

注意：放大系数\(G(jω)\)是随\(ω\)变化的函数，不是t的函数. 滤波器\(RC\)控制了截止频率处放大系数的增益\(G(jω)\)；图中Clock模块，用于产生变频电压信号，输入低通无源滤波器模型.

模型中，\(f(t)=10^t Hz, ω(t)=2πf(t) (rad/s)\).
∵停止时间3s
∴频率\(f(t)=1...10^3Hz\)

仿真结果：

img

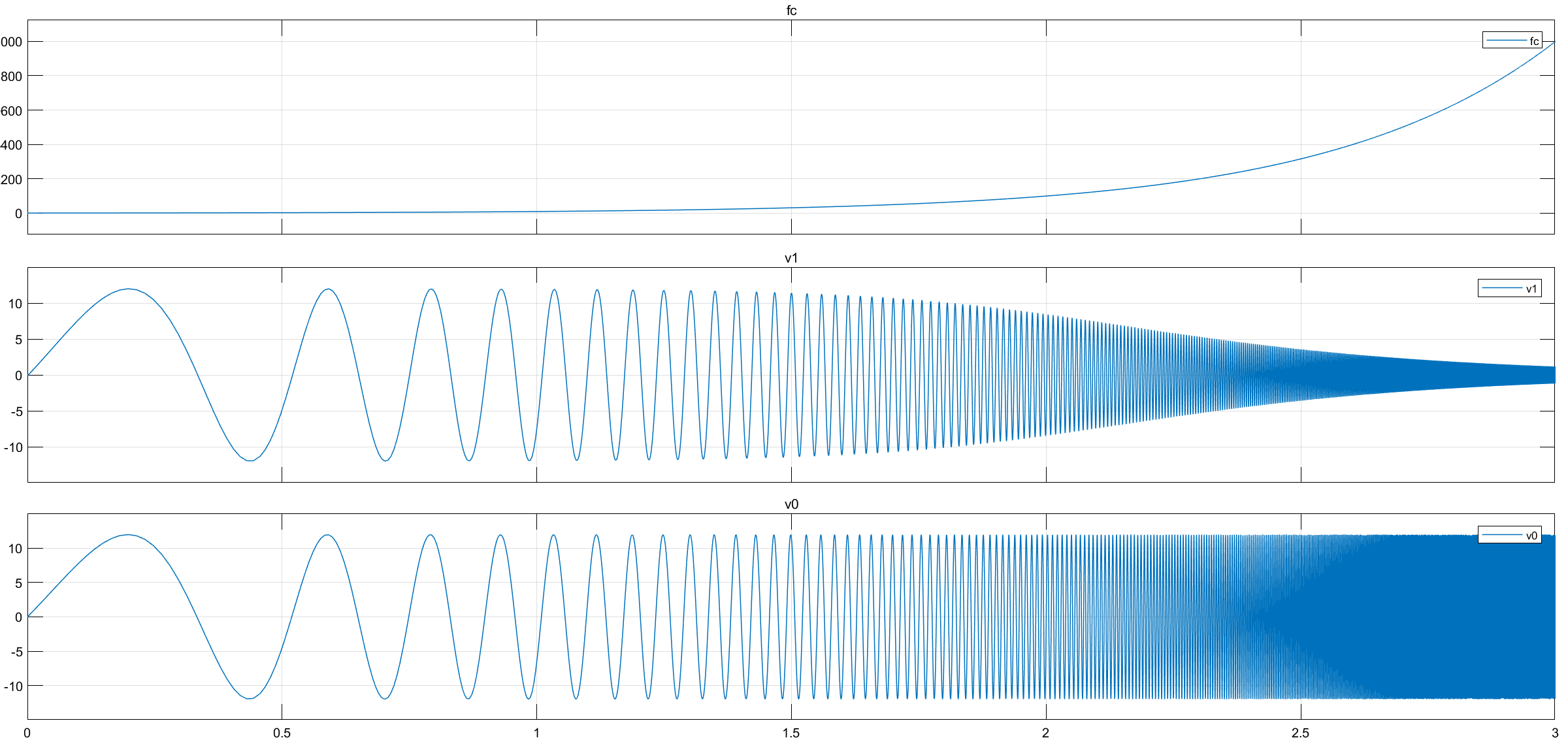
横轴都是\(t(s)\)，第1行曲线表示输入频率f(t)随时间变化；第2行、第3行表示输出电压V1波形、输入电压V0波形.

当t=2s时，\(f(t)=10^2=100Hz\)，输出\(V_1(f=100Hz)\)，输入\(V_0(f=100Hz)\)

从结果可知，截止频率\(f(2)=100Hz\)时（与前面幅频特性保持一致），输出电压V1 < 输入电压V0=12V

由(24)，相位：

\[\begin{split} θ &= tan^{-1}(-ω_CRC)=tan^{-1}(-2πf_CRC) \\ &= tan^{-1}(-2π*100*100*16*10^{-6}) \\ &=tan^{-1}(-1)=-\frac{π}{4} (rad) \end{split} \]

理论上，说明在截止频率\(f_C\)处，相位延迟π/4 rad （45°）

如何确认模型是否满足设计要求？

确认截止频率\(f_C\)处是否满足设计要求：
1）增益：-3dB
2）相位：延迟π/4 rad

使用Scope模块自带测量工具进行测量，类似于真实示波器的测量.

需要设置的关键步骤如下图：

img

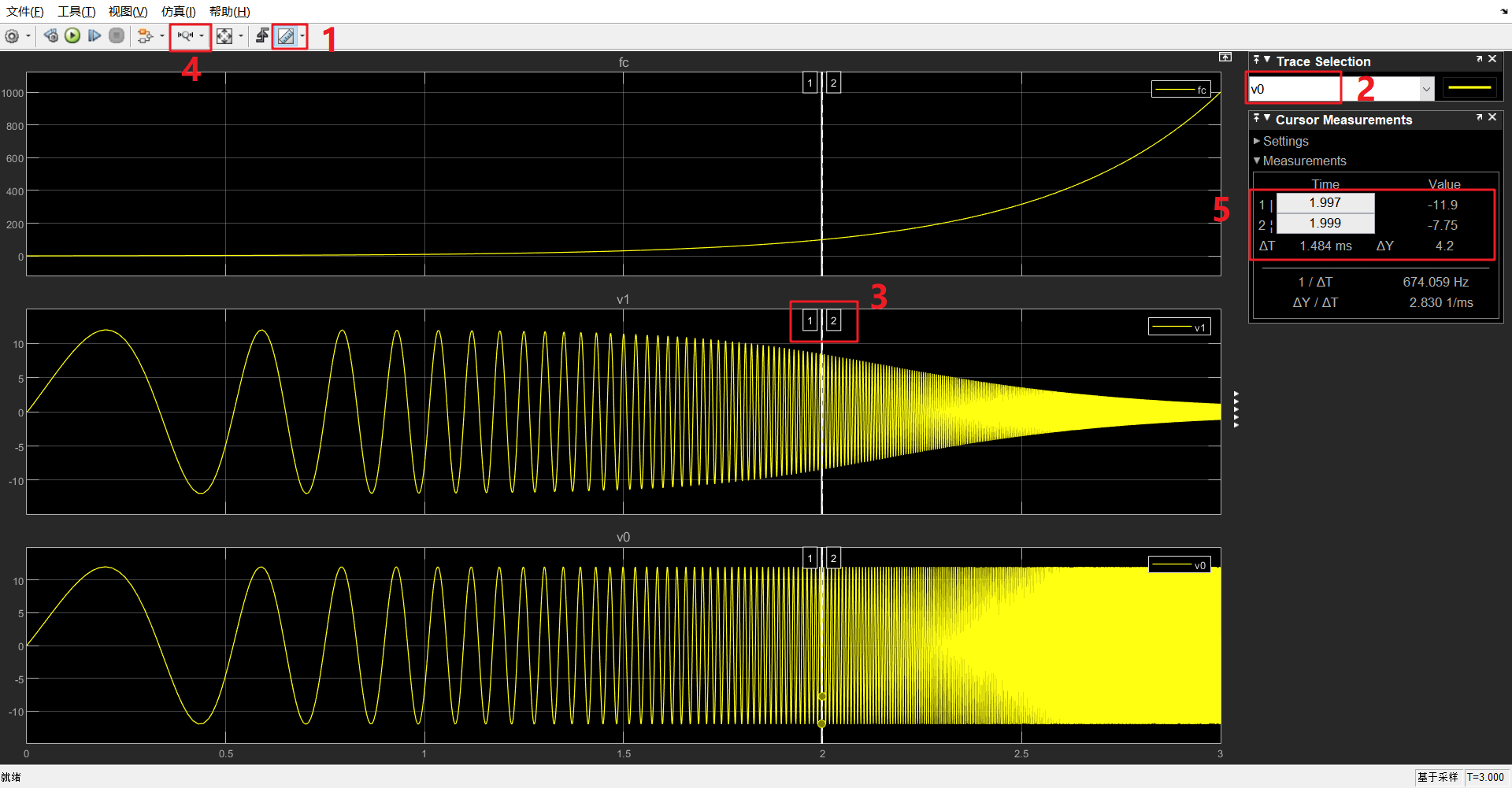
步骤：

  1. 打开测量工具

有2种方式开启测量工具：

1）点击工具栏以下图标（需要matlab r2020b以上版本）：

img

2）勾选菜单 工具> Measurements> Trace Selection, Cursor Measurements

img

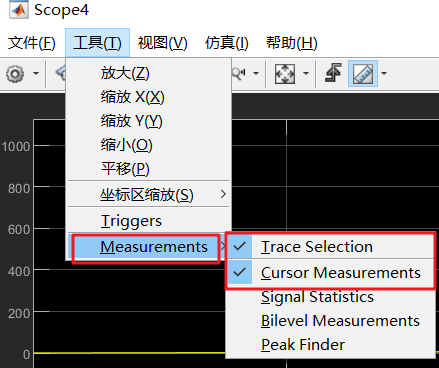
  1. 选择要测量的曲线，选v0或v1（每次测量一个曲线）

  2. 调节竖线，位于要测量的点t=2s附近即可，对应频率\(f(t)=10^2Hz=100Hz\)即截止频率\(f_C\)

关键是要测量附近的极值点，获取电压幅值，从而求得增益

  1. 缩放x轴，缩小要查看的区间

  2. 读取测量点电压极值，即为电压曲线幅值

如下图，分别读取到输入v0极小值-11.9V，输出v1极小值-8.4V，时间差Δt=1.484ms.
∴增益：\(20*log10(-8.4/-11.9)=-3.0254dB\)，满足设计要求-3dB.

img

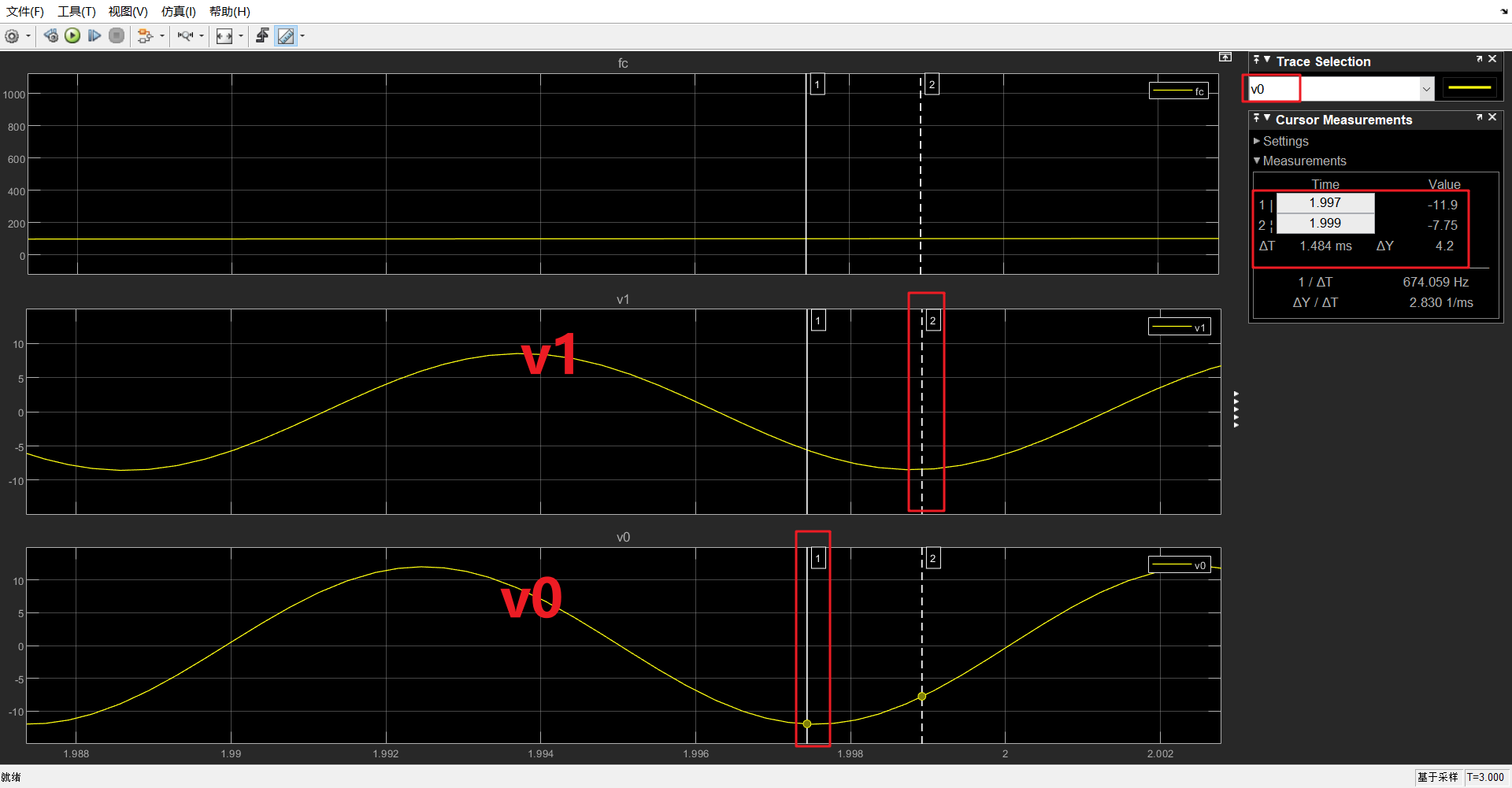
接下来确认相位.
v0、v1取得极小值时间差Δt=1.484ms
设计要求（理论值）：π/4 rad = π/4 / (2π) = 1/8周
理论相位差对应时间：\(1/8 * 1/f_C = 1/8 * 1/100 s = 1.25ms≈Δt\)
由于测量存在一定误差，所以可以认为满足相位要求

有源滤波器的模型设计

无源滤波器只能衰减不需要的频段，有源滤波器可以放大需要的频段.

设计要求

使用Simscape设计模型

  • 滤波器类别：低通滤波器
  • 截止频率：\(f_C=100Hz\)
  • 增益：6dB
  • 电源电压：AC 12V

电路设计

下面组合放大器、无源元件设计有源低通滤波器的模型

放大功能采用反相放大电路模型小节中的反相放大电路. 反向放大电路的放大系数取决于模型中R1、R2的比值：
由(7)，

\[\frac{V_0}{V_1}=-\frac{R_2}{R_1} \]

设计要求增益6dB：

\[20log_{10}x=6\\ x=10^{\frac{6}{20}}=2.0 \]

其中，x代表放大系数，即\(|V_0/V_1|\)

设R2=200Ω，则R1=100Ω
电容：\(f=\frac{1}{2πRC}\implies C=\frac{1}{2πfR}=\frac{1}{2π*100*200}=8*10^{-6}F\)

模型设计

文件名：activeLow.slx

R1：100Ω；R2：200Ω；C：8μF；
停止时间3s（频率100Hz，对应时间点t=2s）

在无源滤波器模型基础上，添加：

img

仿真模型：

img

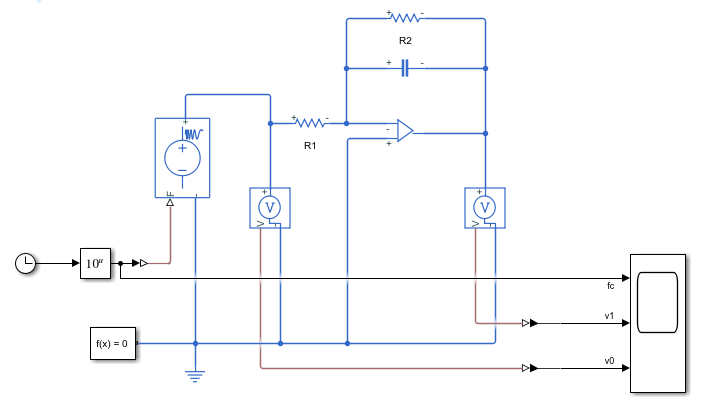
频率\(10Hz\)时，周期0.1s，电压从V1=12V放大到V0=23.8V，
增益：\(20*log10(23.8/11.9)=6.0206 dB\)
相位滞后：实测\(Δt=57.929ms\)，约\(Δt/T=57.929ms/0.1s=0.57929\)个周期

img

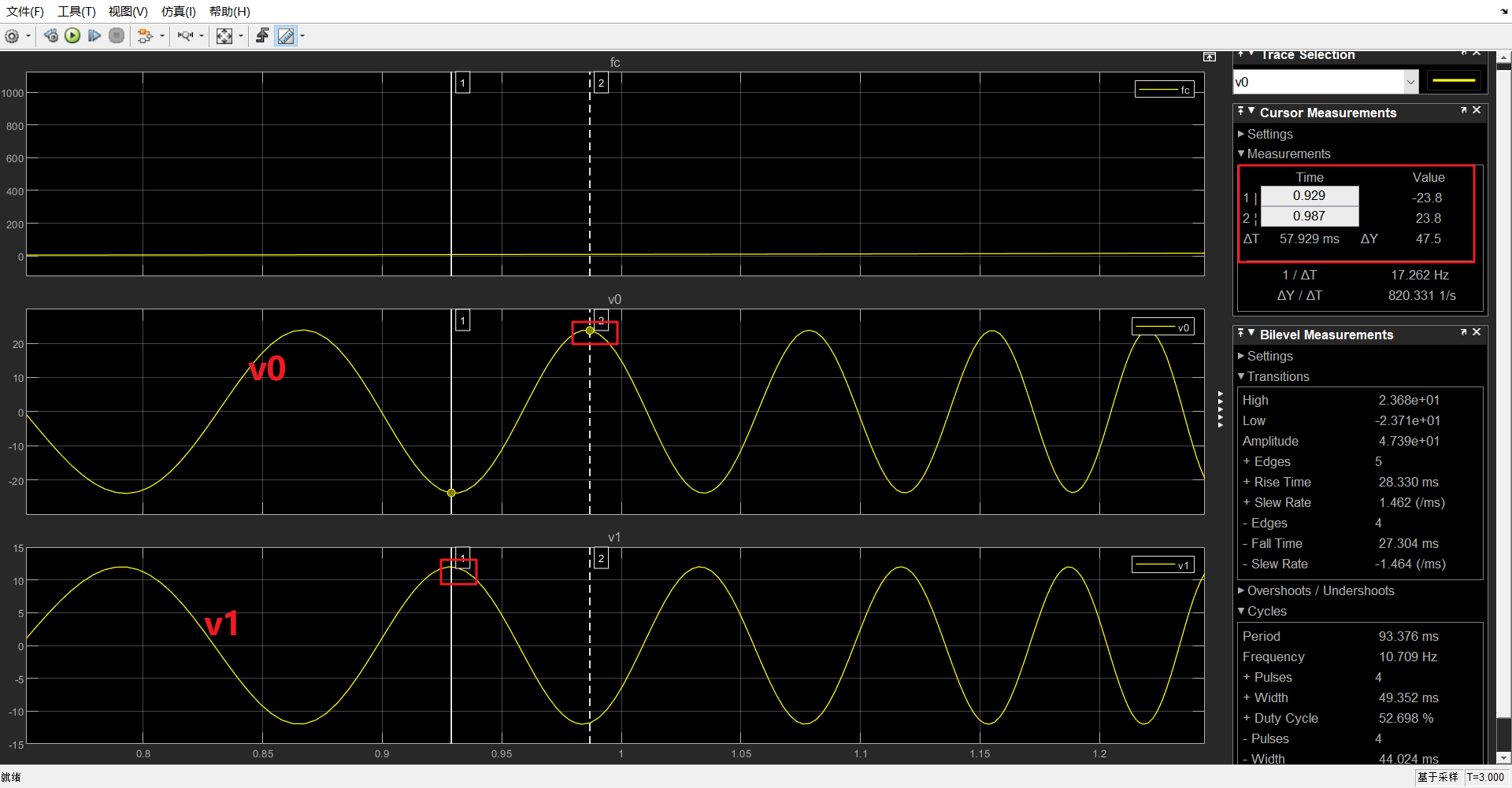
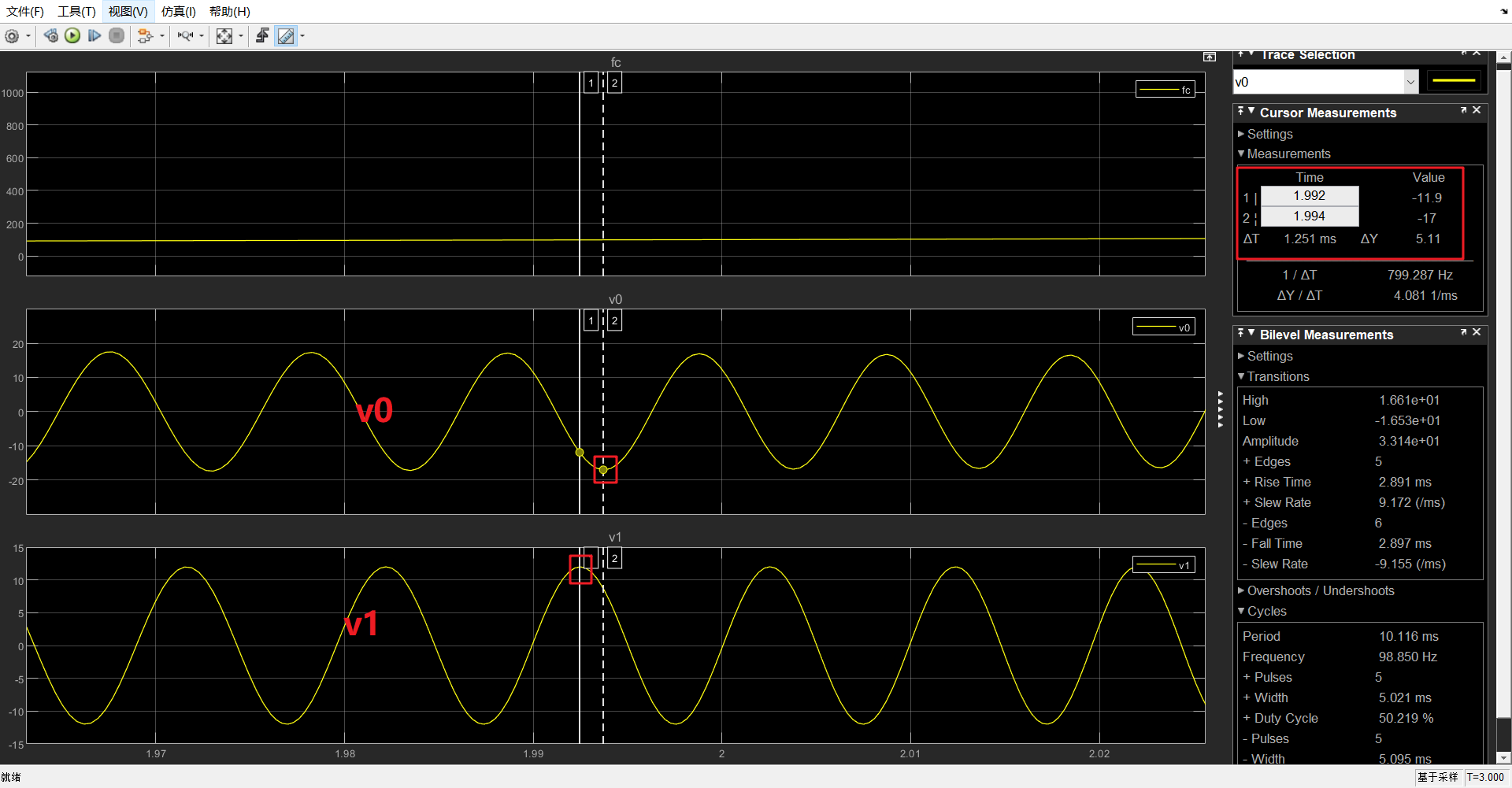
在截止频率\(f_C=100Hz\)处，周期0.01s，电压从V1=12V反相放大到V0=-17.0V，
增益：\(-20*log10(17.0/12)=-3.0254 dB\)(负号表示反相)，
相位差\(θ\)理论值：

\[\begin{split} θ &= tan^{-1}(-2πfRC)=tan^{-1}(2π*100*200*8*10^{-6}) \\ &= tan^{-1}(-1)=-\frac{π}{4} (rad) \end{split} \]

即相位滞后\(1/8\)圆周，即\(0.01*1/8s=1.25ms\)

注意：因为滞后1/8圆周，所以我们考察V1幅值延时约1/8圆周位置

实测值（见下图Δt）为1.251ms，符合要求

img

参考

[1] 武超. MBD入门: 无刷电机控制代码生成. 科学出版社. 2025.1
[2] 电路基础：电感
[3] 电路基础：电容器

posted @ 2025-08-05 21:18  明明1109  阅读(142)  评论(0)    收藏  举报