电路基础：电感

目录

• 电感
  • 电磁感应
  • 电感器
    • 基本性质
    • 充磁
    • 去磁
  • 电感方程
  • 电感器的能量
  • LR充电电路
  • LR放电电路
  • 开关转换引起的尖峰电压
  • 直导线电感
  • 电感的串联、并联
  • 感抗
  • 实际电感模型
• 参考

电感

电磁感应

电子学三个基本元件：电阻、电容、电感.

电容器以电场方式存储电能，电感以磁场方式存储电能.

电感性

当导线中有电流流过时，导线周围会产生磁场. 增大或减小导线中电流值，磁场强度随之增大或减小. 在磁场强度的变化过程中，出现的这种现象称为感应现象，电感性是电路的一种性质.

电感性，类似于电阻性、电容性，但是不生成热，也不存储电荷，仅与磁场相关.

电感反映了电路中电流、电压的变化，而电流、电压的变化是由于自由电子受力的作用引起磁场变化的结果.

电感效应，类似于电容器，只有在外加电压会电流随时间增大或减小的变化过程中才会产生，而电阻与时间无关.

电感器

电感器（简称电感），一种专门设计为有效利用电磁感应现象的设备. 内部可产生很大的集中的磁通量，当电流变化较大时，可承受住较大的自感电压.

注：导线也存在自感，不过较小，通常忽略.

电感一般具有环状结构，下图从左到右，分别是螺线管、环形螺线管、螺旋形导线：

空心电感图形符号：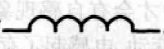

磁心式电感、可调芯式电感器、铁氧体磁环的结构和相应图形符号：

磁心电感产生的磁场强度比空心电感器的要大得多，因为绕在磁芯上的线圈产生磁场作用于磁心材料内部的原子使其磁化，所以磁心电感器的自感比空心电感的自感大.

一句话：在电感器内，放置磁心，只需要很少的线圈匝数，就能得到所需的电感值.

基本性质

电感器作用类似于时变电流灵敏电阻：只有当电流变化时，电感才起到“阻碍”作用；在直流稳态条件下，相当于一根传输电流的导线.（电感性）

注：时变电路，指大小或方向随时间变化的电流，区别于恒定电流.

当外加电压增大时，电感的作用相当于时变电阻，在电流随时间快速增大时，阻值达到最大；
当外加电压减小时，电感相当于时变的电压源（或负电阻），它会维持电流的流动，当电流随时间快速减小时，其电压值最大.

如下图(a)，电感两端所加电压值增大时，电路中电流将增加，通过螺线管线圈的磁通量增大，增大的磁通量产生作用在自由电子上的反向作用力，该反向力就是与电源电源方向相反的感应EMF（感应电动势），称为反向感应EMF.
反向感应EMF起到阻碍电流突然增大的作用.

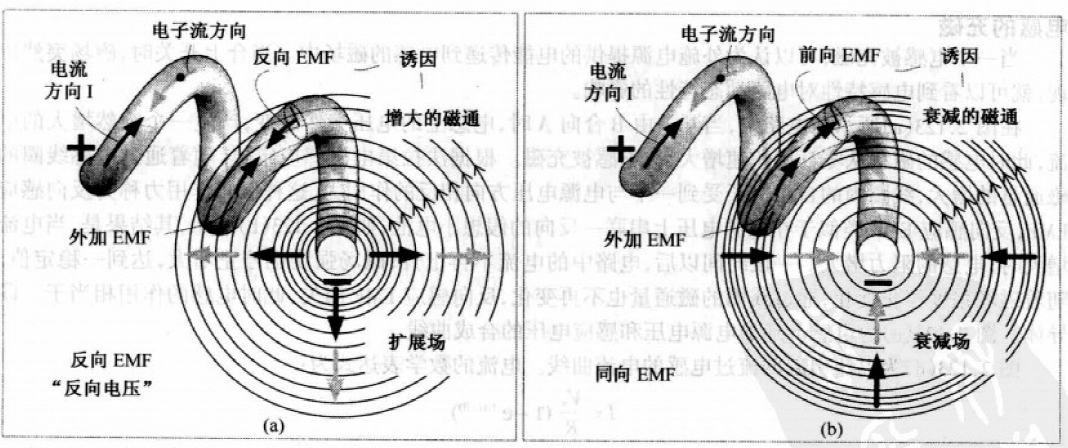
如图(b)，电感两端所加电压值减小时，电路中电流将减小，通过螺线管线圈的磁通量减小，减小的磁通量产生作用在自由电子上的同向作用力，该同向力是与突变前的外加电压同相的感应EMF，称为同向感应EMF.
同向感应EMF作用是阻碍电流突然变小.

充磁

电感的充磁：将电能转换成电感中的磁场能量的过程.

如下图(a)，当开关由B合向A时，电感电压突然改变，产生突然增大的电流，此时，电感的磁场从0开始快速增大，称电感被充磁.

根据法拉第电磁感应定律，随着通过通电线圈的磁通量增大，线圈内的自由电子受到一个与电源电压方向相反的作用力，这种反向作用力称为反向感应EMF.

如下图(b)，当电流⬆，电感的阻力⬆；当电流停止⬆，磁场强度也停止⬆，达到稳定值. 磁场强度停止变化 => 通过线圈的磁通量不变，反向感应EMF消失. 此时，电感 = 导体

注：⬆=增大

电感充磁过程：

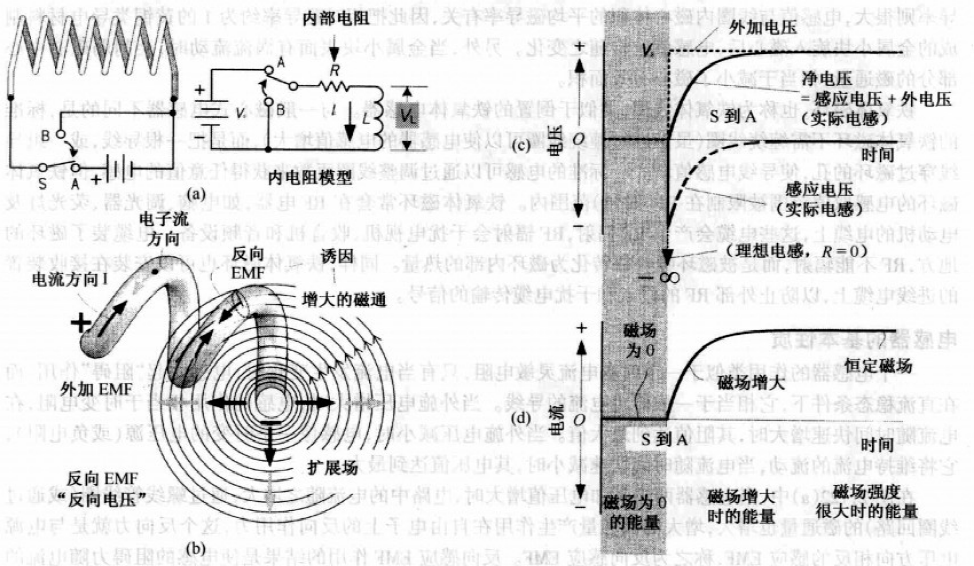
图(c)是电感外加电源电压和感应电压的合成曲线.
图(d)是电压引起的流过电感引起的电流曲线. 电流表达式：\(I=\frac{V_S}{R}(1-e^{-t/(L/R)})\)
注：R是电感内阻

从不同角度看充磁过程：

• 从能量角度看，电能 → 磁场能；
• 从功率角度看，电压降是能量注入磁场的结果

去磁

电感的去磁，就是把电感中的磁场能量释放回电路转换成电能的过程.

如下图(a)，当开关由A合向B时，电感两端电压突然改变，使得电流趋于0，电感线圈的磁场强度骤然减小，但是，电感阻碍磁场的减小.

根据法拉第电磁感应定律，通过线圈的磁通量⬇，线圈内自由电子受到一个与开关动作前的电源电压同向的作用力，称为同向感应EMF.

如图(b)，电感失去的磁场能量释放到电路中，转化为电场能量.

图(c)是电感上外加电源电压和感应电压的合成曲线
图(d)是电感上的合成电压引起的流过电感的电流曲线. 电流数学表达式：\(I=\frac{V_S}{R}e^{-t/(L/R)}\)

电感方程

感应电压（反向或同向）的赋值正比于电感电流的变化率或磁通量的变化率.

感应电压和电流关系：

\[V_L=L\frac{dI_L}{dt} \]

左边是感应电压，右边是感应电流的变化率

两边求积分，可得感应电流：

\[I_L= \frac{1}{L} \int V_Ldt \]

其中，L称为电感系数（单位：亨利，H），1H = 电流变化率为1A/s时1V感应电压，即：

\[1H=\frac{1V}{1A/s} \]

电容器基本由制造商制作，但电感器常自制. 一些典型商用电感器：

电感器的能量

理想电感器同理想电容器，不消耗能量，将能量存储在磁场中，当磁场减少时，又将能量释放回电路中.

功率定理\(P=IV\) + 功率定义\(P=dW/dt\) + 电感方程\(V=LdI/dt\)，并用电感储能\(E_L\)代替\(W\)，可得，

\[E_L=W=\int Pdt=\int IVdt=\int ILdI=\frac{1}{2}LI^2 \]

其中，\(E_L\)能量（单位：J），I电流（单位：A），L电感（单位：H）

实际电路中，少部分能量会被内阻消耗，转化为热能.

LR充电电路

电场能量 \(\to\) 磁场能量

当电阻与电感串联时，电阻控制着输入电感磁场中能量的变化速率. 当磁场减少时，电阻也控制着能量释放回电路的速率.

下图(a)，是由直流电源、开关组成的RL电路. 开关闭合瞬间t=0，(b)是电压、电流的响应曲线：

注：R=100Ω, L=20mH, \(V_S=10V\)

RL充电电路的电流及电压公式：

\[I=\frac{V_S}{R}(1-e^{-t/(L/R)})\iff \frac{t}{L/R}=-ln(\frac{I-V_S/R}{V_S})\\ V_R=IR=V_S(1-e^{-t/(L/R)})\iff \frac{t}{L/R}=-ln(\frac{V_R-V_S}{V_S})\\ V_L=L\frac{dI}{dt}=V_Se^{-t/(L/R)}\iff \frac{t}{L/R}=-ln(\frac{V_L}{V_S}) \]

时间常数τ=L/R, e=2.718

对闭合回路，应用基尔霍夫电压定律，RL电路的充电响应：

\[V_S=IR+L\frac{dI}{dt} \]

转换为标准形式：

\[\frac{dI}{dt}+\frac{R}{L}I=\frac{V_S}{L} \]

如何求出电流？

初始条件：开关闭合前电流\(I(0)=0\)
可根据前面求\(I\)的公式，也可以解上面的线性一阶非齐次微分方程，可解得电流：

\[I=\frac{V_S}{R}(1-e^{t/(L/R)}) \]

∴电阻电压：

\[V_R=IR=V_S(1-e^{t/(L/R)}) \]

电感电压：

\[V_L=L\frac{dI}{dt}=V_Se^{-t/(L/R)} \]

LR放电电路

磁场能量 $\to $ 电场能量

当断开开关，断开电源后，电容器可以以电场的形式存储能量. 但电感无法保存电荷，电感的磁场会随着电流的减少而消失，存储其中的磁场会转化为电能释放回电路.

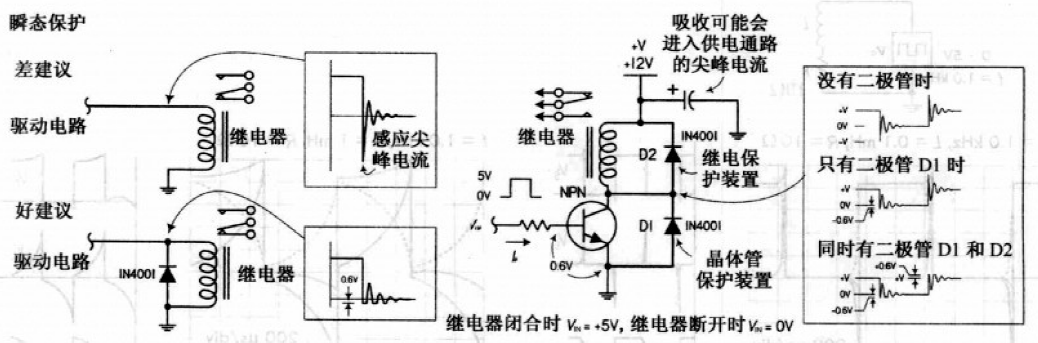
开关断开时，由于感应电压 ∝ 磁场变化率，所以磁场骤降引起的感应电压比电源电压大得多；开关断开瞬间，开关触点通常产生火花或电弧，如下图(a).

如果电感系数、电流过大时，短时间释放能量很大，可能导致开关触头被熔化. 如果在开关触头两端连接串联的电容和电阻，则可抑制火花或电弧. 这样的RC组合，称为缓冲网络（下图的减震器）.

大电感负载连接晶体管开关，如继电器、螺线管，就需要进行保护.

对RL放电电路，应用基尔霍夫电压定律，对闭合回路的电压取和：

\[V_S=IR+L\frac{dI}{dt} \]

转换成标准形：

\[\frac{dI}{dt}+\frac{R}{L}I=\frac{V}{L} \]

初始条件：开关断开前的电流\(I(0)=V_R/R\)

可用前面的公式，或解上面线性一阶非齐次微分方程：

\[I=\frac{V_S}{R}e^{-t/(L/R)} \]

∴电阻R电压：

\[V_R=IR=V_Se^{-t/(L/R)} \]

L感应电压：

\[V_L=L\frac{dI}{dt}=-V_Se^{-t/(L/R)} \]

图(b)中，设移去电源，开关从A点打到B点接地，电路未断开，则电流、电压表达式：

\[I=\frac{V_S}{R}e^{-t/(L/R)}\iff \frac{t}{L/R}=-ln(\frac{IR}{V_S})\\ V_R=IR=V_Se^{-t/(L/R)}\iff \frac{t}{L/R}=-ln(\frac{V_R}{V_S})\\ V_L=L\frac{dI}{dt}=-V_Se^{-t/(L/R)}\iff \frac{t}{L/R}=-ln(\frac{V_L}{R}) \]

时间常数τ=L/R,e=2.718,\(ln(-1)=πi\),i为虚数

开关转换引起的尖峰电压

大感性负载的电路中，如继电器、螺线管、电动机经由机械开关或晶体管开关导通或断开过程中，常见尖峰状感应电压.
即使电源电压很小，形成的尖峰电压也可能有数百V.

尖峰电压可能引起电弧，导致开关性能降低，或损坏晶体管、其他集成开关设备.

下图电路，将一个二极管（电流单向流动装置）并联至一个继电器线圈两端，需要断开电路时，为感应的尖峰电压提供“电压缓冲”路径.

直导线电感

每个通电导体（不一定绕成线圈）的周围，都会有磁场，因此有自感系数. 如一段直导线有与之相关的电感系数.

因为在给定EMF（感应电动势）作用下，每个定向移动的自由电子产生的磁场的平均效应.

自由空间内，一段非磁性材料的直导线或导体棒的电感为：

\[L=0.00508b\biggm[ln(\frac{2b}{a}-0.75) \biggm] \]

其中，L电感（单位：μH），a导线半径，b导线长度（单位：英尺），ln自然对数

电感的串联、并联

• 串联电感

2个及以上电感串联时，线圈相互分开一段距离，使彼此不在其他线圈的磁场中，则总电感量为各电感量之和：

\[L_{tot}=L_1+L_2+...+L_N \]

串联电感的计算公式，可通过基尔霍夫电压定律求出. 如下图3个电感\(L_1,L_2,L_3\)串联得到总的等效电感\(L\)：

\[V=L_1\frac{dI}{dt}+L_2\frac{dI}{dt}+L_3\frac{dI}{dt}=(L_1+L_2+L_3)\frac{dI}{dt} \]

其中，\((L_1+L_2+L_3)\)称为这3个串联电感的等效电感.

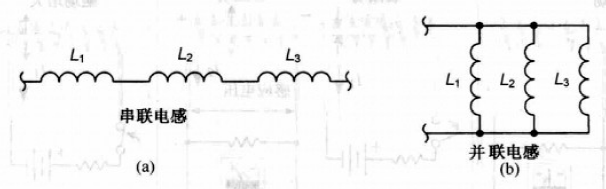
• 并联电感

\[L_{tot}=\frac{1}{L_1}+\frac{1}{L_2}+...+\frac{1}{L_N} \]

并联电感计算公式，也可以用基尔霍夫电流定律求出. 如上图，对电路\(L_1\)上部节点求电流

\[\begin{aligned} I&=I_1+I_2+I_3\\ &=\frac{1}{L_1}\int Vdt+\frac{1}{L_2}\int Vdt+\frac{1}{L_3}\int Vdt\\ &=(\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3})\int Vdt \end{aligned} \]

注：\(V=LdI/dt\to I=\frac{1}{L}\int Vdt\)

其中，\((\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3})\)是等效电感.

感抗

电感的交变电流幅值 与 电源频率 成反比.
给定电流变化率时，反向电压 ∝ 电感. 在给定电源电压和频率下，电流 与 电感成反比. 把电感与频率的合成效应，称为感抗，单位：Ω.

感抗计算：

\[X_K=2πfL=ωfL \]

其中，π=3.1416，f频率，L电感，ω角频率

感抗表达式可用将电感连接至正弦电压源上得出. 为计算方便，用余弦函数替换正弦函数（实际上没有区别），e.g. 电源电压\(V_0cos (ωt)\)，则电感元件上电流：

\[I=\frac{1}{L}\int Vdt=\frac{1}{L}\int V_0cos(ωt)dt=\frac{V_0}{ωL}sin(ωt) \]

注：\(sin'(ωt)=ωcos(ωt)\)

\(sin(ωt)=1\)时，电感电流达到最大值：

\[I_0=\frac{V_0}{ωL} \]

峰值电压、电流的比值类似电阻，有欧姆量纲，但不同于电阻，因为不发热，所以有个感抗这个新名称.

\[X_L=\frac{V_0}{I_0}=ωL \]

实际电感模型

考虑电感内阻和电容.

一个实际电感可用4个无源理想元件来模拟：串联电感（L），串联电阻（\(R_{DC}\)），并联电容\(C_p\)，并联电阻\(R_p\)

制造商通常会在datasheet上注明直流电阻值.

下图左是实际电感模型，中是等效电感电路，右是分布电容与电感发生谐振时的曲线：

参考

[1] 美 舍茨 Scherz, Paul.实用电子元器件与电路基础[M].电子工业出版社,2009.