电路基础：电容器

目录

• 电容器
  • 工作原理
  • 电容的确定
  • 商用电容器
  • 额定电压、介质击穿
  • 电容器的电流模型
  • 电容器的能量
  • 时间常数
  • 寄生电容
  • 电容并联
  • 电容串联
  • 容抗
  • 电容性分压器
• 参考

电容器

工作原理

什么是电容器？

在两块带有相反极性电荷的平行导板间置入绝缘介质，如空气、陶瓷，即可制成电容器.

如果用电池给电容器两端施加电压，那么电子会从 电池负极端 流出，积聚在下极板上，同时，有电子从 上极板 流出，积聚到 电池正极上.

一句话：上极板将缺乏电子，下极板将汇聚电子.

电容器工作原理示意图：

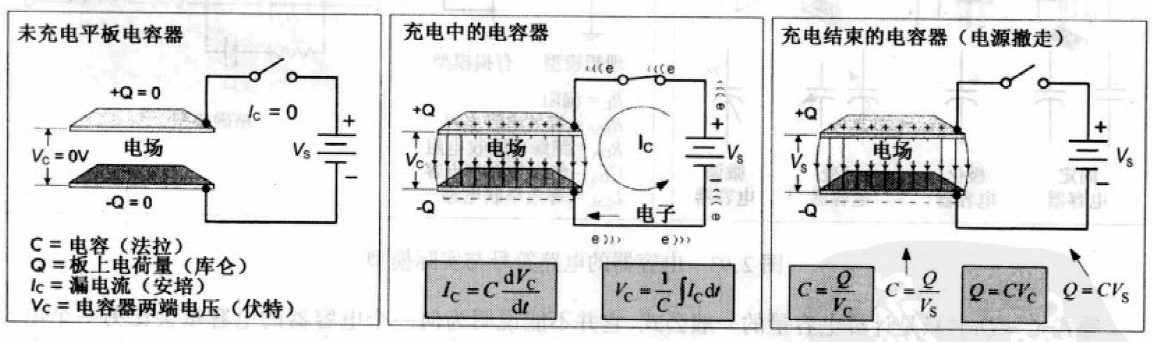
充电：接上电池时，上极板出现正电荷+Q，下极板出现负电荷-Q，电荷在电极板直接产生电场，板间电压 = 电池电压. 当电容器与电池没有电压差时，电子停止流动，系统达到平衡，此时，充电结束.

若此时移去电容器两端电池，而不短接电容，那么极板上的电荷、板间电场、电压维持不变.

当然，实际情况是，充电的电容器脱离电源后，最终会失去电荷. 因为极板间空气/介质的绝缘特性不是理想的，移除电源后，会出现“漏电流”，电容器会在几秒~几小时后完全放电.

放电：如果想给电容器快速放电，可用一根导线将2个极板连接，形成从-极板到+极板的导电通路，系统变为中性.

电容器极板上电荷量Q与板间电压V的比值，称为电容C：

\[C=\frac{Q}{V} \]

C总取正值，单位法拉，F.

\[1 F = 1 C/1 V \]

电容器是用来保存电荷或以电场形式存储电能的器件.

电容器符号与实际模型：

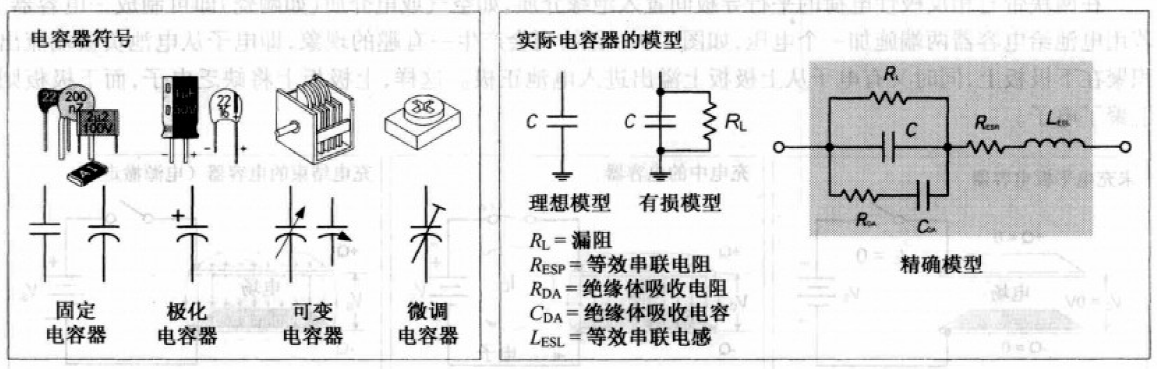
电容的确定

电容器的电容C与极板面积A、极板间距离d、绝缘材料或电介质有关. 如果给2平行极板施加电压V，则极板间的电场强度\(E=V/d\)

根据电荷守恒，2极板上必带有等量、异号的电荷.

根据高斯定理，

\[\oint_S \bm{E}d\bm{A}=\frac{Q _{enc}}{ε_0} \]

其中，

• 电场强度\(\bm{E}\)（矢量）
• 闭合曲面S
• \(d\bm{A}\)，S上的微面积矢量
• \(Q _{enc}\)，S内包围的净电荷（单位：库仑，C）
• \(ε\)，介电常数

净电荷，指一个系统内，所有+电荷、-电荷的代数和.

将其应用到电容两极板：

\[Q=εEA=\frac{εAV}{d} \]

自由空间或真空的介电常数：\(ε_0=8.85×10^{−12} F/m\)

一种介质的介电常数与真空中的介电常数的比值，称为相对介电常数：

\[k=\frac{ε}{ε_0} \]

∴电容的一种计算公式

\[C=\frac{Q}{V}=\frac{εA}{d}=\frac{kε_0A}{d} \]

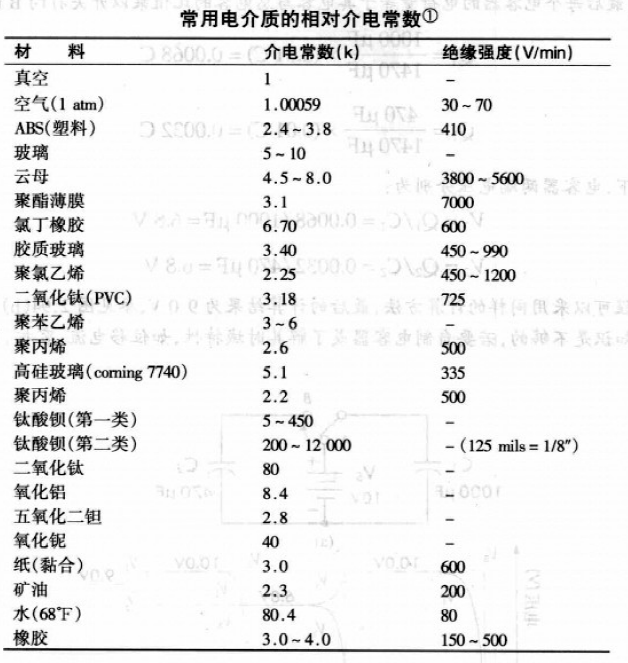
商用电容器

商用电容器：极板为金属薄片制成，板间填充薄层固态或液态介质.
常用固态介质：云母、纸、聚丙烯、特殊陶瓷

特点：体积小、电容量大

电解电容器：极板用铝箔制成，板间填充半液体状的导电化合物.
通过给电容器加直流电压产生化学反应，使电介质在其中一组极板上形成非常薄的绝缘薄膜.

特点：一定面积的电解电容器的电容，要比其他介质电容器的电容大，因为其电介质薄膜比任何固态电介质的要薄.

额定电压、介质击穿

电容器内介质起绝缘作用. 绝缘体内部电子不能脱离原子，但如果施加足够高电压，电介质内的电子就会脱离原子，导致电介质击穿.

电介质击穿电压与化学成分、厚度有关. 其他因素：电极形状、间隙长度、气压或气体密度、电压、电介质的纯度电路外部环境（如湿度、温度 etc.）.

电容器的电流模型

对于理想电容器，电容表达式微分形式：

\[C=\frac{dQ}{dV}\iff dQ=CdV \]

其中，电容C是不随电荷、电压、时间改变的常量

由电流定义，流过电容的电流：

\[I_C=\frac{dQ}{dt}=C\frac{dV_C}{dt} \]

其中，\(dV_C\)电容两端电压微分

反过来，可求出\(V_C\)

\[V_C=\frac{1}{C}\int I_Cdt \]

如下图，dt时间内，有微量电荷dQ流入右极板，同时左极板出现相同电荷dQ.

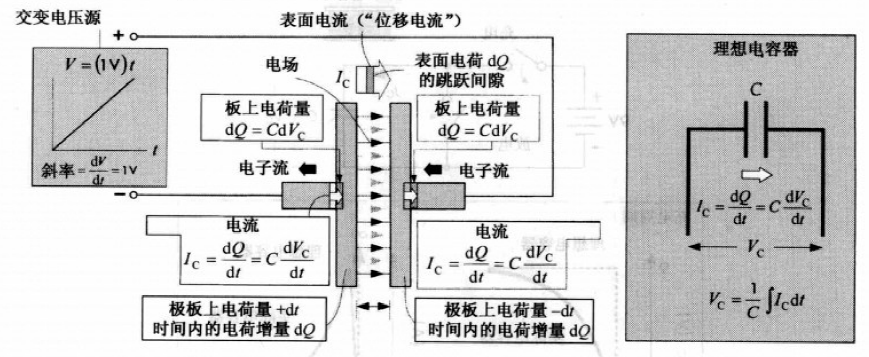
电容器的能量

能量在理想电容器中不会被消耗，但对含有内阻的实际电容不成立. 因为实际电容内阻很小，所以经常忽略其消耗的能量.

电容器的功率：\(P=IV\)

又由功率定义，

\[P=\frac{dE}{dt} \]

其中，dE是微分时间dt电容器的能量变化

对E积分，

\[\begin{aligned} E_{cap} &=\int Pdt=\int VIdt\\ &=\int VdQ=\int VCdV\\ &=\frac{1}{2}CV^2 \end{aligned} \]

例：给1个1000μF电容器施加5V电压，求电容器的能量

解：

\[E_{cap}=\frac{1}{2}CV^2=\frac{1}{2}\cdot (1000\cdot 10^{-6}F)\cdot (5V)^2=0.0125J \]

时间常数

电容器接直流电压源两端，几乎瞬间完成充电. 因为含内阻，所以用几乎.

如果用导线连接两端，几乎瞬间完成放电.

如果电路中接入电阻，充电、放电、的速率将遵循一指数规律.

常用应用场景：定时集成电路、振荡电路、波形发生电路、低放电功率存储电路

RC充电电路电流、电压：

\[\begin{aligned} I&=\frac{V_S}{R}e^{-\frac{t}{RC}} \iff \frac{t}{RC}=-ln(\frac{IR}{V_S})\\ V_R&=IR=V_Se^{-\frac{t}{RC}}\iff \frac{t}{RC}=-ln(\frac{V_R}{V_S})\\ V_C&=\frac{1}{C}\int Idt=V_S(1-e^{-\frac{t}{RC}})\iff \frac{t}{RC}=-ln(\frac{V_S-V_C}{V_S}) \end{aligned} \]

其中，时间常数\(τ=RC\)(单位：秒)，t为接入电压源后的时间（单位：秒）,e=2.718，\(V_R、V_C\)分别为电阻电压、电容电压

理论上，充电时间将趋于无穷，但充电电流最终将减小至不可测的数值.

通常令\(τ=RC\)为电路时间常数（单位：秒），经过1τ后（t=τ），电容的充电电压达到电源电压的63.2%；经过2τ后(t=2τ)，电容电压达电源电压86.5%；3τ后，电容电压为电源电压的95%.

寄生电容

电容不仅存在于电容器内部，2个不同电位的表面互相靠近时，就会产生电场，存在电容效应，作用如同电容器.

这种无意间形成的电容，并非人为的，称为寄生电容.

寄生电容对高阻抗电路、敏感电路影响较大：

1）高阻抗电路，容性电抗占电路阻抗的比例较大

2）敏感电路中，寄生电容通常与电路并联，频率较高时，将起到旁路信号作用.

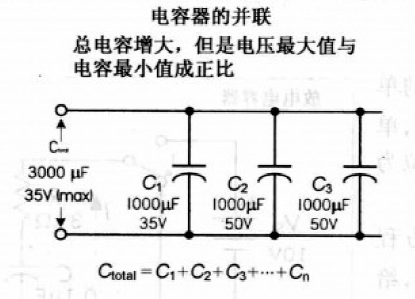
电容并联

电容并联时，总电容为各电容相加，计算类似于电阻串联：

\[C_{tot}=C_1+C_2+...+C_n \]

如下图，3个电容并联，对电路上部节点应用基尔霍夫电流定理，可得出等效电容：

\[I=C_1\frac{dV}{dt}+C_2\frac{dV}{dt}+C_3\frac{dV}{dt}=(C_1+C_2+C_3)\frac{dV}{dt} \]

电容串联

电容串联，总电容小于最小电容器的容值，计算类似于电阻并联：

\[\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+...+\frac{1}{C_n} \]

对环路应用基尔霍夫电压定理，

\[\begin{aligned} V&=\frac{1}{C_1}\int Idt+\frac{1}{C_2}\int Idt+...+\frac{1}{C_n}\int Idt\\ &=(\frac{1}{C_1}+\frac{1}{C_2}+...+\frac{1}{C_n})\int Idt \end{aligned} \]

括号内是等效电容.

容抗

电容器上的电荷\(Q=CV\). 在一个交流电路中，电荷在电路中做周期性的往返运动，电荷（或电流）的运动速度与电压、电容、频率成正比. 将电容、频率相乘，得到一个类似于电阻的量，由于没有热量产生，因此将这一量称为容抗，单位：Ω.

容抗计算：

\[X_C=\frac{1}{2πfC}=\frac{1}{ωC} \]

其中，\(X_C\)容抗（单位：Ω），频率f（单位：Hz），电容C（单位：F），π=3.1416，角频率ω=2πf

用位移电流公式，也能推导出容抗公式：

\[I=\frac{dQ}{dt}=C\frac{dv}{dt}=-ωCV_0sin(ωt) \]

\(sin(ωt)=-1\)时，电流达到最大值/峰值\(I_0=ωCV_0\)

比值\(V_0/I_0=1/(ωC)\)类似于欧姆定律中电阻，单位：Ω. 但“阻抗”线性不同于传统电阻器，因此将该阻抗称为容抗.

\(f\to ∞\)时，\(X_C=0\)，即高频时认为电容器短路；
\(f=0\)时，\(X_C\to ∞\)，即任务电容器断路.

注意：容抗不消耗电能. 在1/4周期内存储在电容器中电脑，到下一个1/4周期又会直接释放回电路.

例：给220pF电容器两端加10MHz电压源，求出电容器的容抗.

解：

\[\begin{aligned} X_C&=\frac{1}{2πfC}\\ &=\frac{1}{2π\cdot 10\cdot 10^6\cdot 220\cdot 10^{-12}}Ω\\ &=72.343Ω \end{aligned} \]

电容性分压器

电容性分压器用于输入交流信号的电路中，因为电容器隔断直流，所以直流电路不能用电容性分压器.

电容性分压器的交流输出电压计算公式，不同于电阻分压器的计算. 如下图，分压公式的分子是串联元件\(C_1\)，而非\(C_2\)

注：输出电压\(V_{out}\)与输入频率f无关

如果是电阻分压器，

\[V_{out}=\frac{R_1}{R_1+R_2}V_{in} \]

参考

[1] 美 舍茨 Scherz, Paul.实用电子元器件与电路基础[M].电子工业出版社,2009.

[2] https://baike.baidu.com/item/高斯定理

[3] 电路基础：交流电路