电机控制笔记：PMSM无位置传感器控制介绍

目录

• 概述
  • 介绍
  • 永磁电机
  • 拓扑结构
  • 驱动系统
  • 永磁无刷交流电机驱动基本原理
    • 数学模型
      • ABC三相坐标系
      • 静止坐标系
      • 同步旋转坐标系
    • 控制策略
      • 空间矢量脉宽调制
      • 磁场定向控制 FOC
      • 直接转矩控制 DTC
      • 模型预测控制
  • 永磁无刷直流电机驱动的基本原理
    • 数学模型
    • 控制策略
  • 永磁无刷直流电机 vs 永磁无刷交流电机驱动
    • 方波反电动势电机
    • 正弦波反电动势电机
  • 无位置传感器控制技术及其应用
    • 分类
    • 应用
• 参考

概述

介绍

永磁同步电机（Permanent Magnet Synchronous Machine，PMSM），包括永磁无刷交流电机（Brushless AC Machine，BLACM）、永磁无刷直流电机（Brushless DC Machine，BLDCM）.

通常，PMSM仅指永磁BLAC电机；本文同时使用永磁BLACM、PMSM，“永磁电机”特指“永磁无刷电机”.

永磁电机

优点：高效率、高转矩密度、高功率密度、易维护等.

拓扑结构

永磁同步电机分类：

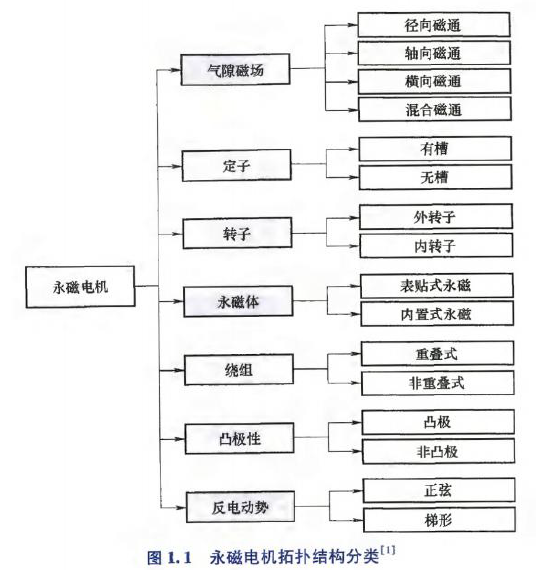
• 从气隙磁场类型看

永磁电机可分为：径向磁通永磁电机、轴向磁通永磁电机、横向磁通永磁电机、混合磁通永磁电机.

与径向磁通永磁电机相比，轴向磁通、横向磁通的 具有更高的转矩密度和功率密度，不过制造工艺更复杂.

• 从定子绕组结构看

永磁电机可分为：
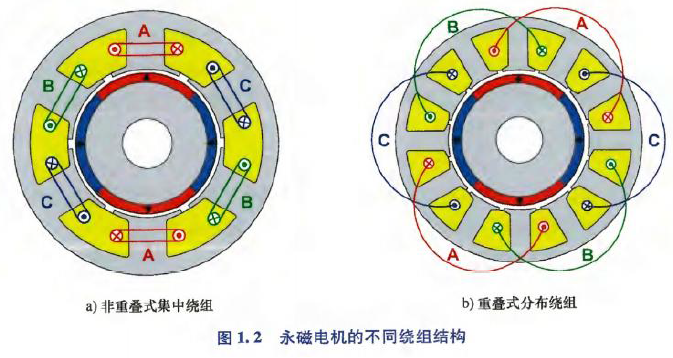
1）非重叠式集中绕组的分数槽电机；
2）重叠式分布绕组的整数曹电机.

集中式绕组的端部绕组更短、槽满率更高，减少了电机总体积、总质量、铜损 => 整体效率、转矩密度更高.

分数槽永磁电机的定子磁动势（Magneto-Motive Force，MMF）谐波含量较高，可能导致永磁体的涡流损耗增加、局部磁饱和、噪声、振动等问题.

• 从转子结构看

永磁电机的转子结构可分为：
1）表贴式永磁（Surface-Mounted PM，SPM）电机；
2）内置式永磁（Interior PM、IPM）电机.

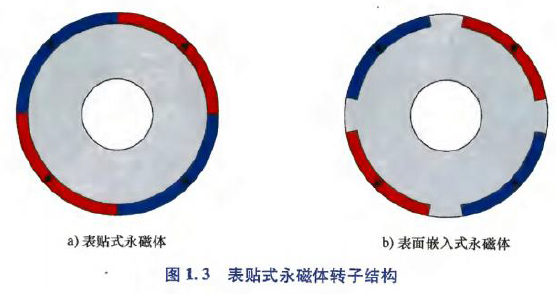
SPM电机（SPMSM）结构简单、制造成本低，永磁体形状易优化，在气隙中能产生更接近正弦分布的磁通密度；但由于直接暴露在电枢磁场中，永磁体存在不可逆退磁风险. 通常，SPM永磁体应由不锈钢护套或玻璃/碳纤维固定.

表面嵌入式永磁电机(特殊的SPMSM)，永磁体嵌入转子铁芯中，相邻永磁体由铁芯隔开. 由于在永磁体之间采用了高磁导率的铁芯材料，转子有一定凸极性，因此，可用磁阻转矩来提高转矩密度和/或减少永磁体用量.

表贴式永磁体转子结构：

tips：
凸极性（Saliency）指电机转子的结构或磁场分布导致直轴（d-axis）和交轴（q-axis）磁路磁阻（或电感）不相同的特性，这种差异会影响电机的电磁性能和控制策略.

将永磁体置于转子铁芯内部的IPM结构，转子凸极性显著、弱磁能力强、永磁体退磁风险低.

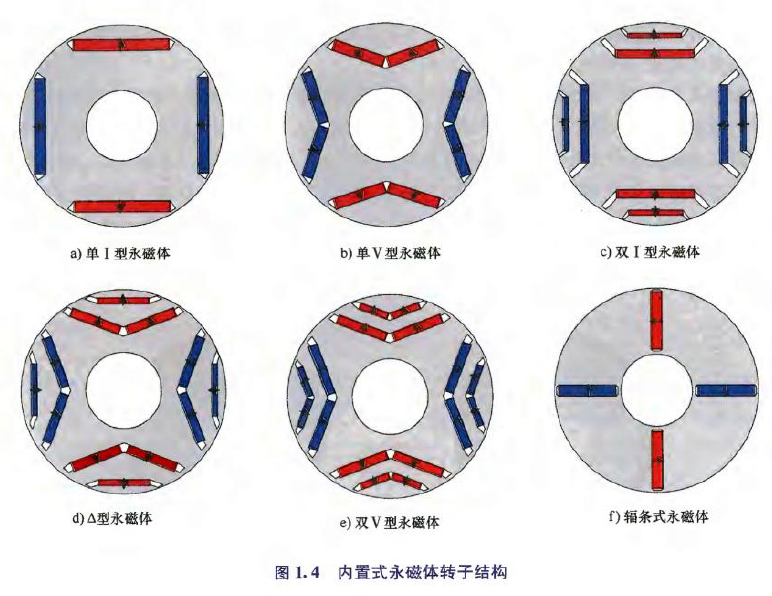
根据转子永磁体结构，IPM电机（IPMSM）可分为：单层IPM转子，下图Ⅰ型、Ⅴ型；双层IPM转子，下图双Ⅰ型、Δ型、双Ⅴ型；辐条式转子等.

1）Ⅰ型IPM转子结构简单，有凸极性；
2）单层Ⅴ型IPM转子增大了永磁体横截面积，增强了聚磁效果，从而提高输出转矩；
3）双层IPM转子（双Ⅰ型、Δ型、双Ⅴ型），转子凸极性、磁阻转矩得到进一步提高，但制造工艺更复杂；
4）辐条型IPM转子，如果采用较高级数，聚磁效应会很显著，但由于轴附近存在额外磁桥，因此漏磁通较高，应采用非磁性轴，且轴附近的叠片需要气隙磁通屏障.

驱动系统

永磁无刷电机驱动系统通常由控制器、逆变器、永磁电机组成. 电流可通过三相电流、两相电流、直流母线电流进行测量，转子速度、位置的测量需要借助位置传感器，或者无位置传感器技术，电压传感器测量直流母线电压. 反馈信号被送到控制器，由控制器生成逆变器所需开关信号，以实现控制目标.

如下图，典型的PMSM驱动系统框图：

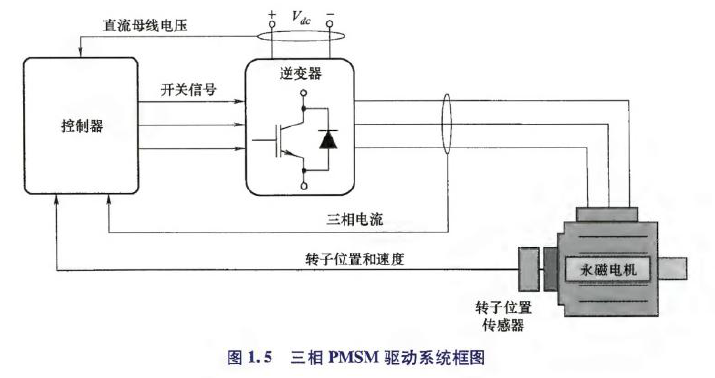
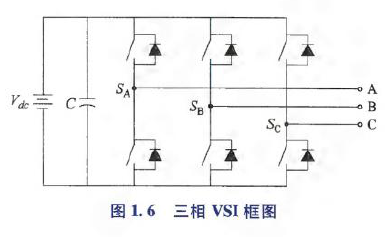
下图是三相电压源型逆变器（Voltage Source Inverter，VSI），常用于三相永磁无刷驱动系统. VSI由6个功率半导体开关（IGBT绝缘栅双极型晶体管，或MOSFET金属氧化物半导体场效应晶体管）组成，这6个开关组成一个三相桥，每一相桥臂由上下2个开关组成；每相桥臂中点连接到永磁电机定子绕组端；三相桥臂与直流电压源相连，同时直流母线电容用于平滑直流母线电压.

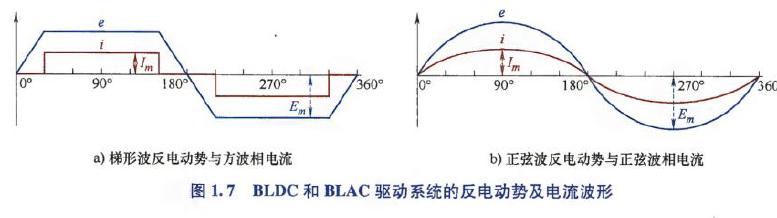
转子旋转时，定子绕组中会产生反电动势（back Electromotive Force，back-EMF）. 永磁电机可根据反电动势波形分为正弦波、梯形波（理想情况 方波）.

根据逆变器开关状态选择方式，控制测量可分为：BLDC、BLAC运行模式. 在BLDC模式运行，逆变器应产生方波电流；在BLAC模式运行，逆变器产生正弦波电流. BLAC驱动系统使用SVPWM控制三相导通，来产生正弦波电流；BLDC驱动系统则采样六步法控制的两相导通来产生方波电流.

永磁无刷交流电机驱动基本原理

下面介绍BLAC驱动系统的数学模型、控制策略.

数学模型

三相PMSM可在不同坐标系中建立数学模型，包括ABC三相坐标系、静止坐标系、同步旋转坐标系.
为简化模型，需要以下假设：

• 定子绕组在空间上对称分布，从而产生正弦电枢反应磁动势
• 转子上的永磁体在定子绕组中感应产生的电动势为正弦
• 三相绕组为星形联结，无中性点引出
• 忽略电机铁芯的损耗、饱和效应
• 忽略温度、负载引起的参数变化

电枢：电机核心部件，负责能量转换. 在BLCD或PMSM中，通常指定子绕组.

磁动势：驱动磁场在磁路中产生的“推动力”，类似于电路中的电动势（EMF），单位：安培（A）或安匝（At）（如果考虑线圈匝数）.

磁动势物理意义：MMF是磁路中磁场强度来源，决定磁通量大小.
电动势（EMF）驱动电流在电路中流动；磁动势（MMF）驱动磁通（φ）在磁路中形成磁场.

磁动势计算：

\[\mathcal{F} = N \cdot I [At] \]

其中，\(\mathcal{F}\)磁动势，N线圈匝数，I通过线圈的电流

磁路欧姆定律：

\[φ=\frac{\mathcal{F}}{\mathcal{R}} \]

其中，\(φ\)磁通量；\(\mathcal{R}\)磁阻，取决于磁路的材料（如铁芯、空气隙）、几何尺寸.

ABC三相坐标系

三相坐标系中，PMSM电压方程：

\[\begin{bmatrix} v_a\\v_b\\v_c \end{bmatrix} =\begin{bmatrix} R_s & 0 & 0\\0 & R_s & 0\\0 & 0 & R_s \end{bmatrix} \cdot \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} +p\begin{bmatrix} ψ_a\\ψ_b\\ψ_c \end{bmatrix} \]

其中，\(v_a,v_b,v_c\)三相电压；\(i_a,i_b,i_c\)三相电流；\(ψ_a,ψ_b,ψ_c\)三相定子磁链；\(R_s\)相电阻；p微分算子，即\(p=d/dt\)

三相定子磁链：

\[\begin{bmatrix} ψ_a\\ψ_b\\ψ_c \end{bmatrix} =\begin{bmatrix} L_{AA} & M_{AB} & M_{AC}\\ M_{BA} & L_{BB} & M_{BC}\\ M_{CA} & M_{CB} & L_{CC} \end{bmatrix} \cdot \begin{bmatrix} i_a\\i_b\\i_c \end{bmatrix} +ψ_m\begin{bmatrix} cos θ_r\\cos(θ_r-2π/3)\\cos(θ_r+2π/3) \end{bmatrix} \]

其中，\(L_{AA},L_{BB},L_{CC}\)三相绕组的自感；\(M_{AB},M_{BA},M_{AC},M_{CA},M_{BC},M_{CB}\)三相绕组的互感；\(ψ_m\)永磁磁链；\(θ_r\)电角度.

磁链是指穿过线圈的总磁通量与其匝数的乘积. 磁链\(Ψ=N\cdot Φ\)，其中，N线圈匝数，\(Φ\)穿过单匝线圈的磁通量

磁通量定义：
\(Φ=\int_S \bm{B}\cdot d\bm{A}\)
其中，\(\bm{B}\)磁感应强度，\(d\bm{A}\)曲面S上的面元

电感矩阵：

\[\begin{cases} L_{AA}=L_{s0}-L_{s2}cos 2θ_r\\ L_{BB}=L_{s0}-L_{s2}cos 2(θ_r-2π/3)\\ L_{CC}=L_{s0}-L_{s2}cos 2(θ_r+2π/3) \end{cases} \]

其中，\(L_{s0},L_{s2}\)分别为自感的直流分量、2次谐波分量的幅值.

\[\begin{cases} M_{AB}=M_{BA}=M_{s0}-M_{s2}cos 2(θ_r+2π/3)\\ M_{BC}=M_{CB}=M_{s0}-M_{s2}cos 2θ_r\\ M_{CA}=M_{AC}=M_{s0}-M_{s2}cos 2(θ_r-2π/3) \end{cases} \]

其中，\(M_{s0},M_{s2}\)分别为互感的直流分量、2次谐波分量的幅值，且非凸极电机没2次谐波分量，即\(L_{i2}=M_{i2}=0\)

从上面式子可看出，ABC三相坐标系下，电机的数学模型与转子位置耦合，这会极大增加控制复杂度. 因此，将电机数学模型转换为静止坐标系和同步坐标系更好.

自感与互感区别：

当一个线圈中的电流变化时，它会在自身产生感应电动势（EMF），这种现象称为自感.

\[\mathcal E_{self}=-L\frac{di}{dt} \]

其中，\(L\)自感系数，\(\frac{di}{dt}\)电流变化率.

当一个线圈（初级）的电流变化时，会在另一个线圈（次级）中感应出电动势，这种现象称为互感.

\[\mathcal E_{mutual}=-M\frac{di_1}{dt} \]

其中，M互感系数，\(\frac{di_1}{dt}\)初级线圈电流变化率.

静止坐标系

通过Clarke变换，可将电机的数学模型从ABC三相坐标系变化到αβ静止坐标系：

\[T_{ABC-αβ} = \frac{2}{3}\begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt 3}{2} & -\frac{\sqrt 3}{2}\\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix}, T_{αβ-ABC} = \begin{bmatrix} 1 & 0 & 1\\ -\frac{1}{2} & \frac{\sqrt 3}{2} & 1\\ -\frac{1}{2} & -\frac{\sqrt 3}{2} & 1\ \end{bmatrix} \]

ABC坐标系与αβ坐标系关系：

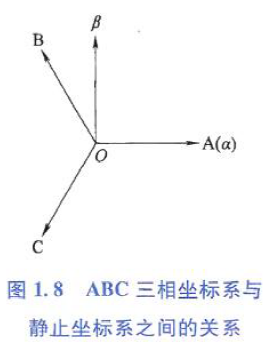
假设三相绕组为星形联结，无中性点引出，则三相电流和为零（基尔霍夫电流定律），即零序分量为零. 变换后，αβ坐标系下电压方程、磁链方程分别为：

\[\begin{aligned} \begin{bmatrix} v_α\\v_β \end{bmatrix} &=\begin{bmatrix} R_s & 0\\0 & R_s \end{bmatrix} \cdot \begin{bmatrix} i_α\\i_β \end{bmatrix} +p\begin{bmatrix} ψ_α\\ψ_β \end{bmatrix}\\ \begin{bmatrix} ψ_α\\ψ_β \end{bmatrix} &=\begin{bmatrix} L_{αα} & M_{αβ}\\ M_{βα} & L_{ββ}\\ \end{bmatrix} \cdot \begin{bmatrix} i_α\\i_β \end{bmatrix} +ψ_m\begin{bmatrix} cos θ_r\\sin θ_r \end{bmatrix} \end{aligned} \]

其中，\(v_α,v_β,i_α,i_β,ψ_α,ψ_β\)静止参考坐标系中的αβ轴电压、电流、磁链，\(L_{αα},L_{ββ},M_{αβ},M_{βα}\)是自感、互感.

\(αβ\)轴电感：

\[\begin{cases} L_{αα}=\frac{L_d+L_q}{2}+\frac{L_d-L_q}{2}cos 2θ_r\\ L_{ββ}=\frac{L_d+L_q}{2}-\frac{L_d-L_q}{2}cos 2θ_r\\ M_{αβ}=M_{βα}=\frac{L_d-L_q}{2}cos 2θ_r \end{cases} \]

其中，\(L_d,L_q\)分别d轴、q轴电感

如果电机是非凸极，即SPM，则电感关系：\(L_d=L_q=L_s\)

同步旋转坐标系

电机模型可通过Park变换从静止坐标系（αβ）转换到同步旋转坐标系（dq），变换：

\[T_{αβ-dq}=\begin{bmatrix} cos θ_r & sin θ_r & 0\\ -sin θ_r & cos θ_r & 0\\ 0 & 0 & 1 \end{bmatrix}, T_{dq-αβ}=\begin{bmatrix} cos θ_r & -sin θ_r & 0\\ sin θ_r & cos θ_r & 0\\ 0 & 0 & 1 \end{bmatrix} \]

也可用DQZ变换将电机模型从ABC坐标系变换到同步旋转坐标系，DQZ变换是Clarke变换、Park变换的乘积：

\[\begin{aligned} T_{ABC-dq} &= T_{ABC-αβ}\cdot T_{αβ-dq}=\frac{2}{3}\begin{bmatrix} cos θ_r & cos (θ_r-2π/3) & cos (θ_r+2π/3)\\ -sin θ_r & -sin (θ_r-2π/3) & -sin (θ_r+2π/3)\\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix}\\ T_{dq-ABC} &= T_{dq-αβ}\cdot T_{αβ-ABC}=\begin{bmatrix} cos θ_r & -sin θ_r & 1\\ cos(θ_r-2π/3) & -sin(θ_r-2π/3) & 1\\ cos(θ_r+2π/3) & -sin(θ_r+2π/3) & 1 \end{bmatrix} \end{aligned} \]

ABC三相坐标系、静止坐标系（αβ）、同步旋转坐标系（dq）关系如图：

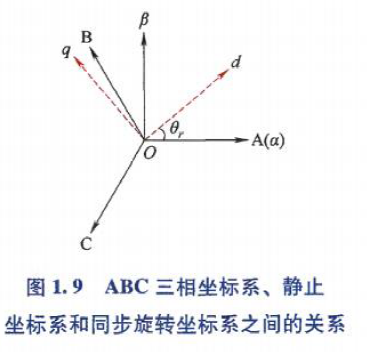
忽略零序分量，同步旋转坐标系中电压方程、磁链方程分别为：

\[\begin{aligned} \begin{bmatrix} v_d\\v_q \end{bmatrix} &=\begin{bmatrix} R_s & 0\\0 & R_s \end{bmatrix} \cdot \begin{bmatrix} i_d\\i_q \end{bmatrix} +p\begin{bmatrix} ψ_d\\ψ_q \end{bmatrix}+ω\begin{bmatrix} -ψ_q\\ψ_d \end{bmatrix}\\ \begin{bmatrix} ψ_d\\ψ_q \end{bmatrix} &=\begin{bmatrix} L_{d} & 0\\ 0 & L_{q}\\ \end{bmatrix} \cdot \begin{bmatrix} i_d\\i_q \end{bmatrix} +ψ_m\begin{bmatrix} 1\\0 \end{bmatrix} \end{aligned} \]

其中，\(v_d,v_q,i_d,i_q,ψ_d,ψ_q\)分别为同步旋转坐标系下的dq轴电压、电流、磁链；\(ω_r\)为电角速度.

控制策略

理想永磁BLAC电机的三相反电动势为正弦，基于此，将三相电流控制为正弦波，并与反电动势同相位或超期反电动势，从而获得最大输出转矩.
为实现三相正弦波电流，通常采用SVPWM来控制VSI产生电机所需的定子电压. 定子电压的参考值可通过控制策略获取：磁场定向控制（Field-Oriented Control，FOC）、直接转矩控制（Direct Torque Control， DTC）、模型预测控制（Model Predictive Control，MPC）.

空间矢量脉宽调制

SVPWM常用于BLAC驱动系统，控制VSI输出电压，从而实现电机的速度、转矩控制.

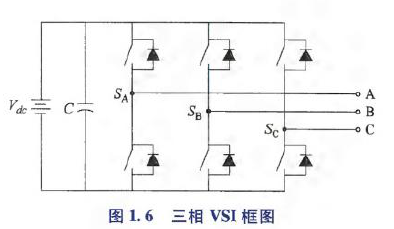
\(S_A,S_B,S_C\)表示VSI三个桥臂的开关状态. 为避免短路，每条桥臂中的上下开关为互补模式，且在实际应用中需要加入死区时间.

VSI共8个开关状态：

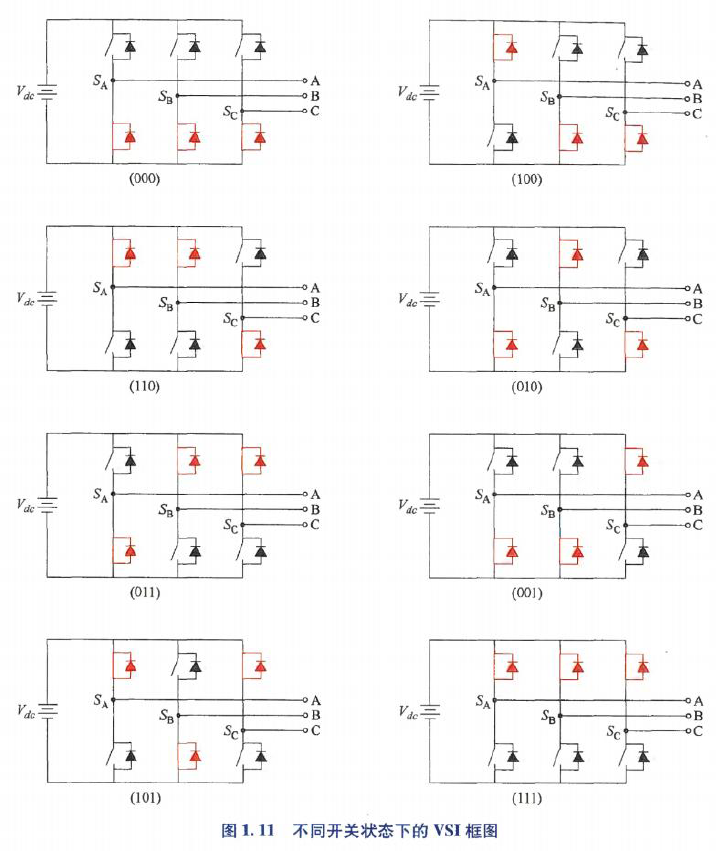
不同开关状态的等效电路：

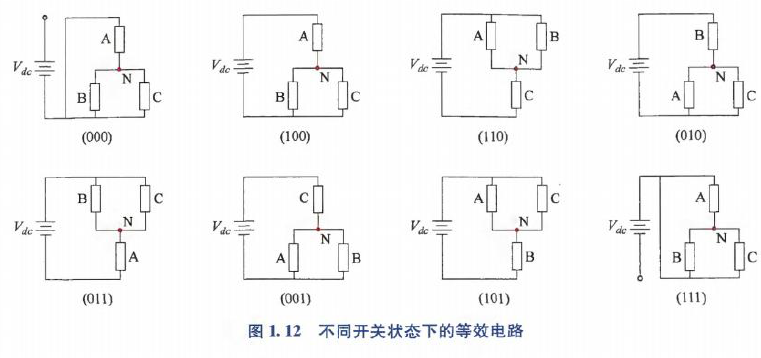
根据等效电路，可知不同开关状态下的相电压：

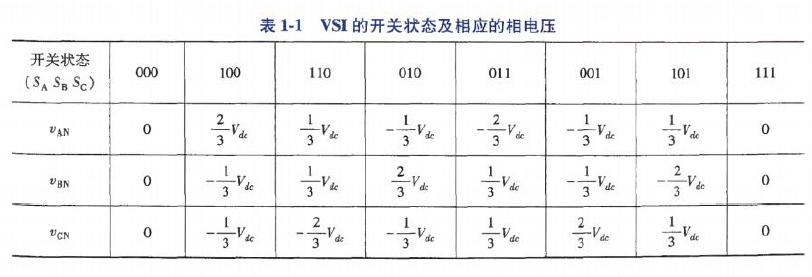
基于旋转空间矢量的概念，VSI的三相电压可构成一个等效的电压矢量（即合成矢量）：

\[v_s=v_{AN}+v_{BN}e^{j\frac{2}{3}π}+v_{CN}e^{j\frac{4}{3}π} \]

其中，\(v_{AN},v_{BN},v_{CN}\)为相电压

如果以A相为基准，

\[\begin{cases} v_{AN}=v_mcos ωt\\ v_{BN}=v_mcos (ωt+120°)\\ v_{CN}=v_mcos (ωt-120°) \end{cases} \]

其中，\(v_m\)是相电压幅值，\(ω=2πf\)角速度，三相相位差120°.

在静止坐标系中，\(v_s\)可写成：

\[v_s=v_{AN}+v_{BN}e^{j\frac{2}{3}π}+v_{CN}e^{j\frac{4}{3}π}=v_α+jv_β \]

参见：电机控制笔记：理解直流无刷电机矢量控制 合成矢量的推导

VSI开关状态中，共有8个基本电压矢量，其中6个非零矢量\(v_1,...,v_6\)，2个零矢量\(v_{0,7}\)

不同开关状态下的8个基本电压矢量：

在静止坐标系中，非零电压矢量形成一个幅值为\(2V_{dc}/3\)的六边形，整个区域被电压矢量划分为六个扇形.

利用八个基本电压矢量，VSI可在一个采样周期内，通过合成两个相邻的非零矢量、一个零矢量来生成一个任意的旋转电压矢量. 如下图，扇区Ⅰ的参考电压矢量\(v_s\)，可由2个非零矢量\(v_1,v_2\)、零矢量\(v_0\)来合成.

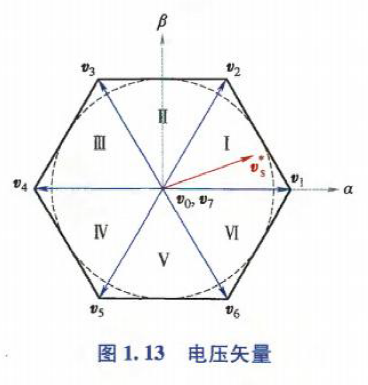
根据作用时间，电压矢量的合成可表示为：

\[v_s^* T_s = v_1T_1 + v_2T_2 + v_0T_0\\ T_s=T_1+T_2+T_0 \]

其中，\(T_1,T_2,T_0\)分别为电压矢量\(v_1,v_2,v_0\)的作用时间

举例说明合成过程：

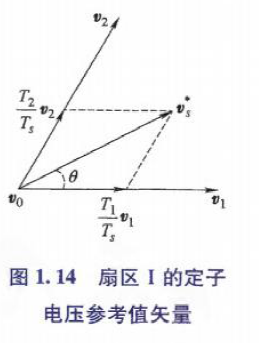
如上图，由正弦定理，\(△ov_1v_s^*\)中，

\[\frac{v_s^*}{sin \frac{2π}{3}}=\frac{\frac{T_1}{T_s}v_1}{sin (\frac{π}{3}-θ)}=\frac{\frac{T_2}{T_s}v_2}{sin θ} \]

注意：
\(v_1,v_2\)夹角为\(π/3\).

可得，

\[\begin{cases} T_1=\frac{\sqrt 3V_s^*}{V_{dc}}T_ssin(\frac{π}{3}-θ)\\ T_2=\frac{\sqrt 3V_s^*}{V_{dc}}T_ssin(θ)\\ T_0=T_s-T_1-T_2 \end{cases} \]

其中，\(V_s^*\)定子电压参考值的幅值，\(θ\)定子电压参考值的角度.

注：查表可得\(v_0,...,7\)与\(v_{dc}\)关系

对其他扇区，类似方法可推导出电压矢量的作业时间.

推导过程可参见电机控制笔记：理解直流无刷电机矢量控制 矢量作用时间分析

获得电压矢量的持续时间后，下一步需要确定开关顺序（开关状态顺序）. 下图是在扇区Ⅰ内，所用开关序列的一个示例：

为减少开关损耗，从一个开关状态到下一个的转换仅通过1个开关动作来完成（不是2个）. 因此，在一个开关周期的中间应用零矢量\(v_7\)，而非零矢量\(v_0\)

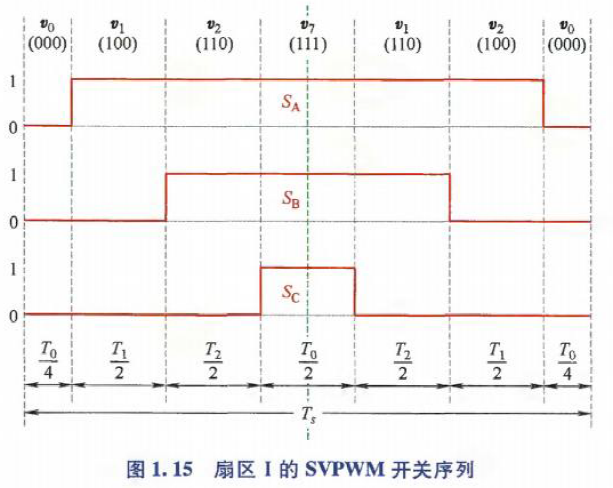
零矢量的分配是为了产生对称PWM，可有效降低输出电压的谐波分量.

当参考电压矢量位于六边形的内切圆内时，SVPWM算法生成的旋转电压矢量的轨迹可以是六边形内的一个圆，确保了输出三相电压的基波分量是幅值、频率恒定的正弦波；
如果参考电压矢量位于六边形内切圆外，则需要使用过调制方案来产生所需输出电压.

磁场定向控制 FOC

FOC或称矢量控制（Vector Control，VC），可将三相交流（AC）电机作为直流（DC）电机进行控制.

基于坐标变换，三相正弦电流被转化为2个正交的直流分量：1个控制磁链，另1个控制转矩. 通过使用FOC，PMSM（BLAC）驱动系统能拥有出色的控制性能，可以实现全转速范围运行，即使在零转速时，也能保证理想的转矩控制. 此外，FOC还有良好的动态性能、精度控制.

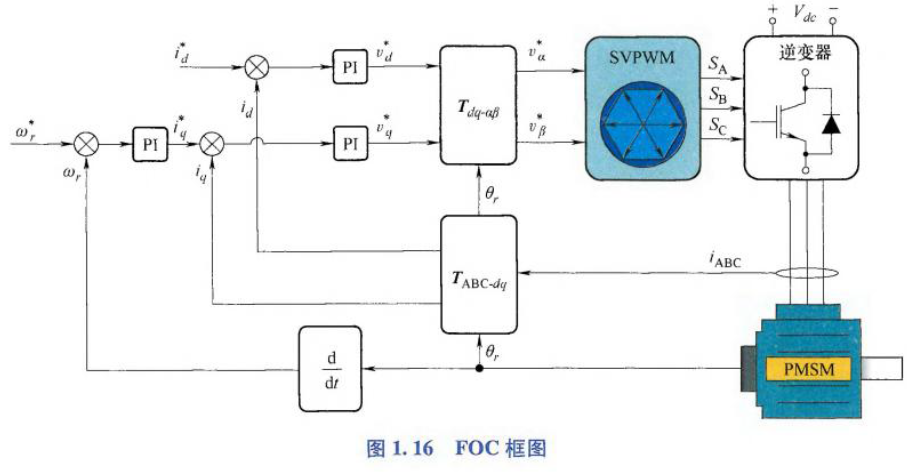
用于PMSM速度控制的FOC框图如下：
q轴电流 <=> 转矩，d轴电流 <=> 磁链，两者可独立调节

根据电流控制器输出的定子电压参考值，通过SVPWM进行调制，最终逆变器输出电压作用于电机.

直接转矩控制 DTC

直接转矩控制（DTC），结构简单、动态响应出色，对转子参数有良好鲁棒性. DTC基本原理：
1）根据定子电流、电压估算磁链和磁链转矩；
2）在基于开关表的传统DTC策略中，通常采用滞环控制器来调节电磁转矩和定子磁链；

步骤2）对应的直接转矩控制框图：

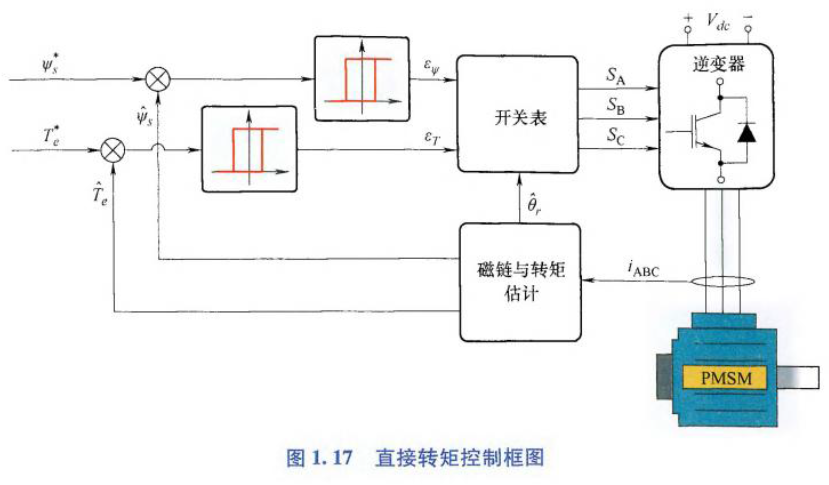
下面DTC开关表，列出了不同转子位置下\(ϵ_T,ϵ_e\)的电压矢量、相应的逆变器开关状态：

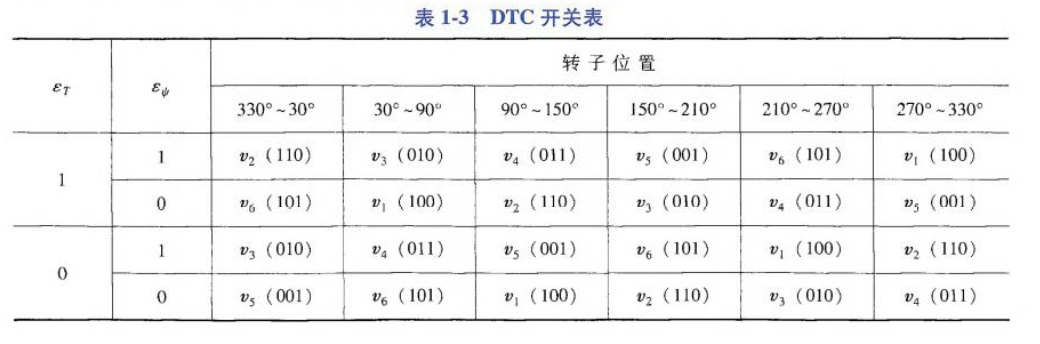
其中\(ϵ_T,ϵ_e\)分别为滞环控制器输出的转矩、磁链控制误差

DTC vs FOC：DTC无需坐标变换、特定的调制策略，因此动态转矩的控制性能得到显著提高.

数字控制器中，为减少纹波，可在DTC中使用SVPWM，采用固定的开关频率.

模型预测控制

模型预测控制主要包括：模型预测电流控制、模型预测转矩控制、模型预测速度控制.

模型预测电流控制框图：

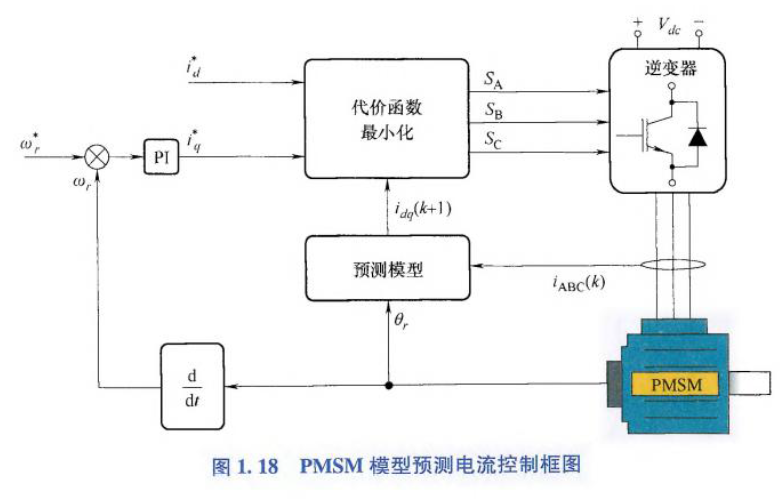
什么是模型预测电流控制？

首先，基于电机的数学模型和k时刻的采样电流，即\(i_{dq}(k)\)，以不同的逆变器开关状态迭代来预测在k+1时刻的采样电流，即\(i_{dq}(k+1)\).

根据电机的数学模型，电流的预测模型：

\[\begin{bmatrix}i_d^p(k+1)\\i_q^p(k+1)\end{bmatrix} =\begin{bmatrix} 1-\frac{T_s}{L_s}R_s & ω_rT_s\\ -ωT_s & 1-\frac{T_s}{L_s}R_s \end{bmatrix} \cdot \begin{bmatrix} i_d(k)\\i_q(k) \end{bmatrix} +\begin{bmatrix} \frac{T_s}{L_s} & 0\\ 0 & \frac{T_s}{L_s} \end{bmatrix} \cdot \begin{bmatrix}v_d(k)\\v_q(k)\end{bmatrix} + \begin{bmatrix}0\\-\frac{T_s}{L_s}ω_rψ_m\end{bmatrix} \]

其中，\(T_s\)采样周期

然后，构造代价函数，计算参考电流、预测电流之间的误差，令误差最小的电压矢量为最优的开关状态，被用于下一个开关周期：

\[g=|i_d^*-i_d^p(k+1)|+|i_q^*-i_q^p(k+1)| \]

MPC（微处理器）用预测值来确定开关状态，避免使用PWM，具有很好的动态性能. MPC主要问题：因模型不确定性导致的电流控制误差，需要进行额外的补偿；寻优过程可能需要大量计算，比较复杂、繁琐、耗时.

永磁无刷直流电机驱动的基本原理

数学模型

BLDC驱动系统采用与BLAC相同假设：

• 定子绕组在空间上对称分布，从而产生正弦电枢反应磁动势
• 转子上的永磁体在定子绕组中感应产生的电动势为正弦
• 三相绕组为星形联结，无中性点引出
• 忽略电机铁芯的损耗、饱和效应
• 忽略温度、负载引起的参数变化

BLDC三相定子电压方程：

\[\begin{bmatrix}v_a\\v_b\\v_c\end{bmatrix} =\begin{bmatrix} R_s & 0 & 0\\ 0 & R_s & 0\\ 0 & 0 & R_s \end{bmatrix} \cdot \begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} +p\begin{bmatrix} L_{AA} & M_{AB} & M_{AC}\\ M_{BA} & L_{BB} & M_{BC}\\ M_{CA} & M_{CB} & L_{CC} \end{bmatrix} \cdot \begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} + \begin{bmatrix}e_a\\e_b\\e_c\end{bmatrix} \]

其中，\(e_a,e_b,e_c\)三相反电动势；\(L_{AA},L_{BB},L_{CC}\)为三相绕组自感，\(_{AB},M_{BA},M_{BC},M_{CB},M_{AC},M_{CA}\)为三相绕组互感；p微分算子，\(p=d/dt\)

对于BLDC电机，通常采用表贴式永磁体，假设电感不随转子位置变化而变化，且三相对称，则自感、互感可表示为：

\[\begin{cases} L_{AA}=L_{BB}=L_{CC}=L\\ M_{AB}=M_{BA}= M_{BC}=M_{CB}=M_{AC}=M_{CA}=M \end{cases} \]

∴BLDC三相定子电压方程可写为：

\[\begin{bmatrix}v_a\\v_b\\v_c\end{bmatrix} =\begin{bmatrix} R_s & 0 & 0\\ 0 & R_s & 0\\ 0 & 0 & R_s \end{bmatrix} \cdot \begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} +\begin{bmatrix} L & M &M\\ M & L & M\\ M & M & L \end{bmatrix} \cdot p\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} + \begin{bmatrix}e_a\\e_b\\e_c\end{bmatrix} \]

可进一步化简为：

\[\begin{bmatrix}v_a\\v_b\\v_c\end{bmatrix} =\begin{bmatrix} R_s & 0 & 0\\ 0 & R_s & 0\\ 0 & 0 & R_s \end{bmatrix} \cdot \begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} +\begin{bmatrix} L-M & 0 & 0\\ 0 & L-M & 0\\ 0 & 0 & L-M \end{bmatrix} \cdot p\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} + \begin{bmatrix}e_a\\e_b\\e_c\end{bmatrix} \]

证明过程：

\[\begin{bmatrix} L & M &M\\ M & L & M\\ M & M & L \end{bmatrix} \cdot p\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} =\begin{bmatrix} L\frac{di_a}{dt}+M\frac{di_b}{dt}+M\frac{di_c}{dt}\\ M\frac{di_a}{dt}+L\frac{di_b}{dt}+M\frac{di_c}{dt}\\ M\frac{di_a}{dt}+M\frac{di_b}{dt}+L\frac{di_c}{dt} \end{bmatrix} \]

由基尔霍夫电流定律，\(i_c=-i_a-i_b\)
以A相感应电动势为例，对应矩阵第一行，

\[\begin{aligned} L\frac{di_a}{dt}+M\frac{di_b}{dt}+M\frac{di_c}{dt} &= L\frac{di_a}{dt}+M\frac{di_b}{dt}+M\frac{d(-i_a-i_b)}{dt}\\ &=(L-M)\frac{di_a}{dt} \end{aligned} \]

同理，B、C相可得感应电动势：

\[\begin{cases} B相\to (L-M)\frac{di_b}{dt}\\ C相\to (L-M)\frac{di_c}{dt} \end{cases} \]

于是，

\[\begin{aligned} \begin{bmatrix} L & M &M\\ M & L & M\\ M & M & L \end{bmatrix} \cdot p\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} &= \begin{bmatrix} L\frac{di_a}{dt}+M\frac{di_b}{dt}+M\frac{di_c}{dt}\\ M\frac{di_a}{dt}+L\frac{di_b}{dt}+M\frac{di_c}{dt}\\ M\frac{di_a}{dt}+M\frac{di_b}{dt}+L\frac{di_c}{dt} \end{bmatrix}\\ &=\begin{bmatrix} (L-M)\frac{di_a}{dt} & 0 & 0\\ 0 & (L-M)\frac{di_b}{dt} & 0\\ 0 & 0 & (L-M)\frac{di_c}{dt} \end{bmatrix}\\ &=\begin{bmatrix} L-M & 0 & 0\\ 0 & L-M & 0\\ 0 & 0 & L-M \end{bmatrix} \cdot p\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} \end{aligned} \]

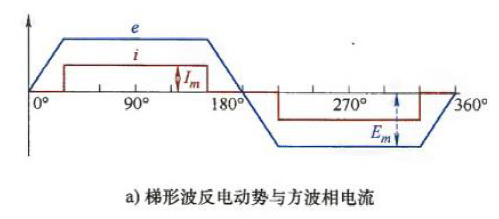
理想情况下，三相反电动势呈梯形：

控制策略

BLDC运行模式下，相电流应与反电动势保持同相位，使得定子磁链与转子磁链夹角保持60°~120°，从而最大化转矩输出. 通常，采用两相120°导通六步控制，如下图：

相电流在同相反电动势波形过零点30°后导通

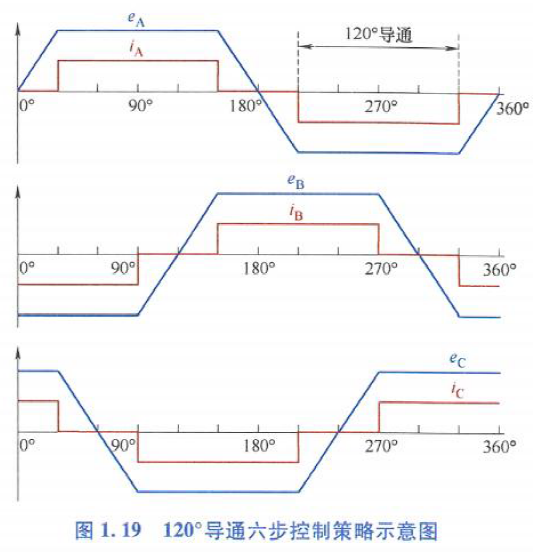
在两相120°导通六步控制中，一个基波周期被分为，每个扇区中，三相中2相导通，第三相悬浮. 每个相导通120°，然后关断60°. 在60°悬浮状态下，可以预测其反电动势，从而检测转子位置.

基波指在复杂的周期性振荡中与该振荡最长周期相等的正弦波分量，其频率称为基波频率，是信号分解中的最低频率成分.

120°导通的六步控制BLDC运行框图：
\(ω_r\)电机转速，\(i_{dc}\)直流母线电流，上标“*”参考值

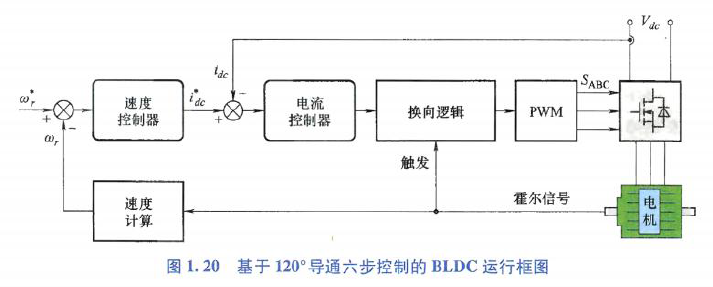
如下表，可根据转子位置定义6个扇区，扇区决定了三相导通模式，即上图的换向逻辑：

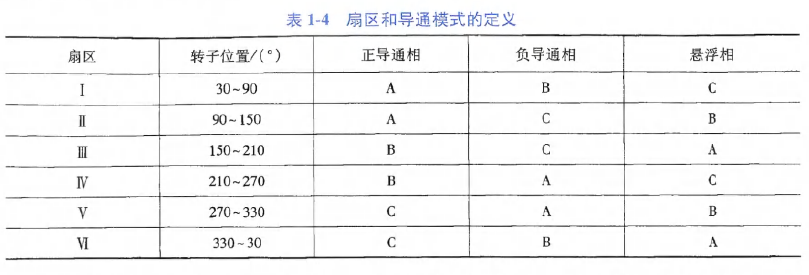
标准的120°导通六步控制系统，包括2个控制环路：用于速度控制的外环控制环路；用于电流控制的内环控制环路. 这2个控制环路级联连接.

因为电器变量（电阻、电感）的时间常数远低于机械变量的时间常数，所以内环比外环更快，电流控制器、速度控制器之间不会相互干扰，可独立设计、调整参数.

永磁无刷直流电机 vs 永磁无刷交流电机驱动

BLDC和BLAC运行模式比较：

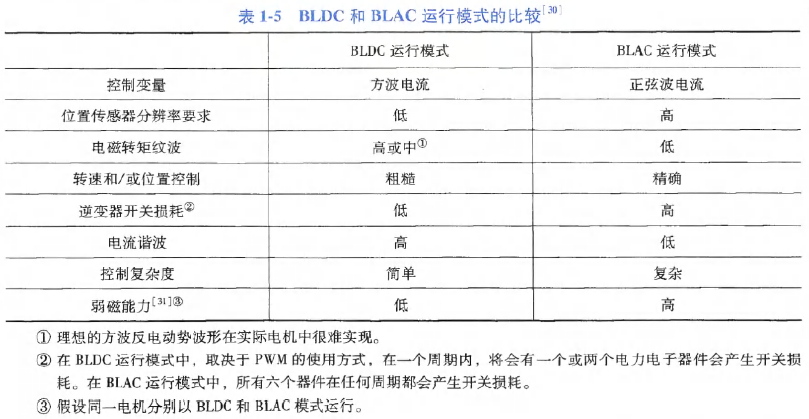
实际应用中，反电动势可能与理想波形有很大差异. 选择BLDC or BLAC运行模式，取决于具体应用，应该考虑各种因素，如实现复杂性、系统成本、性能需求等.

方波反电动势电机

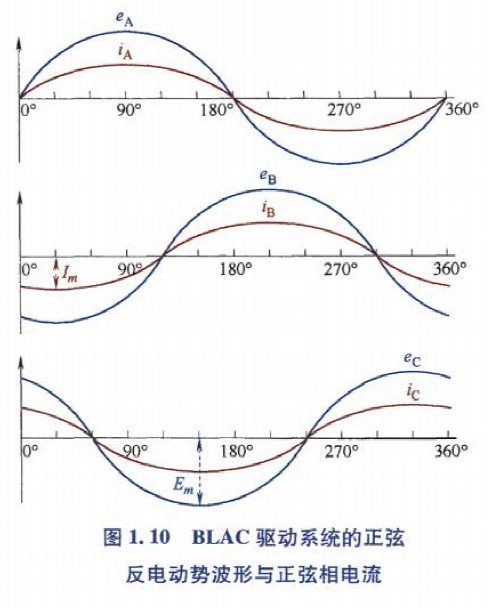
理想情况，具有方波反电动势的电机应该在BLDC模式下运行. 如下图，当相电流、反电动势都是理想波形，即反电动势为梯形波、平顶宽度120°电角度，同时电流为方波，那么BLDC电机的电磁转矩没有纹波，可表示为：

\[T_{m\_BLDC}=\frac{2E_mI_m}{ω_m} \]

其中，\(ω_m\)机械角速度

如下表，相电流、反电动势都包含丰富的谐波，相同阶次的电流、反电动势谐波之间的相互作用将产生有效电磁转矩：

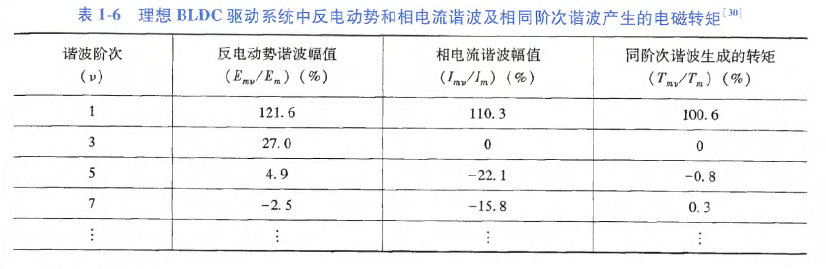
可看出：
1）相电流无3次谐波，但高阶谐波很显著；
2）相反电动势中最显著的谐波是3次谐波，而高次谐波相对较小. 不过3次谐波反电动势对电磁转矩无贡献，所以反电动势中只有基波分量占主导地位；
3）有效电磁转矩主要由基波反电动势、基波电流之间的相互作用产生，高阶谐波产生的有效电磁转矩很小；

实际应用在，方波反电动势电机也能在BLAC模式下运行，性能比较：

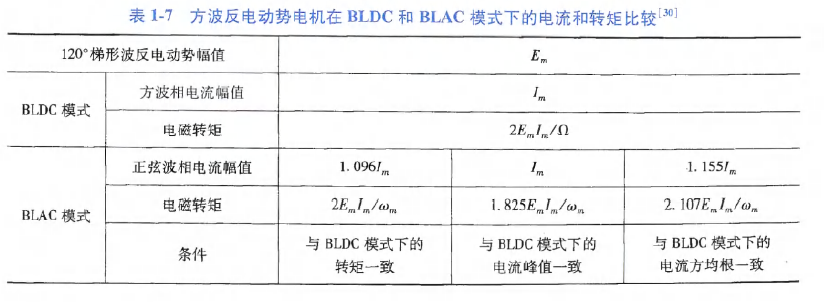
正弦波反电动势电机

理想情况，正弦波反电动势电机应以BLAC模式运行. 如下图，当相电流、反电动势都为理想的正弦波形时，电磁转矩无纹波，可表示为：

\[T_{m\_BLAC}=\frac{3E_mI_m}{2ω_m} \]

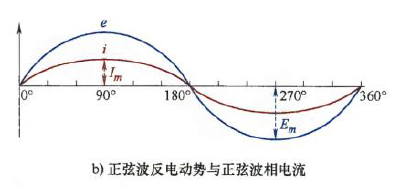
实际应用中，相电流无3次谐波，高次谐波通常较低，因此也可在BLDC模式下运行. 因此，电流基波分量占主导地位. 性能比较：

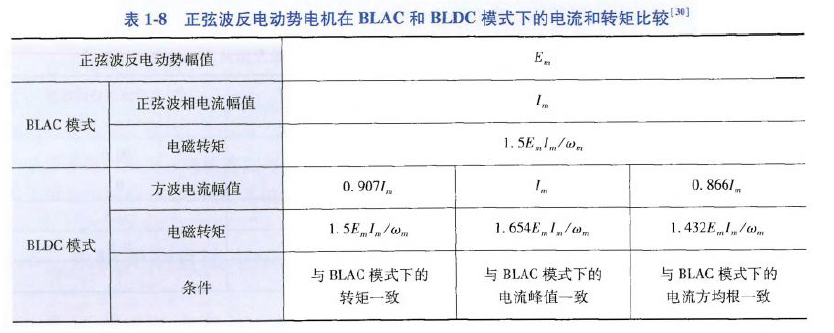
如果方波反电动势电机以BLAC模式运行，或正弦波反电动势电机以BLDC模式运行，或者电机反电动势波形既不是纯正弦波，也不是纯方波，或具有120°平顶的梯形波，则会产生转矩纹波.

无位置传感器控制技术及其应用

高性能永磁电机驱动系统需要转子位置信息，转子位置信息通常通过转子位置传感器进行测量而获得，例如旋转转变压器、编码器、霍尔传感器等.
不过，传感器会增大系统体积，尤其恶劣环境下，将降低系统可靠性. 所以，使用无位置传感器技术也是一种理想选择.

分类

基于BLAC、BLDC驱动系统的无位置传感器控制技术分类：

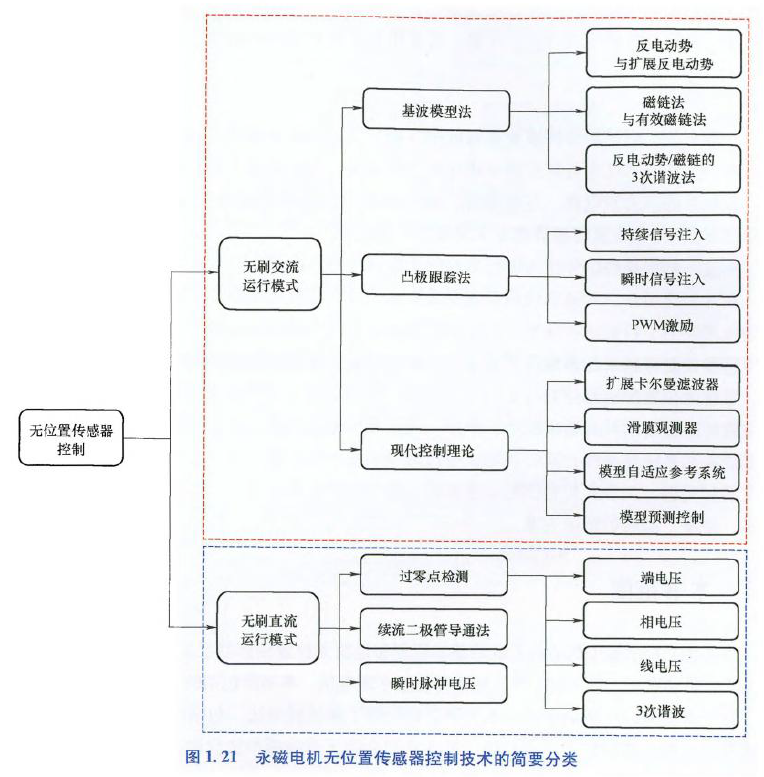
• BLAC模式下

1）基波模型法

利用反电动势或磁链，这种方法需要准确的电机参数、可观测的电机模型，它们更适合应用于中高速范围内.
对于SPM电机，可利用反电动势法、磁链法；
对于IPM电机，需要利用扩展反电动势法、有效磁链法实现无位置传感器控制.
除基波分量外，反电动势和磁链的3次谐波也能用于位置估计.

2）凸极跟踪法

对于基于转子凸极性，永磁电机的凸极性与转子速度无关. 通过不同信号注入方法，可用于零速、低速范围.

3）现代控制理论

扩展卡尔曼滤波器（EKF），滑膜观测器（SMO），模型参考自适应系统（MRAS）等，也可用于传统无位置传感器技术，提高位置估计性能.

• BLDC模式下

1）过零点检测（Zero-Cross Point，ZCP）应用广泛，依赖于反电动势幅值大小，仅在高速运行时性能量化
2）续流二极管导通法，间接检测ZCP
3）脉冲电压注入，可用于检测领转速时转子位置

应用

无位置传感器控制技术，适用于：启动转矩要求低的应用，如风扇、泵、吸尘器、干手机、吹风机、风力风电机等；
挑战：需要大转矩、频繁启动的应用，如工业驱动器、电动汽车

参考

[1] 诸自强, 吴溪蒙. 永磁同步电机无位置传感器控制[M]. 机械工业出版社,2025

[2] PMSM驱动控制学习(基础概念)---表贴式PMSM和内置式PMSM