数学基础：三角形重心坐标插值公式的证明

目录

• 线性坐标插值
• 三角形重心坐标插值
• 推广到n凸多边形

在快速Phong明暗处理（Blinn-Phong明暗处理）时，出现了三角形重心坐标插值公式，但没有给出证明. 网上也鲜有证明过程或较为复杂，这里给出简洁证明.

问题描述：在\(△ABC\)中，三顶点坐标\(A(x_1,y_1,z_1)、B(x_2,y_2,z_2)、C(x_3,y_3,z_3)\). 则三角形内任一点\(P(x,y,z)\)可表示为：

\[\tag{1} P=α A + β B + γ C, α + β + γ=1 \]

如何证明？
初看无从下手，可先考虑2个点的情况，即线性坐标插值.

线性坐标插值

如图，如果点\(P(x,y)\)为线段AB上一点，P点与A、B坐标关系怎样？

\[\bm{P}=u\bm{A}+(1-u)\bm{B}, 0\le u \le 1 \]

证明：
设坐标\(A(x_1,y_1)、B(x_2,y_2)\)
∵P在线段AB上
∴\(\overrightarrow{AP}\parallel \overrightarrow{BP}\)
即存在实数\(\lambda(\lambda\neq 0)\)，使得\((x-x_1,y-y_1)=\lambda(x-x_2,y-y_2)\)

∴

\[\begin{cases} x-x_1=\lambda(x-x_2) \\ y-y_1=\lambda(y-y_2) \end{cases} \]

有

\[x=\frac{1}{1-\lambda}x_1+(1-\frac{1}{1-\lambda})x_2 \]

令\(u=\frac{1}{1-\lambda}(\lambda\neq 1)\)，则\(x=ux_1+(1-u)x_2\)

同理，\(y=uy_1+(1-u)y_2\)
将2个等式合并成，写成向量形式：

\[\bm{P}=u\bm{A}+(1-u)\bm{B} \]

这里\(\bm{P},\bm{A},\bm{B}\)代表它们的笛卡尔坐标.

当\(\lambda=1\)时呢？
此时，由平行向量得到的等式与x、y无关，且要求A、B中点必须为原点，这没有意义.

如何求u范围？
不妨设\(x_1\le x_2\).
∵x位于线段AB（含端点）
∴\(x_1\le x \le x_2\)
∴\(x_1\le x=ux_1+(1-u)x_2\le x_2\)
∴

\[\begin{cases} (1-u)x_1\le (1-u)x_2 & (1)\\ ux_1\le ux_2 & (2) \end{cases} \]

如果\(u>1\)，则(1)与假设矛盾，故\(u\le 1\)；
如果\(u<0\)，则(2)与假设矛盾，故\(0\le u\).

综上，\(\bm{P}=u\bm{A}+(1-u)\bm{B}, 0\le u \le 1\)成立.

tips：该公式在Liang-Barsky线段裁剪算法中也有应用.

• u值是多少？如何求？

由于\(u=\frac{1}{1-\lambda}\)，因此求出\(\lambda\)即可.

\[\overrightarrow{AP}=\lambda\overrightarrow{BP}\implies |AP|=-\lambda |BP|\\ \therefore \lambda=-\frac{|AP|}{|BP|} \]

可得，

\[u=\frac{1}{1-\lambda}=\frac{1}{1+\frac{|AP|}{|BP|}}=\frac{|BP|}{|BP|+|AP|}=\frac{|BP|}{|AB|} \]

因此，线性坐标插值公式也可写为：

\[\bm{P}=u\bm{A}+(1-u)\bm{B}, u=\frac{|BP|}{|AB|} \]

或者，

\[\bm{P}=(1-λ)\bm{A}+λ\bm{B}, λ=\frac{|AP|}{|AB|} \]

三角形重心坐标插值

P是\(△ABC\)内任一点，连接CP交AB与G.
只要P在三角形内部而不是外部，则Q必位于线段AB上，而不是延长线上.

如此，可通过线段插值，分2步求P坐标与三角形关系：
（1）求Q坐标；（2）求P坐标.

∵Q是线段AB上一点

∴\(\exist u_1\)满足\(\bm{Q}=u_1\bm{A}+(1-u_1)\bm{B},0\le u_1 \le 1\)

∵P是线段CQ上一点

∴\(\exist u_2\)满足\(\bm{P}=u_2\bm{Q}+(1-u_2)\bm{C}, 0\le u_2 \le 1\)

∴联立2个等式，可得\(\bm{P}=u_1u_2\bm{A}+u_2(1-u_1)\bm{B}+(1-u_2)\bm{C}\)

又\(u_1u_2+u_2(1-u_1)+(1-u_2)=1\)
因此，令\(α=u_1u_2, β=u_2(1-u_1), γ=1-u_2, 0\le α,β,γ\le 1\)

P与A、B、C关系，可写成

\[\bm{P}=α\bm{A} + β\bm{B} + γ\bm{C}, α+β+γ=1且0\le α,β,γ \le 1 \]

关于\(α,β,γ\)详细求解过程，可参见：计算机图形：三角形及重心空间

推广到n凸多边形

推广：对于四边形，甚至n凸多边形，是否有同样的结论？

即n凸多边形\(A_1A_2...A_n\)内一点P，坐标与顶点是否有这样的关系\(\bm{P}=k_1\bm{A_1}+k_2\bm{A_2}+...+k_n\bm{A_n}，且k_1+k_2+...+k_n=1成立\)？
答案是肯定的. 数学归纳法证明.

证明：
1）当n=3时，问题简化为三角形插值，显然\(\bm{P_3}=k_1\bm{A_1}+k_2\bm{A_2}+k_3\bm{A_3}，k_1+k_2+k_3=1\)成立.

2）当n=m时，假设\(\bm{P_m}=k_1\bm{A_1}+k_2\bm{A_2}+...+k_m\bm{A_m}，k_1+k_2+...+k_m=1\)成立

那么，当n=m+1时，连接点\(A_{m+1}\)与点\(P_{m+1}\)
由于\(P_{m+1}\)在m+1凸多边形内部，因此\(A_{m+1}P_{m+1}\)与凸多边形必有2个交点（否则就不是凸多边形），而其中一个已经是顶点\(A_{m+1}\)，因此，另一个交点必然位于子凸多边形\(A_1A_2...A_{m}\)内

而m凸多边形\(A_1A_2...A_{m}\)内任一点，是可以用\(P_m\)表达式来表示的.

不妨直接取线段另一点为\(P_m\)，有\(P_{m+1}\)为线段\(P_mA_{m+1}\)上一点

∴\(\bm{P_{m+1}}=u\bm{P_m}+(1-u)\bm{A_{m+1}}\)
∴\(\bm{P_{m+1}}=uk_1\bm{A_1}+uk_2\bm{A_2}+...+uk_m\bm{A_m}+(1-u)\bm{A_{m+1}}\)

显然，系数和\(uk_1+uk_2+...+uk_m+(1-u)=1\)
令\(k_i'=uk_i(i=1,2,...,m)，k_i'=1-u(i=m+1)\)

则\(\bm{P_{m+1}}\)可写成\(\bm{P_{m+1}}=k_1'\bm{A_1}+k_2'\bm{A_2}+...+k_m\bm{A_m} + k_{m+1}\bm{A_{m+1}}\)
将\(k_i'\)写成\(k_i\)形式，则\(\bm{P_{m+1}}=k_1\bm{A_1}+k_2\bm{A_2}+...+k_{m+1}\bm{A_{m+1}}\)且\(k_1+k_2+...+k_{m+1}=1\)也成立

故得证.

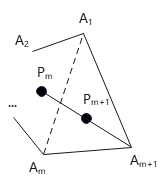
注：只要\(A_{m+1}\)与\(P_{m+1}\)连线的延长线经过前m个点形成的多边形区域即可，就能利用m多边形的插值公式+线段插值，求出\(P_{m+1}\)坐标.