电路基础：交流电路

目录

• 交流电路
  • 电磁感应定律
  • 交流发电机
  • 交流波形的描述
  • 交流电阻、电压、电流的有效值
• 参考

交流电路

电磁感应定律

运动的导体切割磁感线时，会产生感应电动势（楞次定律）.

而法拉第电磁感应定律指出，

任何封闭电路中感应电动势大小，等于穿过这一电路磁通量的变化率.

用公式表示：

\[E=-\frac{d\phi_B}{dt} \]

其中，

• \(E\)，感应电动势，单位V；
• \(\phi_B\)，通过电路的磁通量，单位韦伯；
• \(t\)，是时间，单位s

电动势的方向（公式中负号）由楞次定律提供.

楞次定律感应电流的方向，符合右手定则：伸出右手，使拇指与其他四个手指垂直，并且都处于同一平面内.

由磁通量定义，

\[\phi_B=BAcos θ \]

其中，\(θ\)是线圈法向量与磁场的夹角，A是线圈面积，\(Acos θ\)是切割磁感线的有效面积.

假设初始时，线圈与磁场方向垂直时，\(θ=π\to cos θ=-1\)；
当线圈与磁场方向平行时，\(θ=π/2\to cos θ=0\)

注意：磁场方向，在外部N->S，在内部S->N.

• 对于一扎线圈（线圈圈数N）

\[E=-N\frac{d\phi_B}{dt} \]

其中，\(\phi_B\)为通过一圈的磁通量

• 对于线圈绕绕旋转，角频率ω

\[∵θ=ωt\\ \begin{aligned} ∴E &= -N\frac{d\phi_B}{dt}\\ &= -N\frac{d(BAcos θ)}{dt}\\ &= -NBA\frac{d(cos ωt)}{dt}\\ &= NBAωsin ωt \end{aligned} \]

注意：\(cos' ax=-a\cdot sinax\)

当\(θ=ωt=π/2\)时，线圈//磁感线，此时感应电动势最大\(E_{max}=NBAω\)

交流发电机

下图是一个简单发电机示意图，发电机由磁体、线圈组成. 线圈放在N、S极之间，可以绕轴旋转. 线圈旋转时，通过线圈的磁通量不断改变，线圈中电荷受到磁场力而运动，从而在线圈两端形成感应电动势.

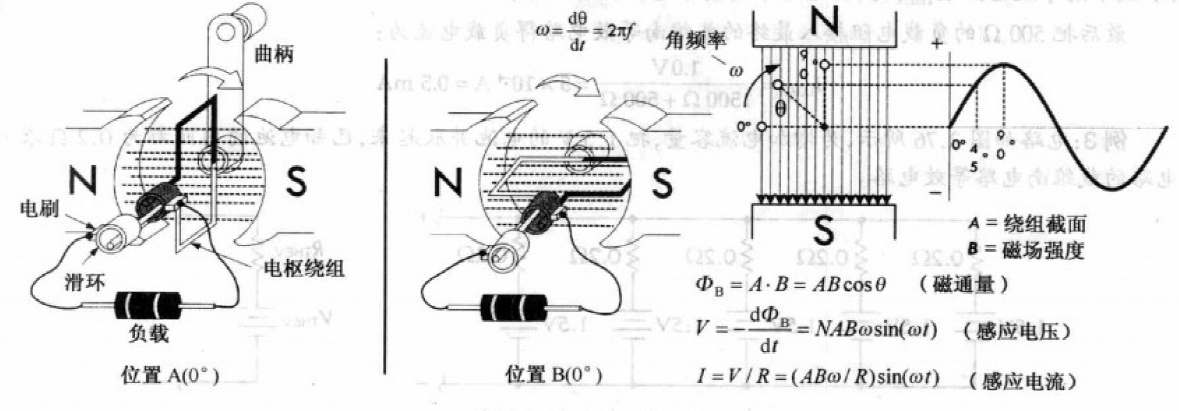
感应电压，公式推导，见上面 电磁感应定律.

由公式可知，感应电压是ω（rad/s）的正弦函数. ω与频率关系：

\[ω=\frac{dθ}{dt}=2πf \]

交流波形的描述

描述交流电压、电流，包括3个方面：幅值、频率、相位.

• 幅值

幅值的定义：一个周期的变化过程中，电压所能达到的最大值，称为电压的幅值.

如下图，是一个正弦电压与一个逆时针旋转360°圆周上相应的位置间的关系.
交流电压\(V(t)=V_psin(2πft+0°), f=1/T\)

横坐标是旋转角度（逆时针），纵坐标最大值就是幅值.

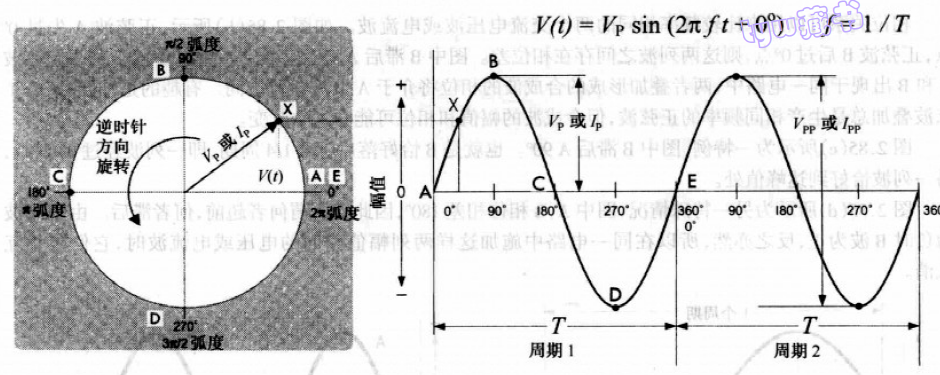
• 频率

持续旋转的发电机，产生正弦变化的电压，随着时间延续，正弦波不断循环. 在一个循环内任取一点，如峰值点，那么每秒内电压值达到峰值点的次数称为交变电流的频率f（转/秒，或Hz）.

每次循环所需时间，称为周期T

\[T=\frac{1}{f} \]

• 相位

由于旋转角度\(θ=ωt\)，所以交流感应电压也可以是时间t的正弦函数.

当我们画电压曲线时，横轴时间t，纵轴为电压值. 时间轴右侧，表示事件更晚发生，左侧更早发生.

虽然时间单位是秒，但是将波的一个循环周期分为360°，作为单位会更简便.

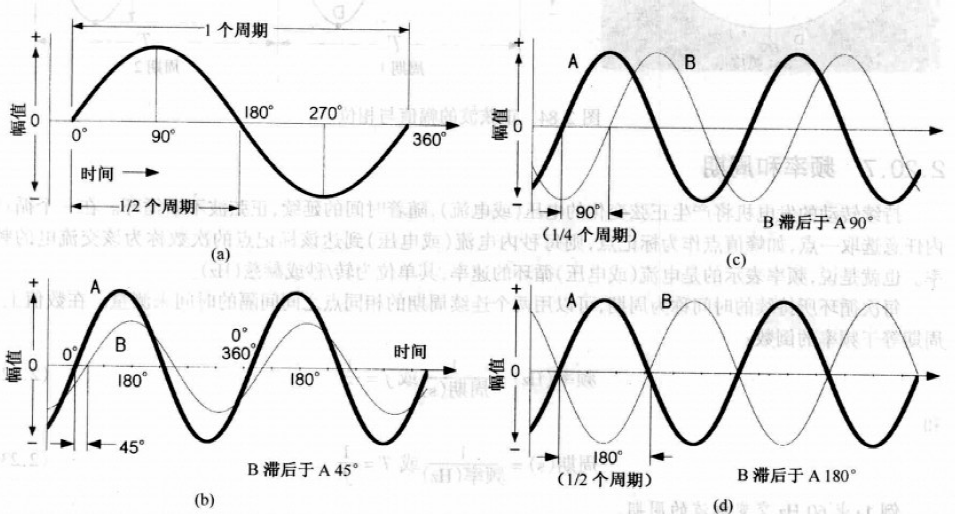
习惯上，常以0°作为计时起点，即电压或电流正半周（1/2周期）的起始点，如下图(a).

该方式表示交流电的周期，可使得计算与测量值的记录与频率无关. 一个周期内，电压正峰值出现在90°处，相对于0°起点，交流电峰值所处相位为90°.

相位有什么用？

可用来表示频率相同的2个交流电压. 如下图(b)，A超前B 40°，即A与B相位差为40°.

对于(c)，A、B相位差90°，即1/4周期. A到0点时，B刚好到峰值.

对于(d)，A、B相位差180°，即1/2周期. 同一时刻，电压值刚好相反. 无所谓超前、滞后.

叠加波：

两者叠加的波位于A、B波相位之间. 同频率波叠加，频率不变，但幅值和相位可能改变.

交流电阻、电压、电流的有效值

前面，我们假设线圈两端接入的是纯电阻，因此交流电压、电阻、电流符合欧姆定律.

\[\begin{aligned} V(t) &= V_psin(2πft)\\ I(t) &= \frac{V(t)}{R}=\frac{V_p}{R}sin(2πft) \end{aligned} \]

但是，实际应用中，我们接入的负载通常不是纯电阻（如接入电容、电感），那么就不能简单应用欧姆定律.

为求出正弦电压情况下电阻所消耗功率，可以应用欧姆定律，得到瞬时功率：

\[P(t)=\frac{V(t)^2}{R}=\frac{V_p^2}{R}sin^2(2πft)\\ =\frac{V_p^2}{2R}(1-cos (4πft)) \]

注意：\(sin^2x=\frac{1}{2}(1-cos 2x)\)

如何求一个周期内的发电机的功率？

一个周期内正、负波形相互抵消，平均值是0，如果用\(P=VI\)，那么功率是0. 这显然不正确，因为功率无方向，对于正半波和负半波，都传递能量.

我们使用RMS或均方根值，来替换电流或电压来求平均.

RMS：通过对交变电压或电流的瞬间值进行平方，然后取其一个周期内的平均值（积分->平均），再对平均值开平方根，从而求得RMS.

RMS是一个不为0的值，称为有效值.

设正弦交流电压、电流：\(V(t)=V_psin(2πft),I(t)=I_psin(2πft)\)，那么正弦电压、电流的RMS值：

\[\begin{aligned} V_{RMS}&=\sqrt{\frac{1}{T}\int_0^T V(t)^2dt}=\frac{1}{\sqrt 2}V_p=0.707V_p, RMS电压\\ I_{RMS}&=\sqrt{\frac{1}{T}\int_0^T I(t)^2dt}=\frac{1}{\sqrt 2}I_p=0.707I_p, RMS电流 \end{aligned} \]

下面只证明 RMS电压：

\[\begin{aligned} V_{RMS}&=\sqrt{\frac{1}{T}\int_0^TV(t)^2dt}\\ &=\sqrt{\frac{1}{T}\int_0^T \biggm[V_psin(2πft)\biggm]^2dt}\\ &=V_p\sqrt{\frac{1}{2T}\int_0^T \biggm[1-cos(4πft)\biggm]dt}\\ &=V_p\sqrt{\frac{1}{2T}\biggm[\int_0^T dt - \int_0^T cos(4πft)dt\biggm]}\\ &=V_p\sqrt{\frac{1}{2T}\biggm[T-\int_0^{4πfT} cos(4πft)d(4πft)\biggm]}\\ &=V_p\sqrt{\frac{1}{2T}\biggm[ T-sin(4πft)\biggm\vert_{0}^{4πfT}}\biggm]\\ &=\frac{1}{\sqrt 2}V_p \end{aligned} \]

可以看出，电压、电流的RMS值只与峰值有关，与时间、频率无关.

平均交流功率：

\[P_{avg}=I_{RMS}\times V_{RMS}=\frac{1}{2}V_pI_p=\frac{P_{peak}}{2} \]

其中， \(P_{peak}\)是峰值功率.

将电压、电流RMS值，代入欧姆定律，得到交流欧姆定律：

\[V_{RMS}=I_{RMS}\times R \]

代入功率定理中，可得交流功率定理：

\[P_{RMS}=I_{RMS}\times V_{RMS}=\frac{V_{RMS}^2}{R}=I_{RMS}^2R \]

参考

[1] 美 舍茨 Scherz, Paul.实用电子元器件与电路基础[M].电子工业出版社,2009.

[2] https://zh.wikipedia.org/wiki/法拉第电磁感应定律

[3]https://baike.baidu.com/item/电磁感应/634847